圣彼得堡现象。概率论的悖论。 - 页 5 123456789101112...25 新评论 TheXpert 2018.10.24 11:41 #41 我认为研究博弈理论,如角斗士悖论,对赚钱更有帮助。 Violetta Novak 2018.10.24 12:09 #42 hartmann: 在这里,我已经做了计算。 100,000个游戏的数字是8.32卢布。 一百万次游戏,这个数字是25.76卢布。 游戏越多,数字越高。 这就像马丁格尔法:你玩的游戏越多,输的概率就越高。帮我看看这个帖子里的文件,我搞不清楚,D列的公式是=A(A1) Violetta Novak 2018.10.24 12:33 #43 Олег avtomat:数学谜题和乐趣这本由美国著名科学普及者M.Gardner撰写的书中有很多来自不同数学分支的非常有趣的问题和谜题。成功的材料选择、完全不同寻常的表现形式和作者微妙的幽默感将给广大读者带来极大的乐趣--希望有效地利用空闲时间的数学爱好者们。谢谢你,奥列格,令人印象深刻))。 Georgiy Merts 2018.10.24 12:35 #44 没错,加德纳就有这种游戏,在那里也是通过限制银行存款来解决悖论,之后投注数字就变得相当理智。 Alexey Navoykov 2018.10.24 13:02 #45 Maxim Kuznetsov:来得到一个0到6之间的随机数(7个中的一个)。 - 考虑limit=RAND_MAX - (RAND_MAX%7) ; 在0...RAND_MAX范围内7的最大倍数。 - 使用RDS,直到我们得到r<limit;也就是说,如果 "随机数 "高于limit,我们就不能用它做任何事情--我们采取 - 结果 = r % 7 或(无论好坏)r * 7 / limit 像这样的:-)可能是错误的+-1。在我们的例子中,RAND_MAX = 32767被7除以,没有余数,所以你的例子不是很好。 如果我们考虑一般情况,我们会得到有利于大于余数的概率倾斜。 也就是说,如果说RAND_MAX%7=4,我们更多的时候会得到5和6,这就是为什么没有东西应该被丢弃。一切都必须考虑到。 Renat Akhtyamov 2018.10.24 13:28 #46 hartmann: 在这里,我已经做了计算。 对于100,000场比赛,这个数字是8.32卢布。 对于一百万场比赛,这个数字是25.76卢布。 游戏越多,数字越高。 这就像马丁格尔法:你玩得越多,输的机会就越大。 如果你考虑一下呢? multiplicator 2018.10.24 13:43 #47 Novaja:游戏要点:进入游戏需要存款,投币游戏持续到第一只老鹰出现(一次性游戏),当第一轮出现老鹰时,1-doucat获胜,如果出现反面,第二轮出现老鹰时,获胜金额翻倍,以此类推,直到出现老鹰为止,无限期。赢取1杜卡的概率为0.5,2-0.25,4-0.125,等等。 因此,如果银行金额是无限的,就有可能赢得无限,玩得无限。 关于交易、自动交易系统和交易策略测试的论坛 圣彼得堡现象"。概率论的悖论。 Novaja, 2018.10.24 10:02 游戏的意义:进入游戏需要存款,投币游戏持续到第一只老鹰出现(一次性游戏),当老鹰出现在第一卷时,1倍赢,如果出现尾巴,老鹰出现在第二卷,赢的金额加倍,如此循环,直到老鹰出现。赢得1杜卡的概率-0.5,2-0.25,4-0.125等,所以你可以赢得无限,玩得无限,如果锅是无限的。 我也在做这样的图。你从哪里得到的? multiplicator 2018.10.24 13:45 #48 Novaja:帮我看看这个帖子的文件,我不明白D列,它的公式是=A(A1) 这是我自己写的一个函数,叫A()。 简而言之,它计算的是老鹰落在哪一滴。 multiplicator 2018.10.24 13:48 #49 Renat Akhtyamov: 如果你考虑一下呢? 不写无意义的帖子如何? Renat Akhtyamov 2018.10.24 13:50 #50 hartmann: 不写无意义的帖子如何? 你在这个帖子中犯了很大的错误 123456789101112...25 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
在这里,我已经做了计算。
100,000个游戏的数字是8.32卢布。
一百万次游戏,这个数字是25.76卢布。
游戏越多,数字越高。
这就像马丁格尔法:你玩的游戏越多,输的概率就越高。
帮我看看这个帖子里的文件,我搞不清楚,D列的公式是=A(A1)
数学谜题和乐趣
这本由美国著名科学普及者M.Gardner撰写的书中有很多来自不同数学分支的非常有趣的问题和谜题。成功的材料选择、完全不同寻常的表现形式和作者微妙的幽默感将给广大读者带来极大的乐趣--希望有效地利用空闲时间的数学爱好者们。
谢谢你,奥列格,令人印象深刻))。
来得到一个0到6之间的随机数(7个中的一个)。
- 考虑limit=RAND_MAX - (RAND_MAX%7) ; 在0...RAND_MAX范围内7的最大倍数。
- 使用RDS,直到我们得到r<limit;也就是说,如果 "随机数 "高于limit,我们就不能用它做任何事情--我们采取
- 结果 = r % 7 或(无论好坏)r * 7 / limit
像这样的:-)可能是错误的+-1。
在我们的例子中,RAND_MAX = 32767被7除以,没有余数,所以你的例子不是很好。 如果我们考虑一般情况,我们会得到有利于大于余数的概率倾斜。
也就是说,如果说RAND_MAX%7=4,我们更多的时候会得到5和6,这就是为什么没有东西应该被丢弃。一切都必须考虑到。
在这里,我已经做了计算。
对于100,000场比赛,这个数字是8.32卢布。
对于一百万场比赛,这个数字是25.76卢布。
游戏越多,数字越高。
这就像马丁格尔法:你玩得越多,输的机会就越大。
游戏要点:进入游戏需要存款,投币游戏持续到第一只老鹰出现(一次性游戏),当第一轮出现老鹰时,1-doucat获胜,如果出现反面,第二轮出现老鹰时,获胜金额翻倍,以此类推,直到出现老鹰为止,无限期。赢取1杜卡的概率为0.5,2-0.25,4-0.125,等等。 因此,如果银行金额是无限的,就有可能赢得无限,玩得无限。
关于交易、自动交易系统和交易策略测试的论坛
圣彼得堡现象"。概率论的悖论。
Novaja, 2018.10.24 10:02
游戏的意义:进入游戏需要存款,投币游戏持续到第一只老鹰出现(一次性游戏),当老鹰出现在第一卷时,1倍赢,如果出现尾巴,老鹰出现在第二卷,赢的金额加倍,如此循环,直到老鹰出现。赢得1杜卡的概率-0.5,2-0.25,4-0.125等,所以你可以赢得无限,玩得无限,如果锅是无限的。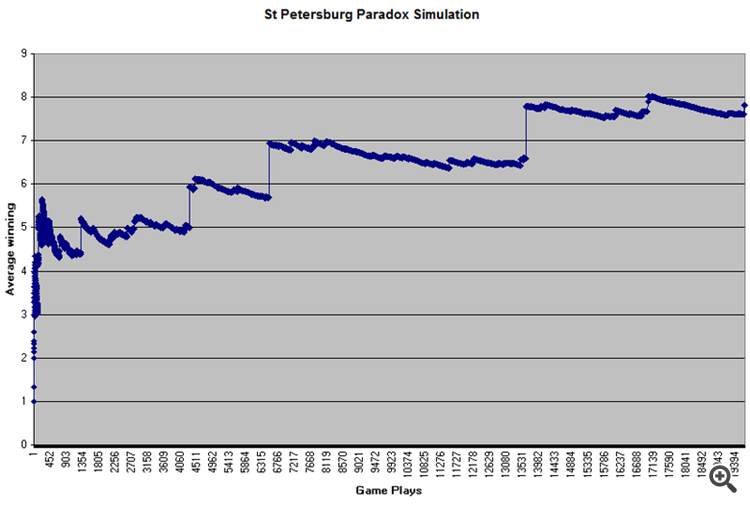
帮我看看这个帖子的文件,我不明白D列,它的公式是=A(A1)
简而言之,它计算的是老鹰落在哪一滴。
如果你考虑一下呢?
不写无意义的帖子如何?