joo
对于初学者,我认为你需要把代码带到。
1.可编撰。
2.可读的形式。
3.评论。
原则上说,这个话题很有意思,也很紧迫。
joo
对于初学者,我认为你需要把代码带到。
1.可编撰。
2.可读的形式。
3.评论。
好的。
我们有一个分类的实数数组。你需要在阵列中选择一个单元,其概率与假想轮盘区的大小相对应。
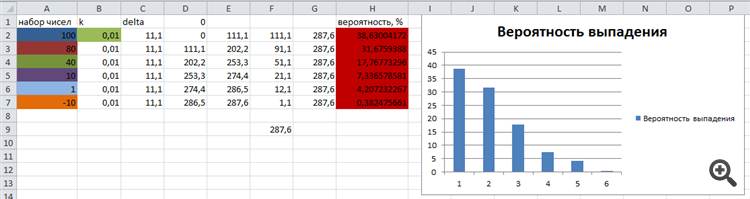
在Excel中计算了测试集的数字及其理论上的落空概率,并在下图中展示了与算法结果的对比。
运行该算法的结果。
2012.04.04 21:35:12 轮盘 (EURUSD,H1) h0 38618465 38.618465
2012.04.04 21:35:12 轮盘 (EURUSD,H1) h1 31685360 31.68536
2012.04.04 21:35:12 轮盘 (EURUSD,H1) h3 7.334754 7.334754
2012.04.04 21:35:12 轮盘 (EURUSD,H1) h4 4205492 4.205492
2012.04.04 21:35:12 轮盘 (EURUSD,H1) h5 385095 0.385095
2012.04.04 21:35:12 Roulette (EURUSD,H1) 12028 ms - 执行时间
正如你所看到的,"球 "落在相应扇区的概率结果与理论计算的结果几乎相同。
#property script_show_inputs //--- input parameters input int StartCount=100000000; // Границы соответствующих секторов рулетки double select1[]; // начало сектора double select2[]; // конец сектора //—————————————————————————————————————————————————————————————————————————————— void OnStart() { MathSrand((int)TimeLocal());// сброс генератора // массив с тестовым набором чисел double array[6]={100.0,80.0,40.0,10.0,1.0,-10.0}; ArrayResize(select1,6);ArrayInitialize(select1,0.0); ArrayResize(select2,6);ArrayInitialize(select2,0.0); // счетчики для подсчета выпадений соответствующего числа из тестового набора int h0=0,h1=0,h2=0,h3=0,h4=0,h5=0; // нажмём кнопочку секундомера int time_start=(int)GetTickCount(); // проведём серию испытаний for(int i=0;i<StartCount;i++) { switch(Roulette(array,6)) { case 0: h0++;break; case 1: h1++;break; case 2: h2++;break; case 3: h3++;break; case 4: h4++;break; default: h5++;break; } } Print((int)GetTickCount()-time_start," мс - Время исполнения"); Print("h5 ",h5, " ",h5*100.0/StartCount); Print("h4 ",h4, " ",h4*100.0/StartCount); Print("h3 ",h3, " ",h3*100.0/StartCount); Print("h1 ",h1, " ",h1*100.0/StartCount); Print("h0 ",h0, " ",h0*100.0/StartCount); Print("----------------"); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Рулетка. int Roulette(double &array[], int SizeOfPop) { int i=0,u=0; double p=0.0,start=0.0; double delta=(array[0]-array[SizeOfPop-1])*0.01-array[SizeOfPop-1]; //------------------------------------------------------------------------------ // зададим границы секторов for(i=0;i<SizeOfPop;i++) { select1[i]=start; select2[i]=start+MathAbs(array[i]+delta); start=select2[i]; } // бросим "шарик" p=RNDfromCI(select1[0],select2[SizeOfPop-1]); // посмотрим, на какой сектор упал "шарик" for(u=0;u<SizeOfPop;u++) if((select1[u]<=p && p<select2[u]) || p==select2[u]) break; //------------------------------------------------------------------------------ return(u); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Генератор случайных чисел из заданного интервала. double RNDfromCI(double min,double max) {return(min+((max-min)*MathRand()/32767.0));} //——————————————————————————————————————————————————————————————————————————————
好的。
我们有一个分类的实数数组。我们需要在阵列中选择一个单元,其概率与假想轮盘区的大小相对应。
解释一下设置 "扇形宽度 "的原理。 它是否与数组中的数值相对应?还是单独设置?
这是最黑暗的问题,其他的都不是问题。
第二个问题:0.01这个数字是什么? 它是从哪里来的?
简而言之:告诉我在哪里可以得到正确的扇形落差概率(宽度为圆周率的一部分)。
你可以只是每个扇区的大小。 只要(默认)自然界中不存在负的大小。 即使是在赌场中。;)
解释一下设置 "扇形宽度 "的原理。 它是否与数组中的数值相对应?还是单独设置?
扇区的宽度不能与数组中的数值相对应,否则该算法将无法对所有数字起作用。
重要的是这些数字之间的距离。所有的数字离第一个数字越远,它们就越不可能掉出来。在本质上,我们推迟在一条直线上的酒吧成比例的数字之间的距离,调整的因素为0.01,所以,最后一个数字的概率下降不等于0,因为从第一个最远的。系数越高,各部门就越平等。附上Excel文件,用它做实验。
MetaDriver。
1.简而言之:告诉我在哪里可以得到正确的区段辍学概率(宽度为圆周率的几分之一)。
2.你可以直接确定每个扇区的大小。假设(默认)自然界中不存在负数,甚至不存在赌场。;)1.理论概率的计算在EXCEL中给出。第一个数字是最高概率,最后一个数字是最低概率,但不等于0。
2)对于任何一个数字集合来说,扇形的负数都不存在,只要该集合按降序排序--第一个数字是最大的(对于该集合中最大的但为负数的数字也可以)。
扇形的宽度不能与数组中的数值相匹配,否则该算法将无法对所有数字起作用。
胡:重要的是数字之间的距离。所有数字与第一个数字的距离越远,它们就越不可能掉出来。实质上我们在一条直线上推迟了与数字之间的距离成正比的线段,并以0.01的系数进行调整,这样最后一个数字不掉队的概率是0,因为离第一个数字最远。系数越高,各部门就越平等。excel文件附在后面,用它来实验。
1.理论概率的计算在EXCEL中给出。第一个数字是最高概率,最后一个数字是最低概率,但不等于0。
2.任何一组数字都不会有负的扇形大小,只要这组数字按降序排序--第一个数字是最大的(对这组数字中最大的,但也是负数)。
你的计划 "突然 "设定了最小的 数字 的概率(vmh)。没有任何合理的 理由。
// 由于 "辩解 "有点困难。没关系--N个钉子之间只有N-1个空格。
所以,这取决于 "系数",也是从盒子里拿出来的。为什么是0.01? 为什么不是0.001?
在做算法之前,你需要决定所有 扇区的 "宽度 "的计算。
zyu:给出 "数字之间的距离 "的计算公式。哪 个数字是 "第一"?它与自己的距离是多少?不要把它送到Excel,我去过那里。这在意识形态层面上是令人困惑的。修正系数从何而来,为什么会这样?
红色的那个根本不是真的。:)
它将是非常快的。
int Selection() { return(RNDfromCI(1,SizeOfPop); }
整个算法的质量不应受到影响。
而且,即使是这样,这个选项也会以牺牲速度为代价超越质量。
1.你的计划 "突然 "设定了最小的 数字 的概率(vmh)。没有任何合理的 理由。所以它(vmh)取决于 "系数",也是 "开箱即用"。 为什么是0.01? 为什么不是0.001?
2.在做算法之前,你需要决定所有 扇区的 "宽度 "的计算。
3.祖:给出 "数字之间的距离 "的计算公式。 哪个数字是 "第一"?它离自己有多远?不要把它送到Excel,我去过那里。这在意识形态层面上是令人困惑的。修正系数到底从何而来,为什么?
4.红色标注的内容根本不是事实。:)
1.是的,这不是真的。我喜欢这个系数。如果你喜欢另一个,我就用另一个--算法的速度不会改变。
2.达到确定的程度。
3.好的,我们有一个分类的数字数组--array[],其中最大的数字在array[0]中,而数字射线的起点是0.0(你可以采取任何其他的点--什么都不会改变),并且指向正方向。以这种方式排列射线上的各段。
start0=0=0 end0=start0+|array[0]+delta|
start1=end0 end1=start1+|array[1]+delta||
start2=end1 end2=start2+|array[2]+delta||
......
start5=end4 end5=start5+|array[5]+delta||
在哪里?
delta=(array[0]-array[5])*0.01-array[5];
这就是所有的算术。:)
现在,如果我们在我们标记的射线上扔一个 "球",击中某一段的概率与该段的长度成正比。
4.因为你强调了错误的(不是全部)。你应该强调:"从本质上讲,我们是在数线上绘制与数字之间的距离成比例的线段,用0.01的系数进行修正,以便最后一个数字没有击中0的概率"。
它将是非常快的。
int Selection() { return(RNDfromCI(1,SizeOfPop); }
整个算法的质量不应受到影响。
而且,即使稍有影响,它也会以牺牲速度为代价,超越质量。
:)
你的意思是,你只是简单地随机选择一个数组元素 吗?- 这并没有考虑到数组数字之间的距离,所以你的选项是没有用的。

- www.mql5.com
实验证实它是没有价值的吗?
我建议在这里讨论最优算法逻辑的问题。
如果有人怀疑他们的算法在速度(或清晰度)方面有最佳的逻辑,那么欢迎他们。
另外,我欢迎那些想练习自己的算法和帮助别人的人来到这个主题。
最初我把问题贴在 "傻瓜的问题 "分支,但我意识到,它不属于那里。
因此,请建议一个比这个算法更快的 "轮盘 "变体。
显然,数组可以从函数中取出来,这样它们就不必每次都被声明并调整大小,但我需要一个更革命性的解决方案。:)