有趣的资料,谢谢!
我不喜欢模式识别的实施:
//+------------------------------------------------------------------+ //|| 模式识别| //+------------------------------------------------------------------+ PATTERN_TYPE CProgram::GetPatternType(double A,double B,double C,double D,double E)
很明显,这种方法完成了它的任务,也许对这篇文章来说,它是最佳解决方案。
我想找到一个更优雅(通用)的解决方案来解决这个问题,比如用矩阵来存储数据(数组)?- 有没有人遇到过这样的模式搜索 实现方法?
图片中的 M2 和 M4 图案是一样的,是打错了吗?
我们会改正的,谢谢。
有趣的东西,谢谢!
我不喜欢模式识别的实现:
很明显,这种方法完成了它的任务,也许对这篇文章来说,它是最佳解决方案
我想找到一种更优雅(通用)的解决方案来解决这个问题,比如用矩阵来存储数据(数组)?- 有没有人遇到过这样的模式搜索实现方法?
当然,我们可以把所有数据都放到一个结构或数组中。但到目前为止,从头开始理解多段线的点的形式还是比较容易的。
...
我想找到一个更优雅(通用)的解决方案来解决这个问题,比如用矩阵来存储数据(数组)?- 有人遇到过这样的模式搜索实现吗?
我遇到过,而且是通用的。但我不太可能找到,我甚至不知道从哪里开始找。
有一条线,有两个点。第三点可以占据两个位置中的一个:第一点和第二点之间,或者第一点之上(假设第一条直线的方向是向上的)。现在有三个点,第四个点可以占据三个位置中的一个,也可以占据两个.... 的底部。首先,数组中有两个点,你站在索引 1 处,将第三个点位置的所有变量加到数组的末尾。移动到索引 2,将另一个点的所有变体添加到数组末尾....。等等。只要数组的 大小达到指定的大小,模式本身就是由数字设定的--这里就是带有这个数字的模式。您需要一个结构数组,在结构数组中包含一个点号数组。
***
数组不包含点的坐标,而是从头开始的顶点编号。例如,M16 可以这样编码:{1, 3, 2, 5, 4}.如果再添加一个顶点,会得到这些选项吗?
{1, 3, 2, 5, 4}
{1, 3, 2, 5, 6, 4}
{1, 3, 2, 5, 4, 6}
***
下面是我们检查的方法。假设我们正在寻找一种模式:{1, 3, 2, 5, 4} 这意味着顶点 1 在 3 的下方,5 在 2 的上方和 4 的下方,等等。
是的,它很普遍。但我想我找不到了,我甚至不知道从哪里开始找。
有一条线,它是两个点。第三点可以占据两个位置中的一个:在第一点和第二点之间,或者在第一点之上(假设第一条线的方向是向上的)。现在有三个点,第四个点可以占据三个位置中的一个,也可以占据两个.... 的底部。首先,数组中有两个点,你站在索引 1 处,将第三个点位置的所有变量加到数组的末尾。移动到索引 2,将另一个点的所有变体添加到数组末尾....。等等。只要数组的大小达到指定的大小,模式本身就是由数字设定的--这里就是带有这个数字的模式。您需要一个结构数组,在结构数组中包含一个点号数组。
***
数组不包含点的坐标,而是从头开始的顶点编号。例如,M16 可以这样编码:{1, 3, 2, 5, 4}.如果再增加一个顶点,会得到这些变体吗?
{1, 3, 2, 5, 4}
{1, 3, 2, 5, 6, 4}
{1, 3, 2, 5, 4, 6}
***
检查的方法是这样的。假设我们正在寻找一种模式:{1, 3, 2, 5, 4} 这意味着顶点 1 在 3 的下方,5 在 2 的上方和 4 的下方,等等。
没错,这就是我想找到的编码。
它看起来像一个加权图邻接矩阵,其中的权重意味着哪个顶点比当前顶点高/低。
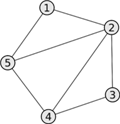
- neerc.ifmo.ru
当然,我们也可以将其全部放入一个结构或数组中。但这样更容易从头理解折线的点的形式。
显然,除了通用性,文章中的代码还应该清晰可读,但我喜欢组合问题,或者说喜欢动脑筋,所以我通过在 ME 中搜索,将这个函数按第一个条件分组:
//+------------------------------------------------------------------+ //|| 模式识别| //+------------------------------------------------------------------+ PATTERN_TYPE GetPatternType(double A,double B,double C,double D,double E) { if(A>B && C>A && B>E && E>D) return(W6); if(A>B && C>E && E>A && B>D) return(W11); if(A>B && E>C && C>A && B>D)return(W12); if(A>B && C>E && E>D && D>A)return(W15); if(A>B && E>C && C>D && D>A) return(W16); // A>C if(A>C && B>D && D>A && C>E) return(M3); if(A>C && B>D && D>E && E>A) return(M8); if(A>C && D>B && B>E && E>A) return(M10); if(A>C && C>B && B>E && E>D) return(W1); if(A>C && C>E && E>B && B>D) return(W2); if(A>C && C>E && E>D && D>B) return(W4); if(A>C && E>A && C>B && B>D) return(W8); if(A>C && E>A && C>D && D>B)return(W10); // C>A else ? if(C>A && B>D && D>C && A>E) return(M7); if(C>A && D>B && B>C && A>E) return(M9); if(C>A && B>D && D>E && E>C) return(M13); if(C>A && D>B && B>E && E>C) return(M15); if(C>A && D>E && E>B && B>C) return(M16); if(C>A && A>E && E>B && B>D) return(W7); if(C>A && A>E && E>D && D>B) return(W9); if(C>A && E>C && A>D && D>B) return(W14); if(B>A && A>D && D>C && C>E) return(M1); if(B>A && A>D && D>E && E>C) return(M2); if(B>A && D>B && A>C && C>E) return(M5); if(B>A && D>B && A>E && E>C) return(M6); if(B>A && D>E && E>B && A>C) return(M11); if(B>D && D>A && A>E && E>C) return(M4); if(B>D && D>C && C>E && E>A) return(M12); if(B>D && A>E && E>C && C>B) return(W3); if(D>B && B>C && C>E && E>A) return(M14); if(D>B && A>E && E>C && C>D) return(W5); if(D>B && C>E && E>A && A>D) return(W13); return(-1); }
应该还有一个紧凑而通用的解决方案!.....但我还没看到
显然,除了普遍性,文章中的代码还应该是可视的、可读的,但我喜欢关于组合学的问题,或者说喜欢动动脑子,所以我通过在 ME 中搜索,将这个函数按第一个条件分组:
.....但我还没看到
德米特里建议的解决方案不错。你可以这样做:
在 GetPatternType 方法的参数中传递模式维度,仅此而已。它本身会根据这个数字生成所有可能的组合,并根据这些数据在结构或数组中搜索给定的组合。
新文章 美林(Merrill)形态已发布:
在本文中,我们将研究美林形态的模型,并尝试评估它们与当前行情的相关性。 为此,我们将开发一种工具来测试形态,并将其模型应用在各种数据类型,例如收盘价、最高价和最低价,以及震荡指标。
为了阐明我们在应用美林形态时如何以及该使用哪些数据,我们需要了解它们的实际含义。 主要的两个类别是类似于字母 M 和 W 的图案。它们被称为 M 和 W 形态。 每个类别包含 16 种形态。
图例 1、示意 16 个 M 形态。 我们可以看到,区别在于构成形态的五个点的相互排列。
作者:Alexander Fedosov