指标: 沙夫 (Schaff) 趋势周期 - Jurik Volty 自适应 RSX
当改变时间框架或设置时，指标有时会变得很奇怪。
yunnon:
当改变时间框架或设置时，指标有时会变得很奇怪。
当改变时间框架或设置时，指标有时会变得很奇怪。
这是因为在某些市场条件下，volty 自适应会产生非常短的周期。
为了避免这种情况，请将第 80 行改为：......：
val[i] = iRsi(iEma(price,FastEma,i,rates_total,0)-iEma(price,SlowEma,i,rates_total,1),RsiPeriod*iVoltyCoeff(price,AdaptivePeriod,i,rates_total),i,rates_total);
当它可能产生类似这样的情况时：
改为（一种可能的解决方案） ：
val[i] = iRsi(iEma(price,FastEma,i,rates_total,0)-iEma(price,SlowEma,i,rates_total,1),MathMax(RsiPeriod*iVoltyCoeff(price,AdaptivePeriod,i,rates_total),MathMax(RsiPeriod/4.0,1)),i,rates_total);
当默认参数相同时，它将产生类似这样的结果：
PS: 我不会改变原始指标。原因之一是：在我看来，任何发布的代码中都应显示所使用功能的好坏。因此，您可以使用上面的 "修正"，但每个人都应该知道，有些方法并不 "完美"，像上面的 "修正 "是为了避免计算中使用的某些数学模型出现问题。
Mladen Rakic:
谢谢您的启发
这是因为在某些市场条件下，波动适应产生的周期非常短
为了防止这种变化，第 80 行从这里开始：
当它可以产生这样的结果时
改为这样（作为一种可能的解决方案） ：
在默认参数相同的情况下，它能产生这样的结果：
注：我不会改变原始指标。原因之一是：在我看来，任何发布的代码都应该显示出所使用方法的优点和缺点。因此，您可以使用上面的 "修正"，但每个人都应该知道，有些方法并不 "完美"，像上面的 "修正 "是为了避免计算中使用的某些数学模型出现问题。
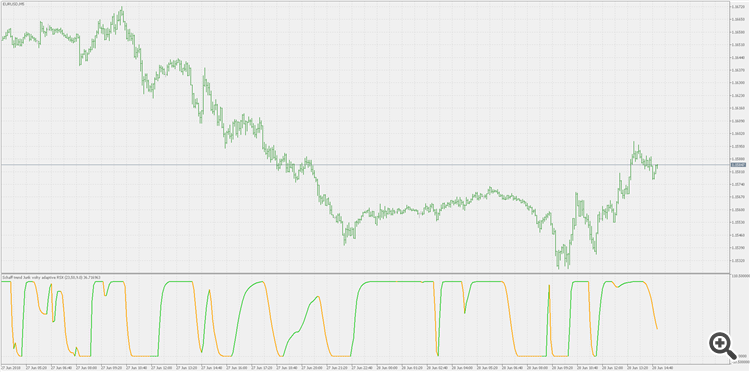
沙夫 (Schaff) 趋势周期 - Jurik Volty 自适应 RSX:
该指标是沙夫 (Schaff) 趋势周期，使用 Jurik Volty 自适应 RSX 进行计算。 默认的适应周期保持相当长，只是为了令适应的效果更加明显。
作者： Mladen Rakic