이 주제에서 나는 당신이 찾을 수 있는 확률 이론의 다양한 역설을 게시할 것을 요청합니다.
수학 퍼즐과 재미
미국의 유명한 과학 대중화자 M. Gardner의 책에는 수학의 다양한 영역에서 나온 매우 재미있는 문제와 퍼즐이 많이 포함되어 있습니다. 재료의 성공적인 선택, 완전히 특이한 프레젠테이션 형식 및 저자의 미묘한 유머는 여가 시간을 유용하게 보내고 싶어하는 수학 애호가와 같은 광범위한 독자에게 큰 즐거움을 줄 것입니다.
Alexey S. Zlygostev , E-Mail webmaster.innobi@gmail.com
mathemlib.ru
Перевод с английского Ю. А. Данилова Под редакцией Я. А. Смородинского Математические головоломки и развлечения. Пер. с англ. Ю. А. Данилова. Под ред. Я. А. Смородинского. М., "Мир", 1971, 511 с. с илл. Книга известного американского популяризатора науки М. Гарднера содержит множество весьма занимательных задач и головоломок из самых...
짝수, 홀수를 정의할 때만 "비무작위성"이 매우 두드러졌다고 생각합니다. 2보다 훨씬 큰 숫자 나누기의 나머지 부분 을 사용하는 경우 이는 감지되지 않을 것입니다.
유일한 것은 100 대신 N의 거듭제곱인 숫자(예: 64, 128, 256 ...)를 사용하는 것이 더 정확합니다.
그러나 rand()를 0에서 1 사이의 double 값으로 캐스팅하는 것도 좋은 옵션입니다. 확률 변수를 이해하는 것이 더 쉽고 가능한 한 정확하지만 조금 더 느립니다. 하지만 나노초가 될 수 있지만 나노초의 분수에 대해 이야기하고 있다고 생각합니다. int 연산이 있는 프로세서는 이중 연산( FPU / ALU 혼합) 으로 전환해야 하며 Renat는 이것이 결코 무료가 아니라고 말했습니다 .
플레이어가 추측했지만 상금을받지 못한 것을 개인적으로 본 적이 있습니까? 나는 그들의 공범자를 제외하고 아무도 승리하는 것을 본 적이 없습니다.
확률 이론에 따르면 이 3장의 카드 또는 3개의 골무는 게임의 주최측과 심지어 손재주까지 이기고 있습니다.
예, 손재주와 개연성이 없다는 이론은 없습니다. :) 모든 것이 아주 간단합니다. 나는 이것을 직접 압니다. 90년대에 이 계획에 관련된 사람이 이 계획에 대해 자세히 설명했습니다. 이제 사람들은 이에 속지 않으며 사기꾼은 주로 네트워크에서 작동합니다. 그러나 기본 원칙은 동일하게 유지됩니다. 자신의 약점을 이용해 사람을 유인해 돈을 받고, 어떤 구실을 해도 돈을 돌려받지 못한다.
당신은 당신의 내기보다 더 많이 이길 수 있습니까? 그렇지 않다면 플레이할 의미가 없습니다.
따라서 팟에서 승리할 수 있어야 합니다. 따라서 최소 내기를 하는 것으로 충분합니다. 승리가 있을 것입니다.
1회 플레이할 수 있는 조건이 있을 수 있으며 여기에서 최대 승리 확률이 있도록 내기를 결정해야 합니다.
불완전한 조건에서 모든 "pradloks"와 마찬가지로.
결정:
요금에 대한 질문도 없습니다. 내기 1. 더 이상 의미가 없습니다. 승리 확률은 내기의 크기에 의존하지 않습니다. 그래서 1, 게임을 시작합니다.
그래서 역설은 무엇입니까? 상금을 늘리려면 큰 내기를 해야 한다는 가정에서? 여기 있을 수 있습니다.
게임의 의미: 게임에 입장하기 위해서는 보증금이 필요하며 첫 번째 앞면이 나올 때까지 코인 게임이 지속됩니다(1회 게임), 첫 번째 던질 때 앞면이 나오면 1두캇 승리, 뒷면이면 1두캇, 두 번째 던질 때 머리가 빠지면 우승 금액이 두 배가 되는 식으로 머리가 나올 때까지 무한대로 계속됩니다. 1두캇을 얻을 확률은 0.5, 2-0.25, 4-0.125 등입니다. 따라서 무한대를 이길 수 있고, 뱅크의 양이 무한대이면 무한대를 플레이할 수 있습니다.
이 주제에서 나는 당신이 찾을 수 있는 확률 이론의 다양한 역설을 게시할 것을 요청합니다.
가보르 세켈리. 확률 이론과 수학 통계의 역설.
http://baguzin.ru/wp/wp-content/uploads/2016/05/Gabor-Sekey.-Paradoxes-in-probability-theory-and-mathematical-statistics.pdf
그러나 0에서 5, 또는 최대 7 또는 최대 다른 숫자가 필요한 경우? 여전히 32768.0으로 나누어야 합니다. 아니면 옵션이 있습니까?
물론 이것은 다음과 같은 질문을 던집니다.
Novaja :
이 주제에서 나는 당신이 찾을 수 있는 확률 이론의 다양한 역설을 게시할 것을 요청합니다.
수학 퍼즐과 재미
미국의 유명한 과학 대중화자 M. Gardner의 책에는 수학의 다양한 영역에서 나온 매우 재미있는 문제와 퍼즐이 많이 포함되어 있습니다. 재료의 성공적인 선택, 완전히 특이한 프레젠테이션 형식 및 저자의 미묘한 유머는 여가 시간을 유용하게 보내고 싶어하는 수학 애호가와 같은 광범위한 독자에게 큰 즐거움을 줄 것입니다.
원천:
Gardner M. '수학 퍼즐 및 엔터테인먼트' \\Danilov Yu.A.의 영어 번역, Smorodinsky Ya.A.의 편집 - 모스크바: 미르, 1971 - p.511
물론 이것은 다음과 같은 질문을 던집니다.
나눗셈의 나머지를 사용하지 않고.
나눗셈의 나머지를 사용하지 않고.
짝수, 홀수를 정의할 때만 "비무작위성"이 매우 두드러졌다고 생각합니다.
2보다 훨씬 큰 숫자 나누기의 나머지 부분 을 사용하는 경우 이는 감지되지 않을 것입니다.
유일한 것은 100 대신 N의 거듭제곱인 숫자(예: 64, 128, 256 ...)를 사용하는 것이 더 정확합니다.
그러나 rand()를 0에서 1 사이의 double 값으로 캐스팅하는 것도 좋은 옵션입니다. 확률 변수를 이해하는 것이 더 쉽고 가능한 한 정확하지만 조금 더 느립니다. 하지만 나노초가 될 수 있지만 나노초의 분수에 대해 이야기하고 있다고 생각합니다. int 연산이 있는 프로세서는 이중 연산( FPU / ALU 혼합) 으로 전환해야 하며 Renat는 이것이 결코 무료가 아니라고 말했습니다 .
이 주제에서 나는 당신이 찾을 수 있는 확률 이론의 다양한 역설을 게시할 것을 요청합니다.
https://oschool.ru/files/studys/55df78bc740d76b70e8b4287/1443032585656.pdf
플레이어가 추측했지만 상금을받지 못한 것을 개인적으로 본 적이 있습니까? 나는 그들의 공범자를 제외하고 아무도 승리하는 것을 본 적이 없습니다.
확률 이론에 따르면 이 3장의 카드 또는 3개의 골무는 게임의 주최측과 심지어 손재주까지 이기고 있습니다.
예, 손재주와 개연성이 없다는 이론은 없습니다. :) 모든 것이 아주 간단합니다. 나는 이것을 직접 압니다. 90년대에 이 계획에 관련된 사람이 이 계획에 대해 자세히 설명했습니다. 이제 사람들은 이에 속지 않으며 사기꾼은 주로 네트워크에서 작동합니다. 그러나 기본 원칙은 동일하게 유지됩니다. 자신의 약점을 이용해 사람을 유인해 돈을 받고, 어떤 구실을 해도 돈을 돌려받지 못한다.
게임의 조건은 평소와 같이 완전히 설명되어 있지 않습니다.
당신은 당신의 내기보다 더 많이 이길 수 있습니까? 그렇지 않다면 플레이할 의미가 없습니다.
따라서 팟에서 승리할 수 있어야 합니다. 따라서 최소 내기를 하는 것으로 충분합니다. 승리가 있을 것입니다.
1회 플레이할 수 있는 조건이 있을 수 있으며 여기에서 최대 승리 확률이 있도록 내기를 결정해야 합니다.
불완전한 조건에서 모든 "pradloks"와 마찬가지로.
결정:
요금에 대한 질문도 없습니다. 내기 1. 더 이상 의미가 없습니다. 승리 확률은 내기의 크기에 의존하지 않습니다. 그래서 1, 게임을 시작합니다.
그래서 역설은 무엇입니까? 상금을 늘리려면 큰 내기를 해야 한다는 가정에서? 여기 있을 수 있습니다.
게임의 의미: 게임에 입장하기 위해서는 보증금이 필요하며 첫 번째 앞면이 나올 때까지 코인 게임이 지속됩니다(1회 게임), 첫 번째 던질 때 앞면이 나오면 1두캇 승리, 뒷면이면 1두캇, 두 번째 던질 때 머리가 빠지면 우승 금액이 두 배가 되는 식으로 머리가 나올 때까지 무한대로 계속됩니다. 1두캇을 얻을 확률은 0.5, 2-0.25, 4-0.125 등입니다. 따라서 무한대를 이길 수 있고, 뱅크의 양이 무한대이면 무한대를 플레이할 수 있습니다.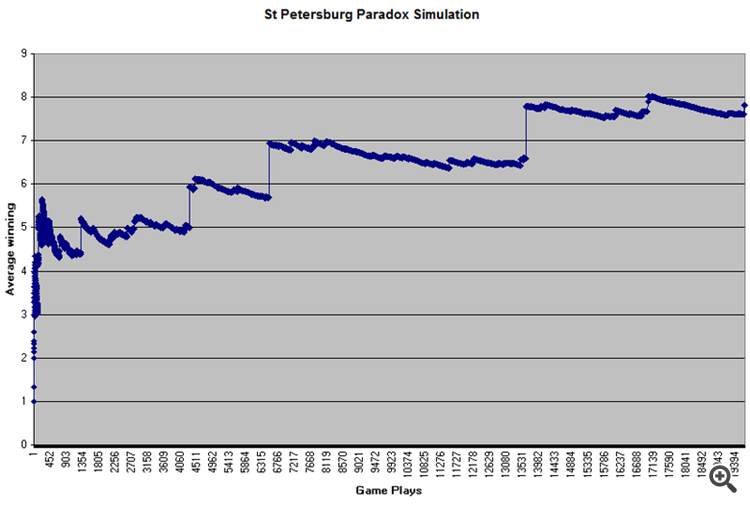
비선형 함수입니다.
y=2^x.
X가 무한대인 경우 비선형 함수에서 Y는 어디에서 경향이 있습니까? 맞습니다, 무한대로.
따라서 게임 수 = 무한대인 경우 평균 보수 = 무한대입니다.
그의 손실은 선형 함수(항상 각각 25루블)이고 그의 이득은 비선형 함수가 되도록 작업이 설정됩니다.
두 개의 함수를 플로팅해야 합니다. 먼저 첫 번째 그래프 가 두 번째 그래프보다 높으면 위치가 바뀝니다.
그것은 모두 게임 수에 달려 있습니다.
맞아요.
그러나 0에서 5, 또는 최대 7 또는 최대 다른 숫자가 필요한 경우? 여전히 32768.0으로 나누어야 합니다. 아니면 옵션이 있습니까?
1. RNG의 품질이 만족스럽지 않은 경우(예: 낮은 비트), 예를 들어 AES를 추가로 통과해야 합니다.
2. 나눗셈의 나머지를 취할 수 있지만, 2의 거듭제곱으로 나눈 경우에만 가능합니다. 그렇지 않으면 RNG의 품질이 아무리 높아도 출력이 균일 분포와 같지 않습니다.
3. 이중으로 나누면 비교가 매우 나빠질 수 있습니다. :-) 대부분의 경우 크기는 작지만 왜곡됩니다.
0과 6 사이의 난수를 얻으려면(7 중 하나):
- 제한=RAND_MAX 고려 - (RAND_MAX%7) ; 0..RAND_MAX 범위에서 7의 최대 배수
- r<limit가 될 때까지 RNG로 전환합니다. 즉, "난수"가 제한보다 크면 아무 것도 할 수 없습니다.
- 결과 = r % 7 또는 (맛과 색에 따라 다름) r * 7 / 한계
이와 같은 :-) 잘못될 수 있습니다. + -1,