그것은 실제로 매트릭스와 같습니다. 모두가 보이지만 보지는 않습니다. 모든 아파트와 트렌드에는 시작이 있고 끝이 있습니다. 당신은 동지 매트릭스에 있습니다. 버튼조차도 : Mobius가 명령 한 것처럼 빨간색과 파란색) 추가 토론을 위해 Zeon으로 돌아갈 것을 제안합니다))
나는 증가분의 분포와 시세를 읽는 간격에 따라 통계적 모멘트가 어떻게 변하는지 살펴보고 시장 가격에는 자기 유사성 속성이 없다는 것을 이해합니다. 이 속성은 브라운 운동과 같이 안정적이고 무한히 나눌 수 있는(예: 정규) 증분 분포가 있는 프로세스에만 고유합니다. 이것은 시장에서 볼 수 없습니다.
분명히 Mandelbrot와 그의 공범자들은 물리학을 더듬지 않고(더 나쁘게는 뒤지지만 조심스럽게 숨겼습니다) 고의적으로 고통받는 사람들을 오도하여 진드기 데이터와 작은 기간에 대한 스캘핑으로 신속하게 전환하고 예금을 고갈시키고 바닥을 채우지 못했습니다. 주머니.
The code in this iPython notebook used to be in R. I am very grateful to Yves Hilpisch and Michael Schwed for translating my R-code to Python. For slideshow functionality I use RISE by Damián Avila. $$ \newcommand{\beas}{\begin{eqnarray*}} \newcommand{\eeas}{\end{eqnarray*}} \newcommand{\bea}{\begin{eqnarray}} \newcommand{\eea}{\end{eqnarray}}...
나는 증가분의 분포와 시세를 읽는 간격에 따라 통계적 모멘트가 어떻게 변하는지 살펴보고 시장 가격에는 자기 유사성 속성이 없다는 것을 이해합니다. 이 속성은 브라운 운동과 같이 안정적이고 무한히 나눌 수 있는(예: 정규) 증분 분포가 있는 프로세스에만 고유합니다. 이것은 시장에서 볼 수 없습니다.
분명히 Mandelbrot와 그의 공범자들은 물리학을 더듬지 않고(심지어 더 나쁘게는 뒤지지만 조심스럽게 숨겼습니다) 고의적으로 고통받는 사람들을 오도하여 진드기 데이터와 짧은 기간에 대한 스캘핑으로 빠르게 전환하고 예금을 고갈시키고 바닥을 채우지 못했습니다. 주머니.
여전히 그가 차트를 작성하는 데 사용하는 역사 섹션을 추측하기 위해 몇 개월 동안의 추세 섹션이 있고 플랫이 있습니다.
M1에서 M5로 "점프"하는 원리가 명확하지 않은 것처럼 여기에서는 불변성 또는 최소한 정당화가 필요하므로 국가 통계 기관에 가야합니다. 거기에 그러한 재능이 있으면 그는 가격이 없을 것입니다. 그들은 또한 성공적으로 분기, 그 다음 달, 계절을 합산합니다 = 출력에서 필요한 통계 데이터
나는 60번째 순서의 Erlang 스트림에서 작업을 시작했습니다(틱 따옴표 읽기, 평균적으로 분당 1회).
EURJPY 쌍과 같은 증분에 대한 다음 히스토그램이 있습니다.
통계:
이것은 실질적으로 라플라스 분포입니다.
증분의 합(~price)과 증분 모듈(~dispersion)은 그러한 CV의 충분히 큰 표본 크기(M1의 경우 하루 또는 M5의 경우 일주일)로 정규 분포를 따릅니다.
따라서 작업은 순수한 라플라스 분포에 도달하는 것입니다. 그러면 실제로 평균으로 돌아가는 Ornstein-Uhlenbeck 과정의 직접적인 유사체를 갖게 됩니다.
일반적으로 첨도가 감소하고 꼬리가 선택되는 것이 분명합니다. ---> Laplace에서 우리는 normal로, normal에서 uniform 으로 전달합니다. 맨 처음에는 어떻습니까? 라플라스 아님? 뭐라고요? 결국 한쪽을 취하면 지수로 쉽게 설명이 됩니다. 분 EURUSD 창 월입니다.
Kolmogorov는 모니터를 응시하는 대부분의 사람들보다 똑똑한 삼촌입니다. 그리고 VR을 예측하기 위한 그의 요구 사항은 간단합니다. 예상 = const 및 주기적 ACF입니다.
이제 할 말이 있습니다.
나는 증가분의 분포와 시세를 읽는 간격에 따라 통계적 모멘트가 어떻게 변하는지 살펴보고 시장 가격에는 자기 유사성 속성이 없다는 것을 이해합니다. 이 속성은 브라운 운동과 같이 안정적이고 무한히 나눌 수 있는(예: 정규) 증분 분포가 있는 프로세스에만 고유합니다. 이것은 시장에서 볼 수 없습니다.
분명히 Mandelbrot와 그의 공범자들은 물리학을 더듬지 않고(더 나쁘게는 뒤지지만 조심스럽게 숨겼습니다) 고의적으로 고통받는 사람들을 오도하여 진드기 데이터와 작은 기간에 대한 스캘핑으로 신속하게 전환하고 예금을 고갈시키고 바닥을 채우지 못했습니다. 주머니.
그게 다야!
주제에 대한 연구
http://tpq.io/p/rough_volatility_with_python.html
동일 https://hal.inria.fr/hal-01350915/document이제 할 말이 있습니다.
나는 증가분의 분포와 시세를 읽는 간격에 따라 통계적 모멘트가 어떻게 변하는지 살펴보고 시장 가격에는 자기 유사성 속성이 없다는 것을 이해합니다. 이 속성은 브라운 운동과 같이 안정적이고 무한히 나눌 수 있는(예: 정규) 증분 분포가 있는 프로세스에만 고유합니다. 이것은 시장에서 볼 수 없습니다.
분명히 Mandelbrot와 그의 공범자들은 물리학을 더듬지 않고(심지어 더 나쁘게는 뒤지지만 조심스럽게 숨겼습니다) 고의적으로 고통받는 사람들을 오도하여 진드기 데이터와 짧은 기간에 대한 스캘핑으로 빠르게 전환하고 예금을 고갈시키고 바닥을 채우지 못했습니다. 주머니.
그게 다야!
당신은 이미 음모론을 여기로 끌어들였습니다... 또 다른 말도 안되는 소리입니다.
주제에 익숙해지기:
http://inis.jinr.ru/sl/vol2/Physics/Dynamical%20systems%20i%20Chaos/Feder%20E.,%20Fractals,%201991.pdf
내가 찾고 있는 것을 명확히 하기 위해.
나는 60번째 순서의 Erlang 스트림에서 작업을 시작했습니다(틱 따옴표 읽기, 평균적으로 분당 1회).
EURJPY 쌍과 같은 증분에 대한 다음 히스토그램이 있습니다.
통계:
이것은 실질적으로 라플라스 분포입니다.
증분의 합(~price)과 증분 모듈(~dispersion)은 그러한 CV의 충분히 큰 표본 크기(M1의 경우 하루 또는 M5의 경우 일주일)로 정규 분포를 따릅니다.
따라서 작업은 순수한 라플라스 분포에 도달하는 것입니다. 그러면 실제로 평균으로 돌아가는 Ornstein-Uhlenbeck 과정의 직접적인 유사체를 갖게 됩니다.
여전히 그가 차트를 작성하는 데 사용하는 역사 섹션을 추측하기 위해 몇 개월 동안의 추세 섹션이 있고 플랫이 있습니다.
M1에서 M5로 "점프"하는 원리가 명확하지 않은 것처럼 여기에서는 불변성 또는 최소한 정당화가 필요하므로 국가 통계 기관에 가야합니다. 거기에 그러한 재능이 있으면 그는 가격이 없을 것입니다. 그들은 또한 성공적으로 분기, 그 다음 달, 계절을 합산합니다 = 출력에서 필요한 통계 데이터
)))
내가 찾고 있는 것을 명확히 하기 위해.
나는 60번째 순서의 Erlang 스트림에서 작업을 시작했습니다(틱 따옴표 읽기, 평균적으로 분당 1회).
EURJPY 쌍과 같은 증분에 대한 다음 히스토그램이 있습니다.
통계:
이것은 실질적으로 라플라스 분포입니다.
증분의 합(~price)과 증분 모듈(~dispersion)은 그러한 CV의 충분히 큰 표본 크기(M1의 경우 하루 또는 M5의 경우 일주일)로 정규 분포를 따릅니다.
따라서 작업은 순수한 라플라스 분포에 도달하는 것입니다. 그러면 실제로 평균으로 돌아가는 Ornstein-Uhlenbeck 과정의 직접적인 유사체를 갖게 됩니다.
일반적으로 첨도가 감소하고 꼬리가 선택되는 것이 분명합니다. ---> Laplace에서 우리는 normal로, normal에서 uniform 으로 전달합니다. 맨 처음에는 어떻습니까? 라플라스 아님? 뭐라고요? 결국 한쪽을 취하면 지수로 쉽게 설명이 됩니다.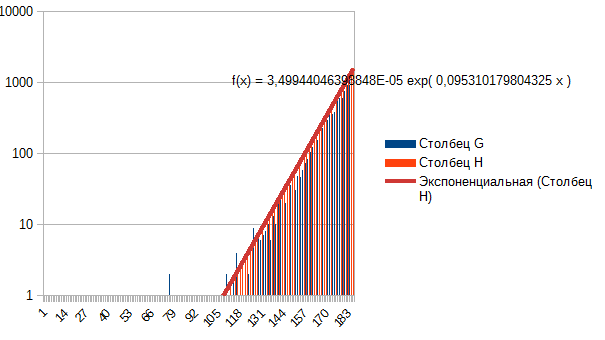
분 EURUSD 창 월입니다.