この表を見てください:
これを繰り返すと、違う結果になります:
| 0行目 | 0 | 0 | 0 | 0 |
| 1行目 | 1 | 1 | 1 | 1 |
| 2列目 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| 計算1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| 計算2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| 計算3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| 3行目 | 1 - 2x + x^2 | -1 +5x + x^2 |
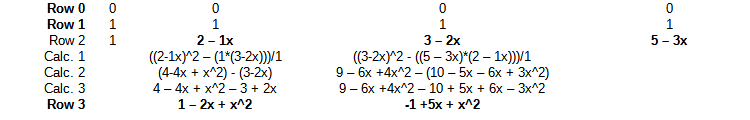
Carl Schreiber #:
この表を見てください:
これを繰り返すと、違う結果になります:
| 0行目 | 0 | 0 | 0 | 0 |
| 1行目 | 1 | 1 | 1 | 1 |
| 2列目 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| 計算1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| 計算2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| 計算3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| 3行目 | 1 - 2x + x^2 | -1 +5x + x^2 |
こんにちは、
ちょうどこれを見たところです。見て、元に戻します。
申し訳ない。
あなたの例しかないようです(本当にこの例が必要なのでしょうか)。
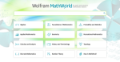
| 0行目 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1行目 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2列目 | 1 | 2 - 1x | 3 - 2x | 5 - 3x | 8 - 5x | 13 - 8x | 31 - 13x |
| 計算1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | (5 - 3x)^2 - ( (3 - 2x)(8 - 5x)) | (8 - 5x)^2 - (5 - 3x)(13 - 8x) | (13 - 8x)^2 - ( (8 - 5x)(31 - 13x) ) | ||
| 計算2 | (4 - 4x + x^2) - (3 - 2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | 25 - 30x + 9x^2 - (24 - 15x + 16x + 10x^2) | 64 - 80x +25x^2 - (65 - 39x - 40x + 24x) | 169 - 208x + 64x^2 - (248 - 104x - 155x + 65x^2) | ||
| 計算3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | 25 - 30x + 9x^2 - 24 + 15x - 16x - 10x^2) | 64 - 80x +25x^2 - 65 + 39x + 40x - 24x) | 169 - 208x + 64x^2 - 248 + 104x + 155x - 65x^2) | ||
| 3行目 | 1 - 2x + x^2 | -1 +5x + x^2 | 1 - 31x - x^2 | -1 - 1x + x^2 | -79 - 51x - 1x^2 |
Quotient-Difference Table -- from Wolfram MathWorld
- mathworld.wolfram.com
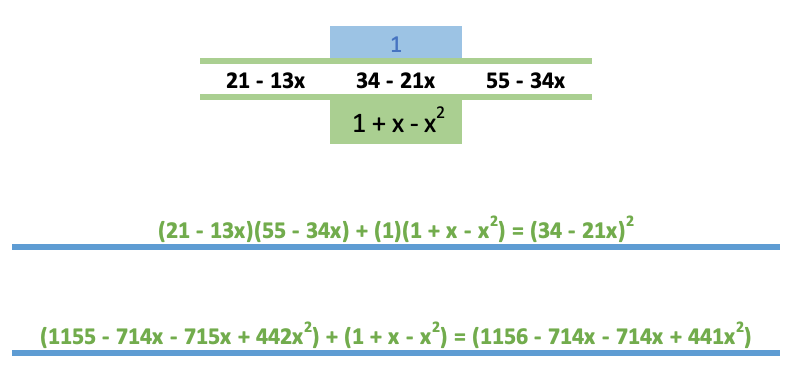
A quotient-difference table is a triangular array of numbers constructed by drawing a sequence of n numbers in a horizontal row and placing a 1 above each. An additional "1" is then placed at the beginning and end of the row of 1s, and the value of rows underneath the original row is then determined by looking at groups of adjacent numbers N ; W X E; S (1) and computing S=(X^2-EW)/N (2) for the elements falling within a triangle formed by the diagonals extended from the...
ファイル:
https:// www.mql5.com/en/forum/461644#comment_53343777

Discussing the article: "MQL5 Wizard Techniques you should know (Part 11): Number Walls"
- 2024.01.31
- MetaQuotes
- www.mql5.com
Check out the new article: MQL5 Wizard Techniques you should know (Part 11): Number Walls . Author: Stephen Njuki...
取引の機会を逃しています。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索

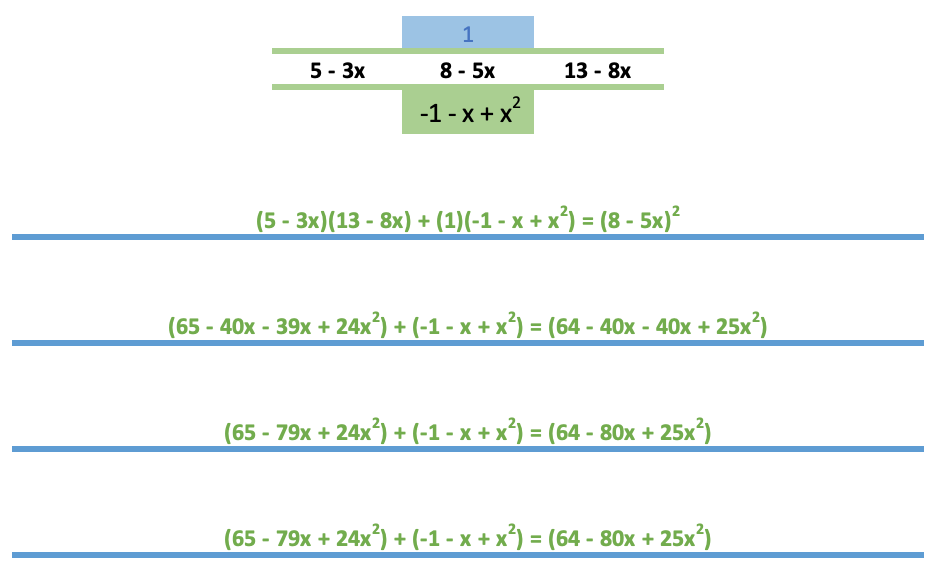
新しい記事「知っておくべきMQL5ウィザードのテクニック(第11回):ナンバーウォール」はパブリッシュされました:
ナンバーウォールは、リニアシフトバックレジスタの一種で、収束を確認することにより、予測可能な数列を事前にスクリーニングします。これらのアイデアがMQL5でどのように役立つかを見ていきます。
2、3の時系列については、その中に現れた過去の値に基づいて、数列の次の値の計算式を考案することが可能です。ナンバーウォールは、「クロスルール」と呼ばれるものを介して行列の形で「数値の壁」を事前に生成することによって、これを達成することができます。この行列を生成する際の第一の目的は、問題の数列が収束しているかどうかを確認することです。数列を適用した後、行列の後続の行が0だけであれば、数列のナンバーウォールのクロスルールアルゴリズムはこの問いに喜んで答えます。
この論文では、これらの概念を示すために、ローラン冪級数(別名フォーマルローラン級数、FLS)を、コーシー積を用いながら、多項式形式で演算してこれらの数列を表現する枠組みとして用いています。
ウィザードで組み立てたEAの比較テストを以下に示します。どちらもAwesome Oscillatorシグナルを使用し、ここに示されているように、基本的には同じような入力を持っています。
両者の違いは、一方のEAがParabolic SARを使用して未決済ポジションをトレールしクローズするのに対し、もう一方はこの記事で紹介したナンバーウォールアルゴリズムを使用していることです。過去1年間のEURUSDを1時間足で検証した場合、同じシグナルにもかかわらず、両者のレポートは異なっています。まず、Parabolic SARのトレール注文のEAです。
作者: Stephen Njuki