Domanda: Come posso valutare correttamente i risultati?
L'errore di ogni modulo è dato come percentuale. Lo 0% è il risultato ideale.
| ________________ PARAMETRI ________________ | Mod 1 | Mod 2 | Mod 3 | Modo 4 | Modo 5 | (vi) Modo 6 | (vi) Modo 7 | (vi) Modo 8 | (vi) Mod 9 | (vi) Mod 10 | (vi) Mod 11 | (vi) Mod 12 | (viii) mod 13 | (vi) 14 | Modo 15 | Errore medio | Dai tentativi |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND | 4,43 | 17,09 | 15,82 | 2,53 | 0,63 | 17,72 | 28,48 | 5,70 | 13,29 | 5,70 | 8,23 | 6,33 | 0,63 | 3,16 | 6,96 | 9,11 | 158,00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1 | 5,06 | 17,72 | 12,66 | 3,80 | 0,63 | 19,62 | 29,11 | 4,43 | 9,49 | 5,06 | 6,33 | 6,33 | 1,90 | 1,90 | 6,33 | 8,69 | 158,00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2 | 4,43 | 20,25 | 16,46 | 4,43 | 0,63 | 17,72 | 29,75 | 6,33 | 5,06 | 8,23 | 10,13 | 5,06 | 0,63 | 1,27 | 4,43 | 8,99 | 158,00 |
Voglio che l'errore di ogni modulo sia minimo, ma voglio anche che la diffusione sia minima.
prodotto di logaritmi
ZS: non so bene cosa sia richiesto, ma il logaritmo permetterà di trattare gli errori in modo progressivo, darà risultati migliori nei casi singoli (moduli individuali). E la moltiplicazione è un tentativo di ridurre la dispersioneprodotto di logaritmi
ZS: Non capisco bene cosa sia richiesto esattamente, ma il logaritmo permetterà di trattare gli errori progressivamente, darà risultati migliori nei casi singoli (moduli individuali). E la moltiplicazione è un tentativo di ridurre la diffusioneGrazie. Epraticamente com'è?
Grazie. Epraticamente com'è?
Probabilmente solo il prodotto di
Opzione1 ) Traduci ogni modulo nello stile (1-x%) e moltiplicalo..... il risultato è anche sottratto dall'unità.
x% è il valore della cella
Opzione2
Con i logaritmi prendiamo semplicemente il valore di una cella e contiamo il logaritmo da esso)))) il più vicino al valore zero è alla valutazione progressiva cioè con qualche impostazione di base 0,1 è meglio di 0,01 e anche 0,1 è meglio di 1. Ci sarà solo un parametro di base per il logaritmo con cui vale la pena giocare.
Forse un semplice prodotto andrebbe bene.
Opzione1 ) Traduci ogni modulo nello stile (1-x%) e moltiplicali..... Il risultato è anche sottratto dall'unità.
x% è il valore della cella
Opzione2
Con i logaritmi prendiamo semplicemente il valore di una cella e contiamo il logaritmo da esso)))) il più vicino al valore zero è alla valutazione progressiva cioè con qualche impostazione di base 0,1 è meglio di 0,01 e anche 0,1 è meglio di 1. Ci sarà solo un parametro base del logaritmo con cui vale la pena giocare.
Opzione 1
| -3,43 | -16,09 | -14,82 | -1,53 | 0,37 | -16,72 | -27,48 | -4,70 | -12,29 | -4,70 | -7,23 | -5,33 | 0,37 | -2,16 | -5,96 | 10601305851,38 |
| -4,06 | -16,72 | -11,66 | -2,80 | 0,37 | -18,62 | -28,11 | -3,43 | -8,49 | -4,06 | -5,33 | -5,33 | -0,90 | -0,90 | -5,33 | -6223799946,09 |
| -3,43 | -19,25 | -15,46 | -3,43 | 0,37 | -16,72 | -28,75 | -5,33 | -4,06 | -7,23 | -9,13 | -4,06 | 0,37 | -0,27 | -3,43 | 1237520122,21 |
Cosa mi dice questo?
Opzione 2
| -0,64640373 | -1,23274206 | -1,19920648 | -0,40312052 | 0,200659451 | -1,24846372 | -1,45453998 | -0,75587486 | -1,12352498 | -0,75587486 | -0,91539984 | -0,80140371 | 0,200659451 | -0,49968708 | -0,84260924 |
| -0,70415052 | -1,24846372 | -1,10243371 | -0,5797836 | 0,200659451 | -1,292699 | -1,46404221 | -0,64640373 | -0,97726621 | -0,70415052 | -0,80140371 | -0,80140371 | -0,2787536 | -0,2787536 | -0,80140371 |
| -0,64640373 | -1,30642503 | -1,21642983 | -0,64640373 | 0,200659451 | -1,24846372 | -1,47348697 | -0,80140371 | -0,70415052 | -0,91539984 | -1,00560945 | -0,70415052 | 0,200659451 | -0,10380372 | -0,64640373 |
Questo è il logaritmo con base 0,1
Cosa dovrei farci?
Ho provato altre funzioni. Solo che come faccio a capirli anche io? ....
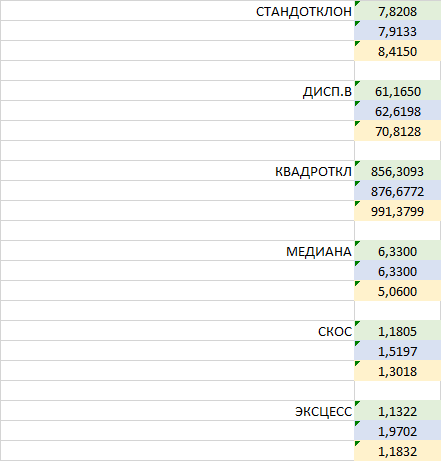
| STANDOTCLONE | 7,8208 |
| 7,9133 | |
| 8,4150 | |
| DISP.B | 61,1650 |
| 62,6198 | |
| 70,8128 | |
| QUADROTKL | 856,3093 |
| 876,6772 | |
| 991,3799 | |
| MEDIANA | 6,3300 |
| 6,3300 | |
| 5,0600 | |
| SCOS | 1,1805 |
| 1,5197 | |
| 1,3018 | |
| ECCESSO | 1,1322 |
| 1,9702 | |
| 1,1832 |
Trova il massimo in ogni riga, poi scegli la riga con il massimo minimo. Perdona il gioco di parole))
Massimo massimo nella linea 3, minimo massimo nella linea 1. И? )))
Massimo massimo nella linea 3, minimo massimo nella linea 1. И? )))
Scegliete la prima linea.
Opzione 1
| -3,43 | -16,09 | -14,82 | -1,53 | 0,37 | -16,72 | -27,48 | -4,70 | -12,29 | -4,70 | -7,23 | -5,33 | 0,37 | -2,16 | -5,96 | 10601305851,38 |
| -4,06 | -16,72 | -11,66 | -2,80 | 0,37 | -18,62 | -28,11 | -3,43 | -8,49 | -4,06 | -5,33 | -5,33 | -0,90 | -0,90 | -5,33 | -6223799946,09 |
| -3,43 | -19,25 | -15,46 | -3,43 | 0,37 | -16,72 | -28,75 | -5,33 | -4,06 | -7,23 | -9,13 | -4,06 | 0,37 | -0,27 | -3,43 | 1237520122,21 |
Cosa mi dice questo?
Opzione 2
| -0,64640373 | -1,23274206 | -1,19920648 | -0,40312052 | 0,200659451 | -1,24846372 | -1,45453998 | -0,75587486 | -1,12352498 | -0,75587486 | -0,91539984 | -0,80140371 | 0,200659451 | -0,49968708 | -0,84260924 |
| -0,70415052 | -1,24846372 | -1,10243371 | -0,5797836 | 0,200659451 | -1,292699 | -1,46404221 | -0,64640373 | -0,97726621 | -0,70415052 | -0,80140371 | -0,80140371 | -0,2787536 | -0,2787536 | -0,80140371 |
| -0,64640373 | -1,30642503 | -1,21642983 | -0,64640373 | 0,200659451 | -1,24846372 | -1,47348697 | -0,80140371 | -0,70415052 | -0,91539984 | -1,00560945 | -0,70415052 | 0,200659451 | -0,10380372 | -0,64640373 |
Questo è il logaritmo con base 0,1
Cosa dovrei farci?
Ho provato altre funzioni. Ma come faccio a capire anche loro?
L'errore di ogni modulo è dato in percentuale. 0% è il risultato ideale". Il numero 1 significa 100% - x% o 1-X*0.01

| TOTALE | ||||||||||||||||
| 0,9557 | 0,8291 | 0,8418 | 0,9747 | 0,9937 | 0,8228 | 0,7152 | 0,943 | 0,8671 | 0,943 | 0,9177 | 0,9367 | 0,9937 | 0,9684 | 0,9304 | 0,77439 | |
| 0,9494 | 0,8228 | 0,8734 | 0,962 | 0,9937 | 0,8038 | 0,7089 | 0,9557 | 0,9051 | 0,9494 | 0,9367 | 0,9367 | 0,981 | 0,981 | 0,9367 | 0,758606 | |
| 0,9557 | 0,7975 | 0,8354 | 0,9557 | 0,9937 | 0,8228 | 0,7025 | 0,9367 | 0,9494 | 0,9177 | 0,8987 | 0,9494 | 0,9937 | 0,9873 | 0,9557 | 0,771806 |
la seconda linea è la migliore, e la prima e la terza sono molto simili
il totale sottratto dall'unità, cioè più è vicino a 0 il totale, migliori sono i risultati..... in altre parole, i risultati finora non sono molto buoni perché 0,75 è il tuo 75, anche se dipende da con cosa confrontarlo..... il peggior punteggio sarebbe 1 (100%) il miglior punteggio 0
Dovete capire che un punteggio di 90 è dieci volte meglio di un punteggio di 99.... un punteggio di 99 è dieci volte meglio di un punteggio di 99,9... 100 è infatti possibile solo quando tutti i moduli hanno un punteggio di errore di 100... cioè un punteggio di 0,1 è dieci volte peggiore di un punteggio di 0,01. Allo stesso tempo, un punteggio di 10 è dieci volte peggiore di un punteggio di 1.
con il logaritmo su think..... la risposta dovrebbe essere esclusivamente valori positivi... di solito un logaritmo di 1,1... nell'intervallo da 1 a 2, non da 0 a 1.... se vogliono aumentare il numero e da 2 se vogliono diminuirlo progressivamente
Il metodo della deviazione quadratica è decisamente fuori questione. Così come tutti gli altri che contano le deviazioni. Perché idealmente la deviazione quadratica da una regressione lineare sarebbe usata per capire la varianza. Ma poi otteniamo una stima di queste deviazioni senza alcuna media dei numeri stessi.....
Domanda: Come posso valutare correttamente i risultati?
L'errore di ogni modulo è dato come percentuale. Lo 0% è il risultato ideale.
| ________________ PARAMETRI ________________ | Mod 1 | Mod 2 | Mod 3 | Modo 4 | Modo 5 | (vi) mod 6 | (vi) Modo 7 | (vi) Modo 8 | (vi) Mod 9 | (vi) Mod 10 | (vi) Mod 11 | (vi) Mod 12 | (viii) mod 13 | (vi) 14 | Modo 15 | Errore medio | Dai tentativi |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND | 4,43 | 17,09 | 15,82 | 2,53 | 0,63 | 17,72 | 28,48 | 5,70 | 13,29 | 5,70 | 8,23 | 6,33 | 0,63 | 3,16 | 6,96 | 9,11 | 158,00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1 | 5,06 | 17,72 | 12,66 | 3,80 | 0,63 | 19,62 | 29,11 | 4,43 | 9,49 | 5,06 | 6,33 | 6,33 | 1,90 | 1,90 | 6,33 | 8,69 | 158,00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2 | 4,43 | 20,25 | 16,46 | 4,43 | 0,63 | 17,72 | 29,75 | 6,33 | 5,06 | 8,23 | 10,13 | 5,06 | 0,63 | 1,27 | 4,43 | 8,99 | 158,00 |
Voglio che l'errore di ogni modulo sia minimo, ma voglio anche che la dispersione sia minima.
Probabilmente è meglio ottenere la somma dei quadrati per gli errori del modulo, ed estrarre la radice.
Così, otterremo la stima dell'errore totale del modulo.
Più questo valore è vicino allo zero, meglio è.
Quindi va così.
//+------------------------------------------------------------------+ //| EstimateError.mq5 | //| Copyright 2020, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2020, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" double ModN[15][3] = {{4.43, 5.06, 4.43}, {17.09, 17.72, 20.25}, {15.82, 12.66, 16.46}, {2.53, 3.80, 4.43}, {0.63, 0.63, 0.63}, {17.72, 19.62, 17.72}, {28.48, 29.11, 29.75}, {5.70, 4.43, 6.33}, {13.29, 9.49, 5.06}, {5.70, 5.06, 8.23}, {8.23, 6.33, 10.13}, {6.33, 6.33, 5.06}, {0.63, 6.33, 0.63}, {3.16, 1.90, 1.27}, {6.96, 6.33, 4.43}}; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { double ModX[]; ArrayResize(ModX, 3); ZeroMemory(ModX); int num = 1; double est = 0.0; for(int i=0; i<15; i++) { for(int j=0; j<3; j++) { ModX[j] = ModN[i][j]; } est = EstimateError(ModX); PrintFormat("Mod"+(string)num+" EstimateError: %.3f", est); num++; } }// End OnStart //+------------------------------------------------------------------+ double EstimateError(double & arr[]) { int size = ArraySize(arr); if(size == 0 || size < 3) return(0.0); //double avg = ArrayMean(arr); double max = ArrayMax(arr); double min = ArrayMin(arr); double sum_sqr_e = 0.0; double est_e = 0.0; for(int i=0; i<size; i++) sum_sqr_e += MathPow(arr[i] - (max-min)/* или avg*/, 2.0) / (size - 2.0); est_e = MathSqrt(sum_sqr_e); return(est_e); } //+------------------------------------------------------------------- //Возвращает максимальное значение элементов массива double ArrayMax(double & arrIn[]) { uint size = ArraySize(arrIn); if(size == 0) return(0.0); double max = arrIn[0]; for(uint i=1; i<size; i++) if(arrIn[i] > max) max = arrIn[i]; return(max); } //-------------------------------------------------------------------- //Возвращает минимальное значение элементов массива double ArrayMin(double & arrIn[]) { uint size = ArraySize(arrIn); if(size == 0) return(0.0); double min = arrIn[0]; for(uint i=1; i<size; i++) if(arrIn[i] < min) min = arrIn[i]; return(min); } //-------------------------------------------------------------------- //Возвращает средне арефметическое значение элементов массива double ArrayMean(double & arrIn[]) { uint size = ArraySize(arrIn); if(size == 0) return(0.0); double sum = 0.0; for(uint i=0; i<size; i++) sum += arrIn[i]; return(sum/size); } //--------------------------------------------------------------------
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod1 EstimateError: 6.965 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod2 EstimateError: 26.422 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod3 EstimateError: 19.577 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod4 EstimateError: 3.226 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod5 EstimateError: 1.091 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod6 EstimateError: 28.540 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod7 EstimateError: 48.234 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod8 EstimateError: 6.361 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod9 EstimateError: 6.102 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod10 EstimateError: 5.965 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod11 EstimateError: 8.130 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod12 EstimateError: 8.098 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod13 EstimateError: 7.198 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod14 EstimateError: 1.413 2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5) Mod15 EstimateError: 6.138
La stima mostra che Mod5 ha l'errore più piccolo.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Domanda: Come posso valutare correttamente i risultati?
L'errore di ogni modulo è dato come percentuale. Lo 0% è il risultato ideale.
Vorrei che l'errore di ogni modulo fosse minimo, ma vorrei anche che la diffusione fosse minima.