...
C'è una montagna di paradossi nelle terzine e matstate non amate qui :-)
Perché la teoria della probabilità e la statistica sono improvvisamente diventate poco amate qui? Sembra che qui stiano bene. Ma con sciocchezze basate sulla teoria della probabilità e problemi di statistica.
Quali sono i paradossi?
Einstein e il GTR/STO, in generale è forte.
"c'è un enorme rospo che vola verso di te a 0,97C; riesci a capire che è un rospo?".
Perché la teoria della probabilità e la statistica sono improvvisamente poco amate qui? Sembra che stiano bene qui. Ma ci sono problemi con le sciocchezze basate sulla teoria della probabilità e la statistica.
Quali sono i paradossi?
È possibile in MT4 testare automaticamente un EA in ordine decrescente di tempo da testare? Per esempio dal 2015.01.01 al 2015.12.31, passo successivo dal 2015.01.02 al 2015.12.31 e così via.
Risolvo questo problema usando l'ottimizzatore:
//+------------------------------------------------------------------+ // Внешние переменные input bool CheckEvery_Day=false; input bool TestEachYearSeparately=false; input int DayOfYear_=1; input int Year_=2009; // Эксперт функция тик void OnTick(void) { if(CheckEvery_Day) { if(TestEachYearSeparately) if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_) || Year()>Year_) return; //тестировать каждый год отдельно else if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_)) return; //тестировать весь период } // Ваш код } //+------------------------------------------------------------------+
Scegli un periodo di tempo:
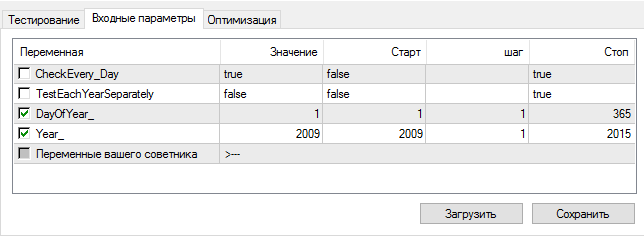
Attivare Optimizer:
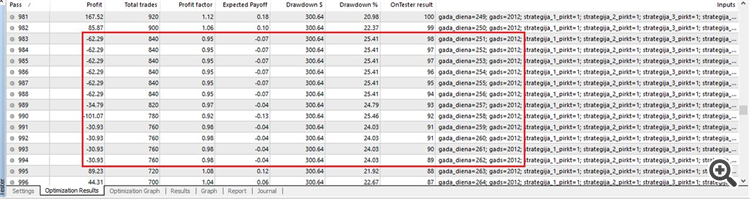
Otteniamo il risultato, dove si può vedere come l'Expert Advisor supera il test ogni volta a partire da un nuovo giorno:
Perché la teoria della probabilità e la statistica sono improvvisamente poco amate qui? Sembra che stiano bene qui. Ma c'è un problema con le sciocchezze basate sulla teoria della probabilità e la statistica.
E quali paradossi?
È la prima volta che sentite parlare di paradossi TV e MC?
Ecco, date un'occhiata. Ci sono molti buoni esempi:
SEKAI G / PARADOSSI IN TEORIA DELLA PROBABILITÀ E STATISTICA MATEMATICA
Categoria:Matematica 11 marzo 2010Titolo: Paradossi nella teoria della probabilità e nella statistica matematica
Autore: Sekei G.
Abstract: Un libro di un matematico ungherese che contiene una raccolta di conclusioni e affermazioni inaspettate dalla teoria della probabilità, dalla statistica matematica e dalla teoria dei processi casuali È scritto in modo vivido e affascinante, il materiale presentato in esso può essere utilizzato per illustrare nelle lezioni universitarie sulla teoria della probabilità, e alcune sezioni possono essere utilizzate nel lavoro dei circoli scolastici di matematica
Per matematici di varie qualifiche, per tutti gli studenti di teoria della probabilità e statistica matematica
Scarica in pdf (11,4 MB ):Sekey G. / Paradossi in teoria della probabilità e statistica matematica
vixri.com.
È la prima volta che sentite parlare di paradossi della TV e della SM?
Guarda qui. Ci sono molti buoni esempi:
SECEI G / PARADOSSI IN TEORIA DELLA PROBABILITÀ E STATISTICA MATEMATICA
Categoria:Matematica 11 marzo 2010Titolo: Paradossi nella teoria della probabilità e nella statistica matematica.
Autore: Sekei G.
Abstract: Il libro del matematico ungherese che contiene una raccolta di scoperte e affermazioni inaspettate dalla teoria della probabilità, dalla statistica matematica e dalla teoria dei processi casuali. È scritto in modo vivace e affascinante, e il materiale ivi presentato può essere utilizzato per l'illustrazione nelle lezioni universitarie sulla teoria della probabilità, mentre alcune sezioni possono essere utilizzate nel lavoro dei circoli matematici scolastici.
Per matematici di varie qualifiche, per tutti gli studenti di teoria della probabilità e statistica matematica
Scarica in pdf (11,4 MB ):Sekey G. / Paradossi in teoria della probabilità e statistica matematica
vixri.com.
E poi qualcosa lui stesso è in grado di scrivere con parole proprie, o solo sui link, e sugli screenshot?
Ora vado a leggere un libro. La maggior parte di questi paradossi nasce dall'ignoranza dell'autore, dall'errata formulazione del problema. Bisogna aprire gli occhi e la mente e non ci sono paradossi.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso


Il paradosso dell'onnipotenza:
Il paradosso è solitamente formulato come una domanda: "Può un dio creare una pietra che egli stesso non può sollevare?" (Penso di sì, un ciclo infinito di creazione e sollevamento)o
"Dio potrebbe creare un triangolo con angoli interni che non siano 180 gradi in totale?"(Penso di sì, geometria di Riemann).
Se a Colombo fosse stato chiesto: "È possibile andare dall'Europa all'America in 24 ore?", penso che con le possibilità dell'epoca avrebbe detto di no, ma al giorno d'oggi qualsiasi bambino dirà che è possibile. La domanda che segue è: "Questa possibilità esisteva già ai tempi di Colombo o è apparsa solo nei tempi moderni?"Teoricamente la possibilità è sempre esistita, ma in pratica è diventata disponibile solo oggi. È possibile concludere da questo che: tutto ciò che non contraddice la matematica è possibile, sia che possiamo implementarlo fisicamente o no?Le possibilità esistono sia che ne siamo consapevoli o no.