Discussione sull’articolo "Reti neurali di terza generazione: Reti profonde" - pagina 2

Nuovo commento
 
vlad1949:

Non è una domanda per me. È tutto quello che hai da dire sull'articolo?

Cosa c'è da dire sull'articolo? È una tipica riscrittura. È la stessa cosa in altre fonti, solo con parole leggermente diverse. Anche le immagini sono le stesse. Non ho visto nulla di nuovo, cioè di autoriale.

Volevo provare gli esempi, ma è un peccato. La sezione è per MQL5, ma gli esempi sono per MQL4.

 

vlad1949

Caro Vlad!

Ho guardato negli archivi, hai una documentazione R piuttosto vecchia. Sarebbe opportuno passare alle copie allegate.

File:
Doc_R.zip  2181 kb
 

vlad1949

Caro Vlad!

Perché non è riuscito a funzionare nel tester?

Ho tutto funziona senza problemi. Ma lo schema è senza indicatore: l'Expert Advisor comunica direttamente con R.

 

Jeffrey Hinton, inventore delle reti profonde: "Le reti profonde sono applicabili solo a dati in cui il rapporto segnale/rumore è elevato. Le serie finanziarie sono così rumorose che le reti profonde non sono applicabili. Ci abbiamo provato e non abbiamo avuto fortuna".

Ascoltate le sue conferenze su YouTube.

 
gpwr:

Jeffrey Hinton, inventore delle reti profonde: "Le reti profonde sono applicabili solo a dati in cui il rapporto segnale/rumore è elevato. Le serie finanziarie sono così rumorose che le reti profonde non sono applicabili. Ci abbiamo provato e non abbiamo avuto fortuna".

Ascoltate le sue lezioni su youtube.

Considerando il suo post nel thread parallelo.

Il rumore è inteso in modo diverso nei compiti di classificazione rispetto all'ingegneria radiofonica. Un predittore è considerato rumoroso se è debolmente correlato (ha un debole potere predittivo) alla variabile target. Un significato completamente diverso. Si dovrebbero cercare predittori che abbiano potere predittivo per diverse classi della variabile target.

 
Ho una concezione simile del rumore. Le serie finanziarie dipendono da un gran numero di predittori, la maggior parte dei quali è sconosciuta e introduce il "rumore" nelle serie. Utilizzando solo predittori pubblicamente disponibili, non siamo in grado di prevedere la variabile target, indipendentemente dalle reti o dai metodi utilizzati.
 
gpwr:
Ho una concezione simile del rumore. Le serie finanziarie dipendono da un gran numero di predittori, la maggior parte dei quali è sconosciuta e introduce il "rumore" nelle serie. Utilizzando solo i predittori pubblicamente disponibili, non siamo in grado di prevedere la variabile target, indipendentemente dalle reti o dai metodi utilizzati.
Si veda il mio thread.
 
faa1947:

vlad1949

Caro Vlad!

Perché non è riuscito a funzionare nel tester?

Ho tutto funziona senza problemi. Vero lo schema senza indicatore: il consulente comunica direttamente con R.

llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll

Buon pomeriggio SanSanych.

Quindi l'idea principale è quella di fare multicurrency con diversi indicatori.

Altrimenti, ovviamente, è possibile racchiudere tutto in un Expert Advisor.

Ma se la formazione, i test e l'ottimizzazione saranno effettuati al volo, senza interrompere il trading, allora la variante con un Expert Advisor sarà un po' più difficile da implementare.

Buona fortuna

PS. Qual è il risultato dei test?

 

Saluti SanSanych.

Ecco alcuni esempi di determinazione del numero ottimale di cluster che ho trovato su alcuni forum di lingua inglese. Non sono riuscito a utilizzarli tutti con i miei dati. Molto interessante il pacchetto 11 "clusterSim".

--------------------------------------------------------------------------------------

#
n = 100
g = 6 
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))), 
                y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
plot(d)
--------------------------------------
#1 
library(fpc)
pamk.best <- pamk(d)
cat("number of clusters estimated by optimum average silhouette width:", strpamk.best$nc, "\n")
plot(pam(d, pamk.best$nc))

#2 we could also do:
library(fpc)
asw <- numeric(20)
for (k in 2:20)
  asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
cat("silhouette-optimal number of clusters:", k.best, "\n")
---------------------------------------------------
#3. Calinsky criterion: Another approach to diagnosing how many clusters suit the data. In this case 
# we try 1 to 10 groups.
require(vegan)
fit <- cascadeKM(scale(d, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
# 5 clusters!
-------------------
4. Determine the optimal model and number of clusters according to the Bayesian Information 
Criterion for expectation-maximization, initialized by hierarchical clustering for parameterized 
Gaussian mixture models
library(mclust)
# Run the function to see how many clusters
# it finds to be optimal, set it to search for
# at least 1 model and up 20.
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
cat("model-based optimal number of clusters:", m.best, "\n")
# 4 clusters
plot(d_clust)
----------------------------------------------------------------
5. Affinity propagation (AP) clustering, see http://dx.doi.org/10.1126/science.1136800 
library(apcluster)
d.apclus <- apcluster(negDistMat(r=2), d)
cat("affinity propogation optimal number of clusters:", length(d.apclus@clusters), "\n")
# 4
heatmap(d.apclus)
plot(d.apclus, d)
---------------------------------------------------------------------
6. Gap Statistic for Estimating the Number of Clusters. 
See also some code for a nice graphical 
output . Trying 2-10 clusters here:
library(cluster)
clusGap(d, kmeans, 10, B = 100, verbose = interactive())
-----------------------------------------------------------------------
7. You may also find it useful to explore your data with clustergrams to visualize cluster 
assignment, see http://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/&nbsp; 
for more details.
-------------------------------------------------------------------
#8. The NbClust package  provides 30 indices to determine the number of clusters in a dataset.
library(NbClust)
nb <- NbClust(d, diss = NULL, distance = "euclidean", 
        min.nc=2, max.nc=15, method = "kmeans", 
        index = "alllong", alphaBeale = 0.1)
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))
# Looks like 3 is the most frequently determined number of clusters
# and curiously, four clusters is not in the output at all!
-----------------------------------------
Here are a few examples:
d_dist <- dist(as.matrix(d))   # find distance matrix 
plot(hclust(d_dist))           # apply hirarchical clustering and plot
----------------------------------------------------
#9 Bayesian clustering method, good for high-dimension data, more details:
# http://vahid.probstat.ca/paper/2012-bclust.pdf
install.packages("bclust")
library(bclust)
x <- as.matrix(d)
d.bclus <- bclust(x, transformed.par = c(0, -50, log(16), 0, 0, 0))
viplot(imp(d.bclus)$var); 
plot(d.bclus); 
ditplot(d.bclus)
dptplot(d.bclus, scale = 20, horizbar.plot = TRUE,varimp = imp(d.bclus)$var, horizbar.distance = 0, dendrogram.lwd = 2)
-------------------------------------------------------------------------
#10 Also for high-dimension data is the pvclust library which calculates 
#p-values for hierarchical clustering via multiscale bootstrap resampling. Here's #the example from the documentation (wont work on such low dimensional data as in #my example):
library(pvclust)
library(MASS)
data(Boston)
boston.pv <- pvclust(Boston)
plot(boston.pv)
------------------------------------
###Automatically cut the dendrogram
require(dynamicTreeCut)
ct_issues <- cutreeHybrid(hc_issues, inverse_cc_combined, minClusterSize=5)
-----
FANNY <- fanny(as.dist(inverse_cc_combined),, k = 3, maxit = 2000) 
FANNY$membership MDS <- smacofSym(distMat)$conf 
plot(MDS, type = "n") text(MDS, label = rownames(MDS), col = rgb((FANNY$membership)^(1/1)))
-----
m7 <- stepFlexmix
----------------------
#11 "clusterSim" -Department of Econometrics and Computer Science, University of #Economics, Wroclaw, Poland
http://keii.ue.wroc.pl/clusterSim
See file ../doc/clusterSim_details.pdf for further details
data.Normalization Types of variable (column) and object (row) normalization formulas
Description
Types of variable (column) and object (row) normalization formulas
Usage
data.Normalization (x,type="n0",normalization="column")
Arguments
x vector, matrix or dataset
type type of normalization: n0 - without normalization
n1 - standardization ((x-mean)/sd)
n2 - positional standardization ((x-median)/mad)
n3 - unitization ((x-mean)/range)
n3a - positional unitization ((x-median)/range)
n4 - unitization with zero minimum ((x-min)/range)
n5 - normalization in range <-1,1> ((x-mean)/max(abs(x-mean)))
n5a - positional normalization in range <-1,1> ((x-median)/max(abs(x-median)))
n6 - quotient transformation (x/sd)
n6a - positional quotient transformation (x/mad)
n7 - quotient transformation (x/range)
n8 - quotient transformation (x/max)
n9 - quotient transformation (x/mean)
n9a - positional quotient transformation (x/median)
n10 - quotient transformation (x/sum)
n11 - quotient transformation (x/sqrt(SSQ))
normalization "column" - normalization by variable, "row" - normalization by objec
See file ../doc/HINoVMod_details.pdf for further details


Nel prossimo post i calcoli con i miei dati

 

Il numero ottimale di cluster può essere determinato da diversi pacchetti e utilizzando più di 30 criteri di ottimizzazione. Secondo le mie osservazioni, il criterio più utilizzato è il criterio di Calinsky.

Prendiamo i dati grezzi del nostro set dall'indicatore dt . Esso contiene 17 predittori, il target y e il corpo della candela z.

Nelle ultime versioni dei pacchetti "magrittr" e "dplyr" ci sono molte nuove funzionalità, una delle quali è la "pipe" - %>%. È molto comodo quando non è necessario salvare i risultati intermedi. Prepariamo i dati iniziali per il clustering. Prendiamo la matrice iniziale dt, selezioniamo le ultime 1000 righe e poi selezioniamo le 17 colonne delle nostre variabili. Otteniamo una notazione più chiara, niente di più.

> library(magrittr)
> x<-dt %>% tail( .,1000)%>% extract( ,1:17)

1.

> library(fpc)
> pamk.best <- pamk(x)
> cat("number of clusters estimated by optimum average silhouette width:", pamk.best$nc, "\n")
> number of clusters estimated by optimum average silhouette width: h: 2

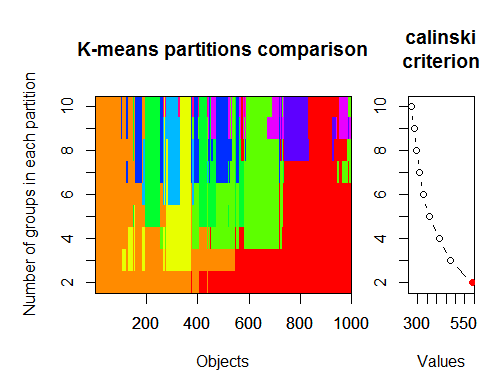
2. Criterio di Calinsky: un altro approccio per diagnosticare quanti cluster sono adatti ai dati. In questo caso

proviamo da 1 a 10 gruppi.

> require(vegan)
> fit <- cascadeKM(scale(x, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
> plot(fit, sortg = TRUE, grpmts.plot = TRUE)

> calinski.best <- as.numeric(which.max(fit$results[2,]))
> cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
Calinski criterion optimal number of clusters: 2
3. Determinare il modello ottimale e il numero di cluster in base al Criterio di informazione bayesiano per la massimizzazione dell'aspettativa, inizializzato dal clustering gerarchico per i modelli a miscela gaussiana parametrizzati.

Modelli a miscela gaussiana 

> library(mclust)
#  Run the function to see how many clusters
#  it finds to be optimal, set it to search for
#  at least 1 model and up 20.
> d_clust <- Mclust(as.matrix(x), G=1:20)
> m.best <- dim(d_clust$z)[2]
> cat("model-based optimal number of clusters:", m.best, "\n")
model-based optimal number of clusters: 7
123456789...17
Nuovo commento