Discussion de l'article "Combinatoire et théorie des probabilités pour le trading (Partie II) : Fractale universelle"
Si cela est possible, je demande à l'auteur de cet article de prendre en considération les arguments suivants :
Jusqu'à présent, je vois que le principe du nombre d'or peut être utilisé pour construire des chaînes fractales-probabilistes formant un groupe complet d'événements, mais honnêtement, je ne vois pas ce qu'une telle approche peut donner. Il semble que le nombre d'or soit également lié à la série fibrée, mais là encore, je ne vois pas comment il peut être appliqué et pour quoi, si vous avez des idées que vous pouvez écrire ici, je pense que ce sera un plus ici. En général, ces processus sont déjà formés dans ma tête, et c'est tout ce qu'il faut pour dériver des formules plus complexes. Jusqu'à présent, les fractales obtenues remplissent leur mission. Ici, tout va du complexe au simple, et ainsi de suite. Je peux penser à l'application du nombre d'or, mais je ne vois pas en quoi cela peut être utile. Les séries Fibo aussi, tout le monde dit fibo-fibo ... Ololo, ils entendent un mot intelligent et le répètent comme un perroquet. Je pars toujours du fait qu'un principe mathématique correspond à un problème particulier, et je trouve toujours une solution à n'importe quel problème après un certain temps. L'outil de la solution est sélectionné au cours du processus, le cerveau le trouve lui-même et, si possible, trouve des similitudes avec quelque chose qui se trouve dans l'oreille. En d'autres termes, nous déterminons d'abord ce que nous devons trouver, puis nous cherchons des moyens de résoudre le problème. Je serais plus intéressé d'entendre des problèmes spécifiques, et vous pouvez faire un article séparé avec de telles solutions, ce serait intéressant et amusant je pense. Dans le cadre de ces problèmes, nous pouvons appliquer le nombre d'or et n'importe quoi d'autre, tant que le résultat est vraiment nécessaire et apporte un avantage concret à quelqu'un. Vous pouvez donc faire des suggestions.
Si cela est possible, je demande à l'auteur de cet article de prendre en considération les arguments suivants :
Ce n'est qu'un mythe éculé de prétendus fibo et ZS partout....
Ce qui est amusant, c'est que si l'on prend n'importe quel pot et qu'on le tourne bien, on peut y trouver à la fois le fibo et le nombre d'or, pi et e et bien d'autres choses....
Ce n'est qu'un mythe éculé de supposés fibo et ZS partout et n'importe où...
Ce qui est drôle, c'est que si on prend n'importe quel pot et qu'on le tourne bien, on peut y trouver le fibo, le nombre d'or, le nombre de pi, le nombre de e et bien d'autres choses....
La fiba (c'est aussi le nombre d'or, ce que beaucoup de gens ne réalisent pas) se cherche, c'est-à-dire se voit, extrêmement facilement. Parce qu'il s'agit d'exponentielles. Qui à leur tour sont des sommes...En général, on peut raconter très longtemps des choses élémentaires de l'école ( !!!) mais ça ne sert à rien.
On peut aussi le faire comme ça :
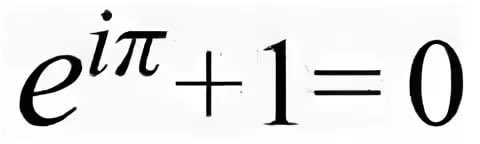
beau, mystérieux...le lien de FIBO avec Fourier...les constantes du monde dans un verre...et d'autres trucs.
Ce n'est qu'un mythe éculé de supposés fibo et ZS partout et n'importe où...
Le plus drôle, c'est que si on prend n'importe quel pot et qu'on le fait bien tourner, on peut y trouver le fibo et le nombre d'or et le nombre de pi et le nombre de e et bien d'autres choses....
vous pouvez aussi trouver la tête et les épaules dans le pot si vous le mettez sur votre tête).
C'est juste un mythe éculé que Fibo et ZS sont partout et partout....
Ce qui est amusant, c'est que si l'on prend n'importe quel pot et qu'on le tourne bien, on peut y trouver la fibo, le nombre d'or, pi, e et bien d'autres choses....
Je suis tout à fait d'accord )) c'est vraiment vrai. Les traders aiment beaucoup chercher un sens caché là où il n'y en a pas du tout ). J'essaie de faire comprendre la même chose aux gens, mais je ne sais pas comment le faire sans dire la vérité, et la vérité est cruelle ). J'en suis arrivé à la conclusion qu'il y a un problème et un ensemble de solutions possibles, et que tout le reste est une perte de temps. Pour obtenir une solution, il faut d'abord poser clairement le problème et avoir au moins une idée superficielle des voies possibles de sa solution, s'il n'y en a pas, alors commence ce qui précède, Fibonacci, les formules d'Euler et autres stupidités très belles mais tellement inutiles que l'on se met involontairement à lire entre les lignes. Chaque outil a sa propre tâche. Dans ce contexte, je vous propose d'entrer dans le concret (les tâches concrètes).
Jusqu'à présent, je vois que le principe du nombre d'or peut être utilisé pour construire des chaînes de probabilité fractales qui forment un groupe complet d'événements, mais honnêtement, je ne vois pas ce que cette approche peut faire. Il semble que le nombre d'or soit également lié aux séries fibrées, mais là encore, je ne vois pas comment il peut être appliqué et si vous avez des idées que vous pouvez écrire ici, je pense que ce sera un plus. En général, ces processus sont déjà formés dans ma tête, et c'est tout ce qu'il faut pour dériver des formules plus complexes. Jusqu'à présent, les fractales obtenues remplissent leur mission. Ici, tout va du complexe au simple, et ainsi de suite. Je peux penser à l'application du nombre d'or, mais je ne vois pas en quoi cela peut être utile. Les séries Fibo aussi, tout le monde dit fibo-fibo ... Ololo, ils entendent un mot intelligent et le répètent comme un perroquet. Je pars toujours du fait qu'un principe mathématique correspond à un problème particulier, et je trouve toujours une solution à n'importe quel problème après un certain temps. L'outil de la solution est sélectionné au cours du processus, le cerveau le trouve lui-même et, si possible, trouve des similitudes avec quelque chose qui se trouve dans l'oreille. En d'autres termes, nous déterminons d'abord ce que nous devons trouver, puis nous cherchons des moyens de résoudre le problème. Je serais plus intéressé d'entendre des problèmes spécifiques, et vous pouvez faire un article séparé avec de telles solutions, ce serait intéressant et amusant je pense. Dans le cadre de ces problèmes, nous pouvons appliquer le nombre d'or et n'importe quoi d'autre, tant que le résultat est vraiment nécessaire et apporte un avantage concret à quelqu'un. Vous pouvez donc écrire des suggestions.
1. Peut-être que tout le monde a entendu parler de cet "ololo", mais je n'ai pas écrit sur le fibo, parce que je ne conseille pas de "tirer" les niveaux de fibo, bien que s'ils sont calculés correctement, ils peuvent être utilisés, mais en combinaison avec les vagues d'Elliott.
Bien sûr, ce n'est pas tout, vous vous rendez compte à quel point ce travail est long et fastidieux, mais j'ai commencé ce fil de discussion pour une raison. J'essaierai de faire tout ce qui dépend de moi, et en général, pour être honnête, de telles questions devraient être traitées par une équipe entière de mathématiciens et de programmeurs, voire par un institut entier. Que peut faire une seule personne contre cela ? Même si vous avez un super cerveau, il y a tellement de données à traiter que vous pouvez devenir fou. J'essaie de me fixer des tâches qui correspondent à mon temps et à mes capacités, oui je peux en faire plus, mais cela ne dépend pas de moi maintenant. Le temps est la ressource la plus précieuse. S'il y a des personnes intéressées par des analyses complexes et un dévouement total, je serais heureux de le faire. Néanmoins, la branche continuera et je couvrirai le matériel que je peux, j'essaie toujours d'apporter quelque chose de nouveau, dans la mesure du possible.
Le mythe de l'universalité du nombre d'or dans la nature s'est tellement développé que les gens ne s'embarrassent même pas de vérifications réelles, succombant aux charmes de la beauté de l'idée même du rapport entre le tout et ses parties, mais en fait il n'en est rien :
- les coquilles de mollusques-nautilus (qui sont généralement illustrées dans les articles sur la magie de la DT), contrairement à l'opinion générale, ne correspondent pas à la DT.
- Les proportions d'un corps humain tirées du célèbre dessin de Léonard de Vinci "L'homme de Vitruve" ne sont pas observées par rapport à des personnes réelles.
- Le Parthénon, les pyramides et d'autres objets correspondent de manière très imprécise à RS (dessinés par des amateurs de mysticisme).
- Les recherches psychologiques objectives visant à déterminer si le QE est à la base de la perception de la beauté ont échoué avec succès.
- Enfin, les tests quantitatifs de rupture/rejet de niveaux dans le commerce ne montrent pas non plus que le QE est quelque chose de particulièrement important.
La seule raison pour laquelle les marchés peuvent parfois (mot-clé : UNE AUTRE FOIS) bien remonter les niveaux de fibrage est la croyance collective d'un grand nombre de traders techniques dans les niveaux de fibrage (une prophétie qui se réalise d'elle-même) s'ils placent collectivement leurs stops/limites à cet endroit, mais même cela ne fonctionnera probablement pas parce que les participants professionnels, les grands acteurs institutionnels négocieront sur une autre base, et l'effondrement/le renversement du niveau Fibo pourrait n'être qu'un hasard, mais pour les personnes qui croient au QE, il s'agira certainement d'une confirmation de leur foi.
Keith Devlin, professeur de mathématiques à l'université de Stanford, l'explique simplement : "..... La plupart des gens ne comprennent pas les mathématiques et ne peuvent même pas comprendre comment une formule comme le nombre d'or s'applique à un système complexe. Les gens croient voir le nombre d'or partout, dans la nature et dans leurs objets préférés, mais ils ne peuvent pas le prouver. Ils sont victimes de leur désir naturel de trouver un sens aux divers objets de l'univers, mais leur manque de culture mathématique les empêche de réaliser que les modèles qu'ils détectent sont illusoires".
Les gens se programment (zombie) pour trouver une explication simple et s'efforcent de maintenir cette croyance, c'est l'essence même de la pensée religieuse, y compris dans le commerce...
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Un nouvel article Combinatoire et théorie des probabilités pour le trading (Partie II) : Fractale universelle a été publié :
Dans cet article, nous poursuivrons l'étude des fractales et nous nous attacherons à résumer l'ensemble du matériel. Pour ce faire, j'essaierai de rassembler tous les développements antérieurs sous une forme compacte, pratique et compréhensible pour une application pratique dans le domaine du trading.
Utilisons les règles de construction que nous avons dérivées dans l'article précédent, et complétons-les pour comprendre comment une fractale est construite. J'ai également trouvé une petite erreur dans mes formules, à cause de laquelle l'asymétrie des frontières vers le bas ou vers le haut était impossible. Les formules dérivées se sont avérées correctes et fonctionnent donc pour n'importe quelle fractale. En fait, il s'agit d'une fonction permettant d'implémenter n'importe quelle fractale. Toutes les fractales possibles sont un cas particulier d'une fractale générale. Si nous prenons les trois types de fractales définis ci-dessus, les conditions de la fractale générale pour la mise en œuvre de ces 3 cas particuliers seront les suivantes :
Schématiquement, ces 3 types de fractales se présentent comme suit :
Idéalement, "S" devrait tendre vers l'infini. Les variables suivantes n'ont pas été décrites dans mon article précédent. Je fournirai ici les descriptions afin d'obtenir une image complète de la manière d'utiliser la formule générale pour obtenir les cas particuliers. Une fractale est une fonction qui fonctionne sur le principe d'une réaction en chaîne, comme dans une bombe atomique. Si la réaction en chaîne est trop profonde, l'ordinateur risque de ne pas pouvoir faire face à des calculs aussi importants. Si le cas n'est pas particulièrement critique, elle prendra simplement un temps très long - des minutes, des heures, voire des jours.
Auteur : Evgeniy Ilin