Implementing NSGA-II with Complex Constraints in Strategy Tester

New comment
 

Hello everyone,

I'm working on optimizing a trading strategy using the Strategy Tester in MetaTrader, and I'm facing some challenges implementing a custom multi-objective optimization algorithm (NSGA-II) due to complex constraints.

Specifically, my model has several constraints that make it unsuitable for the standard genetic algorithm optimizer. For example, consider three input parameters (a, b, c) of type double with the following constraints:

  1. a + b + c = 1
  2. a >= b
  3. if (c > 0.7) then a = 0

My objective functions are:

  1. Maximize Balance
  2. Maximize Win Rate
  3. Minimize Balance Drawdown Percentage
  4. Maximize Profit Factor
  5. Maximize Recovery Factor
  6. Maximize Sharpe Ratio

Has anyone had experience implementing custom metaheuristic algorithms, particularly NSGA-II, within the Strategy Tester environment, especially when dealing with such constraints? I'm looking for any insights or "heads-up" regarding:

  • Best practices for integrating custom optimization algorithms.
  • Efficient ways to handle complex constraints within the Strategy Tester.
  • Potential pitfalls or limitations to be aware of.
  • Any example code or resources that might be helpful.

Any advice or guidance would be greatly appreciated!

Thanks in advance.

 
Mobin Zarekar:

Hello everyone,

I'm working on optimizing a trading strategy using the Strategy Tester in MetaTrader, and I'm facing some challenges implementing a custom multi-objective optimization algorithm (NSGA-II) due to complex constraints.

Specifically, my model has several constraints that make it unsuitable for the standard genetic algorithm optimizer. For example, consider three input parameters (a, b, c) of type double with the following constraints:

  1. a + b + c = 1
  2. a >= b
  3. if (c > 0.7) then a = 0

My objective functions are:

  1. Maximize Balance
  2. Maximize Win Rate
  3. Minimize Balance Drawdown Percentage
  4. Maximize Profit Factor
  5. Maximize Recovery Factor
  6. Maximize Sharpe Ratio

Has anyone had experience implementing custom metaheuristic algorithms, particularly NSGA-II, within the Strategy Tester environment, especially when dealing with such constraints? I'm looking for any insights or "heads-up" regarding:

  • Best practices for integrating custom optimization algorithms.
  • Efficient ways to handle complex constraints within the Strategy Tester.
  • Potential pitfalls or limitations to be aware of.
  • Any example code or resources that might be helpful.

Any advice or guidance would be greatly appreciated!

Thanks in advance.

Hi

Is the test pass rejected when any of the constraints are broken ?

 
Lorentzos Roussos #:

Hi

Is the test pass rejected when any of the constraints are broken ?

Hi,

Yes, we must reject a test pass when any of the conditions are not valid. However, we need to maintain a robust algorithm to generate random numbers that satisfy the constraints.

For example, if we have three double-precision numbers constrained by the condition that their sum equals 1, and we require five-digit accuracy, generating completely random numbers that meet this condition may take many iterations. The default optimizer in MT5 handles this efficiently using a genetic algorithm (of course, with structured steps).

Corrected Approach for Generating Feasible Numbers

A well-structured method to generate three numbers a , b , and c such that their sum equals 1 is the stick-breaking method, which ensures uniform distribution:

double a, b, c; double x1 = RandomDouble(0, 1); double x2 = RandomDouble(0, 1); if (x1 > x2) Swap(x1, x2); // Ensure x1 <= x2 a = x1; b = x2 - x1; c = 1 - x2;

Explanation of the Approach:

  1. Generate two random numbers x1 and x2 independently between 0 and 1.

  2. Sort them so that x1 ≤ x2 . This ensures correct partitioning of the unit interval.

  3. Assign values based on their positions in the sorted sequence:

    • a = x1

    • b = x2 - x1

    • c = 1 - x2

With this approach, we generate feasible answers while ensuring a uniform distribution across all valid (a, b, c) triplets. 🚀

 
Mobin Zarekar #:

Hi,

Yes, we must reject a test pass when any of the conditions are not valid. However, we need to maintain a robust algorithm to generate random numbers that satisfy the constraints.

For example, if we have three double-precision numbers constrained by the condition that their sum equals 1, and we require five-digit accuracy, generating completely random numbers that meet this condition may take many iterations. The default optimizer in MT5 handles this efficiently using a genetic algorithm (of course, with structured steps).

Corrected Approach for Generating Feasible Numbers

A well-structured method to generate three numbers a , b , and c such that their sum equals 1 is the stick-breaking method, which ensures uniform distribution:

double a, b, c; double x1 = RandomDouble(0, 1); double x2 = RandomDouble(0, 1); if (x1 > x2) Swap(x1, x2); // Ensure x1 <= x2 a = x1; b = x2 - x1; c = 1 - x2;

Explanation of the Approach:

  1. Generate two random numbers x1 and x2 independently between 0 and 1.

  2. Sort them so that x1 ≤ x2 . This ensures correct partitioning of the unit interval.

  3. Assign values based on their positions in the sorted sequence:

    • a = x1

    • b = x2 - x1

    • c = 1 - x2

With this approach, we generate feasible answers while ensuring a uniform distribution across all valid (a, b, c) triplets. 🚀

Ow you mean how the optimizer creates useless passes .

what if b is % of 1-a and c is just calculated resulting from the other 2 ?

 

It can be done as long as calculations perform like dominos.

this is the mathematical model sample :

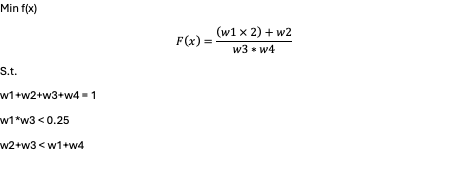
our inputs are w1,...,w4

We want to minimize f ( x ) f(x)  while satisfying the following constraints on our inputs.

For example, to satisfy the first constraint, if we try to generate four random numbers whose sum is exactly 1, it would require significant computational resources. We need to develop methods to handle the generation of new genes (new parameters for answers).

 
Lorentzos Roussos #:

Ow you mean how the optimizer creates useless passes .

what if b is % of 1-a and c is just calculated resulting from the other 2 ?

I forget to Tag you in my answer :))

 
Mobin Zarekar #:

It can be done as long as calculations perform like dominos.

this is the mathematical model sample :

our inputs are w1,...,w4

We want to minimize f ( x ) f(x)  while satisfying the following constraints on our inputs.

For example, to satisfy the first constraint, if we try to generate four random numbers whose sum is exactly 1, it would require significant computational resources. We need to develop methods to handle the generation of new genes (new parameters for answers).

are these weights ?

(no)

this is the formula for the criterion

If your constraints are for the formula too , penalize the score when they are violated.

I'd set the score to INT_MIN but that creates 2 problems :

1. you cant see the project scale

2. the solution is not "walkable"

 

I propose a solution to address the issue that MQL5's strategy tester does not support relative input parameter adjustments. We need a workaround to enforce constraints on input parameters.

Consider a simple case: we have two inputs, A and B, which must sum to 10, with both ranging from 1 to 9. Since the strategy tester cannot directly enforce this constraint during input step changes, we can create a combination vector listing all valid pairs of A and B that satisfy the sum:

  • Pack 0: A = 9, B = 1
  • Pack 1: A = 8, B = 2
  • ...
  • Pack 8: A = 1, B = 9

Instead of using A and B as inputs, we define a single integer input to select the pack:


input int pack_index = 0;

During optimization, we increment pack_index from 0 to 8 in steps of 1 to iterate through all valid combinations.

For larger problems, such as 50 variables summing to 1000, storing all combinations is memory-intensive. Instead, we can implement a method to dynamically calculate and return only the specific combination needed based on the index, avoiding excessive memory usage.// Calculates the binomial coefficient C(a, b)

   long binomial(int a, int b) {
        if (b > a || b < 0) return 0;
        if (b > a - b) b = a - b; // Optimize by using symmetry
        long result = 1;
        for (int i = 1; i <= b; i++) {
            result *= (a - b + i);
            result /= i;
        }
        return result;
    }

    // Generates all combinations of k integers summing to 100
    void generate_combinations(int k, int& combination[], int stride) {
        long num_combs = binomial(100 + k - 1, k - 1); // Number of combinations
        ArrayResize(combination, (int)(num_combs * stride)); // Resize array, cast to int to avoid warning
        int index = 0;
        int current[];
        ArrayResize(current, k); // Temporary array to hold current combination
        fill_combinations(k, 100, current, 0, combination, index, stride);
    }
New comment