I have code a LSR function based off of https://techimperialist.com/ai-ml/a-simple-introduction-to-linear-regression-the-least-square-method/
Output
Now, using the same values for input in google docs the results are very different
According to the Docs, the formula uses the least square method.
Why is there a huge difference? Is my code missing a processing step of some sorts? Unfortunately math is my weakest link so maybe a Math wizzard could help me in the right direction.
In LINEST , you have sent the axis inverse to the way you did on your code .
Try LINEST(H4:H6,D4:D6,1,0) its the same
The order in my code and on google docs is the same. {edit, i see what you mean, LINEST input is y,x. Mine x,y}
If i reverse the order in docs as per your suggestion, it does not match either.
Indeed, then it is the same.
Is it not strange the slope coefficient becomes different with the calculate_b flag set true instead of false? Or am i missing something (again)?
Indeed, then it is the same.
Is it not strange the slope coefficient becomes different with the calculate_b flag set true instead of false? Or am i missing something (again)?
i guess that's what they mean with " i.e. forces the curve fit to pass through the origin." although i don't understand how they alter the calculation for that.
I guess that explains it indeed.
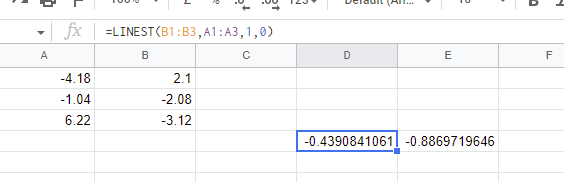
On your screenshot i notice the -0.88.. number, is this output from LINEST or did you use another function to calculate it?
If i put the Verbose flag to false, it prints no Intercept, and if i set to true i get another intercept number
I guess that explains it indeed.
On your screenshot i notice the -0.88.. number, is this output from LINEST or did you use another function to calculate it?
If i put the Verbose flag to false, it prints no Intercept, and if i set to true i get another intercept number
Actually , what i said was stupid sorry , what they mean is if you return no intercept then ofcourse the slope goes through the origin .
the -0.88 is the intercept , that is how the linest prints , i just picked one cell .
Your 0.274 value is not the intercept , its the The standard error value for the slope
Clear. Thanks so much for helping!
{edit Correct, i miss-labeled which lead to my confusion. It is indeed the standard error.}
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
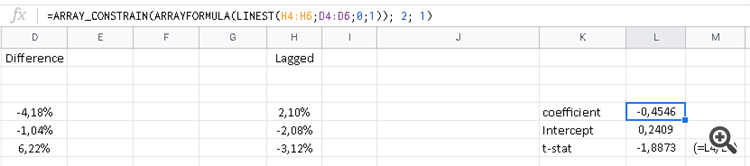


I have code a LSR function based off of https://techimperialist.com/ai-ml/a-simple-introduction-to-linear-regression-the-least-square-method/
Output
Now, using the same values for input in google docs the results are very different
According to the Docs, the formula uses the least square method.
Why is there a huge difference? Is my code missing a processing step of some sorts? Unfortunately math is my weakest link so maybe a Math wizzard could help me in the right direction.