[Archive!] Pure mathematics, physics, chemistry, etc.: brain-training problems not related to trade in any way - page 614

New comment
 
Mathemat:

Dima, why do you want to know the probability that differs from one by thousandths of a percent? If you want guarantees, there are none. Nobel Laureates (LTCM) and Niederhoffer himself hid behind probabilities to some degree minus one - and still "hit".

By thousandths of a percent - not necessary. But 120 transactions is a lot, it should be possible to calculate for a small number of transactions, for example - for 20, 30, 40. And 30% is not enough for 120.

And very small probabilities (very large) are used to calculate the approximate lifetime of the system. It is important to know how long it will last - a year or 10 years.
Is there something to rely on? Mathematics is the best way to go.
 
Well, at least read up on some basic terw, it'll come in handy anyway.
 
GaryKa, Mathemat

Right?



 
DmitriyN: Right?

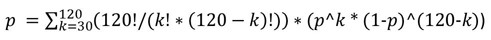
That's right!

But rounding errors can eat up all the accuracy. It's better to count the sum from 0 to 30. It will be equal to the addition to the probability you want to know.

 
If balls are returned, then always p=q, so we can simplify the formula in the right-hand side (* p^120)
 
Mislaid: We solve the problem cardinally: no equality. Determine that the sets of numbers on the faces of the cube should not overlap.

There are cases, there are cases where the sum of the faces equals 17.

For example, (333332) > (662111), with a probability of winning of 23/36 ~ 0.64. True, it is not simple there: (662111) does not win by any appreciable margin.

It seems that so far the sum of the faces of 18 is the most fertile.

 
GaryKa:
If we return the balls, then it is always p=q, so we can simplify the formula in the right hand side (* p^120)

It doesn't really matter if we return or not. We extract too little to make any difference. But it can be simplified decently. And in brackets with powers the multiplier (1/2)^120 will remain.

Hehe.

2 Dima: Don't bother with these combinations. Get a handle on the normal distribution and take a definite integral from zero to the lower bound corresponding to your 30. You will make a big mistake with combinations in this formula, unless you find an analytical formula for the simple sum of combinations.

Or try the sum of combinations from 0 to 30, the p grades won't bother you. You might get lucky.

P.S. In short, it's simple. Look here.

You need to calculate k1, k2 and then the integral.

Let's take k1=0, k2=30, this is more accurate. n=120, p=q=1/2. Then

(k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477

(k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10.954.

Also 1/sqrt(2*pi) ~ 0.39894 comes in handy.

Substitute the first two numbers in the integration limits, and substitute 0.39894*exp(-x^2/2) into the integrand function, and we obtain ( here is a service on taking certain integrals):

2.163*10^(-8).

So your probability is 1-2.163*10^(-8) ~ 0.99999998.

Don't even try to take the initial of the function under the integral: it is non-integer.

 
Mathemat: ... Work out the normal distribution ... unless you can find an analytical formula for a simple sum of combinations ...
These words of yours gave me an interesting idea to try to find an analytical formula for calculating a combination through a normal distribution ))
 
Mathemat:
I'll try to figure it out. Good links.
 
GaryKa: These words of yours have given me an interesting idea - to try to find an analytical formula for calculating the combination through a normal distribution ))
Well that is the local Moab-Laplace theorem.
1...607608609610611612613614615616617618619620621...628
New comment
Reason: