文章 "您应该知道的 MQL5 向导技术（第 02 部分）：Kohonen 映射"
剩下的一个问题是，我们如何理解为什么 IN_RADIUS 的值被用来对数据进行标准化处理：
double _dimension=fabs(IN_RADIUS)*((Low(StartIndex()+w+Index)-Low(StartIndex()+w+Index+1))-(High(StartIndex()+w+Index)-High(StartIndex()+w+Index+1))))/fmax(m_symbol.Point(),fmax(High(StartIndex()+w+Index),High(StartIndex()+w+Index+1))-fmin(Low(StartIndex()+w+Index),Low(StartIndex()+w+Index+1))))；
因为簇半径是一个常数，并且是正值。
也许这是一个错误，整个分母应该取模？
我组装了 Expert Advisor，但止损和获利这两个参数与文章截图上的不一样：
结果，没有一笔交易...
我是不是做错了什么？
如何使用其他指标代替 ATR，例如 MACD？
您可以这样做：
bool CSignalMACD::InitMACD(CIndicators *indicators) { //--- 将对象添加到集合中 if(!indicators.Add(GetPointer(m_MACD))) { printf(__FUNCTION__+": error adding object"); return(false); } //--- 初始化对象 if(!m_MACD.Create(m_symbol.Name(),m_period,m_period_fast,m_period_slow,m_period_signal,m_applied)) { printf(__FUNCTION__+": error initializing object"); return(false); } //--- ok return(true); }
也可以在受保护状态下
protected: CiMACD m_MACD; // 对象振荡器 //-- 调整参数 int m_period_fast; // 振荡器的 "快速 EMA 周期 "参数 int m_period_slow; // 振荡器的 "慢速 EMA 周期 "参数 int m_period_signal; // 振荡器的 "差值平均周期 "参数 ENUM_APPLIED_PRICE m_applied; // 摆动器的 "价格序列 "参数
和公开
void PeriodFast(int value) { m_period_fast=value; } void PeriodSlow(int value) { m_period_slow=value; } void PeriodSignal(int value) { m_period_signal=value; } void Applied(ENUM_APPLIED_PRICE value) { m_applied=value;
再在受保护 状态下
protected: //--- 振荡器的初始化方法 bool InitMACD(CIndicators *indicators); //--- 获取数据的方法 double Main(int ind) { return(m_MACD.Main(ind)); } double Signal(int ind) { return(m_MACD.Signal(ind)); }
最后
bool CSignalKM::OpenLongParams(double &price,double &sl,double &tp,datetime &expiration) { CExpertSignal *general=(m_general!=-1) ? m_filters.At(m_general) : NULL; //--- if(general==NULL) { m_MACD.Refresh(-1); //--- 如果没有明确指定基准价格，则采用当前市场价格 double base_price=(m_base_price==0.0) ? m_symbol.Ask() : m_base_price; //--- 价格重载，根据 MACD 设置入口价格 price =base_price; double _range=m_MACD.Main(StartIndex())+((m_symbol.StopsLevel()+m_symbol.FreezeLevel())*m_symbol.Point()); //
但有什么意义呢？
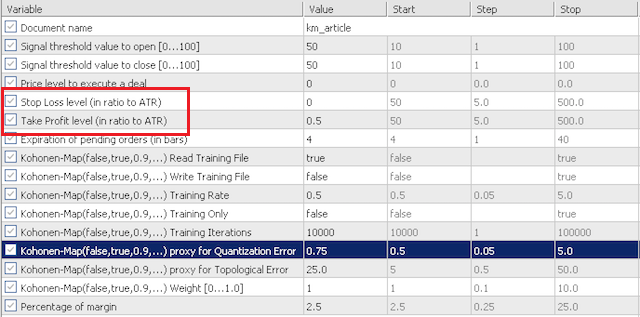
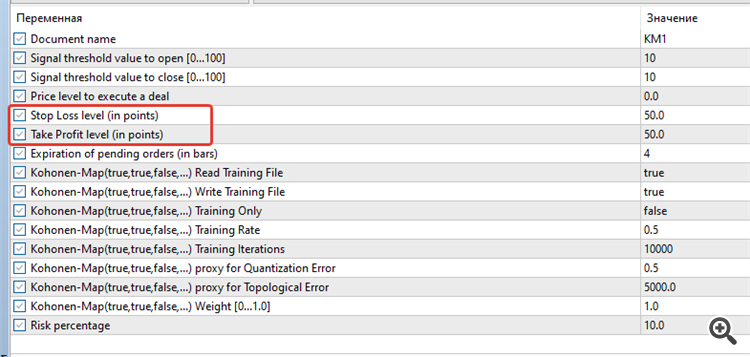
新文章 您应该知道的 MQL5 向导技术（第 02 部分）：Kohonen 映射已发布：
这些系列文章所提议的是，MQL5 向导应作为交易员的支柱。 为什么呢？ 因为交易员不仅可以利用 MQL5 向导装配他的新想法来节省时间，还可以大大减少重复编码带来的错误；他最终可把精力投向自我交易哲学中的几个关键领域。
这些映射的一个常见误解是 functor 数据应该是图像或二维。 下面的图片都是作为 Kohonen 映射的代表而被分享的。
虽然没有错，但我想强调 functor 可以且也许应该（对于交易者）有一个单一维度。 因此，我们不会将高维数据降维到 2D 映射，而是将其映射到一条直线上。根据定义，Kohonen 映射旨在降低维度，因此我希望我们将这一点带到本文的下一个层面。kohonen 映射在层数和底层算法上都不同于常规神经网络。 它是神经元的单层（通常是前面提到的线性 2D 网格）集合，取代了多层。 这一层上的所有神经元，即我们正在参考的 functor 都与 feed 连接，但不是它们自身，这意味着神经元不受彼此权重的直接影响，且只随 feed 层面数据更新。functor 数据层通常是一个“映射”，它根据 feed 数据在每次训练迭代中组织自己。由此，训练之后，每个神经元在 functor 层中都有权重调整维度，这令我们可以计算任意两个这样的神经元之间的 Euclidean 距离。
作者：Stephen Njuki