关于钱币 - 页 6 12345678910111213...16 新评论 Igor Makanu 2021.05.30 11:45 #51 CHINGIZ MUSTAFAEV: 你不会相信,但即使是随机性也有一个模式。这就是所谓的大数法则。 noooo....这是旧的,"较新 "的是 "计算等价原则"。 Andrei Trukhanovich 2021.05.30 11:52 #52 感觉这个论坛正在迅速恶化。 一方面,这是好的--在交易中拥有肉类是必不可少的。另一方面,很快就没有人可以说话了 denis.eremin 2021.05.30 12:04 #53 Andrei Trukhanovich:感觉这个论坛正在迅速恶化。一方面,这是好的--在交易中拥有肉类是必不可少的。另一方面,很快就没有人可以聊天了。 这个论坛正在迅速退化,因为所有的话题都已经讨论了很多年了。 Andrei Trukhanovich 2021.05.30 12:21 #54 denis.eremin:...多年来,所有的主题都已涵盖。 胡说八道)这样的观点可能表明你也是退化人群的一部分。 apr73 2021.05.30 13:02 #55 denis.eremin: 我最后解释一下--随机漫步是一个数字序列,根据定义,其中 没有规律和秩序。根本就没有。所以你只能靠它来赚钱。CHINGIZ MUSTAFAFAEV: 你不会相信,但即使是机会也有模式。这被称为大数法则。 的确,有,人们说没有这样的模式。 "大数法则"。 大数法则广义的,指的是这样的一般原则:当 大量的随机变量时,它们的平均 结果就不再是随机的,可以高度肯定地。" 或者像这样 "大数法则"。 大量随机因素的累积效应导致。 "在某些一般条件下,一个几乎与机会无关的结果。 即具有系统性的"。 Dmitry Fedoseev 2021.05.30 13:12 #56 apr73:确实有,人们说没有模式。"大数法则广义的大数法则,指的是这样的一般原则:当 大量的随机变量时,它们的平均 结果就不再是随机的,可以高度肯定地预测"。或者像这样"大量随机因素的累积效应导致。 "在某些一般条件下,一个几乎与机会无关的结果。 即具有系统性的"。XXX网站 旨在为你提供良好的建议并帮助你学习...是的))。 CHINGIZ MUSTAFAEV 2021.05.30 13:12 #57 Igor Makanu:noooo....这是旧的,"新 "的是 "计算等效原则"。 嗯,有意思,我得读一读)。 CHINGIZ MUSTAFAEV 2021.05.30 13:16 #58 denis.eremin:具体实施。再一次,你有完美的硬币,你认为通过投注老鹰,你将获得利润,因为这是你天才的交易策略。你翻了一百次60/40,你就有了钱。再来一百次,51/49,你就有钱了。再来一次,72/18,你就能拿到钱了。你来到表格前,抛出结果并写道--"但这三张利润最明显的直方图呢"? 这里有一个给那些完全 在棕色罐子里的人。 赌的不是你的硬币是正面还是反面,那是没有用的,真的不可能赢,而是在一百次射击的系列中,大约40-45%会是反面,而50-100次的系列中,40-45次会是反面的系列趋于90-95%。 为什么你认为网的作用,它们是相同的投掷,而网的数量是许多投掷的系列=D Alexander_K2 2021.05.30 13:22 #59 CHINGIZ MUSTAFAEV:这里有一个给那些完全是 BORROWN TANK的人。 赌的不是你的硬币是正面还是反面,那是没有用的,真的不能赢,而是在一百次射击的系列中,大约40-45%会是反面,而在50-100次的系列中,40-45次射击会是反面的系列趋于90-95%。 为什么你认为网的作用,它是相同的投掷,网的数量是许多投掷的系列=D 再一次--好样的!!!。不,甚至是--勇敢的人!!!。我说的就是这个系列,它不能被某位博士理解(由于纯粹的未受教育)。 Alexander_K2 2021.05.30 13:28 #60 答案就这样回来了。决定对3000条轨迹进行反复检查......坦率地说,对我来说是一个意想不到的结果,但我倾向于认为我做错了什么。我必须拿着聪明的书仔细检查一切)))。因此,对结果而言: 我们首先评估胜负的分布是否正常,直观地看一下 类似于正常的东西。 测试。Shapiro-Wilk正态性测试W = 0.99894,P值 = 0.06206Anderson-Darling正态性测试A=0.78803,P值=0.04098 在5%的显著性水平上......好哦,几乎是正常的 在1%的水平上--拒绝正态性的无效假设更加有趣)对样本平均值等于零进行单样本t检验。单一样本t检验t = 5.5464, df = 2999, p-值 = 3.17e-08备选假设:真实平均值不等于095%的置信区间。10.74520 22.49687抽样估计。x的平均数16.62104因此,即使在百分之一的置信水平下,平均利润等于零的假设也很容易被拒绝。现在,从结果中删除异常值后也是如此。 Shapiro-Wilk正态性测试W = 0.99781,P值 = 0.0003555Anderson-Darling正态性测试A = 0.70627,P值 = 0.06521单一样本t检验t = 6.1144, df = 2972, p值 = 1.096e-09备选假设:真实平均值不等于095%的置信区间。12.08241 23.48974抽样估计。x的平均数17.78607我们可以看到,仍然不清楚分布是否为正态,但关于平均值的数据更有说服力。结论是什么?我需要仔细检查和认真思考))) About the coin 深度神经网络 (第 II 部)。制定和选择预测因子 12345678910111213...16 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
你不会相信,但即使是随机性也有一个模式。这就是所谓的大数法则。
noooo....这是旧的,"较新 "的是 "计算等价原则"。
感觉这个论坛正在迅速恶化。
一方面,这是好的--在交易中拥有肉类是必不可少的。另一方面,很快就没有人可以说话了
感觉这个论坛正在迅速恶化。
一方面,这是好的--在交易中拥有肉类是必不可少的。另一方面,很快就没有人可以聊天了。
这个论坛正在迅速退化,因为所有的话题都已经讨论了很多年了。
...多年来,所有的主题都已涵盖。
胡说八道)这样的观点可能表明你也是退化人群的一部分。
denis.eremin:我最后解释一下--随机漫步是一个数字序列,根据定义,其中 没有规律和秩序。根本就没有。
所以你只能靠它来赚钱。
CHINGIZ MUSTAFAFAEV:
你不会相信,但即使是机会也有模式。这被称为大数法则。
的确,有,人们说没有这样的模式。
"大数法则"。
大数法则广义的
,指的是这样的一般原则:当
大量的随机变量时,它们的平均
结果就不再是随机的,可以高度肯定地
。"
或者像这样
"大数法则"。
大量随机因素的累积效应导致。
"在某些一般条件下,一个几乎与机会无关的结果。
即具有系统性的"。
确实有,人们说没有模式。
"大数法则
广义的大数法则
,指的是这样的一般原则:当
大量的随机变量时,它们的平均
结果就不再是随机的,可以高度肯定地预测
"。
或者像这样
"大量随机因素的累积效应导致。
"在某些一般条件下,一个几乎与机会无关的结果。
即具有系统性的"。
noooo....这是旧的,"新 "的是 "计算等效原则"。
嗯,有意思,我得读一读)。
具体实施。
再一次,你有完美的硬币,你认为通过投注老鹰,你将获得利润,因为这是你天才的交易策略。
你翻了一百次60/40,你就有了钱。
再来一百次,51/49,你就有钱了。
再来一次,72/18,你就能拿到钱了。
你来到表格前,抛出结果并写道--"但这三张利润最明显的直方图呢"?
这里有一个给那些完全 在棕色罐子里的人。
赌的不是你的硬币是正面还是反面,那是没有用的,真的不可能赢,而是在一百次射击的系列中,大约40-45%会是反面,而50-100次的系列中,40-45次会是反面的系列趋于90-95%。
为什么你认为网的作用,它们是相同的投掷,而网的数量是许多投掷的系列=D
这里有一个给那些完全是 BORROWN TANK的人。
赌的不是你的硬币是正面还是反面,那是没有用的,真的不能赢,而是在一百次射击的系列中,大约40-45%会是反面,而在50-100次的系列中,40-45次射击会是反面的系列趋于90-95%。
为什么你认为网的作用,它是相同的投掷,网的数量是许多投掷的系列=D
再一次--好样的!!!。不,甚至是--勇敢的人!!!。我说的就是这个系列,它不能被某位博士理解(由于纯粹的未受教育)。
答案就这样回来了。
决定对3000条轨迹进行反复检查......坦率地说,对我来说是一个意想不到的结果,但我倾向于认为我做错了什么。我必须拿着聪明的书仔细检查一切)))。
因此,对结果而言:
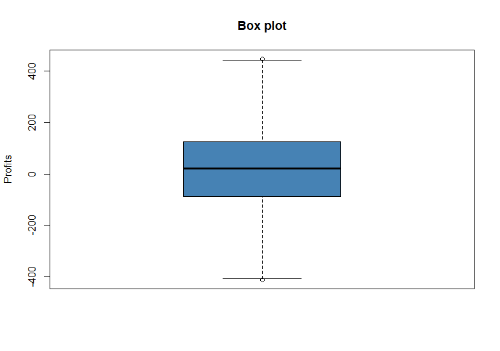
我们首先评估胜负的分布是否正常,直观地看一下
类似于正常的东西。
测试。
Shapiro-Wilk正态性测试
W = 0.99894,P值 = 0.06206
Anderson-Darling正态性测试
A=0.78803,P值=0.04098
在5%的显著性水平上......好哦,几乎是正常的
在1%的水平上--拒绝正态性的无效假设
更加有趣)
对样本平均值等于零进行单样本t检验。
单一样本t检验
t = 5.5464, df = 2999, p-值 = 3.17e-08
备选假设:真实平均值不等于0
95%的置信区间。
10.74520 22.49687
抽样估计。
x的平均数
16.62104
因此,即使在百分之一的置信水平下,平均利润等于零的假设也很容易被拒绝。
现在,从结果中删除异常值后也是如此。
Shapiro-Wilk正态性测试
W = 0.99781,P值 = 0.0003555
Anderson-Darling正态性测试
A = 0.70627,P值 = 0.06521
单一样本t检验
t = 6.1144, df = 2972, p值 = 1.096e-09
备选假设:真实平均值不等于0
95%的置信区间。
12.08241 23.48974
抽样估计。
x的平均数
17.78607
我们可以看到,仍然不清楚分布是否为正态,但关于平均值的数据更有说服力。
结论是什么?我需要仔细检查和认真思考)))