霍德里克-普雷斯科特过滤器
我没有看到muving的滞后性。这意味着作者不了解他所设定的内容，或者算法有误，指标重画。
没有滞后性，因为它不是一般的muwink。解决了给定系列的函数最小化的问题。当然，当序列在移动时，如果序列的长度很小，当新的信息出现时，它会重新绘制，特别是当有尖峰时。滤波器的描述：http://en.wikipedia.org/wiki/Hodrick-Prescott_filter
我认为这个世界比有Dll的时候更简单。
下面是我们需要最小化的函数，以建立这个数字滤波器。
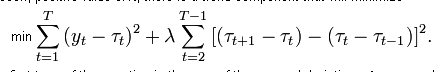
我们可以看到，在这种表述中，过滤器只能对历史数据起作用，因为为了计算当前时间的趋势线值，我们不仅需要知道这个趋势的前值，还需要知道提前一步的t[i+1]。这样的滤波器在历史上会显示出平滑曲线与kotir的精确重合（这就是作者在第一篇帖子中引用的演示），而在kotir的右边界会出现令人难以置信的过度拉伸。
下面是我在网上挖到的其他内容。
我找不到任何现成的配方来建造这个过滤器。实际上，让我们为BP的右边缘自己取并建立一个函数（上等式）。
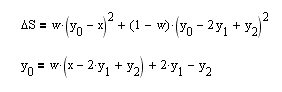
让我们通过参数y[0]-当前值对其进行导数，并将其等同于零，并立即得到所需HP-过滤器的循环表达式（下式）。让我们看看滤波器的平滑特性如何取决于平滑参数w。
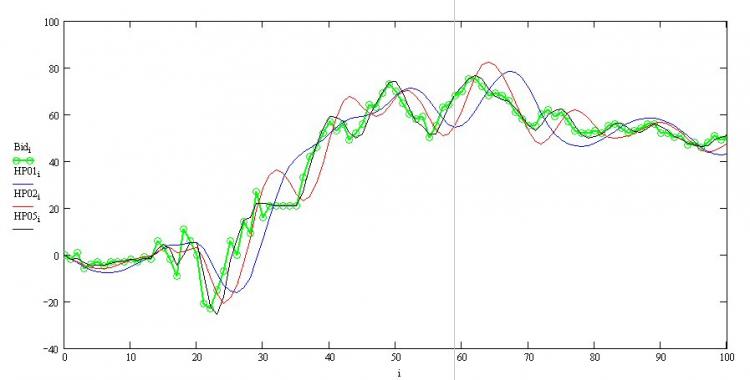
这里，绿线是cotier，黑线是w=0.5，等等。你可以看到一切工作正常--有一个不可避免的相位滞后，抗锯齿越强，相位滞后就越大，而且右边的边缘没有被重绘。现在我们也可以在MQL中进行编码。
//+------------------------------------------------------------------+
//| Moving Average HP.mq4 |
//| Code by Neutron |
//+------------------------------------------------------------------+
#property indicator_chart_window
#property indicator_color1 Blue
#property indicator_width1 3
extern double w=0.1;
int Start,i,m;
double MA[5000],Y[5000];
int start()
{
Start=5000;
MA[Start]=Open[Start];
MA[Start-1]=Open[Start-1];
for (i=Start-2;i>=0;i--) MA[i]=w*(Open[i]-2.*MA[i+1]+MA[i+2])+2.*MA[i+1]-MA[i+2];
}
int init()
{
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,MA);
return(0);
}
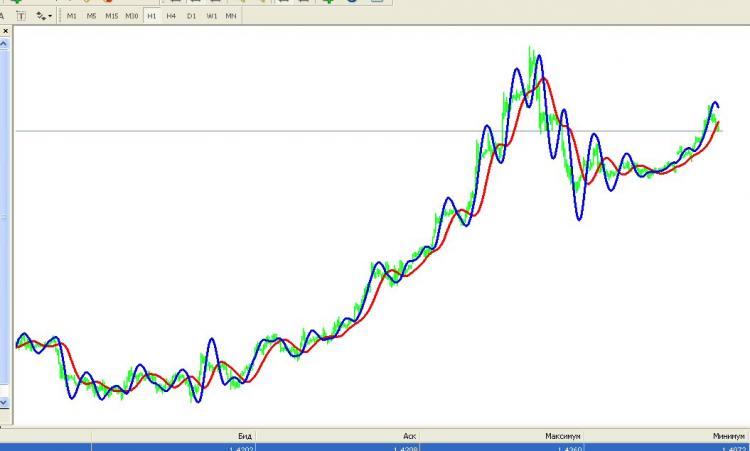
结果是这样的。
蓝色是HP，绿色是cotier，红色是二阶Watterout滤波器（用于比较）。
事实上，这个过滤器试图诚实地捕捉线性趋势。看看帖子顶部的功能--它显示，除了最小化与kotir的muving偏差（第一和），还要求最小化第二导数（第二和）!而毕竟，直线的二阶导数是零，对其最小化的要求等于对任意输入数据向量的趋势线的最大愿望的要求。我喜欢这种做法。
P.S. 有趣的是，如果在函数的表达式中要求最小化第一个导数（上面的方程）而不是第二个导数，我们会得到一个指数平均EMA的递推公式（下面的方程）。
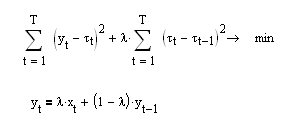
事实证明，指数平均数是所有可能的机动性中最平滑的!
红色=1600
蓝色=100
黄色 = EMA 14, cloze.
你好，亲爱的程序员们!
我想，谁会承担解决写一个指标的简单任务？ 我需要写一个指标，用Hodrick-Prescott过滤器过滤该系列。 这个函数在MATLAB中是可用的，如果我没记错的话，它可以用MATLAB编译器做成一个DLL。因此，我们需要创建一个指标，该指标将指向这个Dll。在输入端，我们应该输入以下参数 - 系列长度，平滑参数。输出是一个趋势成分（将在图表上绘制）和一个周期成分（震荡器）。
我不能自己做，我不知道MATLAB编译器和MQL4。
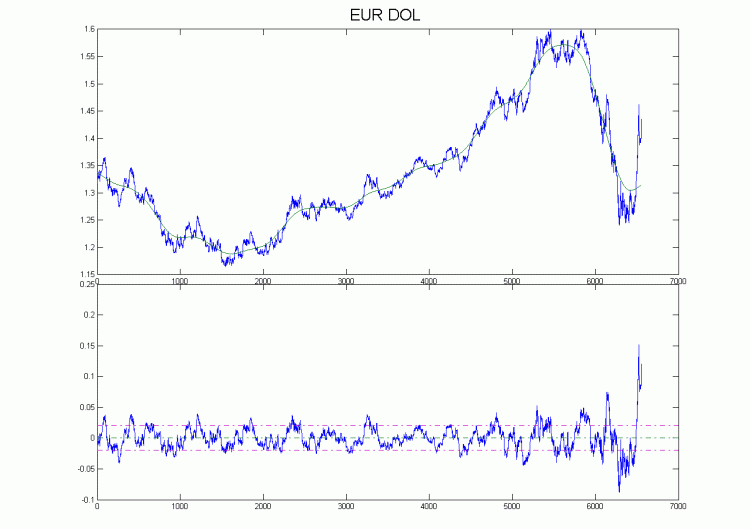
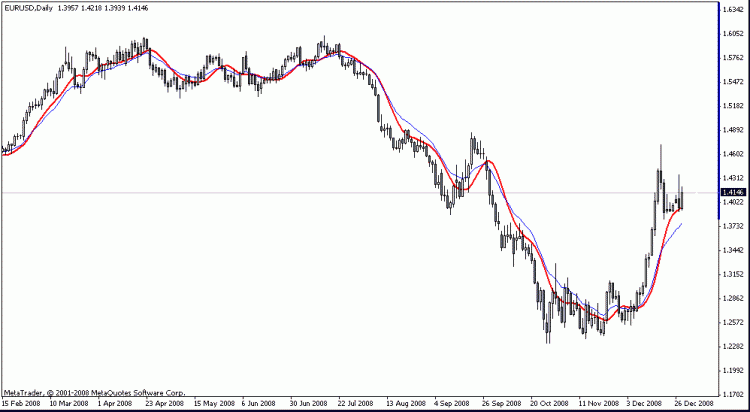
我在图表上对欧洲美元H4进行了分解。几乎在整个历史上都可以看到，价格运动的特殊性是，在突破趋势后，价格移动的距离等于前一个极值与趋势之间的差值，简而言之，振幅几乎相同。最新的数据是个例外，但那里是极端的。基本上，如果数据点的数量较少，这样的指标应该重新绘制；但是如果数据点的数量增加，例如增加到2000个，就不会出现重新绘制的问题。