주요 패턴을 설명하는 패턴 검색
상관 관계 및 회귀 이론의 모든 주요 조항은 연구 중인 데이터의 정규 분포를 가정하여 개발되었습니다. 입력 매개변수(가격)에 정규 분포가 있습니까?
이해하지 못했다
원칙적으로 RMS는 시계열(TS)을 포함하여 일련의 숫자에 포함된 모든 패턴을 시리즈에서 이러한 숫자의 모양의 특성에 관계없이 보여줍니다. 이러한 모든 미묘함과 기타 미묘함은 무작위 시리즈의 분석을 포함하여 특정 예에서 논의될 것입니다.
그러면 RMS는 실제 또는 가상의 패턴을 찾지만 정규 분포가 없기 때문에 모델의 예측 값은 0이 됩니다. 이것은 미묘함이 아니라 기초입니다.
정확히 무엇을 이해하지 못하셨습니까?
그러면 RMS는 실제 또는 가상의 패턴을 찾지만 정규 분포가 없기 때문에 모델의 예측 값은 0이 됩니다. 이것은 미묘함이 아니라 기초입니다.
RMS는 가장 적절한 종속성을 찾지 않고 가장 적절한 종속성을 찾습니다. 그리고 초기 데이터 분포의 정규성의 부재 또는 존재에 대해 별도의 토론 지점을 열고 이 재단의 감정가가 여기에서 병렬로 이야기하도록 합시다.
이해했습니다 ..... 그리고 맞습니다. 그렇습니다. 그녀, 정상! 방해만 된다
PS 모델의 예측 값은 0에 가까울 것입니다.
선형 함수부터 시작하겠습니다.
수열이 Yi = a+bxi로 주어진다고 상상해보십시오.
xi Yi
0.00000001 10.0000
1.00000001 15.0000
2.00000001 20.0000
3.00000001 25.0000
4.00000001 30.0000
5.00000001 35.0000
6.00000001 40.0000
7.00000001 45.0000
8.00000001 50.0000
9.00000001 55.0000
10.00000001 60.0000
11.00000001 65.0000
12.00000001 70.0000
13.00000001 75.0000
14.00000001 80.0000
15.00000001 85.0000
16.00000001 90.0000
17.00000001 95.0000
18.00000001 100.0000
다음은 실제 및 계산된 값의 그래프입니다. 모델 오류 2.78163E-14%: 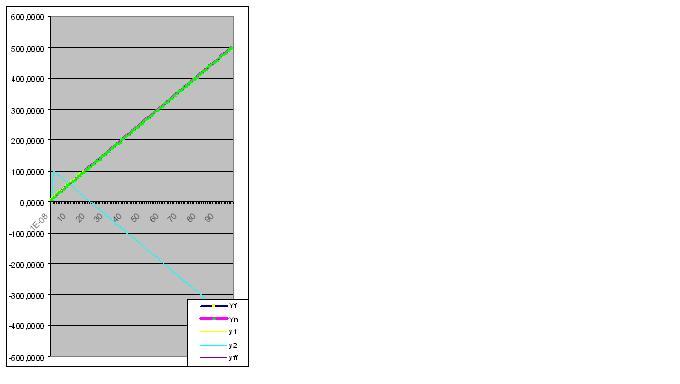
이해했습니다 ..... 그리고 맞습니다. 그렇습니다. 그녀, 정상! 방해만 된다
PS 모델의 예측 값은 0에 가까울 것입니다.
당신의 끈기 때문에 나는 Y=tg(0.1x)+2 함수를 분석하는 예를 사용하여 모델의 예측 능력을 시연하는 것으로 시작하고 처음 8자리 숫자 쌍을 입력해야 합니다.
xi Yi
0.00000001 2.0000
1.00000001 2.1003
2.00000001 2.2027
3.00000001 2.3093
4.00000001 2.4228
5.00000001 2.5463
6.00000001 2.6841
7.00000001 2.8423
오류 0.427140953%: 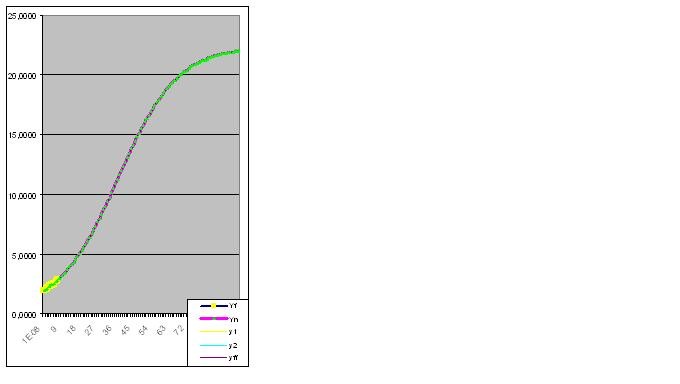
그러나 모델이 미래에 개체의 "이상한" 동작을 즉시 예측하므로 9자리 숫자 쌍을 입력할 가치가 있습니다.
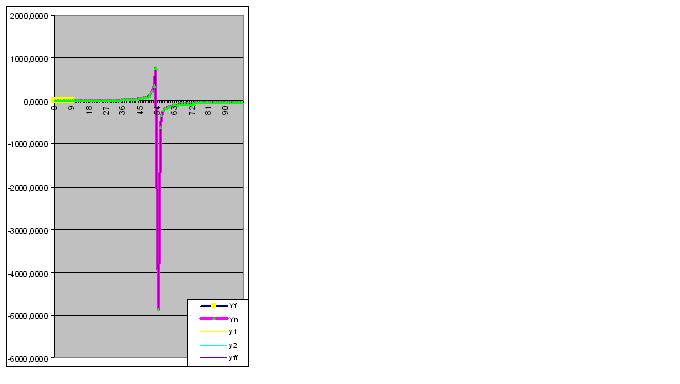
데이터를 추가로 도입하면 예측 "이상"이 원래 데이터에 더 가까워집니다.
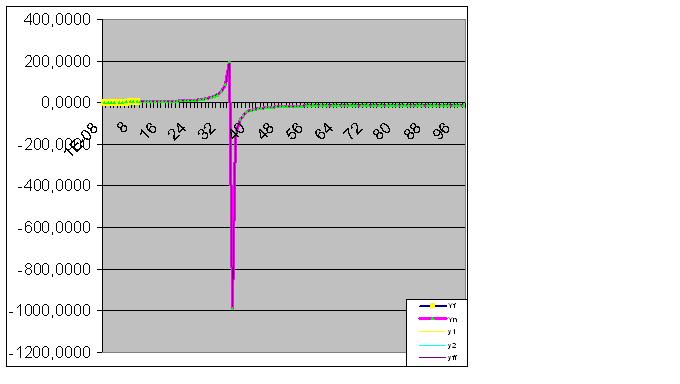
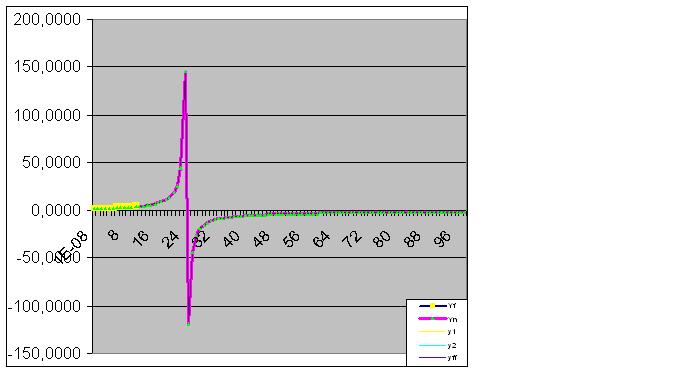
따라서 초기 데이터는 예측된 "페인트"도 수행하기 시작했습니다.
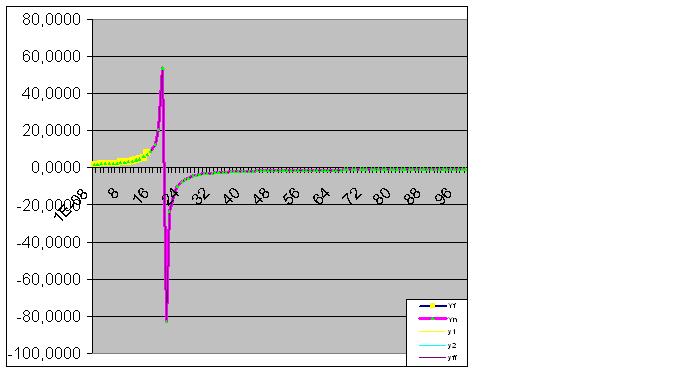
그리고 마침내 예측이 완벽하게 이루어졌습니다.
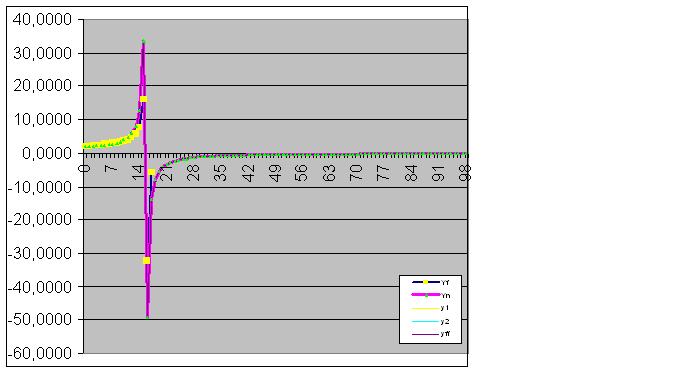
또한 모델은 이상적으로 객체의 최종 상태를 포착하므로 함수의 실제 값의 합이 컴퓨터 정확도로 RMS에 따라 계산된 값과 동일합니다.
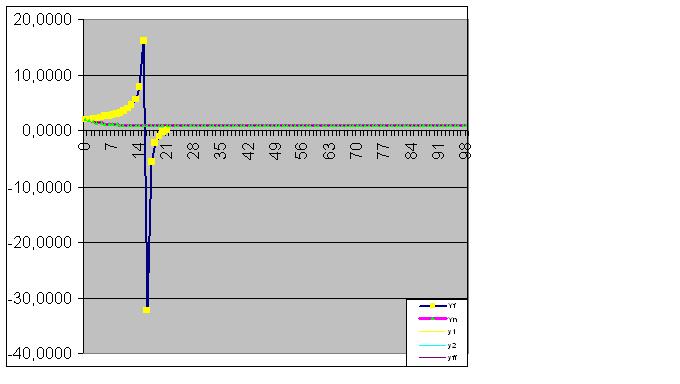
친애하는 포럼 사용자 여러분, 이것은 비밀이 아닙니다. 관련된 것은 시장의 주요 패턴을 설명하는 종속성을 찾는 문제입니다. 여기에서 우리는 이 문제에 대한 참가자의 다양한 제안과 다양한 출처에서 여기까지 축적된 이론적이고 실용적인 자료를 포함하여 가능한 모든 분석 수단을 통해 이 문제의 해결책에 접근하려고 노력할 것입니다. 이 작업의 결과로 이 기능의 형태만 놓고 본다면 그 시간과 노력이 헛되지 않았다는 생각이 듭니다.
선형 의존성, 포물선, 쌍곡선, 지수, 사인, 코사인, 탄젠트, 코탄젠트 등의 잘 알려진 패턴과 그 조합을 설명하는 간단한 예를 사용하여 RMS의 기능을 설명하는 것으로 시작하겠습니다. 시장. 필요한 경우 건설적인 제안과 건전한 비판으로 이러한 충동에 동참해 주시기 바랍니다.