연기
나는 그의 책에서와 같이 R. Vince에 따라 최적의 f를 계산하기 위해 다음 함수를 만들었습니다.
//---------переменные для расчета лота по оптимальному f Ральфа Винса int Mas_Outcome_of_transactions [ 10000 ]; // Массив профитов/убытков закрытых позиций extern double D = - 628 ; // максимальный убыток по сделке //+------------------------------------------------------------------+ //| expert deinitialization function | //+------------------------------------------------------------------+ int deinit() { //---- if (Monitor==true) { for ( int a= 0 ;a<= 3 ;a++) { string N= DoubleToStr (a, 0 ); ObjectDelete (N); } } //---- //--- Расчет оптимального f --- int Qnt= 0 ; // Счётчик количества ордеров ArrayInitialize (Mas_Outcome_of_transactions, 0 ); // Обнуление массива double f= 0.01 , SUMM, MUL, HPR, TWR_Rez= 0 , TWR= 1.0 , G; int orderIndex; for (orderIndex = 0 ; orderIndex< OrdersHistoryTotal (); orderIndex++) { if (! OrderSelect (orderIndex, SELECT_BY_POS, MODE_HISTORY)) { Print ( "Ошибка при доступе к исторической базе (" , GetLastError (), ")" ); continue ; } if (( OrderSymbol () != Symbol ()) || ( OrderMagicNumber () != magic) || ( OrderCloseTime ()== 0 )) { continue ; } Qnt++; // увеличиваем счетчик закрытых ордеров int lastType = OrderType (); double lastLots = OrderLots (); double lastProfit = OrderProfit () + OrderSwap (); Mas_Outcome_of_transactions[Qnt] = lastProfit; // Заполняем массив профитом/лоссом по всем закрытым позициям SUMM=SUMM+lastProfit; //TWR = TWR*(1+f*(-lastProfit/(D))); } // Print("Закрытых позиций = ", Qnt, " Профит/лосс = ", SUMM); for (f = 0.01 ; f<= 1.0 ; f=f+ 0.01 ) //цикл перебора переменной f для поиска оптимального ее значения,при котором TWR-максимально { for ( orderIndex = 1 ;orderIndex<Qnt; orderIndex++) //при заданной f проходим по всем закрытым ордерам { // и считаем относительный конечный капитал (TWR) TWR = TWR*( 1 +f*(-Mas_Outcome_of_transactions[orderIndex]/(D))); // TWR - это произведение всех HPR //if (TWR>TWR_Rez) {TWR_Rez = TWR; Print(" TWR = ",TWR_Rez, " при f = ", f);} // else break; } if (TWR>TWR_Rez) { TWR_Rez = TWR; G= MathPow (TWR_Rez, 0.001988 ); // 1/503 сделки по данной торговой системе, как в книжке: в степени 1/N Print ( " TWR = " ,TWR_Rez, " G = " ,G, " при f = " , f);} // если текущий TWR > результирующего, else break ; // то результирующий делаем равным текущему, иначе переходим на след итерацию цикла по f } Print ( "Закрытых позиций = " , Qnt, " Нетто Профит/лосс = " , SUMM, " У последней " ,Qnt, " закрытой позы профит/лосс = " , Mas_Outcome_of_transactions[Qnt]); return ( 0 ); }
어드바이저를 테스트한 후, 위에서 두 번째 줄, 즉 TWR=1.#INF인 로그에서 이것이 무엇을 의미하는지 알려주십시오.
그것은 무엇입니까? - 범위 2배를 벗어났습니까?
그렇다면 최적의 f를 계산하는 방법은 무엇입니까?
나는 그의 책에서와 같이 R. Vince에 따라 최적의 f를 계산하기 위해 다음 함수를 만들었습니다.
어드바이저를 테스트한 후, 위에서 두 번째 줄, 즉 TWR=1.#INF인 로그에서 이것이 무엇을 의미하는지 알려주십시오.
그것은 무엇입니까? - 범위 2배를 벗어났습니까?
그렇다면 최적의 f를 계산하는 방법은 무엇입니까?
| 3289 | 로시 26.10.2005 20:49 그리고 "1.INF", "1.IND"라는 숫자는 모듈러스가 너무 큰 값이나 0/0과 같은 정의되지 않은 값(내 생각에는 그렇게 생각합니다)을 의미합니다. |
| 4464 | 슬라바 27.10.2005 09:59 그리고 "1.INF", "1.IND"라는 숫자는 모듈러스가 너무 큰 값이나 0/0과 같은 정의되지 않은 값(내 생각에는 그렇게 생각합니다)을 의미합니다. 그렇습니다. 이들은 부동 주문 오버플로(1.INF) 및 이중 주문 오버플로(1.IND)입니다. 나누기 전에 제수를 0으로 확인 |
Anton Trefolev http://forum.alpari.ru/member.php?u=56027 은 최적의 f에 대해 작업했으며 그에게 요청할 수 있습니다. (내가 기억하는 한) 3개월 만에 11,000%를 모금한 유명한 사람. 그런 다음 그는 야간 십자가에서 퍼짐을 넓혀 산소를 차단했습니다. 그럼에도 불구하고 계정을 100,000 이상으로 분산하는 것이 가능했으며 그 후에는 팸을 닫아야했습니다.
| 3289 | 로시 26.10.2005 20:49 그리고 "1.INF", "1.IND"라는 숫자는 모듈러스가 너무 큰 값이나 0/0과 같은 정의되지 않은 값(내 생각에는 그렇게 생각합니다)을 의미합니다. |
| 4464 | 슬라바 27.10.2005 09:59 그리고 "1.INF", "1.IND"라는 숫자는 모듈러스가 너무 큰 값이나 0/0과 같은 정의되지 않은 값(내 생각에는 그렇게 생각합니다)을 의미합니다. 그렇습니다. 이들은 부동 주문 오버플로(1.INF) 및 이중 주문 오버플로(1.IND)입니다. 나누기 전에 제수를 0으로 확인 |
문제의 사실은 나눗셈, 연속 곱셈이 없다는 것입니다(그의 R. Vince 공식에 따르면 그게 전부입니다).
저것들. mql은 이 문제(TWR의 올바른 계산)를 해결할 수 없음을 의미합니까?
저것들. ddl, matkad 등을 통해 해결하시겠습니까?
| 3289 | 로시 26.10.2005 20:49 그리고 "1.INF", "1.IND"라는 숫자는 모듈러스가 너무 큰 값이나 0/0과 같은 정의되지 않은 값(내 생각에는 그렇게 생각합니다)을 의미합니다. |
| 4464 | 슬라바 27.10.2005 09:59 그리고 "1.INF", "1.IND"라는 숫자는 모듈러스가 너무 큰 값이나 0/0과 같은 정의되지 않은 값(내 생각에는 그렇게 생각합니다)을 의미합니다. 그렇습니다. 이들은 부동 주문 오버플로(1.INF) 및 이중 주문 오버플로(1.IND)입니다. 나누기 전에 제수를 0으로 확인 |
float 주문(1.INF)이 오버플로되면 어떻게 됩니까?
f에 대한 루프의 후속 반복은 현재 결과를 반환합니까? 또는 더 사이클 카운트? TWR의 수치에는 관심이 없고, TWR의 누적 합계와 곱하여 구한 f의 값에 관심이 있습니다.
이 코드에서:
for (f = 0.01 ; f<= 1.0 ; f=f+ 0.01 ) //цикл перебора переменной f для поиска оптимального ее значения,при котором TWR-максимально { for ( orderIndex = 1 ;orderIndex<Qnt; orderIndex++) //при заданной f проходим по всем закрытым ордерам { // и считаем относительный конечный капитал (TWR) TWR = TWR*( 1 +f*(-Mas_Outcome_of_transactions[orderIndex]/(D))); // TWR - это произведение всех HPR } if (TWR>TWR_Rez) { TWR_Rez = TWR; G= MathPow (TWR_Rez, 0.001988 ); // 1/503 сделки по данной торговой системе, как в книжке: в степени 1/N Print ( " TWR = " ,TWR_Rez, " G = " ,G, " при f = " , f);} // если текущий TWR > результирующего, else break ; // то результирующий делаем равным текущему, иначе переходим на след итерацию цикла по f }
문제의 사실은 나눗셈, 연속 곱셈이 없다는 것입니다(그의 R. Vince 공식에 따르면 그게 전부입니다).
저것들. mql을 통해 이 질문(TWR의 올바른 계산)을 해결할 수 없습니까?
저것들. ddl, matkad 등을 통해 해결하시겠습니까?
곱할 때 오버플로도 발생할 수 있습니다.
나도 알아 그런 다음 기하 평균 방법으로 최적 f를 계산하는 방법은 무엇입니까? 나는 모든 공식을 작성했으며 모든 것이 코드에서 정확합니다.
아마도 최적에 대해 생각해야 할 것입니다. 계산 옵션을 찾을 수 있습니다.
그리고 TWR을 이전 값(TWR_Rez)과 비교하지 않고 기하학적 평균 G와 일부 G_Rez를 비교한다면? 결국 number_1의 차수 K의 루트가 number_2의 동일한 차수 K의 루트보다 크면 number_1은 number_2보다 큽니다 ! :))))))))
그리고 이미 루트(변수 G)를 계산하면 제품이 실제로 요소로 분할되고(왜 부품으로 귀찮게) 각 요소에서 루트를 가져오는 경우 오버플로가 없습니다. 결국, 곱의 근은 그 요인의 근의 곱과 같습니다 ! :)))
계산 시간이 크게 증가하지만 오버플로 및 소란은 없습니다. 또한 계산의 정확도가 크게 향상됩니다.
그리고 TWR 변수를 표시하기로 결정했다면 int 유형의 추가 변수에 해당 비트를 저장하고 Print에서 TWR 비트를 인쇄해야 합니다(예: "89605994539435e+1234121"). 그러나 당신은 그것을 필요로합니까?
나도 알아 그런 다음 기하 평균 방법으로 최적 f를 계산하는 방법은 무엇입니까? 나는 모든 공식을 작성했으며 모든 것이 코드에서 정확합니다.
연기
로마 14.08.2011 06:37
얘들 아, 이제 R. Vince에 따르면 기하 평균 방법을 사용하여 최적의 f(로트의 부피를 계산하기 위한)를 찾고 있습니다.
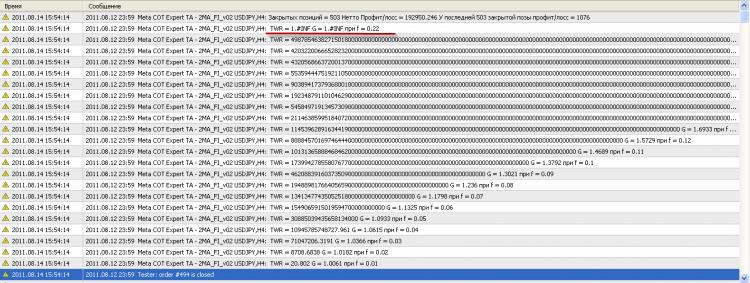
작업: 주문 내역을 살펴보고 0.01에서 1로 f = 0.01 단계로 코드로 이동하면서 TWR이 최대인 최적 값을 찾아야 합니다.
두 개의 낮은 공식과 거래에서 가장 큰 손실의 값은 D=-458 로 알려져 있습니다.
특히 최적의 f를 찾기 위한 반복 주기와 코드에서 추가로 구성할 위치.
다음은 int deinit()의 시작 코드입니다. 정기적으로 이익에 대해 전략 테스터에 인쇄합니다.
//+------------------------------------------------------------------+ //| expert deinitialization function | //+------------------------------------------------------------------+ int deinit() { //--- Расчет оптимального f --- double SUMM, MUL, HPR, TWR, G; double D=-458; int orderIndex; for (orderIndex = ( OrdersHistoryTotal () - 1 ); orderIndex >= 0 ; orderIndex--) { if (! OrderSelect (orderIndex, SELECT_BY_POS, MODE_HISTORY)) { Print ( "Ошибка при доступе к исторической базе (" , GetLastError (), ")" ); continue ; } if (( OrderSymbol () != Symbol ()) || ( OrderMagicNumber () != magic) || ( OrderCloseTime ()== 0 )) { continue ; } int lastType = OrderType (); double lastLots = OrderLots (); double lastProfit = OrderProfit () + OrderSwap (); SUMM=SUMM+lastProfit; } Print ( "Профит = " , SUMM); return ( 0 ); }