Discussion de l'article "Réseaux de neurones de troisième génération : Réseaux profonds" - page 2

Nouveau commentaire
 
vlad1949:

Ce n'est pas une question pour moi. C'est tout ce que vous avez à dire sur l'article ?

Qu'est-ce qu'il y a à dire sur l'article ? C'est une réécriture typique. C'est la même chose dans d'autres sources, mais avec des mots légèrement différents. Même les images sont les mêmes. Je n'ai rien vu de nouveau, c'est-à-dire d'auteur.

Je voulais essayer les exemples, mais c'est dommage. La section est pour MQL5, mais les exemples sont pour MQL4.

 

vlad1949

Cher Vlad !

J'ai regardé dans les archives, vous avez une documentation R assez ancienne. Il serait bon de passer aux copies ci-jointes.

Dossiers :
Doc_R.zip  2181 kb
 

vlad1949

Cher Vlad !

Pourquoi n'avez-vous pas réussi à faire fonctionner le testeur ?

J'ai tout fonctionne sans problème. Mais le schéma est sans indicateur : l'Expert Advisor communique directement avec R.

 

Jeffrey Hinton, inventeur des réseaux profonds : "Les réseaux profonds ne sont applicables qu'aux données dont le rapport signal/bruit est élevé. Les séries financières sont tellement bruyantes que les réseaux profonds ne sont pas applicables. Nous avons essayé, mais sans succès."

Écoutez ses conférences sur YouTube.

 
gpwr:

Jeffrey Hinton, inventeur des réseaux profonds : "Les réseaux profonds ne sont applicables qu'aux données dont le rapport signal/bruit est élevé. Les séries financières sont tellement bruyantes que les réseaux profonds ne sont pas applicables. Nous avons essayé, mais sans succès."

Écoutez ses conférences sur YouTube.

Compte tenu de votre message dans le fil de discussion parallèle.

Le bruit est compris différemment dans les tâches de classification et dans l'ingénierie radio. Un prédicteur est considéré comme bruyant s'il est faiblement lié (a un faible pouvoir prédictif) à la variable cible. Une signification complètement différente. Il faut rechercher des prédicteurs qui ont un pouvoir prédictif pour différentes classes de la variable cible.

 
J'ai une compréhension similaire du bruit. Les séries financières dépendent d'un grand nombre de prédicteurs, dont la plupart nous sont inconnus et qui introduisent ce "bruit" dans les séries. En utilisant uniquement des variables prédictives accessibles au public, nous sommes incapables de prédire la variable cible, quels que soient les réseaux ou les méthodes que nous utilisons.
 
gpwr:
J'ai une compréhension similaire du bruit. Les séries financières dépendent d'un grand nombre de prédicteurs, dont la plupart nous sont inconnus et qui introduisent ce "bruit" dans les séries. En utilisant uniquement les prédicteurs accessibles au public, nous sommes incapables de prédire la variable cible, quels que soient les réseaux ou les méthodes que nous utilisons.
Voir mon fil de discussion.
 
faa1947:

vlad1949

Cher Vlad !

Pourquoi n'avez-vous pas réussi à faire fonctionner le testeur ?

J'ai tout fonctionne sans problème. Vrai le schéma sans indicateur : le conseiller communique directement avec R.

llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll

Bonjour SanSanych.

L'idée principale est donc de faire de la multidevise avec plusieurs indicateurs.

Sinon, bien sûr, vous pouvez tout mettre dans un Expert Advisor.

Mais si la formation, les tests et l'optimisation doivent être mis en œuvre à la volée, sans interrompre le trading, alors la variante avec un Expert Advisor sera un peu plus difficile à mettre en œuvre.

Bonne chance !

PS. Quel est le résultat des tests ?

 

Bonjour SanSanych.

Voici quelques exemples de détermination du nombre optimal de clusters que j'ai trouvés sur un forum anglophone. Je n'ai pas pu tous les utiliser avec mes données. Le paquet 11 "clusterSim" est très intéressant.

--------------------------------------------------------------------------------------

#
n = 100
g = 6 
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))), 
                y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
plot(d)
--------------------------------------
#1 
library(fpc)
pamk.best <- pamk(d)
cat("number of clusters estimated by optimum average silhouette width:", strpamk.best$nc, "\n")
plot(pam(d, pamk.best$nc))

#2 we could also do:
library(fpc)
asw <- numeric(20)
for (k in 2:20)
  asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
cat("silhouette-optimal number of clusters:", k.best, "\n")
---------------------------------------------------
#3. Calinsky criterion: Another approach to diagnosing how many clusters suit the data. In this case 
# we try 1 to 10 groups.
require(vegan)
fit <- cascadeKM(scale(d, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
# 5 clusters!
-------------------
4. Determine the optimal model and number of clusters according to the Bayesian Information 
Criterion for expectation-maximization, initialized by hierarchical clustering for parameterized 
Gaussian mixture models
library(mclust)
# Run the function to see how many clusters
# it finds to be optimal, set it to search for
# at least 1 model and up 20.
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
cat("model-based optimal number of clusters:", m.best, "\n")
# 4 clusters
plot(d_clust)
----------------------------------------------------------------
5. Affinity propagation (AP) clustering, see http://dx.doi.org/10.1126/science.1136800 
library(apcluster)
d.apclus <- apcluster(negDistMat(r=2), d)
cat("affinity propogation optimal number of clusters:", length(d.apclus@clusters), "\n")
# 4
heatmap(d.apclus)
plot(d.apclus, d)
---------------------------------------------------------------------
6. Gap Statistic for Estimating the Number of Clusters. 
See also some code for a nice graphical 
output . Trying 2-10 clusters here:
library(cluster)
clusGap(d, kmeans, 10, B = 100, verbose = interactive())
-----------------------------------------------------------------------
7. You may also find it useful to explore your data with clustergrams to visualize cluster 
assignment, see http://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/&nbsp; 
for more details.
-------------------------------------------------------------------
#8. The NbClust package  provides 30 indices to determine the number of clusters in a dataset.
library(NbClust)
nb <- NbClust(d, diss = NULL, distance = "euclidean", 
        min.nc=2, max.nc=15, method = "kmeans", 
        index = "alllong", alphaBeale = 0.1)
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))
# Looks like 3 is the most frequently determined number of clusters
# and curiously, four clusters is not in the output at all!
-----------------------------------------
Here are a few examples:
d_dist <- dist(as.matrix(d))   # find distance matrix 
plot(hclust(d_dist))           # apply hirarchical clustering and plot
----------------------------------------------------
#9 Bayesian clustering method, good for high-dimension data, more details:
# http://vahid.probstat.ca/paper/2012-bclust.pdf
install.packages("bclust")
library(bclust)
x <- as.matrix(d)
d.bclus <- bclust(x, transformed.par = c(0, -50, log(16), 0, 0, 0))
viplot(imp(d.bclus)$var); 
plot(d.bclus); 
ditplot(d.bclus)
dptplot(d.bclus, scale = 20, horizbar.plot = TRUE,varimp = imp(d.bclus)$var, horizbar.distance = 0, dendrogram.lwd = 2)
-------------------------------------------------------------------------
#10 Also for high-dimension data is the pvclust library which calculates 
#p-values for hierarchical clustering via multiscale bootstrap resampling. Here's #the example from the documentation (wont work on such low dimensional data as in #my example):
library(pvclust)
library(MASS)
data(Boston)
boston.pv <- pvclust(Boston)
plot(boston.pv)
------------------------------------
###Automatically cut the dendrogram
require(dynamicTreeCut)
ct_issues <- cutreeHybrid(hc_issues, inverse_cc_combined, minClusterSize=5)
-----
FANNY <- fanny(as.dist(inverse_cc_combined),, k = 3, maxit = 2000) 
FANNY$membership MDS <- smacofSym(distMat)$conf 
plot(MDS, type = "n") text(MDS, label = rownames(MDS), col = rgb((FANNY$membership)^(1/1)))
-----
m7 <- stepFlexmix
----------------------
#11 "clusterSim" -Department of Econometrics and Computer Science, University of #Economics, Wroclaw, Poland
http://keii.ue.wroc.pl/clusterSim
See file ../doc/clusterSim_details.pdf for further details
data.Normalization Types of variable (column) and object (row) normalization formulas
Description
Types of variable (column) and object (row) normalization formulas
Usage
data.Normalization (x,type="n0",normalization="column")
Arguments
x vector, matrix or dataset
type type of normalization: n0 - without normalization
n1 - standardization ((x-mean)/sd)
n2 - positional standardization ((x-median)/mad)
n3 - unitization ((x-mean)/range)
n3a - positional unitization ((x-median)/range)
n4 - unitization with zero minimum ((x-min)/range)
n5 - normalization in range <-1,1> ((x-mean)/max(abs(x-mean)))
n5a - positional normalization in range <-1,1> ((x-median)/max(abs(x-median)))
n6 - quotient transformation (x/sd)
n6a - positional quotient transformation (x/mad)
n7 - quotient transformation (x/range)
n8 - quotient transformation (x/max)
n9 - quotient transformation (x/mean)
n9a - positional quotient transformation (x/median)
n10 - quotient transformation (x/sum)
n11 - quotient transformation (x/sqrt(SSQ))
normalization "column" - normalization by variable, "row" - normalization by objec
See file ../doc/HINoVMod_details.pdf for further details


Dans le prochain post les calculs avec mes données

 

Le nombre optimal de clusters peut être déterminé par plusieurs packages et en utilisant plus de 30 critères d'optimalité. D'après mes observations, le critère le plus utilisé est lecritère de Calinsky.

Prenons les données brutes de notre ensemble à partir de l'indicateur dt . Il contient 17 prédicteurs, la cible y et le corps de chandelier z.

Les dernières versions des paquets "magrittr" et "dplyr" contiennent de nombreuses nouvelles fonctionnalités, dont l'une est le "pipe" - %>%. Elle est très pratique lorsque vous n'avez pas besoin de sauvegarder les résultats intermédiaires. Préparons les données initiales pour le clustering. Prenons la matrice initiale dt, sélectionnons-en les 1000 dernières lignes, puis sélectionnons-y les 17 colonnes de nos variables. Nous obtenons une notation plus claire, rien de plus.

> library(magrittr)
> x<-dt %>% tail( .,1000)%>% extract( ,1:17)

1.

> library(fpc)
> pamk.best <- pamk(x)
> cat("number of clusters estimated by optimum average silhouette width:", pamk.best$nc, "\n")
> number of clusters estimated by optimum average silhouette width: h: 2

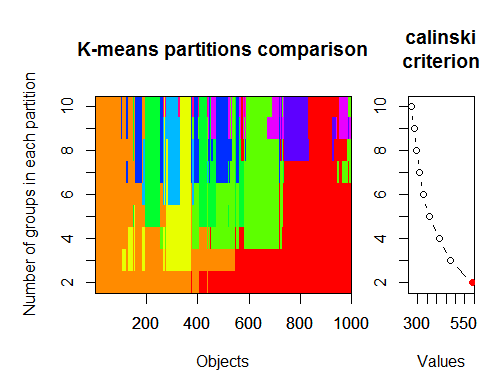
2. Critère de Calinsky : une autre approche pour diagnostiquer le nombre de grappes qui conviennent aux données. Dans ce cas

nous essayons de 1 à 10 groupes.

> require(vegan)
> fit <- cascadeKM(scale(x, center = TRUE,  scale = TRUE), 1, 10, iter = 1000)
> plot(fit, sortg = TRUE, grpmts.plot = TRUE)

> calinski.best <- as.numeric(which.max(fit$results[2,]))
> cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
Calinski criterion optimal number of clusters: 2
3) Déterminer le modèle optimal et le nombre de grappes selon le critère d'information bayésien pour la maximisation de l'espérance, initialisé par le regroupement hiérarchique pour les modèles de mélange gaussien paramétrés.

Modèles de mélange gaussien 

> library(mclust)
#  Run the function to see how many clusters
#  it finds to be optimal, set it to search for
#  at least 1 model and up 20.
> d_clust <- Mclust(as.matrix(x), G=1:20)
> m.best <- dim(d_clust$z)[2]
> cat("model-based optimal number of clusters:", m.best, "\n")
model-based optimal number of clusters: 7
123456789...17
Nouveau commentaire