Renter - page 6

New comment
 
Neutron:

No, no. Not wrong. Here is the dependence of the withdrawal amount, which follows from the iterative formula (in red), and from the analytical dependence (in blue).

You can see that they coincide and there is a maximum in k (on the previous page of the topic).



Clearly, you don't have discrete withdrawals, but necessarily continuous withdrawals in equal shares. So there is no solution to withdraw differently in different periods. So there is no solution to withdrawing everything at the end without withdrawing before. This does not follow from the conditions of the problem, but from the formulas you apply (k is fixed, not variable ki, i=0...T)
 
That's right.
 

Total funds withdrawn

the effect becomes tangible if the growth rate is high enough

 

I have similar dependencies.

Now I'm trying to decompose the expression for the derivative into powers of k, but it's no good - I have to hold six orders of magnitude. It is clear that this cannot be solved analytically. Maybe there are other ideas? Someone mentioned diphurcs...

 
we need to figure it out.
 
Neutron:

I have similar dependencies.

Now I'm trying to decompose the expression for the derivative into powers of k, but it's no good - I have to hold six orders of magnitude. It is clear that this cannot be solved analytically. Maybe there are other ideas? Someone mentioned diphurcs...


It's a bit complicated analytically. On q and t. It depends somehow in a tricky way :) As q increases, as t increases, the fraction of optimum removal consistently decreases
 
Neutron:

I have similar dependencies.

Now I'm trying to decompose the expression for the derivative into powers of k, but it's no good - I have to hold six orders of magnitude. It is clear that this cannot be solved analytically. Maybe there are other ideas? Someone mentioned diphurcs...

Diffurcation will not work so easily - a simple rewriting of the difference in the derivative is wrong and will distort the result, while the exact transformation will still lead to an equation that will make one's hair stand on end even higher. IMHO, don't bother, in this case it is easier to solve the problem numerically since the function is smooth and has one extremum, you can eat your fill for such fast optimization algorithms...
 

You can go from the particular to the general. For example, if t = 1, you can withdraw money only once, and hence you have to withdraw it in the amount of q. Then consider the case for t = 2, t = 3, etc.

I.e. if at t = 2 it is optimal to withdraw less than q at a time, then find an extremum and generalize for all q at t = 2.

Similarly for t = 3, t = 4 etc.

From the value of the extremum, it will be possible to obtain the size of the withdrawal as f(t)

 

A connected vessel scheme can be considered to make up the DU.

Initial volume of the first vessel B0

 
Reshetov:

You can go from the particular to the general. For example, if t = 1, you can withdraw money only once, and hence you have to withdraw in the amount of q. Then consider the case for t = 2, t = 3, etc.

From the value of the extremum we will be able to get the size of the withdrawal as f(t)


You may be right. Except that for t = 3 we already have according to the equation degree k - three in the first derivative df(k)/dk=0, and we need to look for roots of the cubic equation with all that it implies... That is, we can't get any further than t=3 in this scenario. Recall that 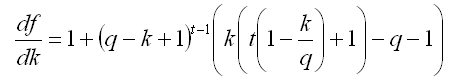, and for t=1 optimum size k=q, for t=2 k=q, for t=3 k=q. But further increasing t and solving analytically doesn't work. If you solve it numerically, you can see that at deposit growth rate q is within 10% per month, the optimal withdrawal rate becomes lower than q at t>30 months.

The conclusion follows: if the TS reliability is such that the average lifetime of the deposit does not exceed 3 years, then the optimal behavior is a monthly withdrawal of all gained profit (the deposit is not growing). Otherwise we need to find an analytical solution for the optimal withdrawal percentage k and act according to the formula. This scenario guarantees maximum pocket money for the expected life time of the deposit.


In order to make DU we may consider the scheme of connected vessels.Initial volume of the first vessel B0

If vessels (fluid flow) are in dynamic equilibrium (i.e. how much fluid per unit time flows into the first vessel as much flows out of the last one) the problem about the water level in each vessel is solved elementary and is not reduced to the deposit problem. If to consider vessels in process of their filling it is not clear the analogy with the deposit. avtomat ,explain, please, what you meant proposing such interpretation?

P.S. The appeal to get an approximate analytical solution of the equation df/dk=0 is still valid. Any ideas are welcome.

12345678910111213...31
New comment
Reason: