Discussion of article "Combinatorics and probability theory for trading (Part II): Universal fractal"
If it is possible, I ask the author of this article to consider the following arguments:
So far I see that the principle of the golden ratio can be used to construct fractal-probabilistic chains forming a complete group of events, but I honestly do not see what such an approach can give. It seems that the golden ratio is also connected with fibo series, but again I don't see how it can be applied and for what, if you have ideas you can write here, I think it will be a plus here. And so in general these processes have already formed in my head, in general that is all that is needed to derive more complex formulas. So far the obtained fractals fulfil their task. There everything goes from complex to simple and so on. I can think about the application of the golden ratio, but I can't see how it will be useful. Fibo series too, everyone says fibo-fibo ... Ololo, they hear a clever word and repeat it like a parrot. I always proceed from the fact that a mathematical principle corresponds to a particular problem, and always find a solution to any problem after some time. The tool of the solution is selected in the process, the brain itself finds it, and if possible finds similarities with something that is on the ear. In other words, first we determine what we need to find and then we look for ways to solve the problem. I would be more interested to hear specific problems, and you can make a separate article with such solutions, it would be interesting and fun I think. Within the framework of these problems we can apply the golden ratio and anything else, as long as the result is really necessary and gives a concrete benefit to someone. So you can write suggestions.
If it is possible, I ask the author of this article to consider the following arguments:
This is just a hackneyed myth of alleged fibo and ZS everywhere....
The funny thing is that if you take any pot and twist it well you can find in it both fibo and golden ratio and pi and e and many other things....
It's just a hackneyed myth of supposedly fibo and ZS everywhere and anywhere...
The funny thing is that if you take any pot and twist it well you can find in it the fibo and the golden ratio and the number of pi and the number of e and many other things....
Fiba (they are also the golden ratio, which many people do not realise) are searched for, i.e. seen, extremely easily. Because they are exponentials. Which in their turn are sums...In general, you can talk about elementary things from school (!!!) for a long time, but it's useless.
You can also do it like this:
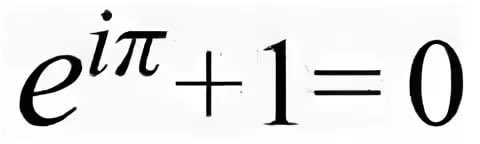
beautiful, mysterious...the connection of FIBO with Fourier...the world constants in one glass...and other stuff.
It's just a hackneyed myth of supposedly fibo and ZS everywhere and anywhere...
The funny thing is that if you take any pot and spin it well, you can find in it the fibo and the golden ratio and the number of pi and the number of e and many other things....
you can also find head and shoulders in the pot if you put it on your head.)
It's just a hackneyed myth that Fibo and ZS are everywhere and everywhere....
The funny thing is that if you take any pot and twist it well you can find in it fibo and golden ratio and pi and e and many other things....
I couldn't agree more )) it's really true. Traders are very fond of looking for a hidden meaning where there is none at all ). I am trying to convey the same thing carefully to people, but I don't know how to do it without telling the truth, and the truth is cruel ). I have come to the point that there is a problem and there is a set of possible solutions, and anything other than that is a waste of time. In order to get a solution, you must first clearly set the problem and have at least a superficial idea of the possible ways of its solution, if there are no such ways, then begins what was above, Fibonacci, Euler's formulae and other very beautiful but so much useless rubbish that you involuntarily begin to read between the lines. Each tool has its own task. In this connection, I propose to get down to specifics (specific tasks).
So far I see that the golden ratio principle can be used to construct fractal probability chains that form a complete group of events, but I honestly don't see what this approach can do. It seems that the golden ratio is also connected with the fibo series, but again I don't see how it can be applied and for what, if you have ideas you can write here, I think it will be a plus here. And so in general these processes have already formed in my head, in general that is all that is needed to derive more complex formulas. So far the obtained fractals fulfil their task. There everything goes from complex to simple and so on. I can think about the application of the golden ratio, but I can't see how it will be useful. Fibo series too, everyone says fibo-fibo ... Ololo, they hear a clever word and repeat it like a parrot. I always proceed from the fact that a mathematical principle corresponds to a particular problem, and always find a solution to any problem after some time. The tool of the solution is selected in the process, the brain itself finds it, and if possible finds similarities with something that is on the ear. In other words, first we determine what we need to find and then we look for ways to solve the problem. I would be more interested to hear specific problems, and you can make a separate article with such solutions, it would be interesting and fun I think. Within the framework of these problems we can apply the golden ratio and anything else, as long as the result is really necessary and gives a concrete benefit to someone. So you can write suggestions.
1. Maybe everyone has heard about this "ololo", but I did not write about fibo, because I do not advise to "pull" fibo levels, although if they are calculated correctly, they can be used, but in combination with Elliott waves.
Of course, this is not all there is, you realise how time-consuming and painstaking this work is, but I started this thread for a reason. I will try to do everything that depends on me, and in general such questions, to be honest, should be dealt with by a whole team of mathematicians and programmers, if not a whole institute. What can one person do against it? Even if you have a super brain, there is so much data to process that you can go crazy. I am trying to set those tasks that are commensurate with my time and capabilities, yes I can do more, but it does not depend on me now. Time is the most valuable resource. If there were people who are interested in complex analyses and complete dedication I would be happy to do it. Nevertheless, the branch will continue and I will cover the material that I can, I always try to tell something new, as far as I can.
The myth about the universality of the golden ratio in nature has grown so much that people don't even bother themselves with real checks, succumbing to the charms of the beauty of the very idea of the ratio of the whole and its parts, but in fact it is not so:
- shells of mollusks-nautilus (which are usually illustrated in articles about magic of WD) contrary to popular opinion do not correspond to WD.
- proportions of a human body from the famous Leonardo Da Vinci's drawing "Vitruvian Man" are not observed in relation to real people.
- Parthenon, Pyramids, other objects very inaccurately correspond to RS (drawn by mysticism lovers).
- objective psychological researches with the purpose to reveal whether the EQ is the basis of perception of beauty have successfully failed.
- Finally, quantitative tests of breakdown/rejection of levels in trading do not show that EQ is something particularly important either.
The only reason why markets can sometimes (key word ANOTHER time) nicely pullback/breakout fibo levels is because of the collective belief of a large number of technical traders in fibo levels (a self-fulfilling prophecy) if they collectively put their stops/limits there, but even that probably won't work because the professional participants, the big institutional players will trade on some other basis, and the breakdown/reversal of the Fibo level may be just random, but for believers in the EQ it will certainly be a confirmation of their faith.
Keith Devlin, Professor of Mathematics at Stanford University explains it simply: "..... Most people don't understand maths, and can't even understand how a formula like the golden ratio applies to a complex system, so they can't test themselves either. People think they see the golden ratio everywhere, in nature and in their favourite objects, but they can't substantiate it. They are victims of their natural desire to find meaning in the various objects of the universe, but because of their lack of mathematical literacy they cannot realise that the patterns they detect are illusory."
People programme themselves (zombie) to find a simple explanation and strive to maintain this belief, this is the essence of religious thinking, including in trading...
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
New article Combinatorics and probability theory for trading (Part II): Universal fractal has been published:
In this article, we will continue to study fractals and will pay special attention to summarizing all the material. To do this, I will try to bring all earlier developments into a compact form which would be convenient and understandable for practical application in trading.
Let's use the construction rules that we derived in the previous article, and supplement them to understand how a fractal is constructed. In addition, I have found a small mistake in my formulas, due to which downward or upward asymmetrization of borders was impossible. The derived formulas turned out to be correct, and thus they work for absolutely any fractal. Actually, this is a function for implementing absolutely any fractal. All possible fractals are a special case of a general fractal. If we take the three fractal types defined above, the conditions of the general fractal for the implementation of these three special cases will be as follows:
Schematically, these three types of fractals look like this:
Ideally, "S" should tend to infinity. The following variables were not described in my previous article. I will provide the relevant descriptions here to get a complete picture of how to use the general formula to get the special cases. A fractal is a function that works on the principle of a chain reaction, as in an atomic bomb. If the set chain reaction is too deep, the computer may fail to cope with such massive calculations. If the case is not particularly critical, it will simply count for a very long time — minutes, hours or even days.
Author: Evgeniy Ilin