如果可能的话,我请这篇文章的作者考虑以下论点:
到目前为止,我发现黄金比例原理可以用来构建分形-概率链,形成一组完整的事件,但说实话,我不知道这种方法能带来什么。黄金分割率似乎也与菲波数列有关,但我同样不知道它如何应用,又是为了什么,如果你有想法,可以写在这里,我想这将是一个加分项。因此,总的来说,这些过程已经在我的脑海中形成,一般来说,这就是推导更复杂公式所需要的一切。到目前为止,所得到的分形 已经完成了它们的任务。在这里,一切都从复杂变得简单,如此循环往复。我可以考虑应用黄金分割率,但我看不出它有什么用处。菲波数列也是,每个人都说菲波-菲波......奥洛洛,他们听到一个聪明的词,就会像鹦鹉一样重复。我总是从数学原理与特定问题相对应这一事实出发,并且总能在一段时间后找到任何问题的解决方案。在这个过程中,解决问题的工具会被选中,大脑会自己找到它,如果可能的话,还会找到与耳边事物的相似之处。换句话说,我们首先确定需要找到什么,然后再寻找解决问题的方法。我更想听听具体的问题,你可以单独写一篇文章介绍这些解决方案,我想那一定会很有趣、很好玩。在这些问题的框架内,我们可以应用黄金分割率,也可以应用其他任何东西,只要结果是真正必要的,并能给某个人带来具体的好处。所以,你可以写建议。
这只是一个老生常谈的神话,据说 fibo 和 ZS 无处不在,无时不有...
有趣的是,如果你拿起任何一个罐子并把它拧好,你就能在里面找到斐波、黄金分割率、π数、e数和其他许多东西....。
如果你把锅放在头上,你还能在锅里找到头和肩膀)。
菲波和 ZS 无处不在、无处不在,这只是一个老生常谈的神话....。
有趣的是,如果你拿起任何一个罐子并把它拧好,你就能在里面找到斐波和黄金分割率、圆周率、e 和许多其他东西....。
我完全同意 ))) 这确实是真的。交易者非常喜欢在没有意义的地方寻找隐藏的意义)。我也在努力向人们仔细传达同样的意思,但我不知道如何才能不说出真相,而真相是残酷的)。我的观点是,有一个问题,就有一套可能的解决方案,除此之外的任何东西都是浪费时间。为了得到一个解决方案,你必须首先清楚地设定问题,并至少对其可能的解决方法有一个肤浅的想法,如果没有这样的方法,那么就开始上面所说的,斐波那契、欧拉公式和其他非常美丽但无用的垃圾,以至于你不由自主地开始阅读字里行间。每种工具都有自己的任务。在这方面,我建议具体问题具体分析(具体任务)。
到目前为止,我看到黄金分割率原理可以用来构建分形概率链,形成一组完整的事件,但说实话,我不知道这种方法能做什么。黄金分割率似乎还与纤维数列有关,但我同样不知道它如何应用,又是为了什么,如果你有想法可以写在这里,我想这将是一个加分项。因此,总的来说,这些过程已经在我的脑海中形成,一般来说,这就是推导更复杂公式所需要的一切。到目前为止,所得到的分形 已经完成了它们的任务。在这里,一切都从复杂变得简单,如此循环往复。我可以考虑应用黄金分割率,但我看不出它有什么用处。菲波数列也是,每个人都说菲波-菲波......奥洛洛,他们听到一个聪明的词,就会像鹦鹉一样重复。我总是从数学原理与特定问题相对应这一事实出发,并且总能在一段时间后找到任何问题的解决方案。在这个过程中,解决问题的工具会被选中,大脑会自己找到它,如果可能的话,还会找到与耳边事物的相似之处。换句话说,我们首先确定需要找到什么,然后再寻找解决问题的方法。我更想听听具体的问题,你可以单独写一篇文章介绍这些解决方案,我想那一定会很有趣、很好玩。在这些问题的框架内,我们可以应用黄金分割率,也可以应用其他任何东西,只要结果是真正必要的,并能给某个人带来具体的好处。因此,你可以写一些建议。
1.也许每个人都听说过这个 "ololo",但我没有写斐波,因为我不建议 "拉伸 "斐波水平,尽管如果你计算正确,你可以使用它们,但要与艾略特波浪相结合。
当然,这还不是全部,你会意识到这项工作是多么费时费力,但我发起这个主题是有原因的。老实说,一般来说,这样的问题应该由整个数学家和程序员团队,甚至是整个研究所来解决。 一个人又能做什么呢?即使你有超级大脑,要处理的数据也多得让你抓狂。我正在努力设定那些与我的时间和能力相称的任务,是的,我可以做得更多,但现在并不取决于我。时间是最宝贵的资源。如果有人对复杂的分析感兴趣,并愿意全身心投入,我会很乐意去做。尽管如此,这个分支仍将继续,我将尽可能地介绍我所能介绍的材料,我总是在我力所能及的范围内尝试介绍一些新的东西。
关于黄金分割 率在自然界中普遍存在的神话越来越多,以至于人们甚至懒得进行真正的检查,而是屈从于整体与部分之比这一美丽理念的魅力,但事实上并非如此:
- 软体动物--鹦鹉螺的外壳(通常在有关 WD 神奇的文章中都有图解)与大众的看法相反,并不符合 WD。
- 达芬奇的著名画作 "维特鲁威人 "中的人体比例与真人不符。
- 帕台农神庙、金字塔和其他物体与 RS(由神秘主义爱好者绘制)不符。
- 旨在揭示情商是否是感知美的基础的客观心理学研究均以失败告终。
- 最后,对交易中的水平分解/拒绝进行的定量测试也没有表明 EQ 是特别重要的东西。
市场有时(关键词 "还有一次")能很好地回撤/突破纤维水平的唯一原因是,如果大量技术交易者集体将止损/限价设在纤维水平上,他们就会集体相信纤维水平(这是一个自我实现的预言),但即使这样也可能行不通,因为专业参与者、大型机构参与者会在其他基础上进行交易、斐波水平的击穿/反转可能只是随机的,但对于 EQ 的信徒来说,这无疑是对他们信仰的确认。
斯坦福大学数学教授 基思-德夫林(Keith Devlin)对此的解释很简单:".....。大多数人不懂数学,甚至无法理解黄金分割率这样的公式是如何应用于复杂系统的,因此他们也无法测试自己。人们认为自己在自然界和自己喜欢的物品中到处都能看到黄金比例,但他们无法证实这一点。他们是在宇宙的各种物体中寻找意义的自然欲望的牺牲品,但由于缺乏数学素养,他们无法意识到他们发现的模式是虚幻的"。
人们将自己(僵尸)设定为寻找一种简单的解释,并努力维持这种信念,这就是宗教思维的本质,包括在交易中......
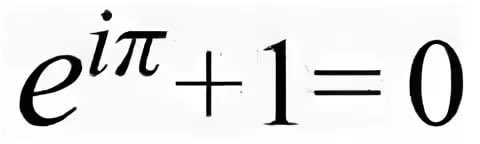
新文章 针对交易的组合数学和概率论(第二部分):通用分形已发布:
在本文中,我们将继续研究分形,并会特别留意总结所有材料。 为此,我将尝试把所有早期开发归纳为一个紧凑的形式,这对于交易中的实际应用来说将是方便和易于理解的。
我们运用在上一篇文章中导出的构造规则,并对其进行补充,从而了解分形是如何构造的。 此外,我在我的公式中发现了一个小错误,因为向下或向上的边界不对称是不可能的。 结果证明导出的公式是正确的,因此它们绝对适用于任何分形。 实际上,这个函数能绝对实现任何分形。 所有可能的分形都是一般分形的特例。 如果我们取上面定义的三种分形类型,那么实现这三种特殊情况的一般分形的条件如下:
示意性地,这三种类型的分形如下所示:
理想情况下,“S” 应该趋于无穷大。 以下变量在我之前的文章中并未讲述。 我将在此处提供相关说明,从而能全面了解如何运用通用公式来得到特殊情况。 分形是根据链式反应原理工作的函数,就像在原子弹中一样。 如果设置的连锁反应太深,计算机可能无法应对如此庞大的计算。 如果情况不是特别严重,它简单地花费很长时间来计算 — 几分钟、几小时、甚至几天。
作者:Evgeniy Ilin