Perché ci sono questi trucchi con le lauree? - pagina 2

[Andrey Azatskiy]

Roman:

-0,2 non è zero per restituire un errore di divisione per zero.

La funzione restituisce -nan, cioè Not a Number. e l'errore viene lanciato quando si cerca di dividere per -nan. Semmai, il testo dell'errore è semplicemente inadeguato.

[[Eliminato]]

Soluzione corretta: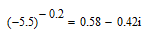 soluzione è nel dominio complesso.

Ma se stiamo parlando di avere diversi rami di soluzioni per parametri di input positivi e negativi, dobbiamo solo definire prima questi rami:

.

Fate una tale caratteristica e sarete a posto ;)

[Roman]

Andrey Azatskiy:

La funzione restituisce -nan, cioè Not a Number. e viene lanciato un errore quando si cerca di dividere per -nan. Semmai, il testo dell'errore è semplicemente inadeguato.

Perché mai -0,2 dovrebbe essere -nan ?)

Un'altra funzione di test

In calcolatrice.

1/(-3 ^ 3)

-27

Nelle funzioni mql

double n = 1.0/MathPow(-3.0, 3.0);
Print(n);

-0.03703703703703703

[Andrey Azatskiy]

Roman:

Allora perché diavolo è -0,2 un nan?)

Un'altra funzione di test

In una calcolatrice

In una funzione mql.

non è -0,2 - nan, ma il risultato di un aumento di grado.
Il grado frazionario di un numero (a^m/n) è la radice di grado n di a^m.
Se il valore della radice secondaria è negativo, può essere negativo o positivo, in base alla potenza di m e al numero a stesso (che nel mio problema è sempre negativo, quindi è positivo alla potenza positiva di m e negativo alla potenza negativa). Quindi se il valore della radice secondaria è negativo, anche il numero è negativo. La radice di un numero negativo si trova nell'area complessa, quindi non possiamo operare su valori dell'area complessa tramite il solitotipo doppio, che è il motivo per cui l'implementazione standard del grado dà -nan.

[Andrey Azatskiy]

Олег avtomat:

Soluzione corretta: la soluzione è nel dominio complesso.

Ma se stiamo parlando di avere diversi rami di soluzioni per parametri di input positivi e negativi, allora abbiamo solo bisogno di definire questi rami prima:

.

Fate una tale funzione e tutto andrà bene ;)

Grazie per la sua risposta dettagliata. Ma per me il calcolo complesso non è adatto al mio problema, quindi molto probabilmente mi limiterò ai numeri naturali e di conseguenza non cadrò nel dominio complesso.

[[Eliminato]]

Andrey Azatskiy:

Grazie per la sua risposta dettagliata. Ma per me il calcolo complesso non è adatto al mio problema, quindi probabilmente mi limiterò ai numeri naturali e di conseguenza non cadrò nell'area complessa.

È di questo che sto parlando, e ti ho mostrato specificamente un esempio. Guardate attentamente. Questo esempio è esattamente per il tuo caso.

zy

tradurre in µl è molto facile

[Roman]

Andrey Azatskiy:

non è -0,2 - nan, ma il risultato di un grado.
La potenza di un numero frazionario (a^m/n) è la radice di grado n di a^m.
Se il valore della sotto-radice è negativo, può essere negativo o positivo in base alla potenza di m e al numero a stesso (che nel mio problema è sempre negativo, quindi è positivo a potenza positiva di m e negativo a negativa). Quindi se il valore della radice secondaria è negativo, anche il numero è negativo. La radice di un numero negativo si trova nell'area complessa, quindi non possiamo operare su valori dell'area complessa tramite il solito tipo doppio, che è il motivo per cui l'implementazione standard del grado dà -nan.

Andrey, sì, mi sono espresso male, è chiaro che il risultato dell'elevazione a una potenza restituisce -nan.
Ma questo risultato dà luogo a una potenza frazionaria, dove l'intero è zero -0,2
La calcolatrice calcola tutto correttamente.

E anche il test precedente non conta come nella calcolatrice.

[Andrey Azatskiy]

Олег avtomat:

È di questo che sto parlando, e ti ho fatto un esempio specifico. Guardate bene.

Sì, ho capito, grazie. (anche una formula è scritta)

[Aleksey Nikolayev]

Andrey Azatskiy:

Forse le gambe nascono dal fatto che non si può prendere una radice pari da un numero negativo? Sono già un po' confuso... E soprattutto come aggirarlo?

I gradi interi sono determinati semplicemente dalla moltiplicazione (e prendendo l'inverso per gli esponenti negativi), quindi sono facilmente trasferiti alle basi negative. I gradi frazionari sono definiti tramite logaritmo ed esponente: y^x=exp(x*ln(y)) e con i numeri negativi arrivano al piano complesso. Il logaritmo ha un numero infinito di rami e per evitare il fastidio di trovare il ramo giusto, restituiscono NAN.

[Igor Makanu]

Andrey Azatskiy:

Grazie per la tua risposta, ma in generale se prendiamo una soluzione aritmeticamente corretta, sembra che solo i numeri complessi possano essere usati per implementare tale soluzione... Nel metodo da voi proposto è necessario rompere il grado in modo che il valore sottostante abbia sempre un grado positivo e la risposta sarà sempre positiva. Ma se si prende senza questo adattamento - si arriva solo ai numeri complessi, infatti secondo il modello algebrico generalmente accettato che io sappia (non sono un matematico di formazione) - la radice di un numero negativo sarà un numero complesso.

utilizzare la formula che ho suggerito sopra.

Ecco la stessa formula:

void OnStart()
  {
   int m = 2;
   int n = 10;
   
   double result = 1.0/pow(pow(-5.5,m),1.0/n); 		// result = 0.7110947333604484
   Print("result = ",result);
  }

ed ecco un esempio di come convertire un doppio in una frazione

https://www.mql5.com/ru/forum/290279#comment_9396706