Denis, j'ai ce commentaire sur l'article.
En ce qui concerne la théorie, il n'y a pas de questions, tout est présenté en détail.
En ce qui concerne la pratique, j'aimerais attirer votre attention sur les figures où vous montrez des histogrammes empiriques, en particulier la figure 2. Le fait est que vous avez commis deux inexactitudes très importantes dans votre analyse.
Premièrement, vous avez défini un nombre trop faible de classes pour le script générant les histogrammes - seulement 9, ce qui, en soi, porte un coup énorme à la puissance du critère de Pearson et rend son application inefficace. À l'avenir, prenez 200-300 classes pour être sûr, bien sûr, que si la taille de l'échantillon le permet (et c'est le cas), vous ne ferez pas d'erreur. Si vous aviez fait exactement cela, vous auriez pu vous assurer que le test de distribution lognormale aurait donné un résultat négatif, ainsi que le test de rendement pour les hypersécans. D'ailleurs, il est très facile de s'assurer que deux distributions de ce type ne peuvent pas représenter simultanément une certaine valeur et son module, il suffit de prendre la "moitié" de l'hypersécance et de la convoluer avec elle-même (analogue à la prise du module d'une variable aléatoire) : vous n'obtiendrez certainement pas une distribution lognormale.
La deuxième inexactitude est que vous n'avez pas utilisé la connaissance a priori selon laquelle le sommet (ou l'espérance) de la distribution des rendements doit être exactement à 0 (sinon nous serions tous milliardaires depuis longtemps). C'est pourquoi l'histogramme de la figure 2 semble décalé vers la droite, alors qu'il ne devrait pas l'être. Une fois encore, la prise en compte de ce facteur lors du tracé de l'histogramme rendrait les tests plus fiables.
P.S. Je suis en train d'écrire un article sur les bases de la modélisation, d'où un intérêt aussi vif. Merci pour votre article, il est dans le sujet. Cordialement.
...Tout d'abord, vous avez défini un nombre trop faible de classes pour le script générant les histogrammes - seulement 9, ce qui en soi est un gros coup porté à la puissance du critère de Pearson et rend son application inefficace. À l'avenir, prenez 200-300 classes pour être sûr, bien sûr, que si la taille de l'échantillon le permet (et c'est le cas), vous ne ferez pas d'erreur. Si vous aviez procédé ainsi, vous auriez pu vous assurer que le test de distribution lognormale donnerait un résultat négatif, de même que le test de rendement pour les hypersécans. D'ailleurs, il est très facile de s'assurer que deux distributions de ce type ne peuvent pas représenter une certaine valeur et son module en même temps, il suffit de prendre la "moitié" de l'hypersécance et de la convoluer avec elle-même (analogue à la prise du module d'une valeur aléatoire) : vous n'obtiendrez certainement pas une distribution lognormale.
Cher alsu, merci pour votre avis !
Reprenons dans l'ordre.
Le nombre de classes n'est pas fixé volontairement, mais selon une formule. Dans mon cas, il s'agit de la formule de Sturgis. C'est l'une des règles les plus populaires. Elle n'est pas parfaite, j'en conviens. Mais tout de même...
Et vous prenez 200-300 classes selon quelle règle ?
La deuxième inexactitude est que vous n'avez pas utilisé la connaissance a priori que le sommet (aka expectation) de la distribution des rendements doit être exactement à 0 (sinon nous serions tous milliardaires depuis longtemps). C'est pourquoi l'histogramme de la figure 2 semble décalé vers la droite, alors qu'il ne devrait pas l'être. Là encore, la prise en compte de ce point lors de la construction de l'histogramme rendrait les tests plus fiables.
J'analyse l'échantillon sur une base factuelle. J'analyse ce que j'ai. Et sur quelle base le sommet de la distribution des rendements devrait-il se situer exactement au point 0 ? Peut-être ai-je mal compris quelque chose...
De plus, si vous regardez la distribution pour laquelle l'ajustement a été mis en œuvre (qui était X~HS(-0,00, 1,00)), il est facile de voir que le premier paramètre - le paramètre de décalage - est exactement égal à 0. En fait, il est égal à l'espérance.
Voici un autre rapport html sur l'échantillonnage des valeurs standard. J'espère que la figure est plus ou moins lisible. Mais elle n'est pas identique à celle de l'article. J'ai pris les dernières données à l'instant.
Comme vous pouvez le voir, la moyenne =0. Et le meilleur ajustement est la distribution de la sécante hyperbolique : X~HS(0.00, 1.00).
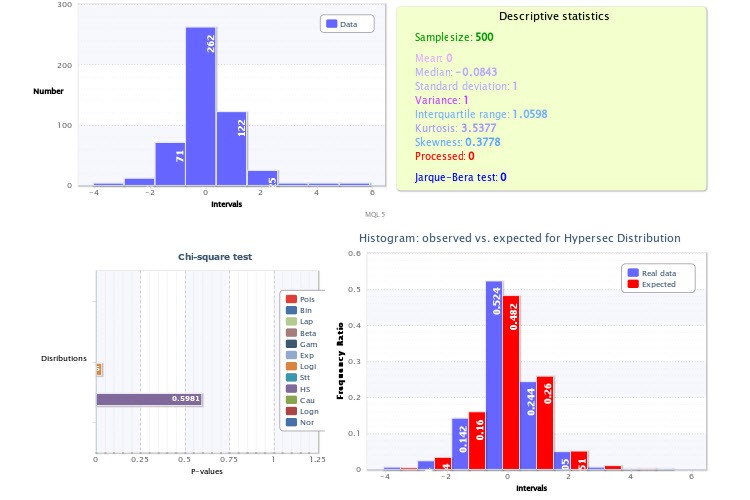
Exactement, la formule de Sturges donne exactement 9 classes, mais c'est plutôt une raison pour penser à augmenter la taille de l'échantillon (en inversant la formule, je vois que vous l'avez autour de 256 ?).
En outre, cette formule ne fonctionne bien que pour des populations générales de distribution normale (pour lesquelles elle a été dérivée) et, comme on le considère, la taille de l'échantillon n'est pas supérieure à 200 valeurs. Vous pouvez utiliser d'autres formules - Diakonis, Scott....
En général, vous savez, Sturges n'a jamais donné de justification logique de sa formule - oui, elle est basée sur l'approximation de la distribution normale par la distribution binomiale, et alors ? Comment cela peut-il affecter la question de l'efficacité du choix du nombre de classes ? Le critère d'optimalité n'a jamais été défini par l'auteur et la formule elle-même a été écrite au hasard. Mais le fait est que l'approche de Sturges a longtemps été la seule formalisée, et qu'elle a été automatiquement (et, à mon avis, assez inconsidérément !) incluse dans tous les logiciels statistiques, ce qui, soit dit en passant, est assez ennuyeux, précisément parce que cette formule donne presque toujours un nombre de classes extrêmement sous-estimé.
Encore une fois, il existe des formules alternatives, mais c'est la présence d'un ordinateur personnel qui, paradoxalement, nous donne la possibilité d'utiliser notre propre tête comme un appareil, c'est-à-dire un moyen visuel de déterminer un nombre de classes plus ou moins optimal pour cet échantillon particulier, lorsque, en modifiant en douceur cet indicateur, nous obtenons un compromis entre la douceur du graphique et la résolution de l'histogramme. Soit dit en passant, cette méthode est souvent meilleure et plus rapide que n'importe quelle formule.
Je dis toujours à tout le monde qu'avant de mettre des chiffres dans des formules, il faut se demander ce que cela signifie et comment (et si) il faut l'appliquer. En bref, je suis contre l'utilisation de la formule de Sturges, que je considère comme dépassée et inadéquate).
En ce qui concerne la moyenne. L'espérance de rendement devrait être à 0 car si ce n'était pas le cas, on pourrait stupidement parier toujours dans une direction, correspondant au signe de ce MO, et être assuré d'obtenir un rendement de n'importe quelle taille prédéterminée. Le sommet devrait coïncider avec le MO uniquement pour des raisons de symétrie : la moitié gauche du graphique devrait être une image miroir de la moitié droite (les taux d'augmentation et de diminution sont statistiquement égaux et il ne devrait pas y avoir de différences entre eux), de sorte que le centre de symétrie coïncide avec le centre.
Puisque vous prenez HS(0,00, 1,00), vous devez donc centrer les classes - c'est-à-dire que la classe zéro doit inclure les valeurs de l'indice dans un intervalle symétrique (-x0;x0), sinon nous introduisons dans les calculs une erreur systématique associée au décalage des classes par rapport à zéro, qui finit par se glisser dans le résultat du test du chi^2. Votre point 0 n'est pas au milieu de la classe zéro.
En fait, la question de savoir comment rendre les classes symétriques sur des données discrètes n'est pas triviale et, encore une fois, il est bon de la résoudre pour chaque échantillon particulier individuellement et très soigneusement, sinon nous risquons d'obtenir un résultat inadéquat également en raison du mauvais choix des limites de la division en classes.
alsu, vous avez abordé un sujet qui, bien que ne faisant pas l'objet de mon article, est extrêmement intéressant. Dans la mesure du possible, je ferai des recherches plus approfondies sur cette question.
Je vous remercie pour votre critique constructive !
J'apprécie votre opinion sur l'applicabilité des connaissances scientifiques au commerce.
Pourriez-vous me dire quels sont les livres que vous recommanderiez à une personne qui connaît la théorie des probabilités et les statistiques mathématiques ?
Denis, bonjour.
J'apprécie votre opinion sur l'applicabilité des connaissances scientifiques dans le domaine du commerce.
Veuillez me dire quels sont les livres que vous recommanderiez à une personne qui connaît la théorie des probabilités et les statistiques mathématiques.
Je vous remercie pour votre avis !
Je pense qu'il faut chercher quelque chose pour les débutants, un petit rôle. L'essentiel est que le texte du livre ne vous décourage pas de le lire plus avant :-))).
J'ai aimé quelque chose de Gaidyshev, et quelque chose de Bulashev.....
Il y a un fil de discussion intéressantici.
- rsdn.org
La deuxième inexactitude est que vous n'avez pas utilisé la connaissance a priori selon laquelle le sommet (ou l'espérance) de la distribution des rendements doit être exactement à 0 (sinon nous serions tous milliardaires depuis longtemps).
Ce n'est pas du tout le cas. Un déplacement du sommet de la distribution par rapport à 0 (croissance/décroissance d'un instrument) ne signifie pas qu'il en sera de même à l'avenir. C'est la raison pour laquelle la plupart des traders ne sont pas milliardaires, et non pas parce qu'ils sont milliardaires.
Merci de votre attention.
...Le fait de déplacer le sommet de la distribution par rapport à 0 (instrument en hausse ou en baisse) ne signifie pas nécessairement que ce sera le cas à l'avenir...
Je suis d'accord.
Question pour alsu. Parliez-vous de l'efficience du marché lorsque vous évoquez le point zéro ?
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Un nouvel article Le Rôle des Distributions Statistiques dans le Travail des Traders a été publié :
Cet article est la suite logique de mon article Statistical Probability Distributions en MQL5 qui présente les classes pour travailler avec certaines distributions statistiques théoriques. Maintenant que nous disposons d'une base théorique, je suggère que nous procédions directement à des ensembles de données réelles et que nous essayions de faire un usage informatif de cette base.
Nous afficherons l'histogramme à l'aide des outils décrits dans les HTML. Pour cela j'ai écrit la fonction histogramSave qui affichera l'histogramme de la série à l'étude en HTML. La fonction prend 2 paramètres : un tableau de classes et (f) un tableau de milieux de classes(b).
À titre d'exemple, j'ai créé un histogramme pour les différences absolues entre les maximums et les minimums de 500 barres de la paire EURUSD sur une plage de quatre heures en points à l'aide du script volatilityTest.mq5
Figure 1. Histogramme des données (volatilité absolue de l' EURUSD H4)
Auteur : Denis Kirichenko