- Loss functions
- Error gradient backpropagation method
- Methods for optimizing neural networks
Methods for optimizing neural networks
We continue to move forward in studying the basic principles of neural network training. In previous chapters, we have already discussed various loss functions and the error gradient backpropagation algorithm, which allows us to determine the influence of each neuron on the overall result and the direction of change in the output value of each neuron to minimize the overall error at the output.
Below is the formula of the mathematical model of a neuron.
Where:
- f = activation function
- n = number of elements in the input sequence
- wi = weight of the ith element of the sequence
- xi = ith element of the input sequence
Gradient descent and stochastic gradient descent #
In the above formula, you can see that the output value of the neuron depends on the activation function, the input sequence, and the weight vector. The activation formula is set during the construction of the neural network and remains unchanged. The neuron does not affect the input sequence. Therefore, in the learning process, we can change the value at the output of the neuron only by choosing the optimal values of the weights.
The rate of change of the neuron's output value when changing a particular weight is equal to the partial derivative of the neuron's mathematical model function with respect to that weight. From this, to get the delta change of a particular weight, you need to multiply the error at the neuron's output in the current situation by the partial derivative of the neuron's mathematical model with respect to that weight.
It should be noted that the function of the mathematical model of a neuron most often is non-linear. Therefore, the partial derivative is not constant over the entire permitted range of values. Therefore, the "learning coefficient" parameter is introduced into the formula for updating the weights, which determines the learning rate.
The approach described above is called gradient descent. In general, it can be expressed by the formula:
where:
- wjil = lth weight on the ith neuron of the jth layer
- α = learning coefficient that determines the learning rate
- gradij = gradient at the output of the ith neuron of the jth layer
The training coefficient α is a hyperparameter that is selected during the neural network validation process. It is selected from the range 0 to 1. In this case, the training coefficient cannot be equal to the extreme values.
When α=0, there will be no learning, because by multiplying any gradient by zero, we always get zero for updating the weights.
When α=1 or close to this value, there is another problem. If, when moving towards the error minimum, the value of the partial derivative decreases, then using a sufficiently large step will throw us past the minimum point. In the worst case, the error at the output of the neural network will even increase. Moreover, a large learning coefficient promotes maximum adaptation of the network to the current situation. In this case, the ability to generalize is lost. Such training will not be able to identify key features and adequately work "in the field."
The method works well with small neural networks and datasets. But neural networks are getting bigger, and training sets are growing. To make one training iteration, you need to perform a forward pass through the entire dataset and save information about the state of all neurons for all samples as this information will be needed for the backward pass. Consequently, we will need additional memory allocation in the amount of the number of neurons * the number of data sets.
The solution was found in the use of stochastic gradient descent. The method retains the algorithm of standard gradient descent, but the weights are updated for each randomly selected data set.
On each iteration, we randomly select one data set from the training sample. Then we perform a forward and backward pass and update the weights. After that, we "shuffle" the training sample and select the next data set randomly.
We repeat the iterations until we achieve an acceptable error in the neural network output.
Stochastic gradient descent has lower convergence compared to standard gradient descent. Furthermore, more iterations are usually required to achieve an acceptable error. But in stochastic gradient descent, a single iteration takes less time, since it is carried out on a randomly chosen data set, rather than on the entire sample, as in standard gradient descent. In general, the process of training a neural network is carried out with less time and resource costs.
Below is an example of implementing a function to update weights using the gradient descent method. In parameters, the function receives two pointers to data arrays (current weights and gradients to them) and a training coefficient. First, we check the correspondence of the sizes of the arrays. Then, we organize a loop where for each element of the weight array, we calculate a new value using the formula mentioned above. The obtained value is saved in the corresponding cell of the array.
bool SGDUpdate(double &m_cWeights[], |
Momentum accumulation method #
Probably, the main drawback of gradient descent methods is the inability to distinguish between local and global minima. During the training process, there is always a high risk of stopping at a local minimum without reaching the desired accuracy level of the neural network.
Careful selection of the learning coefficient, experiments with different weight initialization options, and several training iterations do not always yield the desired results.
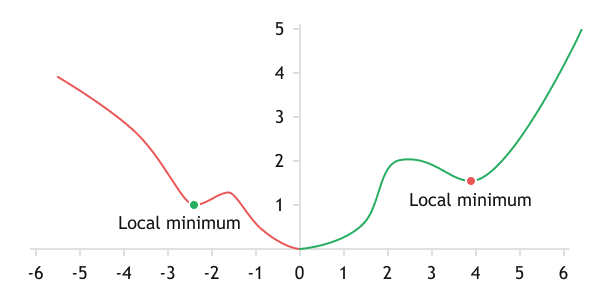
Local minima on the graph of a complex function
One of the solutions was borrowed from the physics of natural phenomena. If you put the ball in a small depression or hole, then it will lie motionless at its bottom. But as soon as we send the same ball along some inclined surface into this hole, it will easily jump out of it and roll further. This behavior of the ball is explained by the momentum accumulated during the descent along the inclined surface.
Similar to the ball, it was suggested to accumulate momentum during the training of the weights, and then add this momentum to the weight update formula using the gradient descent method.
Momentum accumulates for each individual weight. When updating a specific weight for a prolonged period in one direction, its momentum will accumulate, and as a result, it will move towards the desired goal at a faster pace. Thanks to the accumulated energy, we can overcome local minima, similar to a ball rolled down an inclined surface.
Unfortunately, there is also a flip side to the coin. By accumulating momentum, we will skip not only the local minimum but also the global one. With unlimited momentum accumulation, the value of our error will move like a pendulum on the loss function graph. Let's mimic the force of friction in nature and add the β coefficient in the range from 0 to 1 (excluding the boundary points), which will serve the role of frictional force. This coefficient characterizes the rate of momentum attenuation. The closer β is to 1, the longer the momentum is maintained.
All of the above can be written in the form of two mathematical formulas:
where:
- Δt = change in the weight at the current step
- Δt–1 = change in the weight at the previous training iteration
- β = pulse damping factor
As a result, we got a decent algorithm for dealing with local minima. Unfortunately, it is not a panacea. To overcome the local minimum, you need to accumulate enough momentum. To do this, the initialization must be at a sufficient distance from the local minimum. When solving practical problems, we do not know where the local and global minima actually are. And the initialization of weights in a random way can throw us anywhere.
Moreover, the application of this method requires additional memory to store the last momentum of each neuron and extra computational effort for the added calculations.
Still, the momentum accumulation method is used in practice and demonstrates better convergence compared to stochastic gradient descent.
When implementing the momentum accumulation method, we will need to add a decay coefficient to the function parameters and another array to store the accumulated momentum for each weight. The logic of building the function remains the same: first, we check the correctness of the input data, and then in a loop, we update the weights. When updating the weights, as in the provided formulas, we first calculate the change in the synaptic coefficient taking into account the accumulated momentum, and then its new value. The obtained values are stored in the corresponding cells of the arrays for weights and momentum values.
bool MomentumUpdate(double &m_cWeights[], |
//--- |
Adaptive gradient method (AdaGrad) #
Both methods discussed above have a learning rate hyperparameter. It is important to understand that the entire process of neural network training largely depends on the choice of this parameter. Setting the learning rate too high can cause the error to continually increase instead of decreasing. Using a low learning rate will lead to an extended duration of the training process and increase the likelihood of getting stuck in a local minimum, even when using the momentum accumulation method.
Therefore, when validating the architecture of a neural network, a lot of time is devoted specifically to selecting the correct learning rate coefficient. Furthermore, it is always difficult to select the right learning rate. Moreover, one always wants to train a neural network with minimal time and resource expenditures.
There is a practice of gradually decreasing the learning rate during the training process. The network training process starts with a relatively high rate, which allows for a rapid descent to a certain error level. After reducing the learning rate, a more refined adjustment of the neural network weights is carried out to reduce the overall error. There can be several iterations with a reduced coefficient, but with each reduction of the weight, the effectiveness of that iteration decreases.
Note that we use one learning rate for all neural layers and neurons. However, not all features and neurons contribute equally to the final result of the neural network, so our learning rate should be quite versatile.
I think it goes without saying that universality is the enemy of the best: to create any universal product or select a value (as in our case), we need to compromise to meet all the requirements as best as possible, while these requirements are often contradictory.
One might think, in such a case, it would be advisable to offer individual learning rates for neurons. But to solve this problem manually is virtually impossible. In 2011, the AdaGrad adaptive gradient method was proposed. The proposed method is a variation of the gradient descent discussed above and does not exclude the use of the learning rate coefficient. At the same time, the authors of the method suggest accumulating the sum of the squares of the gradients for all previous iterations and, when updating the weights, dividing the learning coefficient by the square root of the accumulated sum of the squared gradients.
Where:
- Gt , Gt–1 = sum of the squares of the gradients at the current and previous steps, respectively
- ε = a small positive number to avoid division by zero
In this way, we obtain an individual and constantly decreasing learning rate coefficient for each neuron. However, this requires additional computational resources and extra memory to store the sums of squared gradients.
The implementation function for the AdaGrad method is very similar to the function of updating the weights using the cumulative momentum method. In it, we abandon the use of the decay coefficient but still use the momentum array, in which we will accumulate the sum of squared gradients. The changes also affected the calculation of the new weight value. The complete function code is shown below.
bool AdaGradUpdate(double &m_cWeights[], |
//--- |
In the above formula, you can notice the main problem of this method. We continuously accumulate the sum of squared gradients. As a consequence, on a sufficiently long training sample, our learning rates will quickly tend to zero. This will lead to the paralysis of the neural network and the impossibility of further training.
A solution was proposed in the RMSProp method.
RMSProp method #
The RMSProp weight update method is a logical extension of the AdaGrad method. It retains the idea of automatically adjusting the learning rate based on the frequency of updates and the magnitude of gradients coming to the neuron. However, it addresses the main issue of the previously discussed method — the paralysis of training on large training datasets.
Like AdaGrad, the RMSProp method exploits the sum of squared gradients, but in RMSProp, an exponentially smoothed average of squared gradients is used.
Where:
- REMS(G)t and REMS(G)t–1 = exponential average of the squares of the gradients at the current and previous iteration
- γ = exponential smoothing factor
The use of an exponentially smoothed average of squared gradients prevents the learning rate of neurons from decreasing to zero. At the same time, each weight will receive an individual learning rate, depending on the incoming gradients. As the gradients increase, the learning rate will gradually decrease, and as the gradients decrease, the learning rate coefficient will increase. This will allow in the first case to limit the maximum learning rate, and in the second case, to update the coefficients even with small error gradients.
It should be noted that the use of the squared gradient allows this method to work even when the neuron receives gradients of different directions. If we skip over the minimum because of the high learning rate during the training process and move in the opposite direction on the next iteration, the accumulated square of gradients will gradually decrease the learning rate, thereby allowing us to descend closer to the minimum error.
The implementation of this approach almost completely repeats the implementation of the adaptive gradient method. We will simply replace the calculation of the sum of squared gradients with their exponential average. To do this, we need an additional parameter γ.
bool RMSPropUpdate(double &m_cWeights[], |
//--- |
Adadelta method #
In the AdaGrad and RMSProp methods, we gave an individual learning rate to each neuron, but still left the learning rate hyperparameter in the numerator of the formula. The creators of the Adadelta method went a little further and proposed to completely abandon this hyperparameter. In the mathematical formula of the Adadelta method, it is replaced by the exponential average of changes in weights over the previous iterations.
Where:
- REMS(δw)t , REMS(δw)t–1 = exponential average of squared changes in weights for the current and previous iterations
In the practical application of this method, you may encounter cases where both the coefficients for the exponential smoothing of squared weight deltas and gradients are the same, as well as cases where they are individual. The decision is made by the neural network architect.
Below is an example of the implementation of the method using MQL5 tools. The logic behind constructing the algorithm fully replicates the functions presented above. The changes only affected the calculations that are peculiar to the method: the abandonment of the learning rate and the introduction of an additional averaging coefficient, along with another array of data.
bool AdadeltaUpdate(double &m_cWeights[], |
//--- |
Adaptive moment estimation method #
In 2014, Diederik P. Kingma and Jimmy Lei Ba proposed Adam's adaptive moment assessment method. According to the authors, the method combines the advantages of the AdaGrad and RMSProp methods and works well in online learning. This method consistently demonstrates good results on various datasets and is currently recommended as the default choice in various packages.
The method is based on the calculation of the exponential average of the gradient m and the exponential average of the squares of the gradient v. Each exponential average has its own hyperparameter ß, which determines the averaging period.
The authors suggest using the default ß1 at the level of 0.9, and ß2 at the level of 0.999. In this case, m0 and v0 take zero values. With the parameters of the formulas presented above, at the beginning of training, they return values close to zero. As a consequence, we get a low learning rate at the initial stage. To speed up learning, the authors proposed to correct the obtained moments.
The updating of parameters is carried out by adjusting them based on the ratio of the corrected gradient moment m to the square root of the corrected gradient moment v. To eliminate division by zero, the ε constant close to zero is added to the denominator. The resulting ratio is corrected by the learning factor α, which in this case is the upper limit of the learning step. By default, the authors suggest using α at the level of 0.001.
The implementation of the Adam method is a little more complicated than the ones presented above, but in general it follows the same logic. Changes are visible only in the body of the weight update loop.
bool AdamUpdate(double &m_cWeights[], |
w -= learningRate * m / (MathSqrt(v) + 1.0e-10); |