Je ne vois pas de décalage dans le muving. Cela signifie que l'auteur ne comprend pas ce qu'il a défini, ou qu'il y a une erreur dans l'algorithme et que l'indicateur se redessine.
Il n'y a pas de décalage, car ce n'est pas un muwink en général. Le problème de la minimisation de la fonction pour une série donnée est résolu. Bien sûr, lorsque la série est en mouvement, si la longueur de la série est petite, elle se redessinera lorsque de nouvelles informations apparaîtront, surtout s'il y a des pics. Description du filtre sur http://en.wikipedia.org/wiki/Hodrick-Prescott_filter
En principe, cette fonction est dans MATLAB, si je ne me trompe pas, elle peut être transformée en DLL en utilisant le compilateur Matlab. Par conséquent, créez un indicateur qui répondrait à cette Dll.
Je pense que le monde est plus simple qu'avec un dll.
Voici la fonction que nous devons minimiser pour construire ce filtre numérique :
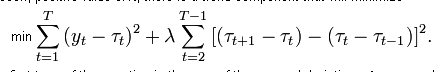
Nous pouvons voir que dans cette formulation, le filtre ne peut fonctionner que sur des données historiques, puisque pour calculer la valeur de la ligne de tendance à l'instant présent, nous devons connaître non seulement les valeurs précédentes de cette tendance mais aussi un pas en avant t[i+1]. Un tel filtre montrera, sur l'historique, la coïncidence exacte de la courbe lisse avec le kotir (c'est ce que l'auteur a cité dans le premier post comme démonstration), alors qu'à la limite droite du kotir il y aura un surdimensionnement incroyable.
Voici ce que j'ai trouvé d'autre sur le web :
Je n'ai pas trouvé de recette toute faite pour construire ce filtre. En fait, prenons et construisons nous-mêmes une fonctionnelle pour le bord droit de BP (équation supérieure).
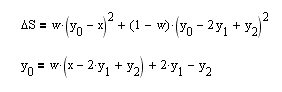
Prenons une dérivée de celle-ci par le paramètre y[0] - valeur actuelle et assimilons-la à zéro, et obtenons immédiatement une expression récurrente pour le filtre HP requis (équation inférieure). Voyons comment les propriétés de lissage du filtre dépendent du paramètre de lissage w :
Ici, la ligne verte est cotière, la ligne noire est w=0,5, etc. Vous pouvez voir que tout fonctionne correctement - il y a un décalage de phase inévitable qui est d'autant plus grand que l'anticrénelage est fort et le bord droit n'est pas redessiné. Maintenant, nous pouvons le coder en MQL également.
//+------------------------------------------------------------------+
//| Moving Average HP.mq4 |
//| Code by Neutron |
//+------------------------------------------------------------------+
#property indicator_chart_window
#property indicator_color1 Blue
#property indicator_width1 3
extern double w=0.1;
int Start,i,m;
double MA[5000],Y[5000];
int start()
{
Start=5000;
MA[Start]=Open[Start];
MA[Start-1]=Open[Start-1];
for (i=Start-2;i>=0;i--) MA[i]=w*(Open[i]-2.*MA[i+1]+MA[i+2])+2.*MA[i+1]-MA[i+2];
}
int init()
{
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,MA);
return(0);
}
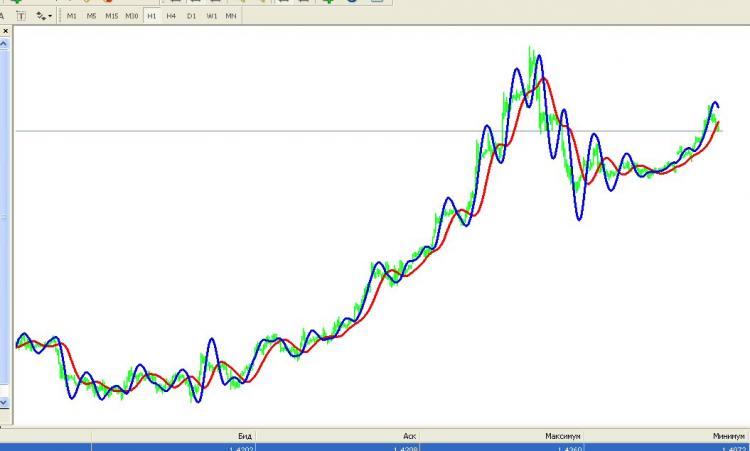
Voici comment ça s'est passé :
Le bleu est HP, le vert est cotier, le rouge est un filtre Watterout de 2ème ordre (pour comparaison).
En effet, ce filtre tente d'attraper honnêtement les tendances linéaires. Regardez la fonctionnalité en haut du post - elle montre qu'en plus de minimiser l'écart muving par rapport au kotir (première somme), il est nécessaire de minimiser la dérivée seconde (deuxième somme) ! Et après tout, la dérivée seconde de la ligne est nulle, et l'exigence de la minimiser est égale à l'exigence de maximiser l'aspiration à la ligne de tendance pour un vecteur d'entrée de données arbitraire. J'ai aimé l'approche.
P.S. Il est intéressant de noter que si, dans l'expression de la fonctionnelle, nous exigeons la minimisation de la première dérivée (l'équation supérieure) au lieu de la seconde, nous obtenons une formule de récurrence pour la moyenne exponentielle EMA (l'équation inférieure) :
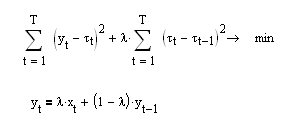
Il s'avère que la moyenne exponentielle est la plus lisse de toutes les muvings possibles !
Il s'avère que la moyenne exponentielle est la plus lisse de toutes les muwings possibles.
Oui, il existe un article sur le sujet.
Je n'ai pas fait sur l'article, mais en développant la même idée de lissage ema vous pouvez obtenir un bon lissage :
Bleu - EMA15 avec un retard de 5.
Rouge - MA plus fluide avec le même décalage.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation

Bonjour, chers programmateurs !
Qui entreprendra de résoudre, je pense, la simple tâche de rédiger un indicateur ? J'ai besoin d'écrire un indicateur qui filtrerait les séries avec le filtre Hodrick-Prescott. La fonction est disponible dans MATLAB, si je ne me trompe pas, elle peut être transformée en DLL à l'aide du compilateur MATLAB. Par conséquent, nous devons créer un indicateur qui s'adresse à cette Dll. A l'entrée, nous devons introduire les paramètres suivants - longueur de la série, paramètre de lissage. La sortie est une composante de tendance (à dessiner sur le graphique) et une composante cyclique (oscillateur).
Je ne peux pas le faire moi-même ; je ne connais pas le compilateur MATLAB et MQL4.
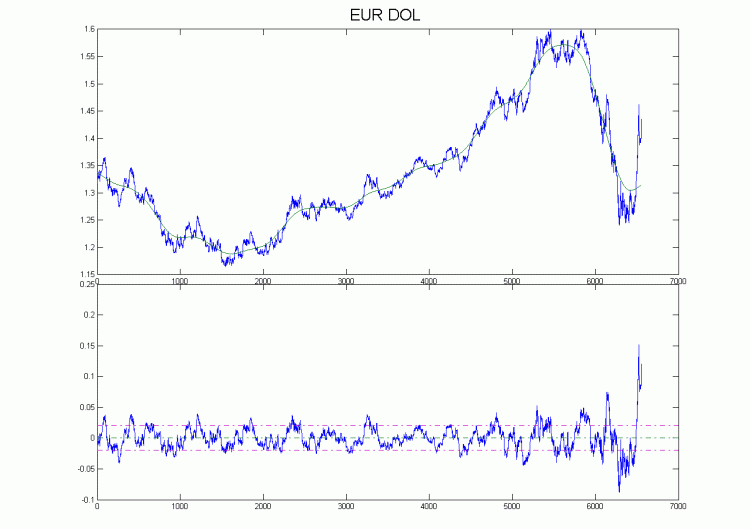
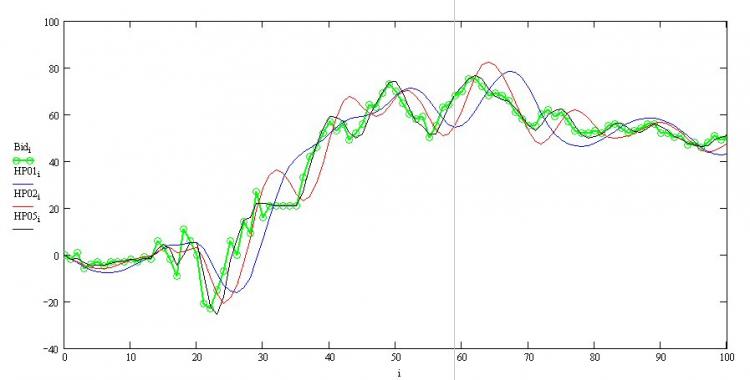
J'ai une décomposition pour Eurodollar H4 sur le graphique. Comme on l'a vu presque tout au long de l'histoire, la particularité du mouvement des prix était qu'après avoir cassé la tendance, le prix se déplaçait à une distance égale à la différence entre l'extremum précédent et la tendance, en bref, l'amplitude était presque la même. Les données les plus récentes font exception, mais elles sont extrêmes. Fondamentalement, un tel indicateur devrait se redessiner si le nombre de points de données est faible ; cependant, s'ils sont augmentés, disons jusqu'à 2000, les problèmes de redessin ne se poseront pas.