Population optimization algorithms: Nelder–Mead, or simplex search (NM) method

Contents

1. Introduction
2. Algorithm
3. Test results

1. Introduction

The Nelder-Mead method was developed in 1965 by John Nelder and Roger Mead. They were looking for an optimization method that could work with functions that did not have derivatives or did not have analytical equations for derivatives. They also wanted to develop a method that would be easy to implement and efficient for use on the computing machines of the day. The research led them to the idea of using a simplex - a polyhedron in the space of function parameters.

The history of the method's creation began with the work of John Nelder and his colleagues at the Computing Laboratory in Oxford. They were faced with the problem of optimizing functions that did not have analytical derivatives or were too complex to calculate. Traditional optimization methods such as gradient methods were not applicable in such cases. Instead, Nelder and Mead proposed a new method based on iteratively searching for the optimal solution in the space of the function parameters.

The Nelder-Mead method was called the "simplex method" and was published in the article "A Simplex Method for Function Minimization" in The Computer Journal in 1965. This method has been accepted by the scientific community and has become widely used in various fields requiring function optimization.

A simplex is a set of points forming a polyhedron, where each point is a set of parameter values of the function being optimized. The idea is to change and move the simplex in the parameter space to find the optimal value of the function.

The Nelder-Mead method (Nelder-Mead simplex method) belongs to the class of unconditional optimization algorithms. It is a deterministic algorithm that does not require the use of function derivatives and can work with functions that have multiple local minimums.

2. Algorithm

The Nelder-Mead method is not a population method because only one optimization agent is used, representing a simplex, which in turn consists of a set of points in the search space, which itself can be considered a population. However, we will use several agents, each having its own simplex, so this implementation may well be classified as a population algorithm.

So, for ease of understanding, assume that it is necessary to optimize two variable functions. In other words, the dimension of the space is z = 2, then the simplex will consist of z + 1 = 3 vertices. Changing the simplex is an operation on the worst point of these three. Let's denote these points as Best, Good, Worst, with Good being the second point after Worst (if the dimension is greater than two, then Good will always be the second after Worst from the sorted list of vertices).

Next, we need to use these three vertices to calculate and adjust Worst relative to the remaining vertices. We move Worst relative to the geometric center of the vertices with the exception of itself, i.e. calculate the centroid and move Worst relative to the centroid.

At each iteration of the Nelder-Mead method, we perform the following steps:

1. Sorting the vertices of the simplex according to the values of the objective function, i.e. 

f(P0) ⩾ f(P1) ⩾ ... ⩾ f(P(n-1))

where:

• P0, P1 ... P(n-1) - simplex points
• n - number of simplex vertices
  

2. Centroid calculation: calculate the average value over the corresponding coordinates of all vertices of the simplex, except the worst vertex. Let the Xo vector will be the center of gravity of all vertices except X(n-1), then: 

Xo = (X0 + X1 + ... + X(n-2)) / (n-1)

where:

• X0, X1 ... X(n-2) - corresponding vectors of coordinates of all vertices except the worst one

3. Reflection: reflecting the worst vertex relative to the centroid. The Xr vector of the new reflected vertex is calculated the following way:

Xr = Xo + α (Xo - Xw)

where:

• Xw - worst vertex vector, corresponds to the vertex P(n-1)
  
• α - reflection ratio, usually equal to 1
  

4. Evaluation of a new vertex: the value of the objective function is calculated at this point. If a new vertex has an objective function value better than the worst vertex of the simplex, then it can replace it, i.e. the reflection replaces the original. The reflection operation allows us to explore a new region of the parameter space by reflecting from the simplex centroid.

5. Expansion: used to further explore the parameter space when a reflection operation has produced a vertex better than the best one, under the assumption that further movement in the reflection direction will further improve its position. The expansion operation allows us to explore an even larger region of the parameter space than the reflection operation. It increases the distance between the centroid and the reflected point, which can help find new local minimums of the objective function. The Xe expansion vector can be calculated as follows:

Xe = Xo + γ(Xr - Xo)

where:

• γ -  expansion ratio, usually greater than 1, the default is 2

5.1. If the expansion operation was performed: the fitness function for the Xe vertex is calculated. If it is better than the Xr vertex, then it can replace the worst Xw simplex vertex. After completing the expansion, move on to step 1.

Be sure to select the γ expansion ratio carefully. If it happens to be too large, it may cause the simplex to spread over a large region of the parameter space, which may slow down convergence or lead to loss of information about local extrema. If it turns out to be too small, it may not sufficiently explore new regions of the parameter space.

6. Contraction: used to calculate the Xc vertex when the reflection operation produced a vertex worse than or equal to the Xb good point (second after the worst), i.e. we attempt to find a better position within the simplex. The equation is as follows:

Xc = Xo + β(Xw - Xo)

where:

• β - contraction ratio, usually between 0 and 1, default 0.5

6.1. If a contraction was performed: the value of the Xc objective function for the vertex is calculated. If a new vertex has an objective function value better than the worst vertex of the simplex, then it can replace the worst. After completing the expansion, move on to step 1.

The contraction allows us to move the simplex closer to the worst point, which can help in exploring the vicinity of this point. As with the expansion, it is important to choose the β contraction ratio carefully. If it happens to be too large, it may cause the simplex to be compressed too much, resulting in a loss of information about local minimums. If it turns out to be too small, the compression may not be sufficient to explore the vicinity of the worst point.

7. Shrinkage: the last operation in the Nelder-Mead method is performed when none of the previous operations (reflection, expansion, contraction) leads to an improvement in the objective function value. Shrinkage reduces the size of the simplex to narrow the search area and focus around the sweet spot.

As we can see, the authors have four operations with the simplex. In order to start optimization, we need to calculate the fitness function for all simplex points. The number of simplex points is equal to "z+1", where z is the dimension of the search space. For example, if we have a search dimension of 1000, then we should evaluate the fitness function 1001 times to begin simplex operations. While a typical population algorithm with a population of 50 agents might run 20 epochs, this algorithm will only run one epoch and will consume most of its limited number of iterations.

Shrinkage involves shifting all points to the best one. After that, it is necessary to calculate the fitness function 1000 times. In other words, Shrinkage is very resource-intensive. According to the authors' idea, this operation should be called when the algorithm gets stuck and moving the worst point of the simplex does not improve the solution. However, my experiments showed that this operation is very expensive in relation to computing resources and, moreover, is meaningless and suicidal for the optimization algorithm, since the convergence of all points of the simplex agent to one local extremum would mean getting stuck and stopping the exploration of the search space. Therefore, I decided to abandon Shrinkage for the practical implementation of the algorithm.

We will use the first three operations with the simplex. They are displayed in Figure 1 for more clarity:

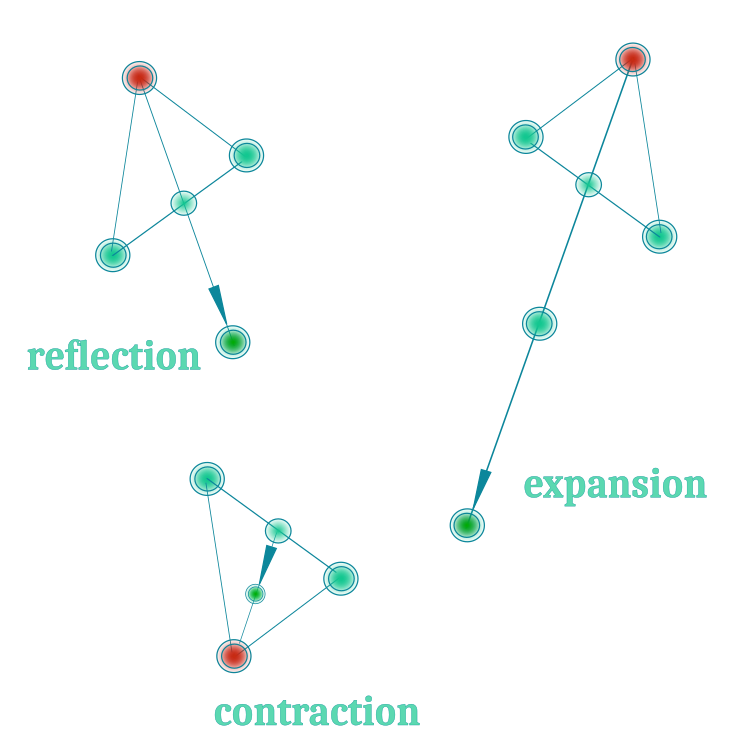
Figure 1. Three main operations of the Nelder-Mead method

Since the simplex search method may encounter poor selection of initial vertices since it is deterministic, its optimization result may be unsatisfactory. Experiments with this algorithm only confirmed fears: it works acceptably only in a limited coordinate space.

Due to convergence problems, the vertices of the simplex are simply shifted by a fixed value. Imagine standing on stilts and trying to sit on a bench. It is too low for you to do so. Exactly the same situation arises with a changing simplex. For the algorithm to work perfectly, we need to have a lot of luck so that the initial vertices of the simplex end up in the right place. This is similar to the stilts - in order to sit safely, we need a high bench. The algorithm converges relatively well on smooth monoextremal functions, for example, on a parabola. However, our practical problems are much more complex and are usually full of local "traps", especially in trading problems, which are discrete in nature.

Then the question arises. What to do when the simplex gets stuck "forever" at a local extremum? The logic of the Nelder-Mead algorithm does not provide ways to get out of this "trap". After each operation, be it contraction or expansion, the algorithm returns to reflection, trying to overcome the worst point. Visually this looks like "blinking". To solve this problem, I tried to give the simplex the ability to leave the local "trap" and continue searching in new areas of space. To achieve this, I used Levy's flights, which in some cases helped to "revive" the population, as described in previous articles. However, it is worth noting that Levy's Flights are not always useful and their application depends on the logic of the optimization algorithm. In our case, this was an experiment and improvement results were not guaranteed.

Now let's move on to the most interesting part - writing the code.

After each iteration, it is necessary to know which operation was performed on the worst vertex of the simplex. The enumerator will come in handy for this task. In addition to the three main operations with the vertex of a simplex, I added one more - "none", in case I decide to somehow supplement the algorithm. Let's call the enumerator E_SimplexOperation. It features the fields:

• none: no operations
• reflection
• expansion
• contraction
  

//——————————————————————————————————————————————————————————————————————————————
enum E_SimplexOperation
{
  none        = 0,
  reflection  = 1,
  expansion   = 2,
  contraction = 3
};
//——————————————————————————————————————————————————————————————————————————————

To describe the simplex vertex, we will need the S_Point structure, which contains the following fields:

• Init(int coords): point initialization, takes the "coords" argument
• c []: the array of coordinates of a point in multidimensional space, the size of the array is determined in the Init method
• f: vertex fitness function value
  

//——————————————————————————————————————————————————————————————————————————————
struct S_Point
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }
  double c [];
  double f;
};
//——————————————————————————————————————————————————————————————————————————————

For the simplex, we will use the S_Simplex structure, which is a simple simplex for each agent and contains the following fields:

• Init(int coords): simplex initialization, takes the "coords" argument - number of coordinates
• S_Point p []: array of simplex vertices, array size is determined in the Init method
• c []: the array of simplex centroid coordinates, the size of the array is determined in the Init method.
• S_Point Xr: reflection point
• S_Point Xe: expansion point
• S_Point Xc: contraction point
• indG: Good point index in the simplex
• indW: worst point index in the simplex
• E_SimplexOperation: simplex operation type

//——————————————————————————————————————————————————————————————————————————————
struct S_Simplex
{
  void Init (int coords)
  {
    ArrayResize (p, coords + 1);

    for (int i = 0; i <= coords; i++)
    {
      p [i].Init (coords);
    }

    ArrayResize (c, coords);

    Xr.Init (coords);
    Xe.Init (coords);
    Xc.Init (coords);

    operation = none;
  }

  S_Point p [];
  double c  []; //centroid

  S_Point Xr;  //reflection point
  S_Point Xe;  //expansion point
  S_Point Xc;  //expansion point

  int indG;    //index of good point
  int indW;    //index of worst point

  E_SimplexOperation operation; //type of simplex operation
};
//——————————————————————————————————————————————————————————————————————————————

Define the S_Agent structure for the optimization agent. The structure contains the following fields:

• Init (int coords): agent initialization method, takes the "coords" argument specifying the number of coordinates. The method resizes the array "c" to "coords" using the ArrayResize function. The "f" field is then set to -DBL_MAX, which is the initial value for the agent evaluation function. Next, the Init method is called for the "s" field, which represents the agent simplex
• c []: the array of agent coordinates in multidimensional space for exchange with an external program. The array size is determined in the Init method
• f: agent fitness function value
• s: agent simplex represented by the S_Simplex structure. The simplex is initialized by calling the Init method for the "s" field

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;

    s.Init (coords);
  }

  double c  []; //coordinates
  double f;     //fitness
  S_Simplex s;  //agent simplex
};
//——————————————————————————————————————————————————————————————————————————————

Define the simplex search method algorithm class C_AO_NMm, which contains the following fields:

• cB []: array of best coordinates
• fB: fitness function value of the best coordinates
• a []: the array of agents represented by the S_Agent structure
• rangeMax []: array of maximum search range values for each coordinate
• rangeMin []: array of minimum search range values for each coordinate
• rangeStep []: array of search steps for each coordinate
• Init (const int coordsP, const int popSizeP, const double reflectionCoeffP, const double expansionCoeffP, const double contractionCoeffP): algorithm initialization method, takes arguments defining the number of coordinates, population size, ratios for reflection, expansion, and compression operations, the method performs initialization of all class fields
• Moving (): the method performs the movement of agents in the algorithm
• Revision(): the method performs the movement of agents in the algorithm
• Sorting, CalcCentroid, Reflection, Expansion, Contraction, Flying: perform operations with simplexes. The 
• SeInDiSp, RNDfromCI and Scale methods are performed to generate and convert values into valid ranges with a given step
  

//——————————————————————————————————————————————————————————————————————————————
class C_AO_NMm
{
  //----------------------------------------------------------------------------
  public: double cB [];  //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Agent a [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //Reflection coefficient
                     const double expansionCoeffP,    //Expansion coefficient
                     const double contractionCoeffP); //Contraction coefficient

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;        //coordinates number
  private: int    popSize;       //population size
  private: int    simplexPoints; //simplex points


  private: double reflectionCoeff;  //Reflection coefficient
  private: double expansionCoeff;   //Expansion coefficient
  private: double contractionCoeff; //Contraction coefficient

  private: bool   revision;

  private: S_Point pTemp [];
  private: int     ind   [];
  private: double  val   [];

  private: void   Sorting      (S_Point &p []);
  private: void   CalcCentroid (S_Simplex &s, int indW);
  private: void   Reflection   (S_Agent &agent, int indW);
  private: void   Expansion    (S_Agent &agent);
  private: void   Contraction  (S_Agent &agent, int indW);
  private: void   Flying       (S_Agent &agent, int indW);

  private: double SeInDiSp     (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI    (double min, double max);
  private: double Scale        (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

To initialize the algorithm, use the Init method of the C_AO_NMm class, which initializes all fields of the class and creates the necessary arrays for the optimization algorithm to work.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //reflection coefficient
                     const double expansionCoeffP,    //expansion coefficient
                     const double contractionCoeffP)  //contraction coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords        = coordsP;
  popSize       = popSizeP;
  simplexPoints = coords + 1;

  reflectionCoeff  = reflectionCoeffP;
  expansionCoeff   = expansionCoeffP;
  contractionCoeff = contractionCoeffP;

  ArrayResize (pTemp, simplexPoints);
  ArrayResize (ind,   simplexPoints);
  ArrayResize (val,   simplexPoints);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++)
  {
    a [i].Init (coords);
  }

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Usually we use the Moving method to move agents in the search space, but for the NM algorithm we will leave only the function of the initial random placement of the vertices of agent simplexes in the search space.
To create a random vertex of simplexes, we use RNDfromCI and bring it to the required range with the required step using the SeInDiSp method.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Moving ()
{
  if (!revision)
  {
    int cnt = 0;

    for (int i = 0; i < popSize; i++)
    {
      for (int p = 0; p < simplexPoints; p++)
      {
        cnt++;
        for (int c = 0; c < coords; c++)
        {
          a [i].s.p [p].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
          a [i].s.p [p].c [c] = SeInDiSp  (a [i].s.p [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The main logic for moving the vertices of agents' simplexes will be carried out in the Revision method.

If the revision has not yet been performed "if (!revision)", then it is necessary to sort the vertices in the simplex, construct a centroid and perform reflection for the worst vertices of the agents' simplexes. This is the very first operation with vertices and it is always "reflection". Here we can update the global solution, since at this point we have knowledge of the fitness value for each vertex. Setting the value of the "revision" variable to 'true' and exiting the method.

Starting from the next iteration, we will know the fitness function not for the vertices of simplexes, but for specific optimization agents. In accordance with the performed operations on simplexes, we will assign known solutions of agents to their corresponding simplex vertices. We need to update the global solution with the best fitness values of the agents.

Next, check what operation was performed on the vertices at the previous iteration. We mean that the vertices of simplexes are vectors.

If "reflection" was performed:

• assign the agent fitness value to the Xr vector
• compare the Xr vector fitness with Xw. If the value is better, then update the Xw vector
• compare the Xr vector fitness with Xb. If the value is better, then perform the "expansion"
• compare the Xr vector fitness with Xg (second after the worst vertex), and if the value is worse, then perform "compression"
• if there was an improvement of the vertex, perform "reflection" with preliminary sorting and construction of the centroid. Otherwise, perform "Flying" 
  

If the "expansion" was performed:

• assign the agent fitness value to the Xe vector
• compare the Xe vector fitness with Xw. If the value is better, then update the Xw vector
  
• perform "reflection" with preliminary sorting and construction of the centroid
  

If the "contraction" was performed:

• assign the agent fitness value to the Xс vector
  
• compare the Xс vector fitness with Xw. If the value is better, then update the Xw vector. Otherwise, execute "Flying"
• if there was an improvement in the vertex, then perform "reflection" with preliminary sorting and construction of the centroid
  

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Revision ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    //sort agent simplex points by FF value and assign BGW
    for (int i = 0; i < popSize; i++)
    {
      Sorting (a [i].s.p);
    }

    //calculate the simplex centroid
    for (int i = 0; i < popSize; i++)
    {
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;

      CalcCentroid (a [i].s, a [i].s.indW);
    }

    //assign the next type of operation - reflection
    for (int i = 0; i < popSize; i++)
    {
      Reflection (a [i], a [i].s.indW);
      a [i].s.operation = reflection;
    }

    //save the best point of the agents’ simplexes as a global solution 
    for (int i = 0; i < popSize; i++)
    {
      if (a [i].s.p [0].f > fB)
      {
        fB = a [i].s.p [0].f;
        ArrayCopy (cB, a [i].s.p [0].c, 0, 0, WHOLE_ARRAY);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  if (revision)
  {
    int pos = -1;

    for (int i = 0; i < popSize; i++)
    {
      if (a [i].f > fB) pos = i;
    }

    if (pos != -1)
    {
      fB = a [pos].f;
      ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was reflection ++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == reflection)
    {
      a [i].s.Xr.f = a [i].f;
      bool needUpd = false;

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [a [i].s.indW].f)  //Xr > Xw                 |---w--Xr--g----------b---|
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xr;        //replace Xw with Xr
        needUpd = true;
      }
      
      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [0].f)             //if Xr > Xb            |---w----g----------b---Xr|
      {
        Expansion (a [i]);                            //perform expansion
        continue;
      }

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f <= a [i].s.p [a [i].s.indG].f) //if Xr < Xg            |---w---Xr--g----------b--|
      {
        Contraction (a [i], a [i].s.indG);            //perform contraction
        continue;
      }
      
      if (needUpd)
      {
        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was expansion +++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == expansion)
    {
      a [i].s.Xe.f = a [i].f;

      if (a [i].s.Xe.f > a [i].s.Xr.f) a [i].s.p [a [i].s.indW] = a [i].s.Xe;
      else                             a [i].s.p [a [i].s.indW] = a [i].s.Xr;

      Sorting (a [i].s.p);
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;
      CalcCentroid (a [i].s, a [i].s.indW);
      Reflection   (a [i],   a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was contraction +++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == contraction)
    {
      a [i].s.Xc.f = a [i].f;

      if (a [i].s.Xc.f > a [i].s.p [a [i].s.indW].f)
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xc;

        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

To calculate the centroid, we will write the CalcCentroid method. It calculates the average value of the coordinates in the given simplex "s" up to the specified indW index.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::CalcCentroid (S_Simplex &s, int indW)
{
  double summ = 0.0;

  for (int c = 0; c < coords; c++)
  {
    summ = 0.0;

    for (int p = 0; p < simplexPoints; p++)
    {
      if (p != indW) summ += s.p [p].c [c];
    }

    s.c [c] = summ / coords;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The "reflection" operation will be performed by the Reflection method for the indW index vertex of the "agent" simplex.

Inside the loop, calculate the reflected value Xr using the equation Xr = Xo + reflectionCoeff * (Xo - Xw). Here reflectionCoeff is a reflection ratio, which determines the degree of deviation of the reflected vertex from the initial vertex.
Next, apply the SeInDiSp to Xr to ensure that it is within the valid rangeMin[c] and rangeMax[c] range with the step of rangeStep[c]. The result is saved in agent.s.Xr.c[c].
Setting the "reflection" operation for the agent.s.operation agent indicating that the "reflection" operation has been performed for this agent.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Reflection (S_Agent &agent, int indW)
{
  double Xo;
  double Xr;
  double Xw;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c [c];
    Xw = agent.s.p [indW].c [c];

    //Xr = Xo + RNDfromCI (0.0, reflectionCoeff) * (Xo - Xw);
    Xr = Xo + reflectionCoeff * (Xo - Xw);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————

The "expansion" operation will be performed by the Expansion method for the "agent".

Inside the loop, calculate the expanded value of Xe using the equation Xe = Xo + expansionCoeff * (Xr - Xo). Here expansionCoeff is the expansion ratio that determines the degree of increase in the deviation of the expanded vertex from the initial vertex.
Next, apply the SeInDiSp to Xe to ensure that it is within the valid rangeMin[c] and rangeMax[c] range with the step of rangeStep[c]. The result is saved in agent.s.Xe.c[c].
Setting the "expansion" operation for the agent.s.operation agent indicating that the "expansion" operation has been performed for this agent.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Expansion (S_Agent &agent)
{
  double Xo;
  double Xr;
  double Xe;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xr = agent.s.Xr.c [c];

    //Xe = Xo + RNDfromCI (0.0, expansionCoeff) * (Xr - Xo);
    Xe = Xo + expansionCoeff * (Xr - Xo);

    agent.s.Xe.c [c] = SeInDiSp  (Xe, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xe.c [c];
  }

  agent.s.operation = expansion;
}
//——————————————————————————————————————————————————————————————————————————————

The "contraction" operation will be performed by the Contraction method for the indW index vertex of the "agent" simplex.

Inside the loop, calculate the compressed value of Xc using the equation Xc = Xo + contractionCoeff * (Xw - Xo) . Here contractionCoeff is the contraction ratio, which determines the degree the deviation of the compressed vertex from the initial vertex is reduced to.
Next, apply the SeInDiSp to Xc to ensure that it is within the valid rangeMin[c] and rangeMax[c] range with the step of rangeStep[c]. The result is saved in agent.s.Xc.c[c].
Setting the "contraction" operation for the agent.s.operation agent indicating that the "contraction" operation has been performed for this agent.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Contraction (S_Agent &agent, int indW)
{
  double Xo;
  double Xw;
  double Xc;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xw = agent.s.p [indW].c [c];

    //Xc = Xo + RNDfromCI (0.0, contractionCoeff) * (Xw - Xo);
    Xc = Xo + contractionCoeff * (Xw - Xo);

    agent.s.Xc.c [c] = SeInDiSp  (Xc, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xc.c [c];
  }

  agent.s.operation = contraction;
}
//——————————————————————————————————————————————————————————————————————————————

For Levy Flights, we apply the Flying method, which performs a "flying" operation for the "agent" with the goal of pushing the vertex of the simplex to new places in the search space with a random distribution that concentrates the probability closer to the best global solution with a decrease in probability down to 0 towards the boundaries of the studied space.

After applying the Flying method, set the "reflection" operation for agent.s.operation, so that in subsequent iterations the logic of the algorithm is executed as if the reflection operation had been performed.
Apply the SeInDiSp to Xr to ensure that it is within the valid rangeMin[c] and rangeMax[c] range with the step of rangeStep[c]. The result is saved in agent.s.Xr.c[c].

Thus, the Flying method performs a "flight" operation on the agent, changing its coordinates based on the current coordinates of the global best solution and randomly generated values. This allows the agent to explore new areas of solution space and potentially find more optimal solutions.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Flying (S_Agent &agent, int indW)
{
  for (int c = 0; c < coords; c++)
  {
    double r1 = RNDfromCI (-1.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);
    r2 = pow (r2, -2.0);

    if (r1 > 0.0) Xr = cB [c] + Scale (r2, 0.0, 1.0, 0.0, rangeMax [c] - cB [c], false);
    else          Xr = cB [c] - Scale (r2, 0.0, 1.0, 0.0, cB [c] - rangeMin [c], false);

    //Xr = RNDfromCI (rangeMin [c], rangeMax [c]);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————

3. Test results

NM test stand results:

C_AO_NMm:5;1.0;2.0;0.5
=============================
5 Rastrigin's; Func runs 10000 result: 77.96849465506082
Score: 0.96607
25 Rastrigin's; Func runs 10000 result: 61.68192953373487
Score: 0.76427
500 Rastrigin's; Func runs 10000 result: 50.62713783555849
Score: 0.62730
=============================
5 Forest's; Func runs 10000 result: 0.9552378700292385
Score: 0.54033
25 Forest's; Func runs 10000 result: 0.45877475613538293
Score: 0.25951
500 Forest's; Func runs 10000 result: 0.09902427974784639
Score: 0.05601
=============================
5 Megacity's; Func runs 10000 result: 5.6
Score: 0.46667
25 Megacity's; Func runs 10000 result: 2.304
Score: 0.19200
500 Megacity's; Func runs 10000 result: 0.40280000000000005
Score: 0.03357
=============================
All score: 3.90573

Based on the algorithm results, we can notice pretty decent results on the smooth Rastrigin function.

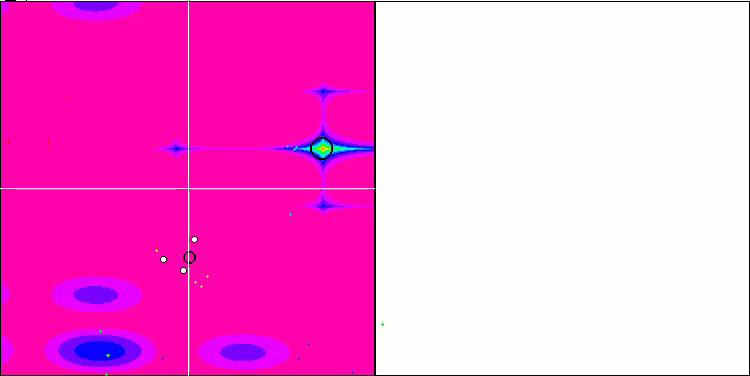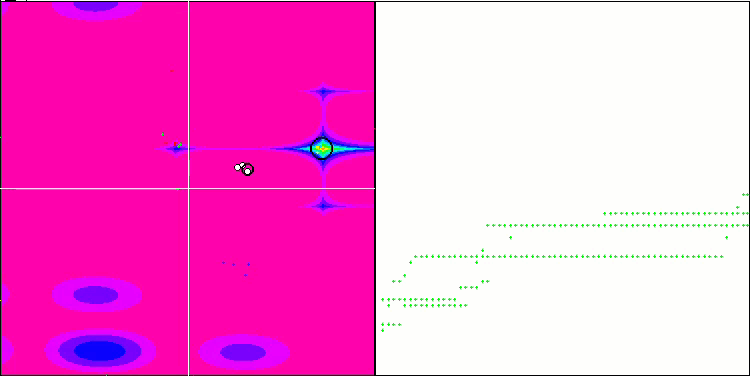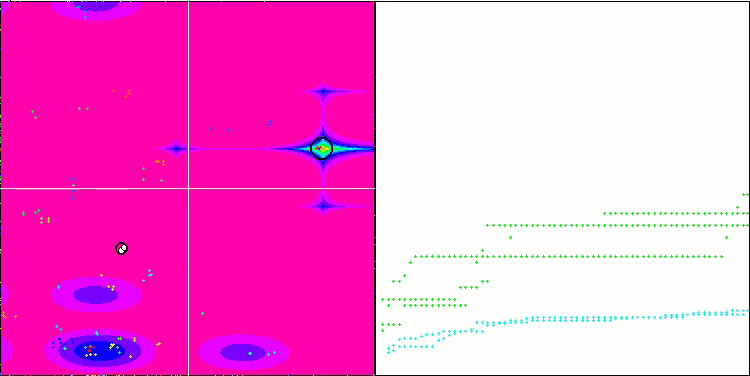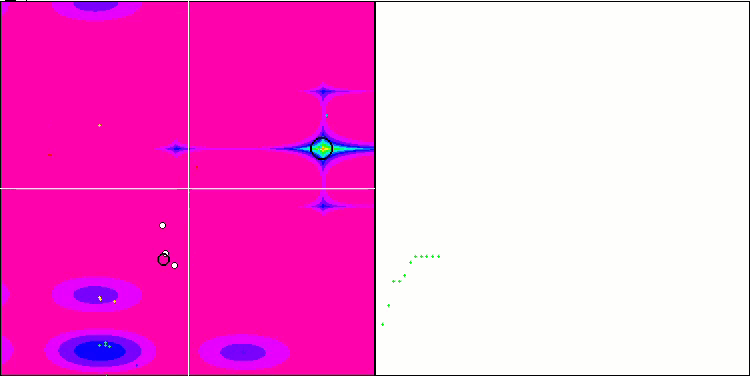
Visualization demonstrates signs of the population degeneration and concentration of agents in one place. The situation is somewhat improved by the use of Levy flights. This is noticeable at individual points of the corresponding coordinates. The convergence graphs are not very stable. I have only visualized the first two tests for each function because the third test with 1000 variables takes so long to run that it is not possible to show it in a GIF.

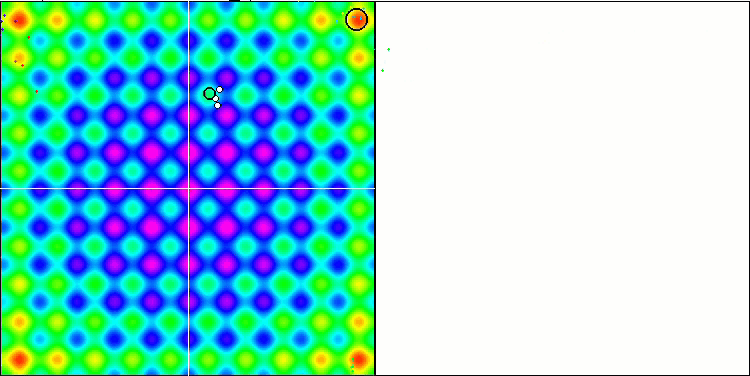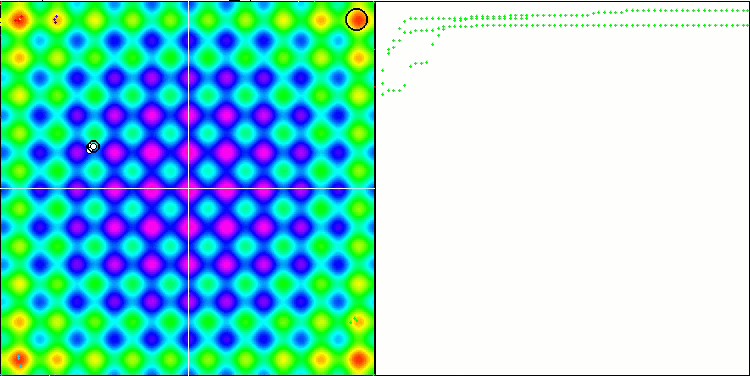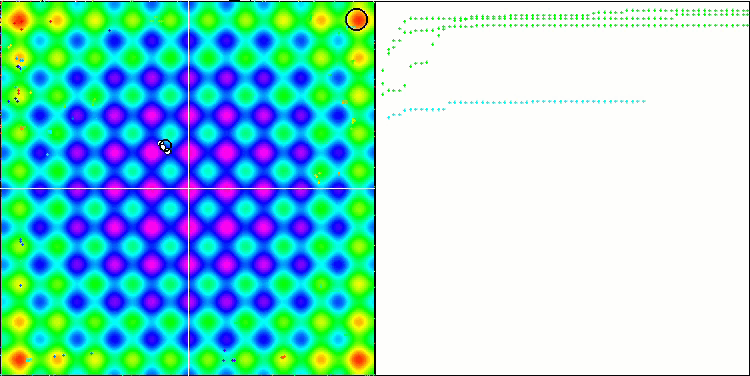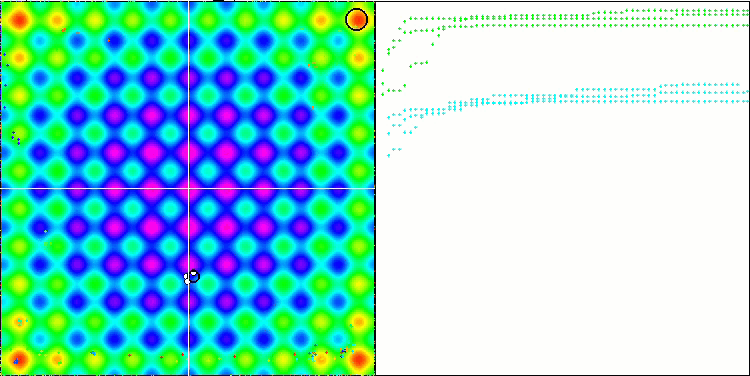
  NMm on the Rastrigin test function.

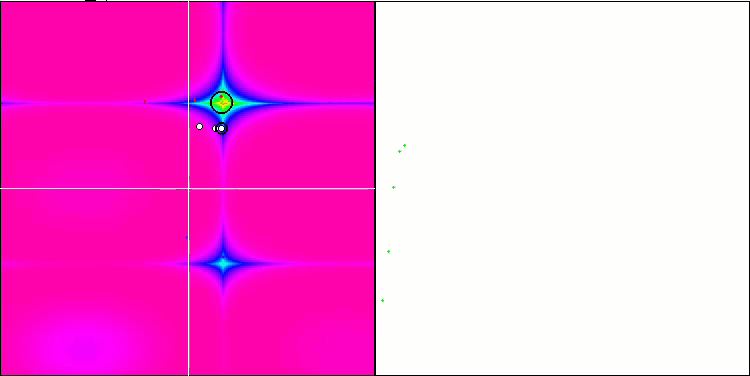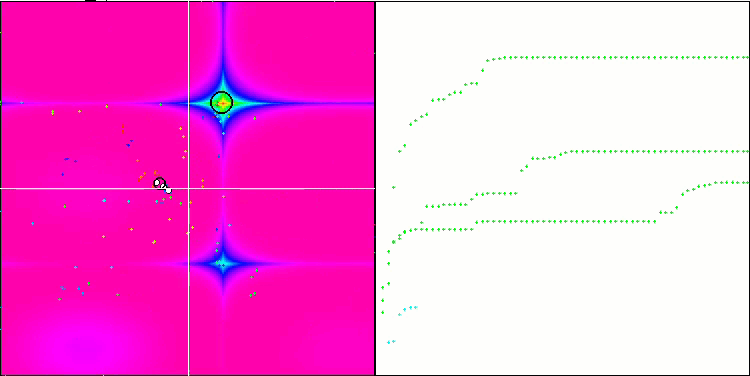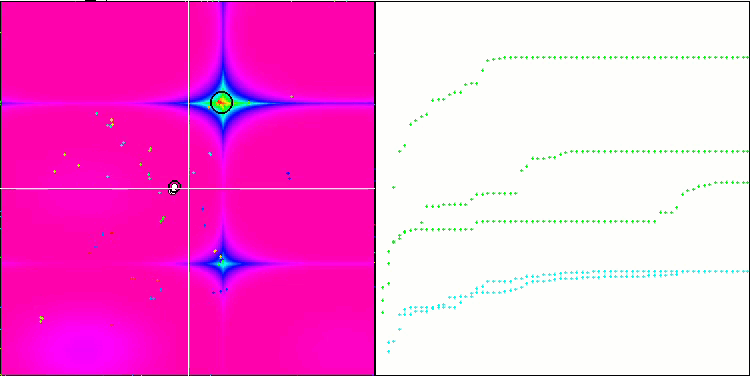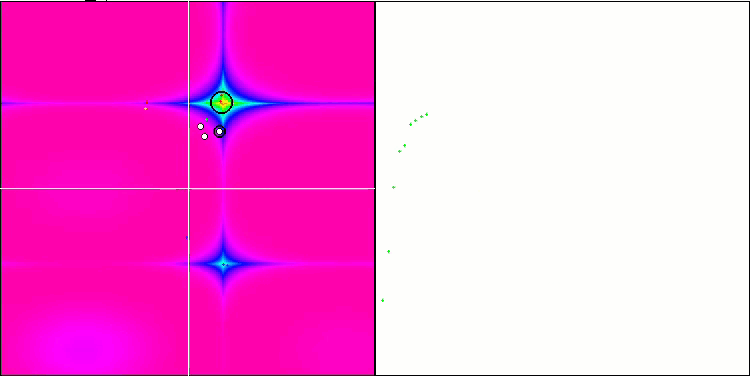
  NMm on the Forest test function.

  NMm on the Megacity test function.

Despite its many shortcomings, the Nelder-Mead method algorithm ended up in the 9th place.

#	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastic diffusion search M	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	1.00000	2.99265	1.00000	1.00000	1.00000	3.00000	100.000
2	SSG	saplings sowing and growing	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.83760	2.21081	0.54782	0.61841	0.99522	2.16146	77.683
3	DE	differential evolution	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.65510	2.50112	0.90000	0.52237	0.12031	1.54268	73.099
4	HS	harmony search	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.37529	2.04919	0.71739	0.71842	0.41338	1.84919	70.623
5	IWO	invasive weed optimization	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.26613	1.28755	0.57391	0.30527	0.33130	1.21048	48.250
6	ACOm	ant colony optimization M	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.64798	2.19925	0.71739	0.63947	0.05579	1.41265	47.387
7	MEC	mind evolutionary computation	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.21324	1.09615	0.66957	0.30000	0.26045	1.23002	44.049
8	SDOm	spiral dynamics optimization M	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.37600	1.36183	0.35653	0.15262	0.25842	0.76758	40.289
9	NMm	Nelder-Mead method M	0.88433	0.48306	0.45945	1.82685	0.46155	0.24379	0.21903	0.92437	0.46088	0.25658	0.16810	0.88555	39.660
10	COAm	cuckoo optimization algorithm M	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.13842	0.95200	0.52174	0.24079	0.17001	0.93254	37.830
11	FAm	firefly algorithm M	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.41704	1.21519	0.24783	0.20526	0.35090	0.80398	33.139
12	ABC	artificial bee colony	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.11177	0.79355	0.40435	0.19474	0.13859	0.73768	29.766
13	BA	bat algorithm	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.21769	0.54488	0.21305	0.07632	0.17288	0.46225	29.499
14	CSS	charged system search	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.13638	0.29452	0.07392	0.00000	0.03465	0.10856	27.930
15	GSA	gravitational search algorithm	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.27812	0.84322	0.42609	0.25525	0.00000	0.68134	27.807
16	BFO	bacterial foraging optimization	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.17298	0.75026	0.37392	0.24211	0.18841	0.80444	27.542
17	EM	electroMagnetism-like algorithm	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	19.002
18	SFL	shuffled frog-leaping	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.02221	0.25063	0.19565	0.04474	0.06607	0.30646	13.200
19	MA	monkey algorithm	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.07482	0.22852	0.15652	0.03553	0.10669	0.29874	11.777
20	FSS	fish school search	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.05458	0.21647	0.12175	0.03947	0.08244	0.24366	11.332
21	IWDm	intelligent water drops M	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.05112	0.38916	0.22609	0.05659	0.05054	0.33322	10.423
22	PSO	particle swarm optimisation	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.18207	0.44175	0.16956	0.04737	0.01947	0.23641	8.426
23	RND	random	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03949	0.20648	0.12175	0.03290	0.04898	0.20363	5.054
24	GWO	grey wolf optimizer	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02545	0.31812	1.000

Summary

The Nelder-Mead algorithm is of little use in modern heavy optimization problems, since it requires calculating the fitness function for each vertex of the simplex at the initial stage, which negates its ability to be used for multidimensional search spaces, so the algorithm cannot be recommended for use, despite its relatively good results and place in the rating table.

The SDS algorithm was removed from the table and only its modified version was left.

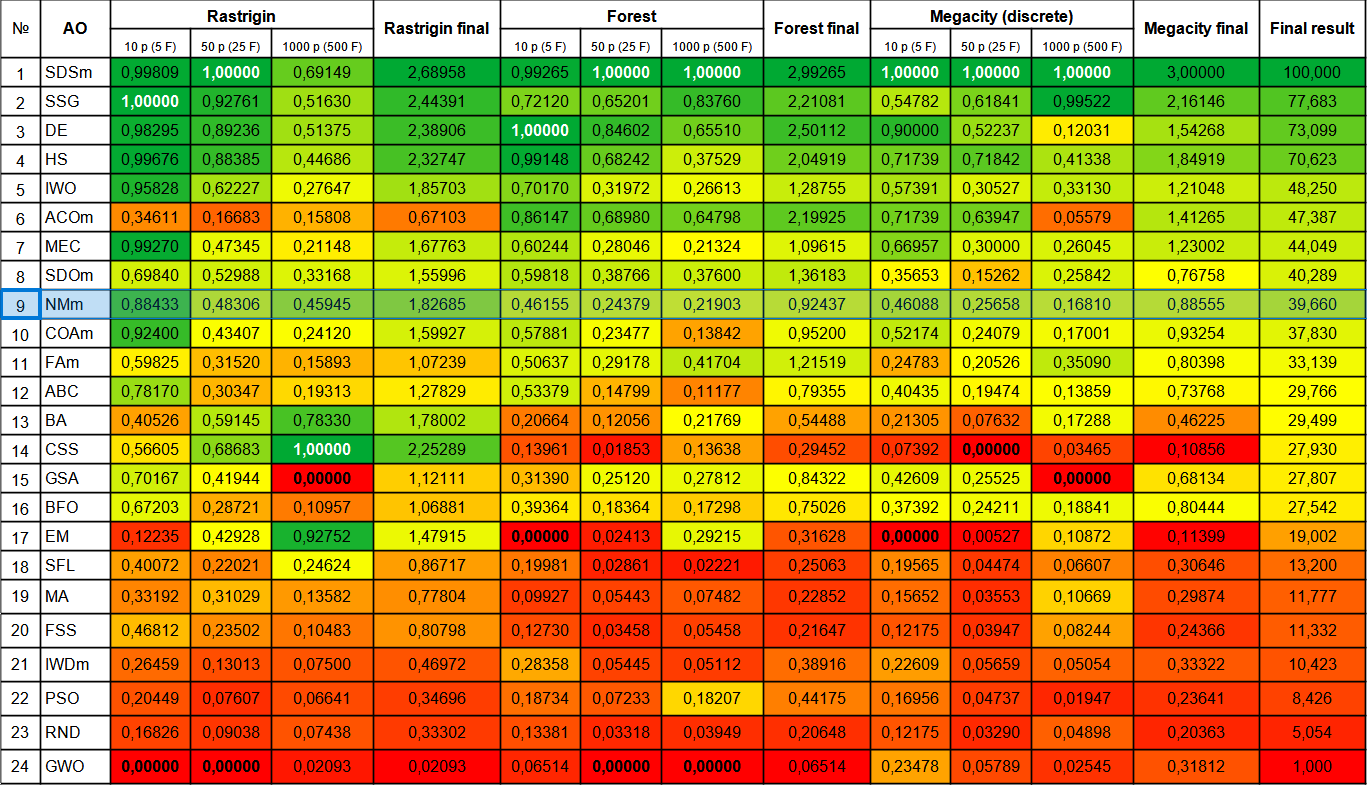
Figure 2. Color gradation of algorithms according to relevant tests

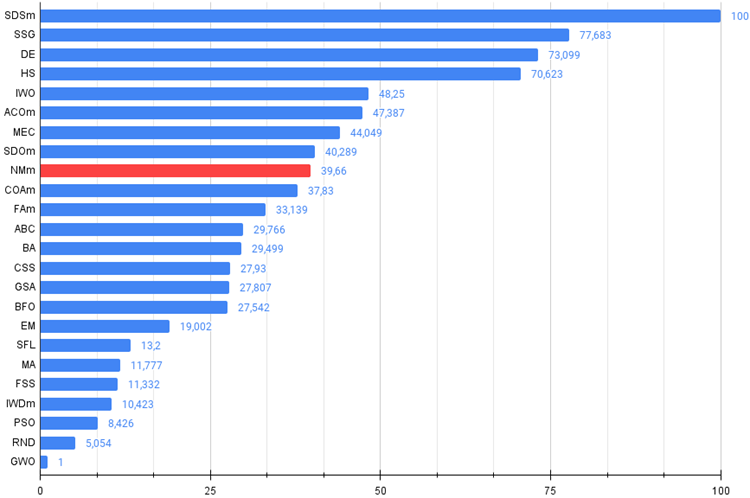
Figure 3. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

the archive contains the script for calculating the rating table using the method applied in the article).

Pros and cons of the modified Nelder-Mead (NMm) algorithm:

Advantages:

1. A small number of external parameters.
2. Good results on smooth functions with small number of variables.
   

Disadvantages:

1. Complex implementation.
2. Difficult to use with third-party applications due to the need to pre-calculate fitness for all simplex vertices.
3. Low operation speed.
4. Very poor scalability.
5. High scatter of results.
6. Tendency to get stuck in local extremes.

Please note that the Pros and Cons relate specifically to the modified version of the simplex search. There is no point in including the regular NM version in the table because of the very weak results.

The article is accompanied by an archive with updated current versions of the algorithm codes described in previous articles. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.