Методы прогнозирования временных рядов
1. Прогнозирование как задача анализа временного ряда. Детерминированная и случайная составляющие: способы их выделения и оценки.
Прогнозирование – это научное выявление вероятностных путей и результатов предстоящего развития явлений и процессов, оценка показателей процессов для более или менее отдаленного будущего.
Изменение состояния наблюдаемого явления (процесса) характеризуется совокупностью параметров x1, x2, … , xt,…, измеренных в последовательные моменты времени. Такая последовательность называется временным рядом.
Анализ временных рядов – одно из направлений науки прогнозирования.
Если одновременно рассматриваются несколько характеристик процесса, то в этом случае говорят о многомерных временных рядах.
Под детерминированной (закономерной) составляющей временного ряда x1, x2, … , xn понимается числовая последовательность d1, d2, … , dn, элементы которой вычисляются по определенному правилу как функция времени t.
Если исключить из ряда детерминированную составляющую, то оставшаяся часть будет выглядеть хаотично. Ее называют случайной компонентой ε1, ε2, … , εn.
Модели разложения временного ряда на детерминированную и случайную компоненты:
1. Аддитивная модель:
xt = dt + εt, t=1,…n
2. Мультипликативная модель:
xt = dt · εt, t=1,…n
Если мультипликативную модель прологарифмировать, то получим аддитивную модель для логарифмов xt.
В детерминированной компоненте выделяют:
1) Тренд (trt) – плавно изменяющаяся нециклическая компонента, описывающая чистое влияние долговременных факторов, эффект которых сказывается постепенно.
2) Сезонная компонента (St) – отражает повторяемость процессов во времени.
3) Циклическая компонента (Ct) – описывает длительные периоды относительного подъема и спада.
4) Интервенция – существенное кратковременное воздействие на временной ряд.
Тренд
Модели тренда:
– линейная: trt = b0 + b1t
– нелинейные модели:
полиномиальная: trt = b0 + b1t + b2t2 + … + bntn
логарифмическая: trt = b0 + b1 ln(t)
логистическая: ![]()
экспоненциальная: trt = b0 · b1t
параболическая: trt = b0 + b1t + b2t2
гиперболическая: trt = b0 + b1 /t
и другие
Тренд используется для долгосрочного прогноза.
Выделение тренда:
1) Метод наименьших квадратов (время – фактор, временной ряд – зависимая переменная):
xti = f (ti, θ)+εt i=1,…n
f – функция тренда;
θ – неизвестные параметры модели временного ряда.
εt – независимые и одинаково распределенные случайные величины.
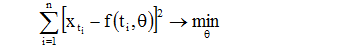
Если минимизировать функцию, можно найти параметры θ.
2) Применение разностных операторов
![]()
Разностный оператор второго порядка:
![]()
Выделение сезонных эффектов
Пусть m – число периодов, p – величина периода.
St = St+p, для любых t.
1) Оценка сезонной компоненты
а) Сезонные эффекты на фоне тренда
Для аддитивной модели xt = trt + St + εt оценка:
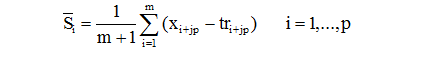
Если необходимо, чтобы сумма сезонных эффектов равнялась 0, то переходят к скорректированным оценкам сезонных эффектов:
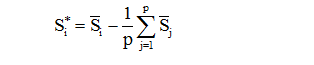
Для мультипликативной модели xt = trt * St * εt:
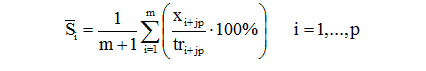
б) При наличии в ряде циклической компоненты (метод скользящих средних)
Идея метода: каждое значение исходного ВР заменяется средним значением на интервале времени, длина которого выбирается заранее. Выбранный интервал как бы скользит вдоль ряда.
Скользящее среднее ![]() при медианном сглаживании:
при медианном сглаживании: ![]() t=med (xt-m,xt-m+1, …,xt+m)
t=med (xt-m,xt-m+1, …,xt+m)
При средне арифметическом сглаживании:
xt=1/(2m+1)(xt-m+xt-m+1+…+xt+m), если р – четный,
xt=1/(2m)(1/2*xt-m+xt-m+1+…+1/2*xt+m) если р – нечетный.
Для аддитивной модели xt = trt +Ct + St + εt.
Для упрощения обозначений: начнем нумерацию величин![]() с единицы, изменим
нумерацию исходного ряда так, чтобы величине x соответствовал член xt.
с единицы, изменим
нумерацию исходного ряда так, чтобы величине x соответствовал член xt.
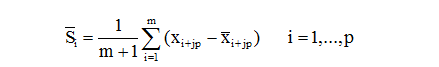
![]() – скользящее среднее с
периодом p, построенное по xt.
– скользящее среднее с
периодом p, построенное по xt.
Для мультипликативной модели – перейти к логарифмам и получить мультипликативную модель.
xt = trt · Ct · St · εt
yt = log xt, dt = log trt, gt = log Ct, rt = log St, δt = log εt
yt = dt + gt + rt + δt
2) Удаление сезонной компоненты (сезонное выравнивание)
а) При наличии оценок сезонной компоненты:
Для аддитивной модели – путем вычитания из начальных
значений ряда полученных сезонных оценок ![]() .
.
Для мультипликативной модели – путем деления начальных
значений ряда на соответствующие сезонные оценки ![]() и умножением на 100%.
и умножением на 100%.
б) Применение разностных операторов
![]()
где В – оператор сдвига назад.
Разностный оператор второго порядка:
![]()
Если ВР одновременно содержит тренд и сезонную компоненту, то их удаление возможно с помощью последовательного применения простых и сезонных разностных операторов. Порядок их применения не существенен:
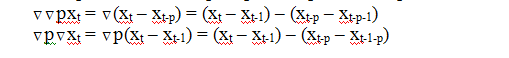
3) Прогнозирование с помощью сезонной компоненты:
Для аддитивной модели:
![]()
Для мультипликативной модели:
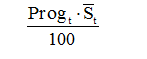
2. Модели временного ряда: AR(p), MA(q), ARIMA(p,d,q). Идентификация моделей, оценка параметров, исследование адекватности модели, прогнозирование.
Для описания вероятностной компоненты временного ряда используют понятие случайного процесса.
Случайным
процессом x(t), заданным на
множестве Т, называют функцию от t, значения
которой при каждом t ![]() T являются случайной величиной.
T являются случайной величиной.
Случайные процессы, у которых вероятностные свойства не изменяются во времени, называются стационарными (матожидание и дисперсия – константы).
В качестве модели стационарных временных рядов чаще всего используются:
- процессы авторегрессии;
- скользящее среднее;
- их комбинации.
Для проверки стационарности ряда остатков и оценки его дисперсии используют:
- выборочную автокорреляционную функцию (коррелограмму);
- частную автокорреляционную функцию.
Пусть εt – процесс белого шума, т.е. в разные моменты времени t случайные величины εt независимы и одинаково распределены с параметрами M(εt)=0, D(εt)=σ2=const. Тогда:
Случайный процесс x(t) со средним значением μ называется процессом авторегрессии порядка p (AR(p)), если для него выполняется соотношение:
x(t)-μ= α1 (x(t-1) – μ) + α2 (x(t-2) – μ) +…+ αp (x(t-p) – μ) + εt
Случайный процесс x(t) называется процессом скользящего среднего порядка q (MA(q)), если для него выполняется соотношение:
x(t)= εt + β1 εt-1 +…+ βq εt-q
Случайный процесс x(t) называется процессом авторегрессии-скользящего среднего порядков p и q (ARMA(p,q)), если для него выполняется соотношение:
![]()
Нестационарные технические и экономические процессы могут быть описаны модифицированной моделью ARMA(p,q). Для удаления тренда можно использовать разностные операторы.
Пусть даны две последовательности U=(…,U-1,U0,U1,…) и V=(…,V-1, V0,V1,V2,…) такие, что:
![]() означает
означает ![]() ,для
,для ![]()
![]() означает
означает ![]() и т.д.
и т.д.
Тогда процесс AR(p)
представляется в виде ![]() ,
,
MA(q): ![]() ,
,
ARMA(p,q): ![]()
B можно использовать как разностный оператор, т.е. ![]()
эквивалентно V=(1-B)U
Для разностей второго порядка:
z =(1-B)V=(1-B)2U
Таким образом получим модель авторегрессии-проинтегрированного скользящего среднего порядков p, d и q (ARIMA(p,d,q)), определяемую уравнениями:
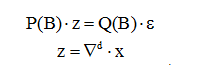
где ![]() – разностный оператор
порядка d;
– разностный оператор
порядка d; ![]() x=(1-B)dx.
x=(1-B)dx.
Идентифицировать модель – определить ее параметры p, d и q. Для идентификации модели служат графики частных автокорреляционных (АКФ) и частных автокорреляционных функций (ЧАКФ).
АКФ. k-й член АКФ определяется по формуле:
 (*)
(*)
Параметр k называют лагом. На практике k < n/4. График АКФ – коррелограмма. Если полученный ряд остатков нестационарный, то по коррелограмма можно определить причины нестационарности.
Значения
ЧАКФ akk находят, решая
систему Юла – Уолкера, используя значения АКФ ![]()
Система Юла – Уолкера:
![]()
r1 = a1 +
a2*r1 + … + ap*rp-1
r2 = a1*r1 + a2 + … + ap*rp-2
………………………………..
rp = a1*rp-1 + a2*rp-2 + …+ ap
После визуализации ряда и удаления тренда рассматривается АКФ. Если график АКФ не имеет тенденции к затуханию, то это нестационарный процесс (модель ARIMA). При наличии сезонных колебаний коррелограмма содержит периодические всплески, как правило, соответствующие периоду колебаний. Рассматриваются разности 1-го, 2-го,…k-го порядка, пока ряд не станет стационарным, тогда параметр d=k (обычно k не больше 2). Переходят к идентификации стационарной модели.
Идентификация стационарных моделей:
1) AR(p):
АКФ плавно спадает;
ЧАКФ обрывается на лаге p.
2) MA(q):
АКФ обрывается на лаге q.
ЧАКФ плавно спадает.
Оценка параметров m, ai модели AR(p):
В качестве оценки m можно взять среднее значении ВР
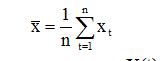
Для оценки ai найдем корреляцию между X(t) и X(t-k):
![]() (**)
(**)
Общее
решение этого уравнения относительно rk определяется
корнями характеристического уравнения ![]()
Пусть корни характеристического уравнения различны. Тогда общее решение может быть записано в виде:
![]()
Из требования стационарности следует, что все |λi|<1.
Если записать уравнение (**) для k=1, 2, 3…., получим систему Юла-Уоркера для AR(p) процесса:
r1 = a1 +a2*r1 + … + ap*rp-1
r2 = a1*r1 + a2 + … + ap*rp-2
………………………………..
rp = a1*rp-1 + a2*rp-2 + …+ap
Решая эту систему относительно a1, a2....ap, получим параметры AR(p).
Оценка параметра βi модели MA(q):
Для процесса МА(q) при |k| > q Cov[X(t), X(t+k)] = 0.
Cov[X(t), X(t+k)] = s2*(bk + b1*bk+1 + b2*bk+2 + … + bq-k*bq)
Отсюда автокорреляционная функция имеет вид:
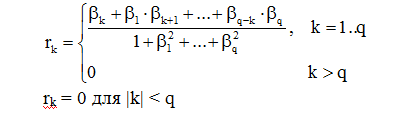 (***)
(***)
Для оценивания коэффициентов bi по наблюденному участку траектории существует несколько путей. Наиболее простой:
Находят
коэффициенты корреляции ![]() по формуле (*). Из
системы (***) получают систему нелинейных уравнений для нахождения bi. Она решается
итерационными методами.
по формуле (*). Из
системы (***) получают систему нелинейных уравнений для нахождения bi. Она решается
итерационными методами.
Прогнозирование. При прогнозировании необходимо получить детерминированные значения ВР по уже имеющимся формулам, а затем рассчитать случайные значения по подобранной модели и скорректировать детерминированные значения на величину случайных значений.
3. Прогнозирование с помощью искусственных нейронных сетей, метод окон.
Решение математических задач с помощью нейронных сетей (НС) осуществляется путем обучение НС способам решения этих задач.
Обучение многослойной нейронной сети производится методом обратного распространения ошибки (Back Propagation).
Модель искусственного нейрона
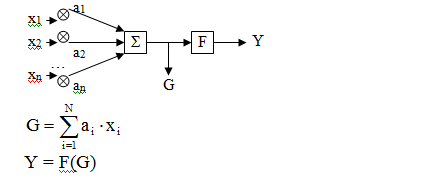
где xi – входные сигналы,
ai – коэффициенты проводимости (const), которые корректируются в процессе обучения,
F – функция активации, она нелинейная, в разных моделях может называться по-разному. Например, «сигмоида»:
Общая структура нейронной сети:
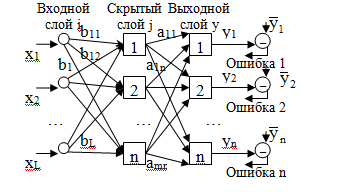
Скрытых слоев может быть несколько, поэтому НС – многослойная.
– вектор эталонных сигналов (желаемых)
yi – вектор реальных (выходных) сигналов
xi – вектор входных сигналов.
Стратегия обучения «обучение с учителем»
Типовые шаги: ![]()
1) Выбрать очередную обучающую пару 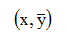 из обучающего
множества
из обучающего
множества ![]() .
.
x – входной вектор;
![]() – соответствующий ему
желаемый (выходной вектор).
– соответствующий ему
желаемый (выходной вектор).
Подать входной вектор х на вход НС.
2) Вычислить выход сети у – реальный выходной сигнал.
Предварительно, весовые коэффициенты aij и bij задаются произвольно случайным образом.
3) Вычислить отклонение (ошибку): ![]()
4) Подкорректировать веса aij и bij сети так, чтобы минимизировать ошибку.
![]()
5) Повторить шаги 1– 4.
Процесс повторяется до тех пор, пока ошибка на всем обучающем множестве не уменьшится до требуемой величины.
Проход вперед сигнала X по сети:
Из обучающего множества берется пара . Для каждого слоя, начиная с первого, вычисляется Y: Y = F(X·A),
где A – матрица весов слоя;
F – функция активации.
Вычисления – слой за слоем.
Обратный проход ошибки по НС:
Выполняется подстройка весов выходного слоя. Для этого применяется модифицируемое дельта-правило.

Рис. Обучение одного веса от нейрона p в скрытом слое j к нейрону q в выходном слое k
Для выходного нейрона сначала находится сигнал ошибки
![]()
εq умножается на производную сжимающей функции [y (1–y)], вычисленную для этого нейрона слоя k. Получаем величину δ:
δq= yqk · (1 – yqk) · εq
Далее как в обычном дельта-правиле находим:
Δapqk = α · δqk · ypj,
где α – коэффициент скорости обучения (0.01≤ α <1) – const, подбирается экспериментально в процесса обучения.
ypj – выходной сигнал нейрона p слоя j.
 – величина веса в
связке нейронов p→q на шаге t (до
коррекции) и шаге t+1 (после коррекции).
– величина веса в
связке нейронов p→q на шаге t (до
коррекции) и шаге t+1 (после коррекции).
Подстройка весов скрытого слоя.
Рассмотрим нейрон скрытого слоя p. При переходе вперед этот нейрон передает свой выходной сигнал нейронам выходного слоя через соединяющие их веса. Во время обучения эти веса функционируют в обратном порядке, пропуская величину δ от выхода назад к скрытому слою.
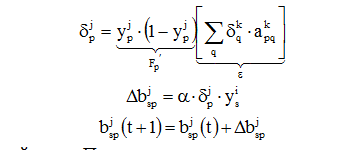
И так для каждой пары. Процесс заканчивается, если для
каждого X НС будет вырабатывать ![]()
Прогнозирование с помощью НС. Метод окон.
Задан временной ряд xt, t=1,2…T. Задача прогнозирования сводится к задаче распознавания образов на НС.
Метод выявления закономерности во временном ряде на основе НС называется “windowing” (метод окон).
Используется два окна Wi (input ) и Wo (output) фиксированного размера n и m соответственно, для наблюдаемого множества данных.
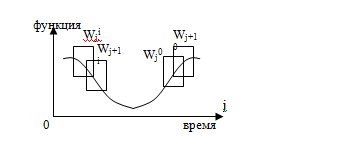
Эти окна способны перемещаться с некоторым шагом S по кривой (ряду) вдоль оси времени. В результате получается некоторая последовательность наблюдений:

Первое окно Wi, сканирует данные, предает их на вход НС, а Wo – на выход. Получающаяся на каждом шаге пара Wji→Wj0, j=1..n образует обучающую пару (наблюдение). После обучения НС можно использовать для прогноза.