MetaTrader 5 / 지표
English Русский 中文 Español Deutsch 日本語 Português Français Italiano Türkçe
지수 평활법을 이용한 시계열 예측(계속)

지수 평활법을 이용한 시계열 예측(계속)

MetaTrader 5 — 지표 | 5 8월 2021, 09:40
136 0
Victor
Victor

개요

'지수 평활법을 이용한 시계열 예측' 파트 1에서는 지수 평활화 모델에 대한 간략한 설명으로 시작해 모델 매개 변수 최적화 방법, 그리고 감쇠를 이용한 점진적 성장 모델을 기반으로 한 예측 인디케이터에 대해 다루었습니다. 파트 2는 파트 1 예측 인디케이터의 정확도 향상에 대한 내용입니다.

통화쌍 가격 또는 아무리 가까운 미래에 대한 것일지라도 신뢰할 만한 예측을 한다는 건 복잡한 일입니다. 따라서 먼 미래에 대한 예측은 거의 불가능하겠지만 그래도 12단계 예측 시스템 제작을 한번 시도해 볼까 합니다. 아무래도 신뢰 구간이 가장 좁게 나타나는 첫 몇 단계에 신중을 기울여야겠죠.

10~12단계 예측 시스템은 다양한 예측 메소드 및 모델의 행동 패턴에 대한 설명을 주요 목표로 합니다. 필요한 경우 모든 시간 간격에 대한 예측의 정확도는 신뢰 구간 오차 한계를 이용해 평가 가능합니다. 본문에서는 파트 1에서 만든 인디케이터의 기능을 향상시켜 줄 몇 가지 방법에 대해 알아 보겠습니다.

인디케이터 개발 단계에 필요한 최소 함수 설정을 위한 알고리즘은 지난 글에서 이미 다루었으므로 이번 글에서는 다루지 않습니다. 간단한 설명을 위해 이론에 관한 설명 또한 최소화하고자 합니다.

 

1. 기존 인디케이터

IndicatorES.mq5 인디케이터(이전 글 참조)를 이용하겠습니다.

해당 인디케이터를 컴파일하려면 동일한 디렉토리에 위치한 세 가지 파일, IndicatorES.mq5, CIndicatorES.mqh와 PowellsMethod.mqh가 필요한데요. 본문 하단에 위치한 files2.zip에도 포함되어 있습니다.

우선 기존 인디케이터 제작에 이용되었던 지수 평활화 모델 수식을 다시 살펴보겠습니다.

수식을 읽는 방법은 다음과 같습니다.

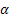  • -[0,1] 시퀀스 레벨 평활화 매개 변수
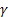  • -[0,1] 평활화 매개 변수
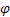  •  -[0,1] 감쇠 매개 변수
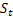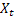  • -관측 후 주어진 시간 t의 시퀀스 레벨 평활화 값
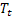  • -주어진 시간 t의 평활화 덧셈 추세
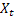  • -주어진 시간 t의 시퀀스 값
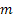  • -예측 단계 수
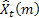  • -주어진 시간 t에서의 m단계 예측
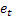  • -주어진 시간 t에서의 1단계 예측 오류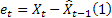

인디케이터의 유일한 입력 변수는 구간의 길이를 정의하는 값입니다. 이에 따라 초기 구간 값이 정해지고 모델의 매개 변수들이 최적화되죠. 주어진 구간 내 모델 매개 변수의 최적 값과 필요한 연산을 결정하면 1단계 예측 모델에 대한 예측 값, 신뢰 구간 및 차트 선이 나타납니다. 새로운 바가 생성될 때마다 매개 변수가 최적화되며 예측이 일어나고요.

해당 인디케이터의 업그레이드에 따른 결과 변화는 본문 하단에 첨부된 Files2.zip 파일에 첨부된 테스트 시퀀스를 이용해 평가하겠습니다. 첨부 파일의 \Dataset2 폴더에 EURUSD, USDCHF 및 USDJYP 통화쌍 시세 파일이 포함되어 있습니다. 미국 달러 지수(DXY) 파일 또한 찾아볼 수 있는데요. 각 파일은 M1, H1 그리고 D1의 세 가지 타임 프레임을 갖고 있습니다. 가장 최근 값이 파일의 제일 끝에 위치하도록 순서가 설정되어 있고요. 각 파일은 1200개의 엘리먼트를 포함합니다.

예측 오류는 평균절대비오차(MAPE) 계수를 이용해 측정됩니다.

총 12개의 테스트 시퀀스를 각각 80개의 엘리먼트를 포함하는 50개의 오버랩 구간으로 나누어 MAPE 값을 계산합니다. 이렇게 얻어진 추산치의 평균이 비교 대상 인디케이터에 대한 예측 오류 인덱스로 이용됩니다. 같은 방법으로 2단계 및 3단계 예측 오류 값을 계산합니다. 평균 추산치는 다음과 같이 표기합니다.

  • MAPE1–1단계 예측 오류 평균 추산치
  • MAPE2–2단계 예측 오류 평균 추산치
  • MAPE3–3단계 예측 오류 평균 추산치
  • MAPE1-3–평균값(MAPE1+MAPE2+MAPE3)/3

MAPE 값 계산 시 매 단계별로 예측 오류 절대값이 현재 시퀀스 값으로 나뉘어집니다. 0으로 나누거나 음수 값이 나오는 것을 방지하기 위해 인풋 시퀀스는 0이 아닌 양의 값을 취해야 하기 때문입니다.

표 1에 기존 인디케이터 예측 값이 나타나 있습니다.


 MAPE1
 MAPE2
 MAPE3
 MAPE1-3
IndicatorES
 0.2099
 0.2925
 0.3564
 0.2863


표 1. 초기 인디케이터 예측 오류 추산

표 1에 나타난 데이터는 Errors_IndicatorES.mq5 파일 스크립트(본문 하단 files2.zip에 포함)를 이용해 얻은 것입니다. 컴파일 및 스크립트 실행을 위해서는 CIndictorES.mqh 파일과 PowellsMethod.mqh 파일이 Errors_IndicatorES.mq5 파일과 동일한 디렉토리에 위치해야 하며 인풋 시퀀스는 Files/Dataset2/ 폴더에 저장되어야 합니다.

예측 오류 초기 추산치가 획득되었으니 본격적인 인디케이터 업그레이드를 시작하겠습니다.


2. 최적화 기준

'지수 평활법을 이용한 시계열 예측'에서 기존 인디케이터 모델 매개 변수는 1단계 예측 오류 값 제곱의 합의 최소화를 통해 결정되었습니다. 1단계 예측 모델에 최적화된 매개 변수가 2단계 이상 예측 모델에 대한 최소 오류값을 발생시키지 않는다고 봐도 되겠죠. 물론 10~12단계 예측 모델의 오류가 거의 없으면 좋겠지만 해당 시퀀스에 대해 만족스러운 예측 결과를 얻는 것은 거의 불가능한 일입니다..

따라서 매개 변수 최적화 시 1~3단계 예측 모델 오류 추산치의 제곱의 합을 이용하기로 합니다. 기존 인디케이터에 대한 첫 번째 업그레이드네요. 평균 오류 발생 횟수는 3단계에 걸쳐 점차 감소할 것으로 예측할 수 있습니다.

물론 기존 인디케이터의 주요 구조는 바꾸지 않고 매개 변수 최적화 기준만 변경하는 것입니다. 따라서 전체 예측 정확도가 갑자기 몇 배나 증가하기를 기대할 수는 없죠.

예측 결과를 비교하기 위해 지난 글에서 소개된 CIndicatorES 클래스와 유사한 CMod1 클래스를 생성합니다. 목적 함수 func가 수정되었죠.

기존 CIndicatorES 클래스의 func 함수는 다음과 같습니다.

double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}       // Alpha  > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}       // Alpha  < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}      // Gamma  > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}       // Gamma  < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }      // Phi    > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}       // Phi    < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }

약간의 수정을 거쳐 다음의 func 함수로 변경되었습니다.

double CMod1::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,err,ae,pt,phi2,phi3,a;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;        // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}       // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}      // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}       // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }      // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}       // Phi     < 0.05
  phi2=phi+phi*phi; phi3=phi2+phi*phi*phi;
  err=0;
  for(i=0;i<Dlen-2;i++)
    {
    e=Dat[i]-(s+phi*t); err+=e*e;
    a=Dat[i+1]-(s+phi2*t); err+=a*a;
    a=Dat[i+2]-(s+phi3*t); err+=a*a;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  e=Dat[Dlen-2]-(s+phi*t); err+=e*e;
  a=Dat[Dlen-1]-(s+phi2*t); err+=a*a;
  ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
  a=Dat[Dlen-1]-(s+phi*t); err+=a*a;
  return(k1*k2*k3*err);
  }

이제 목적 함수 연산 시 1, 2, 3단계 예측 오류 추산치 제곱의 합이 사용됩니다.

또한, 해당 클래스를 기반으로 위에서 언급했던 Errors_IndicatorES.mq5처럼 예측 오류 추산치를 측정할 수 있는 Erros_mod1.mq5 스크립트가 생성되었습니다. CMod1.mqh 파일과 Errors_Mod1.mq5 파일은 본문 하단에 위치한 files2.zip 파일에 포함되어 있습니다.

표 2는 기존 인디케이터와 업그레이드된 인디케이터의 예측 오류 추산치를 나타냅니다.


 MAPE1
 MAPE2
 MAPE3
 MAPE1-3
IndicatorES
 0.2099
 0.2925
 0.3564
 0.2863
Mod1
 0.2144
 0.2898
 0.3486
 0.2842


표 2. 예측 오류 측정치 비교

오류 계수인 MAPE2와 MAPE3, 그리고 평균값인 MAPE1-3이 실제로도 좀 더 낮게 나왔네요. 일단 저장 후 계속해서 수정하겠습니다.


3. 평활화 과정 매개 변수 조정

현재 값을 기준으로 평활화 매개 변수를 수정하는 것은 인풋 시퀀스 변경 시에도 평활화 계수가 최적화되도록 하기 위함입니다. 평활화 계수 조정 방법은 참고 문헌 2, 3에서 찾아볼 수 있습니다.

적응형 지수 평활화 모델을 이용하면 인디케이터의 예측 정확도가 향상될 것이므로 평활화 계수가 동적으로 변화하는 모델을 사용하도록 하겠습니다.

안타깝게도 예측 알고리즘에서 사용해 보니 대부분의 적응형 메소드가 항상 원하는 결과를 가져오지는 못하더군요. 적절한 적응형 메소드를 찾는 일은 매우 귀찮고 시간도 오래 걸리는 일입니다. 따라서 우리의 경우 참고 문헌 4번을 따라 5번에서 제시된 STES 접근법을 이용하도록 하겠습니다.

해당 접근법에 대한 설명은 참고 문헌에서 확인 가능하니 곧바로 기존 평활화 모델 수식에 적응형 평활화 계수를 적용해 보도록 하겠습니다.

 

평활화 계수 알파의 값은 알고리즘 단계별로 계산되며 예측 오류 값의 제곱값에 좌우됩니다. b와 g 계수의 값이 알파 값에 대한 예측 오류 값의 영향을 결정하죠. 나머지 수식은 기존과 동일합니다. STES 접근법에 대한 추가 설명은 참고 문헌 6번에서 찾아볼 수 있습니다.

이전 버전에서는 인풋 시퀀스별 알파 계수 최적화 값을 지정해야 했던 반면, 이제 인풋 시퀀스 평활화 과정에서 적응형 계수 b와 g가 최적화되며 알파 값이 자동으로 정해질 겁니다.

이는 CMod2 클래스를 이용해 구현됩니다. 이번에도 func 함수 관련 사항만 수정했는데요. 이제 해당 함수는 다음과 같이 나타납니다.

double CMod2::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,sb,sg,k1,k2,e,err,ae,pt,phi2,phi3,a;
  
  s=p[0]; t=p[1]; gam=p[2]; phi=p[3]; sb=p[4]; sg=p[5]; k1=1; k2=1;
  if     (gam>0.95){k1+=(gam-0.95)*200; gam=0.95;}        // Gamma   > 0.95
  else if(gam<0.05){k1+=(0.05-gam)*200; gam=0.05;}        // Gamma   < 0.05
  if     (phi>1.0 ){k2+=(phi-1.0 )*200; phi=1.0; }       // Phi     > 1.0
  else if(phi<0.05){k2+=(0.05-phi)*200; phi=0.05;}        // Phi     < 0.05
  phi2=phi+phi*phi; phi3=phi2+phi*phi*phi;
  err=0;
  for(i=0;i<Dlen-2;i++)
    {
    e=Dat[i]-(s+phi*t); err+=e*e;
    a=Dat[i+1]-(s+phi2*t); err+=a*a;
    a=Dat[i+2]-(s+phi3*t); err+=a*a;
    alp=0.05+0.9/(1+MathExp(sb+sg*e*e));                  // 0.05 < Alpha < 0.95
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  e=Dat[Dlen-2]-(s+phi*t); err+=e*e;
  a=Dat[Dlen-1]-(s+phi2*t); err+=a*a;
  alp=0.05+0.9/(1+MathExp(sb+sg*e*e));                    // 0.05 < Alpha < 0.95
  ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
  a=Dat[Dlen-1]-(s+phi*t); err+=a*a;
  return(k1*k2*err);
  }

알파 계수 값을 설정하는 수식이 약간 변경되었습니다. 해당 계수 값의 최대 및 최소 허용 값이 각각 0.05와 0.95로 설정되었습니다.

예측 오류 추산을 위해 CMod2 클래스를 기반으로 한 Errors_Mod2.mq5 스크립트가 작성됩니다. CMod2.mqh 파일과 Errors_Mod2.mq5 파일은 본문 하단의 files2.zip 파일에 포함되어 있습니다.

표 3은 스크립트 실행 결과입니다.


 MAPE1
 MAPE2
 MAPE3
 MAPE1-3
IndicatorES
 0.2099
 0.2925
 0.3564
 0.2863
Mod1
 0.2144
 0.2898
 0.3486
 0.2842
Mod2
 0.2145
 0.2832
 0.3413
 0.2797


표 3. 예측 오류 측정치 비교

적응형 평활화 계수 사용 결과 테스트 시퀀스에 대한 예측 오류 값이 약간 더 줄었습니다. 두 번의 업그레이드를 통해 오류 계수 MAPE1-3이 약 2% 감소되었죠.

큰 변화는 없었지만 일단은 여기까지만 수정하도록 하겠습니다. 다음에는 박스-칵스(Box-Cox) 변환을 이용해 보면 좋겠네요. 해당 변환은 초기 시퀀스 분포를 정규 분포와 유사하게 만드는 데에 쓰입니다.

우리의 경우, 초기 시퀀스를 변환하고, 예측 값을 산출한 후 산출된 예측 값을 재변환시킬 수 있겠죠. 변환 계수는 예측 오류 값이 최소화될 수 있도록 설정되어야 합니다. 박스-칵스 변환을 이용한 예제는 참고 문헌 7번에서 찾아볼 수 있습니다.


4. 예측 신뢰 구간

IndicatorES.mq5 인디케이터(이전 글 참조)의 예측 신뢰 구간은 특정 지수 평활화 모델에 맞는 분석 방정식을 통해 산출되었습니다. 따라서 업그레이드된 인디케이터는 기존의 인디케이터와 다른 값을 갖습니다. 평활화 계수 변수가 있기 때문에 위의 분석 방정식은 더이상 사용할 수 없습니다.

기존의 분석 방정식이 예측 오류 측정치의 분포가 좌우 대칭을 이루는 정규 분포일 것이라는 가정 때문에도 더이상 사용할 수 없겠네요. 필요 조건이 맞지 않을 뿐더러 예측 오류 분포는 정규 분포가 아닐 수도 있고 또 대칭을 이루지 않을 수도 있으니까요.

초기 인디케이터의 신뢰 구간 측정 시, 인풋 시퀀스에서부터 1단계, 2단계, 3단계.... n단계까지의 분석식을 이용한 예측 오류가 고려됩니다.

분석식을 이용하지 않고도 인풋 시퀀스에서 곧바로 예측 오류를 계산하는 방법도 있기는 합니다. 하지만 여기에는 큰 단점이 있죠. 인풋 시퀀스가 짧은 경우 신뢰 구간 추정치가 광범위하게 흩어지며 분산 및 평균의 제곱 편차 계산으로는 예상되는 오류의 정규성 관련 문제를 해결할 수 없게 됩니다.

이는 비모수 부트스트랩(리샘플링)을 통해 해결할 수 있습니다(참고 문헌 9번 참조). 핵심은 간단합니다. 초기 시퀀스에서 벗어나 무작위 샘플링(균등 분포)을 하는 경우 해당 인공 시퀀스의 분포가 초기 분포와 동일한 분포를 띤다는 것입니다.

N개의 멤버를 가진 인풋 시퀀스가 있다고 가정합니다. [0, N-1] 구간에 균등 분포를 이루는 유사 난수 시퀀스를 생성하여 초기 배열에 대한 샘플링 시 이를 인덱스로 사용하면 초기 시퀀스보다 훨씬 긴 인공 시퀀스가 생성됩니다. 이렇게 하면 생성된 시퀀스의 분포가 초기 시퀀스의 분포와 동일하거나 거의 동일한 모습을 띠죠.

신뢰 구간 측정을 위한 부트스트랩 프로시저는 다음과 같습니다.

  1. 업그레이드된 지수 평활화 모델의 인풋 시퀀스에서 모델 매개 변수의 초기 최적화 값과 해당 계수, 적응형 계수를 구합니다. 최적화 매개 변수는 Powell의 최적화 알고리즘을 이용해 산출됩니다.
  2. 산출된 최적화 매개 변수를 이용해 초기 시퀀스에 1단계 예측 오류 배열을 생성합니다. 이때 배열 내 엘리먼트의 개수는 인풋 시퀀스의 길이 N과 동일합니다.
  3. 오류 배열 내 각각의 엘리먼트에서 평균값을 뺀 오류 값을 정렬합니다.
  4. 유사 난수 시퀀스 생성기를 이용해 [0, N-1] 구간에 인덱스를 생성하고 이를 이용해 9999개의 엘리먼트로 이루어진 인공 오류 시퀀스를 형성(리샘플링)합니다.
  5. 현재 사용되는 모델의 방정식에 인공적으로 생성된 오류 배열 값을 입력해 9999개의 유사 난수 시퀀스 값을 갖는 배열을 형성합니다. 이전에는 인풋 시퀀스 값을 모델의 방정식에 대입해 예측 오류 값을 산출했다면, 이번에는 그 반대의 계산을 하는 거죠. 배열 내 각각의 엘리먼트마다 오류 값이 대입되어 입력값을 계산합니다. 그 결과, 인풋 시퀀스와 동일한 분포를 갖는, 예측 신뢰 구간을 직접 계산하기에 충분한 길이를 가진 9999개의 엘리먼트로 이루어진 배열이 탄생합니다.

이제 생성된 시퀀스를 이용해 신뢰 구간을 측정하면 됩니다. 생성된 예측 오류 배열이 오름차순을 따르는 경우, 249번과 9749번 인덱스를 갖는 배열 내 셀은 95% 신뢰 구간에 해당하는 값을 갖게 됩니다.

예측 구간을 보다 정확하게 측정하려면 홀수 길이를 갖는 배열을 이용하는 것이 좋습니다. 우리의 경우 예측 신뢰 구간의 한계는 다음과 같이 측정됩니다.

  1. 기존 설정된 최적화 모델 매개 변수를 이용해 생성된 시퀀스로 9999개의 1단계 예측 오류 값을 갖는 배열을 형성합니다.
  2. 결과 배열을 정렬합니다.
  3. 정렬된 배열에서 249번과 9749번 인덱스를 갖는 값을 선택합니다. 이는 95% 신뢰 구간을 나타냅니다.
  4. 2단계 이상의 예측 오류 측정이 필요한 경우 앞의 세 단계를 반복합니다.

이런 접근법에는 장점과 단점이 공존하는데요.

장점 가운데 하나는 예측 오류 값의 분포에 대해 생각할 필요가 없다는 것입니다. 정규 분포를 따르거나 대칭을 이룰 필요가 없죠. 또한 사용 모델에 대한 분석식을 만들기 어려울 때 적용하기 좋은 방법이기도 합니다.

단점으로는 연산 범위가 크게 확장된다는 것과 예측 오류 값이 유사 난수 시퀀스 생성기의 능력에 좌우된다는 점이 있겠네요.

해당 접근법은 꽤 원시적인 방법이므로 개선의 여지가 큽니다. 다만 우리의 경우 시각적 평가 목적으로 신뢰 구간이 필요한 것이므로 이 정도 정확도만으로도 충분한 것이죠.

 

5. 기존 인디케이터 수정 결과

기존의 인디케이터를 업그레이드한 ForecastES.mq5 인디케이터가 완성되었습니다. 유사 난수 시퀀스 생성기를 이용해 리샘플링을 진행했습니다. 기존의 MathRand() 생성기로는 덜 만족스러운 결과가 도출되었는데요. 아마 생성된 구간 [0, 32767]이 충분히 넓지 못했기 때문일 겁니다.

ForecastES.mq5 인디케이터 컴파일 시 PowellsMethod.mqh 파일과 CForeES.mqh 파일 그리고 RNDXor128.mqh 파일은 인디케이터와 동일한 디렉토리에 저장되어야 합니다. 해당 파일은 모두 fore.zip 파일에 첨부되어 있습니다.

아래는 ForecastES.mq5 인디케이터의 소스 코드입니다.

//+------------------------------------------------------------------+
//|                                                   ForecastES.mq5 |
//|                                          Copyright 2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright   "2012, victorg."
#property link        "https://www.mql5.com"
#property version     "1.02"
#property description "Forecasting based on the exponential smoothing."

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"           // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"             // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"             // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CForeES.mqh"
#include  "RNDXor128.mqh"

#define   NFORE 12
#define   NBOOT 9999

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[],Err[],BSDat[],Damp[NFORE],BSErr[NBOOT];
int       NDat;

CForeES   Es;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   NDat=nHist; if(NDat<24)NDat=24;
   MqlRates rates[];
   CopyRates(NULL,0,0,NDat,rates);                 // Load missing data
   ArrayResize(Data,NDat);
   ArrayResize(Err,NDat);
   ArrayResize(BSDat,NBOOT+NFORE);

   SetIndexBuffer(0,Hist,INDICATOR_DATA);
   PlotIndexSetString(0,PLOT_LABEL,"History");
   SetIndexBuffer(1,Fore,INDICATOR_DATA);
   PlotIndexSetString(1,PLOT_LABEL,"Forecast");
   PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
   SetIndexBuffer(2,Conf1,INDICATOR_DATA);         // Confidence interval
   PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
   PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
   SetIndexBuffer(3,Conf2,INDICATOR_DATA);         // Confidence interval
   PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
   PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
   IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
   int i,j,k,start;
   double s,t,alp,gam,phi,sb,sg,e,f,a,a1,a2;

   if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
   if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
   start=rates_total-NDat;
//-----------------------
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
   PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
   PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
   PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);

   for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
   Es.CalcPar(Data);                                    // Optimization of parameters
   s=Es.GetPar(0); t=Es.GetPar(1); gam=Es.GetPar(2);
   phi=Es.GetPar(3); sb=Es.GetPar(4); sg=Es.GetPar(5);
//----
   a=phi; Damp[0]=phi;
   for(j=1;j<NFORE;j++){a=a*phi; Damp[j]=Damp[j-1]+a;}  // Phi table
//----
   f=s+phi*t;
   for(i=0;i<NDat;i++) // History
     {
      e=Data[i]-f; Err[i]=e;
      alp=0.05+0.9/(1+MathExp(sb+sg*e*e));               // 0.05 < Alpha < 0.95
      a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
      f=(s+phi*t); Hist[start+i]=f;                      // History
     }
   for(j=0;j<NFORE;j++)Fore[rates_total-NFORE+j]=s+Damp[j]*t;  // Forecast
//----
   a=0;
   for(i=0;i<NDat;i++)a+=Err[i];
   a/=NDat;
   for(i=0;i<NDat;i++)Err[i]-=a;                       // alignment of the array of errors
//----
   f=Es.GetPar(0)+phi*Es.GetPar(1);
   for(i=0;i<NBOOT+NFORE;i++) // Resampling
     {
      j=(int)(NDat*Rnd.Rand_01());
      if(j>NDat-1)j=NDat-1;
      e=Err[j];
      BSDat[i]=f+e;
      alp=0.05+0.9/(1+MathExp(sb+sg*e*e));               // 0.05 < Alpha < 0.95
      a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
      f=s+phi*t;
     }
//----
   for(j=0;j<NFORE;j++) // Prediction intervals
     {
      s=Es.GetPar(0); t=Es.GetPar(1);
      f=s+phi*t;
      for(i=0,k=0;i<NBOOT;i++,k++)
        {
         BSErr[i]=BSDat[i+j]-(s+Damp[j]*t);
         e=BSDat[i]-f;
         a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
         f=(s+phi*t);
        }
      ArraySort(BSErr);
      Conf1[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[249];
      Conf2[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[9749];
     }
   return(rates_total);
  }
//-----------------------------------------------------------------------------------

이해를 돕기 위해 인디케이터는 최대한 직선 프로그램으로 구성했습니다. 최적화 단계는 포함되어 있지 않습니다.

그림 1과 2는 두 개의 인디케이터 연산 결과를 나타냅니다.

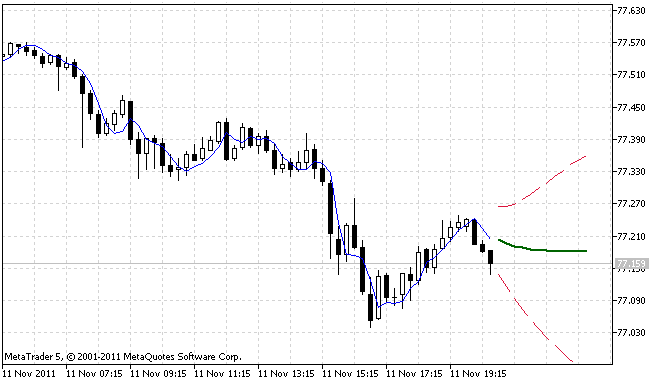
ForecastES.mq5 인디케이터 연산 예제 1

 그림 1. ForecastES.mq5 인디케이터 연산 예제 1

 ForecastES.mq5 인디케이터 연산 예제 2

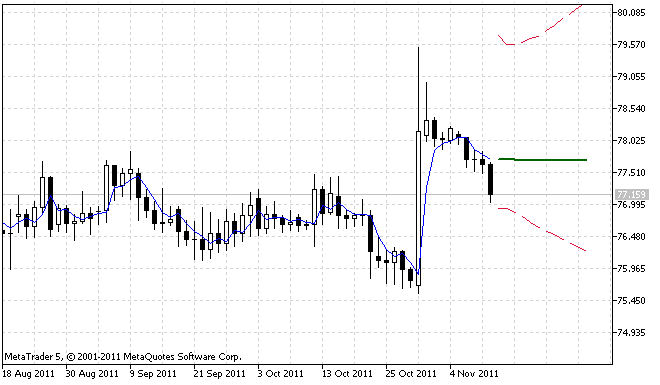
그림 2. ForecastES.mq5 인디케이터 연산 예제 2

그림 2를 보면 95% 신뢰 구간이 대칭을 이루지 않는다는 것을 확실히 알 수 있죠. 인풋 시퀀스가 꽤 많은 극단값을 가지고 있음을 의미합니다. 예측 오류 값이 불규칙적으로 분포된 것이죠.

www.mql4.com과 www.mql5.com에서 보외법이 적용된 인디케이터를 다운로드할 수 있습니다. 그 중 하나를 이용해 보죠. ar_extrapolator_of_price.mq5 파일을 열어 그림 3과 같이 매개 변수를 설정하여 우리가 개발한 인디케이터와 결과를 비교해 봅니다.

ar_extrapolator_of_price.mq5 인디케이터 설정

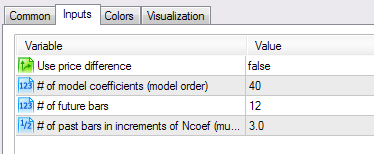
그림 3. ar_extrapolator_of_price.mq5 인디케이터 설정

두 인디케이터의 연산 결과는 EURUSD와 USDCHF 통화쌍의 서로 다른 구간에서 비교되었습니다. 겉으로 보기에는 두 인디케이터의 예측 방향이 대부분 비슷하게 나타나죠. 그러나 구간을 넓히면 디버전스가 뚜렷하게 보입니다. ar_extrapolator_of_price.mq5 인디케이터의 예측 선이 더 많이 끊기게 되죠.

그림 4는 ForecastES.mq5 인디케이터와 ar_extrapolator_of_price.mq5 인디케이터를 동시에 실행한 결과입니다.

예측 결과 비교

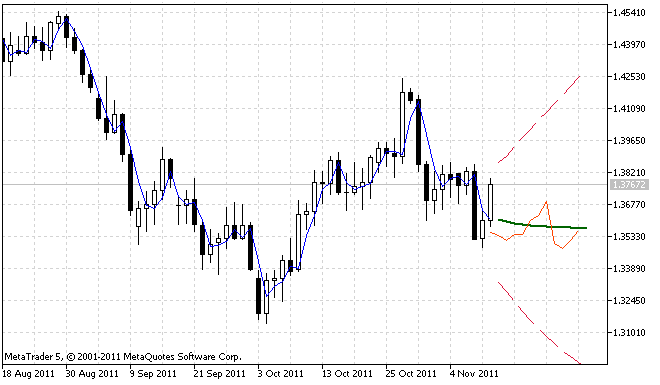
그림 4. 예측 결과 비교

ar_extrapolator_of_price.mq5 인디케이터의 예측 값이 진한 주황색 실선으로 표시되어 있습니다.

 

결론

이번 글과 지난 글을 통해 배운 내용을 요약하면 다음과 같습니다.

  • 시간열 예측에 이용되는 지수 평활화 모델 소개
  • 모델 구현 프로그래밍 방법 소개
  • 최적화 초기 값 및 모델 매개 변수 선택 관련 문제 설명
  • Powell의 알고리즘을 이용한 함수 최소화 프로그램 구현
  • 인풋 시퀀스를 이용한 예측 모델용 매개 변수 최적화 솔루션
  • 간단한 예측 알고리즘 업그레이드 방법
  • 부트스트랩과 분위수를 이용한 예측 신뢰 구간 계산 방법
  • 본문에서 설명된 모든 방법과 알고리즘이 적용된 ForecastES.mq5 예측 인디케이터 개발
  • 해당 주제와 관련된 여러 글이나 책 등도 링크해 놓았습니다.

ForecastES.mq5 인디케이터와 관련하여, Powell의 알고리즘을 이용한 최적화 알고리즘이 주어진 정확도를 만족시키는 목적 함수의 최소값을 구하지 못하는 경우도 있음에 주의하세요. 이 경우 알고리즘이 최대 실행 가능 횟수만큼 실행된 후 메세지가 나타날 겁니다. 본문에서는 필요하지 않기 때문에 따로 설명하지 않았습니다. 인디케이터 실제 적용 시에는 면밀한 모니터링이 필요합니다.

각 단계에서 여러 예측 모델을 동시에 실행한 후 아카이케 정보 기준 등을 이용해 하나의 인디케이터를 추가하는 식으로 예측 인디케이터를 한층 더 업그레이드할 수 있습니다. 혹은 비슷한 모델을 적용하는 경우 각 예측 값의 가중 평균을 계산할 수도 있겠죠. 모델별 예측 오류 계수에 따라 가중 인자를 선택하면 됩니다.

시간열 예측이 굉장히 광범위한 주제라 본문에서 깊게 다루지 못한 부분이 많아 아쉽네요. 제가 쓰는 글들이 관련 주제에 대한 여러분들의 관심을 키울 기회가 되었으면 합니다.


참고 문헌

  1. '지수 평활법을 이용한 시계열 예측'
  2. Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
  3. S.V. Bulashev. Statistics for Traders. - М.: Kompania Sputnik +, 2003. - 245 pp.
  4. Everette S. Gardner Jr., Exponential Smoothing: The State of the Art – Part II. June 3, 2005.
  5. James W. Taylor, Smooth Transition Exponential Smoothing. Journal of Forecasting, 2004, Vol. 23, pp. 385-394.
  6. James W. Taylor, Volatility Forecasting with Smooth Transition Exponential Smoothing. International Journal of Forecasting, 2004, Vol. 20, pp. 273-286.
  7. Alysha M De Livera. Automatic Forecasting with a Modified Exponential Smoothing State Space Framework. 28 April 2010, Department of Econometrics and Business Statistics, Monash University, VIC 3800 Australia.
  8. Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 January 2003.
  9. The Quantile Journal. issue No. 3, September 2007.
  10. http://ru.wikipedia.org/wiki/Квантиль
  11. '시간열 주요 특성 분석'

MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/346

파일 첨부됨 |
ZIP파일 다운로드
files2.zip (40.75 KB)
fore.zip (53.5 KB)
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기
엑스퍼트 어드바이저 비주얼 마법사로 엑스퍼트 어드바이저 만들기 엑스퍼트 어드바이저 비주얼 마법사로 엑스퍼트 어드바이저 만들기
MetaTrader 5 의 엑스퍼트 어드바이저 비주얼 마법사는 매우 직관적인 그래픽 환경과 다양한 매매 블록을 제공하여 단 몇 분만에 엑스퍼트 어드바이저를 만들 수 있도록 도와줍니다. 클릭, 드래그 앤드 드롭만 할 줄 알면 종이에 그리는 것처럼 외환 거래 전략을 시각화할 수 있습니다. 이렇게 만들어진 매매 다이어그램은 몰라니스(Molanis) MQL5 코드 생성기로 자동 분석되며 즉시 사용 가능한 엑스퍼트 어드바이저로 완성됩니다. 인터랙티브 그래픽 환경 덕분에 MQL5 코드를 쓰지 않고 간단하게 디자인할 수 있죠.
판별 분석을 이용한 매매 시스템 구축 판별 분석을 이용한 매매 시스템 구축
자동 매매 시스템을 만들다 보면 어떤 인디케이터와 어떤 신호가 가장 잘 맞을지 선택하기 어려울 때가 있습니다. 판별 분석은 인디케이터와 신호 간의 조합을 찾는 데에 도움이 되는 방법 중 하나인데요. 이 글은 시장 데이터 수집용 엑스퍼트 어드바이저 개발과 스타티스티카(Statistica)를 이용한 외환 시장(FOREX)용 예측 모델에 대한 판별 분석 적용법을 다룹니다.
트레이드미네이터 3: 라이즈 오브 더 트레이딩 머신 트레이드미네이터 3: 라이즈 오브 더 트레이딩 머신
지난 글 '닥터 트레이드러브...'에서는 미리 선택된 매매 시스템의 매개 변수를 독자적으로 최적화할 수 있는 엑스퍼트 어드바이저를 만들었습니다. 게다가 한 가지 매매 시스템의 매개 변수를 최적화할뿐만 아니라 여러 매매 시스템 가운데 가장 좋은 시스템을 선택해 주는 엑스퍼트 어드바이저까지 만들기로 했죠. 어떻게 되나 봅시다.
인디케이터 및 통계적 매개 변수 분석하기 인디케이터 및 통계적 매개 변수 분석하기
기술적 분석은 기본 시세 정보를 '보다 명확하게' 나타내는 인디케이터를 구현하여 투자자가 시장을 분석하고 가격 움직임을 예측할 수 있도록 해줍니다. 그러니 초기 시세 변동 및 획득 결과의 신뢰도와 관련된 문제를 해결할 수 없다면 인디케이터를 사용할 필요가 없겠죠. 당연히 매매 시스템에 적용할 필요도 없고요. 왜 그런지 자세히 알아보도록 하겠습니다.