시계열 주요 특성의 분석

들어가며

가격계열으로 대표되는 프로세스의 분석에는 상당한 시간과 노력이 필요한 경우가 많습니다. 연구 중인 시퀀스의 특수성과 관련이 있으며, 많은 다양한 출판물에도 불구하고 특정 문제에 대한 적절한 프로그래밍 솔루션을 찾기가 어려운 경우가 있습니다.

적합한 스크립트나 인디케이터가 발견되었다고 해도 해당 소스 코드를 당면한 작업에 맞게 조정할 필요가 없다는 뜻은 아닙니다.

더군다나 간단한 문제를 해결하는데에도 개발자는 잘 알고 있지만 사용자는 잘 알지 못하는 입력 패러미터를 사용해야 할 수 있습니다.

이러한 원인으로 인해 진지하게 연구를 하는 사람에게는 딱히 문제가 생기진 않겠지만, 만약 간단한 호기심을 충족시키고자 가볍게 접근하는 사람들에게는 지나치게 복잡해서 도움이 되지 않을 것입니다. 그래서 입력 시퀀스의 주요 특성과 패러미터를 쉽게 사전 분석할 수 있는 범용 프로그래밍 도구를 만들겠다는 생각이 들었습니다.

이러한 툴은 최대한 손쉽게 사용할 수 있게 하기 위해 입력 패러미터를 요구하지 않는 동시에 설치 또한 간단해야 합니다. 동시에 추정된 패러미터와 특성은 고려 중인 순서의 특성을 적절하고 명확하게 반영해야 합니다.

특성에 대한 예비 추정은 추가 심도 있는 연구를 위한 방법을 결정하거나 초기 단계에서 주어진 가정을 기각하고 추가 연구와 관련된 시간 손실을 방지하는 데 도움이 될 수 있습니다.

범용 소프트웨어는 종종 특화형 소프트웨어에 비해 별로라는 것이 상식이었습니다. 흔히들 보편성을 챙기는 과정에서 잃는 것이 있는데, 그런 것의 일종이죠. 하지만 이 문서를 통해 시퀀스의 특성에 대한 사전 분석을 최대한 용이하게 할 수 있는 범용 도구를 만들기 위한 노력을 보여드릴 것입니다.

설치와 처리

문서 끝에서찾으실 수 있는 TSAnalysis.zip 파일에는 이 작업에 필요한 파일들이 전부 들어있는 \TSAnalysis 폴더가 들어있습니다. 우선 압축해제를 하신 후 (이름을 변경하지 말아주세요) 이 파일들을 \MQL5\Scripts 폴더에 복사해주시기 바랍니다. 복사된 \TSAnalysis 폴더에는 컴파일 후에 실행시킬 수 있는 테스트 스크립트 TSAexample.mq5가 들어있습니다

이 스크립트는 데이터를 가공한 후 TSAnalysis 클래스를 통해 기본 브라우저를 호출, 표시합니다. TSAnalysis 클래스가 정상 작동하려면 터미널에서 외부 DLL 사용이 허가되어있어야하는 점을 유의해주시기 바랍니다. 삭제하시려면 그냥 \TSAnalysis 폴더를 지워버리시면됩니다.

시퀀스 분석에 사용되는 소스 코드는 TSAnalysis 클래스이며, TSAnalysis.mqh 파일에 들어 있습니다.

입력 시퀀스 용으로 이 클래스를 사용하실 때, 본 클래스는 다음의 정보를 추정한 후 표시합니다.

• 시퀀스 내 요소의 수;
• 시퀀스 내 최소최대값(max, min);
• 중간값;
• 평균값;
• 분산;
• 표준 편차;
• 불편분산;
• 불편표준편차;
• 왜곡도;
• 첨도;
• 초과첨도;
• 자크-베라 테스트;
• 자크-베라 테스트 p값;
• 조정 자크-베라 테스트;
• 조정 자크-베라 테스트 p값;
• 지정된 시퀀스에 속하지 않는 값에 대한 한계(아웃라이어);
• 히스토그램 데이터;
• 정규 분포 작도 데이터;
• 코렐로그램 데이터;
• 자기상관도 함수 95% 신뢰구간;
• 자기상관도 함수를 통해 계산된 스펙트럼 작도 데이터;
• 부분 자기상관도 함수 작도 데이터;
• 최대 엔트로피 방법을 사용하여 계산된 스펙트럼 추정도 데이터.

얻은 결과를 TSAnalysis 클래스를 통해 표시하기 위해 하나의 가상 메소드가 사용되는데, 이 메소드는 사전처리된 정보를 표시하는 메소드만을 담당합니다.

따라서 TS Analysis 클래스 하위 항목에서 이 방법을 재정의하면 차트를 표시하기 위한 데이터 파일을 생성할 때 웹 브라우저가 호출되는 기본 클래스와 같이 HTML 파일만 사용하는 것이 아니라 가능한 모든 방법으로 결과 출력을 정렬할 수 있습니다.

TSAnalysis 클래스에 대한 리뷰를 진행하기 전에 데이터 테스트 시퀀스를 통해 어떠한 결과가 나오는지 먼저 보여드리도록 하겠습니다. 이하의 그림을 보시면 TSAexample.mq5 스크립트 실행 결과가 나와 있습니다.

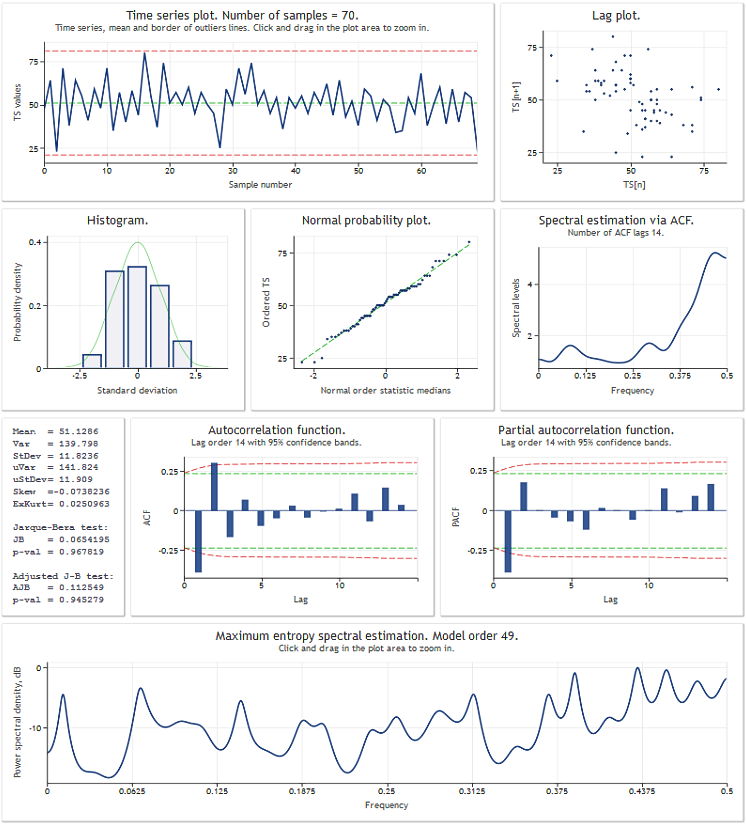
1번 그림. TSAexample.mq5 스크립트 실행 결과

TSAnalysis 클래스 처리량에 대해 간략히 숙지한 후, 이제 클래스 자체에 대해 더 자세히 알아보도록 하겠습니다.

TSAnalysis 클래스

TSAnalysis 클래스(TSAnalysis.mqh 참조)에는 사용 가능한(퍼블릭) 메소드 Calc 하나만 포함되어 있습니다. 이 메소드가 가상 메소드 show가 호출되었을 때의 모든 연산 처리를 수행합니다. show 메소드에 대해서는 이후에 다시 한 번 알아볼 것입니다. 지금은 단계별로 연산과정에 대해 알아보도록 하겠습니다.

TSAnalysis 클래스를 사용할 때엔 입력 시퀀스에는 몇가지 제약사항이 있습니다.

제일 먼저, 시퀀스에는 최소 8개의 요소가 있어야 합니다. 이 제약은 현실적으로는 그렇게 짧은 시퀀스를 사용할 일이 없기때문에 별로 상관없는 문제일 것입니다.

최소 시퀀스 길이 제약 조건 외에 입력 시퀀스 분산 값이 0에 가까워선 안된단 조건이 있습니다. 이 조건은 분산 값이 추가 계산에 사용되고 안정적인 결과를 얻기 위해서는 이 값이 특정 값보다 작아선 안되기 때문입니다.

분산 값이 매우 낮은 시퀀스는 그리 흔하지 않으므로 이 제약 조건도 심각한 단점은 아닐 수 있습니다. 시퀀스가 너무 짧고 분산 값이 0에 가까운 경우 계산이 중단되고 로그에 관련 오류 메시지가 표시됩니다.

입력 시퀀스의 최대 허용 길이와 관련하여 또 다른 제약 조건이 있습니다. 이 제약 조건은 딱 정해진 기준이 있는 것이 아니라 사용 중인 컴퓨터의 성능과 메모리 용량에 따라 달라지며, 웹 브라우저에서 스크립트 실행에 필요한 시간과 그리기 결과 속도에 따라 결정됩니다. 시퀀스 요소 수가 2~3000개 정도 까지면 아무 문제가 없을 것으로 알려져 있습니다.

시퀀스 통계 패러미터 계산은 Calc 메소드 소스 코드의 일부에 기반을 두고 있습니다(TSAnalysis.mqh 참조).

사용된 알고리즘에 대한 설명은 "Algorithms for Calculating Variance"를 참조해주시기 바랍니다.

. . .
Mean=0; sum2=0; sum3=0; sum4=0;
for(i=0;i<NumTS;i++)
  {
  n=i+1; delta=TS[i]-Mean;
  a=delta/n; Mean+=a;                                       // Mean (average)
  sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree
  b=TS[i]-Mean;
  sum3+=a*(b*delta*(n-2.0)-3.0*sum2);                       // sum of third degree
  sum2+=delta*b;                                            // sum of second degree
  }
. . .

이 스니펫의 실행에 따라 다음 값이 계산됩니다.

n = NumTS 는 시퀀스 내 요소의 갯수

얻은 값들을 이용하여 이하의 패러미터를 계산합니다.

분산 및 표준 편차:

불편분산 및 표준 편차:

왜곡도:

첨도 최소 첨도는 1이며, 정규 분포 시퀀스의 첨도는 3이 될 것입니다.

초과 첨도:

이 경우 최소 첨도는 -2이고 정규 분포 시퀀스의 첨도는 0이 됩니다.

일반적으로 시퀀스에 대해 첫 번째 예비 적합도 검정을 수행할 때 자크-베라 통계가 사용되며, 알려진 왜도 및 첨도 값을 사용하여 쉽게 계산됩니다. 시퀀스 길이가 증가할 때 Jarque-Bera 통계에 대한 통계적 유의성(p값)은 두 개의 자유도를 갖는 역 카이 제곱 분포 함수에 점근적으로 치우칩니다.

그러므로,

시퀀스가 짧은 경우, 이러한 방식으로 얻은 p값은 상당한 오차를 가질 수 있습니다. 하지만 이 계산옵션은 상당히 자주 사용됩니다. 그게 어째서인지 명료한 해답이 있는 것은 아닙니다. 어쩌면 단순하고 명확한 공식과 관련이 있거나 자크-베라 통계 자체가 이상적인 적합도 검정을 나타내지 않기 때문에 계산을 더욱 정확하게 해봤자 별 의미가 없다는 것일지도 모릅니다.

이 경우 자크-베라 통계와 관련 p값은 위의 공식에 따라 Calc 메소드(TSAnalysis.mqh)로 계산됩니다.

한편, 조정 자크-베라 테스트도 계산됩니다.

위치는

짧은 시퀀스에 대한 조정 자크-베라 테스트는 지정된 방법으로 계산된 p값의 오차를 줄이지만 완전히 없애지는 못합니다.

분석의 최종 결과에는 평균에 해당하는 선과 값이 잘못된 것으로 간주되고 지정된 순서(아웃라이어)에 속하지 않는 한계를 정의하는 선이 포함된 것으로 간주됩니다.

이런 경우 이들 한계는 다음과 같이 계산됩니다.

이 공식은 S. V. Bulashev의 저서 "Statistics for Traders"에서 P. V. Novitsky and I.A. Zograf 의 "Estimation of Error in Measurement Results" 를 인용하여 공개되었습니다. 한계를 결정한 후에는 입력 시퀀스가 처리되지 않습니다. 한계는 정보 제공용으로만 표시되어야 합니다.

입력 시퀀스 차트 외에도 입력 시퀀스 분포의 경험적 추정치를 반영하는 히스토그램을 표시하려고 합니다. 히스토그램의 인터벌 수는 다음과 같이 정의됩니다 (S. V. Bulashev "Statistics for Traders"):

결과는 가장 가까운 홀수 정수 값으로 내림됩니다. 얻은 값이 5보다 작으면 5의 값이 사용됩니다.

히스토그램의 X축 및 Y축에 대한 데이터 어레이의 요소 수는 히스토그램의 왼쪽과 오른쪽에 0 값 열이 추가되므로 얻은 구간 수에 2를 더한 값에 해당합니다.

히스토그램 작성을 위해 데이터를 준비하는 코드 스니펫(TSAnalysis.mqh 참조)이 아래에 나와 있습니다.

. . .
n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0);
if((n&0x01)==0)n--; if(n<5)n=5;                         // Number of bins
ArrayResize(XHist,n);
ArrayResize(YHist,n);
ArrayInitialize(YHist,0.0);
a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean);
if(a<b)a=b; v=Mean-a;
delta=2.0*a/n;
for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis
for(i=0;i<NumTS;i++)
  {
  k=(int)((TS[i]-v)/delta);
  if(k>(n-1))k=n-1;
  YHist[k]++;
  }
for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev;   // Histogram. Y-axis
. . .

위 코드에서

• NumTS는 시퀀스 내 요소의 수,
• XHist[] 및 YHist[]는 각각 X, Y 축 값을 담고있는 어레이,
• TSort[]는 정렬된 입력 시퀀스를 담은 어레이

이 계산 방법을 사용하면 X축 값이 표준 편차 단위로 표시되고 Y축 값이 확률 밀도에 해당합니다.

정규 분포 축으로 차트를 작성하기 위해 오름차순으로 정렬된 입력 시퀀스가 Y 축 값으로 사용됩니다. Y축과 X축 값들의 수는 같아야합니다. X축 값을 계산하려면 먼저 균등 분포 법칙에서와 같이 중간값을 찾아야 합니다.

역 정규 분포 함수를 사용하여 X축 값을 계산하는 데에도 사용됩니다(ndtri 메소드 참조).

자기상관도 함수(autocorrelation function, ACF), 부분 자기상관도 함수(partial autocorrelation function, PACF) 그림을 만들고 최대 엔트로피 방법을 사용하여 스펙트럼 추정치를 계산하려면 입력 시퀀스에 대한 자기상관도 함수 값을 찾아야 합니다.

ACF 및 PACF 그림에 표시되어야 하는 값의 수를 다음과 같이 정의합니다.

 

지정된 방법으로 결정된 값의 수는 플롯에 자기상관도 함수를 표시하는 데 충분하지만 스펙트럼 추정의 추가 계산에는 사용된 자기 회귀 모델의 순서와 동일한 ACF 값을 더 많이 계산하는 것이 바람직하다.

확보한 NLags 값에 의해 IP model 순서가 결정됩니다.

 

스펙트럼 추정을 위한 모델의 최적 순서를 결정하는 프로세스를 공식화하는 것은 매우 어렵습니다. 낮은 차수의 모델은 극히 평활한 결과를 가져오는 반면, 높은 차수의 모델은 값 범위가 큰 불안정한 스펙트럼 추정치를 초래할 가능성이 높습니다.

게다가, 모델 순서도 입력 시퀀스의 성격에 영향을 받기 때문에 위의 공식을 사용하여 결정된 IP 순서가 너무 높은 경우도 있고 너무 낮은 경우도 있습니다. 안타깝게도, 필요한 모델 순서를 판단하는 이거다할 효과적인 방법이 알려져있지 않습니다.

따라서 입력 시퀀스의 경우 시퀀스의 스펙트럼 추정에 사용되는 IP 모델 순서와 동일한 ACF 값의 수를 결정해야 한다. 

. . .
ArrayResize(cor,IP);
a=0;
for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i];    
for(i=1;i<=IP;i++)
  {  
  c=0;
  for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i];
  cor[i-1]=c/a;                                   // Autocorrelation
  }
. . .

소스 코드의 이 파트(TSAnalysis.mqh 참조)는 자기상관도 함수(ACT)를 계산하는 과정을 나타내고 있습니다. 계산 결과는 cor[] 어레이에 저장됩니다. 보시다시피, 자기상관도 계수가 0인 경우 먼저 계산되고 그 다음에 루프의 나머지 계수가 계산 및 정규화됩니다. 이러한 정규화 시 0 계수는 항상 1이 되므로 cor[] 어레이에 저장할 필요가 없습니다.

이 어레이에는 첫 번째 어레이부터 시작하는 IP와 동일한 계수 수가 포함됩니다. ACF를 계산할 때 TSCenter[] 어레이가 사용됩니다. 이 어레이에는 평균 값이 감산된 모든 요소의 입력 시퀀스가 포함됩니다.

ACF 계산에 필요한 시간을 줄이기 위해 FFT와 같은 고속 변환 알고리즘을 사용하는 방법을 사용할 수 있습니다. 그러나 이 경우 ACF를 계산하는 데 걸리는 시간이 그렇게 길지 않으므로 굳이 코드를 복잡하게 짤 필요는 없을 것입니다.

얻은 상관 계수의 값을 사용하여 ACF 그림(코렐로그램)을 쉽게 작성할 수 있습니다. 이 그래프에 95% 신뢰도 구간을 표시할 수 있도록 다음 공식을 사용하여 값을 계산할 수 있습니다.

랜덤성을 검정하는 데 사용되는 대역의 경우

 

ARIMA 모델 순서를 결정하는 대역의 경우

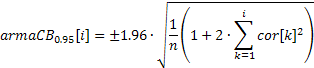
첫 번째 경우의 신뢰도 구간은 일정하며 두 번째 경우의 자기 상관 계수가 증가하면 증가합니다.

빈도 분포의 일반적인 트렌드만 반영하는 입력 시퀀스의 매우 평활화된 빈도에 관심을 가져볼 가치가 있는 경우가 있습니다. 예를 들어, 저주파 또는 고주파수 범위의 상당한 상승, 중간파수의 우세 등입니다.

이러한 주파수 응답을 선형 척도로 표시하여 지배적인 주파수 범위를 강하게 강조하는 것이 좋습니다. 이러한 진폭-주파수 반응(AFR)은 이전에 얻은 자기 상관 계수를 기반으로 표시할 수 있습니다. AFR 계산에는 ACF 그림에 표시된 수와 동일한 계수 수를 사용합니다.

이 숫자가 크지 않다는 점을 감안할 때 그 결과로 얻은 스펙트럼 추정치는 상당히 매끄러워야 합니다.

이 경우 시퀀스의 빈도 반응은 다음과 같이 자기 상관 계수를 사용하여 나타낼 수 있습니다.

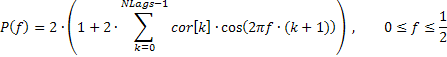
공식을 기반으로 AFR을 계산하는 데 사용되는 코드 스니펫(TSAnalysis.mqh 참조)을 아래에서 보실 수 있습니다.

. . .
n=320;                                              // Number of X-points
ArrayResize(Spect,n);
v=M_PI/n;
for(i=0;i<n;i++)
  {
  a=i*v; b=0;
  for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1));
  Spect[i]=2.0*(1+2*b);                             // Spectrum Y-axis
  }
. . .

위의 코드의 상관 계수 값은 추가 평활을 위해 삼각 창 함수에 곱한 값입니다.

보다 상세한 스펙트럼 분석을 위해 최대 엔트로피 방법을 또 다른 타협으로 선택했습니다. 보편적 스펙트럼 추정 메소드 선택은 상당히 어렵습니다. 전통적인 비모수 스펙트럼 분석 방법과 관련된 단점은 꽤나 유명합니다.

고속 푸리에 변환 알고리즘을 사용하여 쉽게 구현할 수 있는 메소드에는 피리오도그램과 코렐로그램 방법이 있습니다. 그러나 결과의 높은 안정성에도 불구하고, 이 메소드들을 이용하여 적절한 해상력을 얻기 위해서는 매우 긴 입력 시퀀스가 필요합니다. 반대로, 스펙트럼 추정의 파라메트릭 메소드(예: 자기 회귀 방법)를 이용하면 짧은 시퀀스를 가지고도 훨씬 높은 해상력을 보장합니다.

하지만 이러한 메소드들을 사용할 때엔 구현법의 특수성 뿐만 아니라 입력 시퀀스의 특수성 또한 고려해야한다는 것이 숙제입니다. 동시에 최적의 AR 모델 순서를 결정하는 것은 상당히 어려우며, 이로 인해 해상력이 증가하지만 흩어진 결과가 얻어집니다. 초고차 모델을 이용하면 이 메소드들은 불안정한 결과를 낳기 시작합니다.

각기 다른 스펙트럼 추정 알고리즘의 비교적 특성은 S. L. Marple의 저서 "Digital Spectral Analysis with Applications"에서 찾아볼 수 있습니다. 앞에서 언급한 것 처럼 우리의 경우 최대 엔트로피 메소드를 선택하였습니다. 다른 자기 회귀 방법에 비해 해상력 강도가 낮을 수 있지만 보다 안정적인 스펙트럼 추정치를 얻을 수 있기 때문에 이 메소드를 선택했습니다.

자기 회귀 스펙트럼 추정 계산 순서를 살펴봅시다. 모델 순서 선택은 앞에서 다뤄졌으니, 우리는 모델 순서가 이미 IP로 선택되었고 IP 자기상관도 계수 cor[] 가 계산되었다고 전제할 것입니다.

이미 확보한 자기상관도 계수를 사용하여 자기 회귀 계수를 얻기 위해 레빈슨-더빈 알고리즘이 LevinsonRecursion 메소드로 구현됩니다.

//-----------------------------------------------------------------------------------
// Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[]
// and return the autoregression coefficients A[] and partial autocorrelation
// coefficients K[]
//-----------------------------------------------------------------------------------
void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[])
  {
  int p,i,m;
  double km,Em,Am1[],err;

  p=ArraySize(R);
  ArrayResize(Am1,p);
  ArrayInitialize(Am1,0);
  ArrayInitialize(A,0);
  ArrayInitialize(K,0);
  km=0;
  Em=1;
  for(m=0;m<p;m++)
    {
    err=0;
    for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1];
    km=(R[m]-err)/Em;
    K[m]=km; A[m]=km;
    for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]);
    Em=(1-km*km)*Em;
    ArrayCopy(Am1,A);
    }
  return;
  }

이 메소드에는 3개의 입력 패러미터가 있습니다. 이들 패러미터는 어레이로의 레퍼런스입니다. 이 메소드를 호출할 때는 입력 자기상관도 계수를 첫 번째 어레이 R[]에 넣어야 합니다. 계산 과정에서 이들의 값은 변하지 않습니다.

얻어진 자기상관도 계수는 A[] 어레이에 배치됩니다. K[] 어레이에는 반대 부호로 취한 자기 회귀 모형 반사 계수와 같은 부분 자기상관도 함수 값이 포함됩니다. 모델 순서는 입력 패러미터로서 전달되지 않습니다. 입력 어레이 R[]의 요소수와 같다고 전제되기 때문입니다.

따라서 출력 어레이 크기는 입력 어레이 크기 이상이어야 합니다. 이 부분이 준수되고 있는지에 대해서 함수내에서 확인하지는 않습니다. 계산을 완료해도 부분 자기상관도 함수의 자기 회귀 계수 0과 계수가 A[]와 K[] 어레이에 저장되지 않습니다.

그 값들은 언제나 1과 같다고 전제됩니다. 따라서 출력 어레이는 입력 순서와 마찬가지로 1부터 IP까지의 인덱스를 가진 계수를 포함합니다(0부터 시작하는 어레이 인덱스와 혼동하지 마십시오).

얻어진 부분 자기상관도 함수의 값은 각 그림에 위치를 표시하는 경우에만 사용되며, 자기 회귀 계수는 다음 공식으로 정의된 주파수 반응 추정치의 계산의 기초가 됩니다.

빈도 응답은 0 ~ 0.5 범위에 걸쳐 4096개의 빈도 주파수 값에 대해 계산됩니다. 위의 공식을 사용하여 AFR 값을 직접 계산하는 데는 시간이 너무 많이 소요되며, 복잡한 지수 합계를 계산하기 위해 고속 푸리에 변환 알고리즘을 사용하면 상당히 줄일 수 있습니다.

바로 그 이유로 Calc 메소드에서는 고속 푸리에 변환 대신 고속 하틀리 변환(FHT)을 사용합니다.

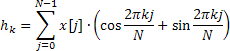
하틀리 변환은 복잡한 연산을 포함하지 않으며 입력 및 출력 시퀀스가 모두 유효합니다. 역 하틀리 변환은 추가 팩터 1/N만 필요로 하는 동일한 공식을 사용하여 계산됩니다.

유효한 입력 시퀀스에서는 이 변환의 계수와 푸리에 변환의 계수 사이에 단순한 연결이 있습니다.

 

고속 하틀리 변환에 대한 정보는 "FXT algorithm library" 및 "Discrete Fourier and Hartley Transforms"에서 찾아보실 수 있습니다 .

위 구현에서 고속 하틀리 변환 함수는 fht 메소드로 표현됩니다.

//-----------------------------------------------------------------------------------
// Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT).
// Length is N = 2 ** ldn
//-----------------------------------------------------------------------------------
void TSAnalysis::fht(double &f[], ulong ldn)
  {
  const ulong n = ((ulong)1<<ldn);
  for (ulong ldm=ldn; ldm>=1; --ldm)
    {
    const ulong m = ((ulong)1<<ldm);
    const ulong mh = (m>>1);
    const ulong m4 = (mh>>1);
    const double phi0 = M_PI / (double)mh;
    for (ulong r=0; r<n; r+=m)
      {
      for (ulong j=0; j<mh; ++j)
        {
        ulong t1 = r+j;
        ulong t2 = t1+mh;
        double u = f[t1];
        double v = f[t2];
        f[t1] = u + v;
        f[t2] = u - v;
        }
      double ph = 0.0;
      for (ulong j=1; j<m4; ++j)
        {
        ulong k = mh-j;
        ph += phi0;
        double s=MathSin(ph);
        double c=MathCos(ph);
        ulong t1 = r+mh+j;
        ulong t2 = r+mh+k;
        double pj = f[t1];
        double pk = f[t2];
        f[t1] = pj * c + pk * s;
        f[t2] = pj * s - pk * c;
        }
      }
    }
  if(n>2)
    {
    ulong r = 0;
    for (ulong i=1; i<n; i++)
      {
      ulong k = n;
      do {k = k>>1; r = r^k;} while ((r & k)==0);
      if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;}
      }
    }
  }

이 메소드를 호출할 때 입력 데이터 배열 f[] 및 변환 길이 N = 2 ** ldn을 정의하는 부호 없는 정수 ldn에 대한 참조가 입력에 전달됩니다. 어레이 f[]의 크기는 변환 길이 N보다 작으면 안 됩니다. 함수 내부에서는 변환 길이를 확인할 수 없습니다. 변환 결과는 입력 데이터가 있는 어레이에 저장되는 것을 기억해두시기 바랍니다.

변환 후 입력 데이터 자체는 저장되지 않습니다. 고려 중인 계산 방법에서는 길이 N=8192의 변환을 사용하여 4096 개의 AFR 값을 계산합니다. 변환 크기 제곱을 계산하고 역수를 구하면 얻은 결과가 최대값으로 정규화되고 로그 스케일링됩니다.

그 외에는 Calc 메소드만의 특징은 딱히 없으며, 필요한 경우 TSAnalysis.mqh 파일을 참고하시어 Calc 메소드를 구현을 자세히 살펴볼 수 있습니다.

계산 후 표시용으로 얻어진 모든 결과 값은 TSAnalysis 클래스의 구성요소인 변수들에 저장됩니다. 따라서 결과를 표시하기 위해 가상 메소드 show를 호출할 때 인수로 전달되지 않아도 됩니다.

시각화

앞서 말했 듯이 show 메소드는 가상으로 선언되었습니다. 따라서 이를 재정의함으로써 제안된 계산 결과와 다른 계산 결과를 표시하는 데 필요한 메소드를 구현할 수 있습니다. 제안된 TSAnalysis 클래스의 시각화는 데이터 파일 준비 및 데이터 표시를 위한 웹 브라우저를 호출하여 수행됩니다.

웹 브라우저가 이러한 데이터를 표시할 수 있도록 TSA.htm 파일이 나머지 프로젝트 파일과 동일한 디렉토리에 위치하게됩니다. 그래픽 정보를 표시하는 용도의 본 메소드에 대한 설명은 "Graphs and Diagrams in HTML" 문서에서 찾아보실 수 있습니다.

show 메소드의 TSAnalysis 클래스는 표시할 모든 계산 결과를 스트링 타입 변수로 포맷하고 저장하는 역할을 담당합니다(TSAnalysis.mqh 참조). 이 과정에서 생성된 긴 줄들은 한 번에 TSDat.txt에 저장됩니다. 표준 MQL 툴을 사용하여 파일을 생성하고 데이터를 이 안에 저장하는 과정이 이루어지며, 파일은 \MQL5\Files 디렉토리에 생성됩니다.

그런 다음 외부 시스템 기능을 호출하여 이 파일을 이 프로젝트의 디렉토리로 이동합니다. 이어서 TSDat.txt에서 데이터를 받아오는 TSA.htm을 표시하는 웹 브라우저가 호출됩니다. show 메소드에서 시스템 함수들을 호출하므로, TSAnalysis 클래스와의 연동을 위해선 터미널에서 외부 DLL을 사용허가를 선행해두어야 합니다.

예시

TSAnalysis.zip 아카이브에 들어있는 TSAexample.mq5은 TSAnalysis 클래스의 사용 예시입니다.

//-----------------------------------------------------------------------------------
//                                                                     TSAexample.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "TSAnalysis.mqh"
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50,
  60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52,
  38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23};

  TSAnalysis *tsa=new TSAnalysis;

  tsa.Calc(bd);

  delete tsa;

  }

보다시피 클래스에 대한 참조는 매우 간단합니다. 입력 시퀀스가 포함된 어레이가 준비되어 있다면 분석용도로 쉽게 Calc 메소드로 전달할 수 있습니다. 덤으로 delete를 호출하여 메모리를 비우는 것도 잊지마셔야합니다. 이 스크립트 실행 결과는 이 문서 앞쪽에서 이미 보셨을 겁니다..

생성된 스펙트럼 추정치의 효율성을 입증하기 위해 생성된 시퀀스를 사용해볼 추가 예시들을 살펴봅시다.

먼저 두 사인파를 담고 있는 시퀀스를 사용해봅시다.

int i,n;
double a,x[];
  
n=400;
ArrayResize(x,n);
a=2*M_PI;
for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);

아래 그림은 이 시퀀스의 진동수 반응 추정치를 보여줍니다.

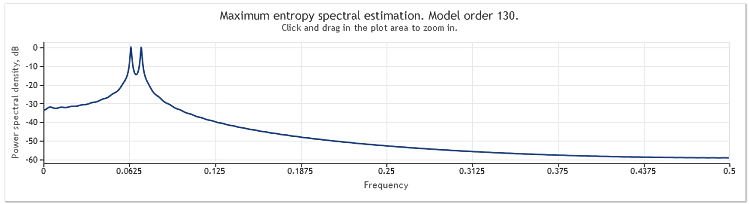
2번 그림. 스펙트럼 추정 두개의 사인파

두 사인파를 모두 잘 관찰할 수 있지만 관심 차트 영역을 확대하면 피크가 0.0637 및 0.0712의 진동수에 위치함을 알 수 있습니다. 다시 말해 이들은 실제 값과는 조금 차이가 있습니다. 시퀀스가 단일 사인파로 구성된 경우, 추정치에서 그러한 편향이 나타나지 않습니다. 이것이 우리가 선택한 특정 스펙트럼 분석 메소드의 영향으로 일어났다고 생각하게됩니다.

이제 시퀀스에 임의의 구성요소를 추가함으로써 작업을 더욱 복잡하게 만들 것입니다. 이 목적으로 쓰일 의사 임의 시퀀스 생성기는 문서 끝에 첨부된 RNDXor128.zip 아카이브에 들어있는 RNDXor128 클래스로 표현됩니다.

아래 코드 스니펫을 사용하여 테스트 신호를 생성했습니다.

int i,n;
double a,x[];
  
RNDXor128 *rnd=new RNDXor128;
n=800;
ArrayResize(x,n);
a=2*M_PI;
for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm();
delete rnd;

이 예시에서는 정규 분포와 단위 분산을 갖는 랜덤 신호를 두 개의 사인파에 추가했습니다.

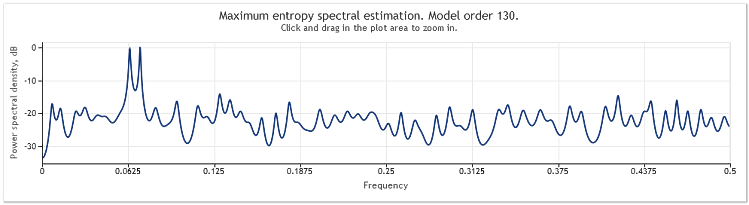
3번 그림. 스펙트럼 추정 두 사인파와 랜덤 신호

이 경우 사인파 성분이 잘 식별됩니다.

임의 성분의 진폭이 5배 증가하면 실질적으로 마스킹된 사인파가 생성됩니다.

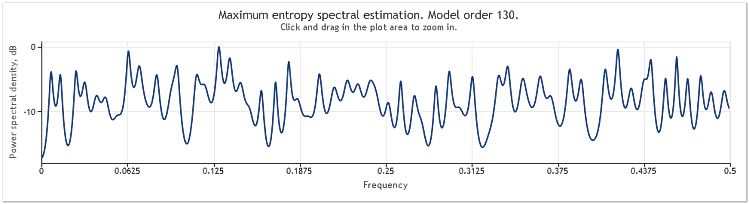
4번 그림. 스펙트럼 추정 2개의 사인파 + 진폭이 큰 랜덤 신호

시퀀스 길이가 400개에서 800개로 증가하면 사인파가 다시 잘 관찰됩니다.

 

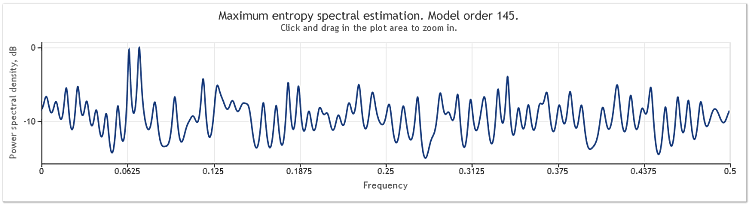
5번 그림. 2개의 사인파 + 진폭이 큰 랜덤 신호 N=800

따라서 자기 회귀 모형 순서는 130에서 145로 증가했습니다. 시퀀스 길이가 증가하면 모형이 고차원으로 변경되며 그 결과 스펙트럼 추정치의 해상도가 증가하여 차트 피크가 현저하게 더 선명해집니다.

2년(2009년 및 2010년) 동안 EURUSD, D1에 대한 견적에 대한 스펙트럼 추정치는 다음과 같습니다.

6번 그림. EURUSD 결과. 2009-2010. D1 기간

입력 순서는 519개의 값으로 구성되었으며, 그림에서와 같이 모델 순서는 135로 나타났습니다.

볼 수 있듯이, 이 스펙트럼 추정치에는 여러 가지 뚜렷한 피크가 포함되어 있습니다. 그러나 이러한 추정만으로는 이러한 피크가 견적에서 주기적인 구성요소인지 여부를 확인하는 데 충분하지 않습니다.

주파수 응답의 피크 발생은 따옴표에 있는 높은 수준의 랜덤 구성요소 또는 해당 시퀀스의 명시적 비정지 상태에 의해 발생할 수 있습니다.

따라서 주기적인 구성요소의 존재에 관한 결론을 도출하기 전에 항상 시퀀스의 다른 부분이나 다른 기간의 데이터를 사용하여 얻은 결과를 검증하는 것이 바람직합니다. 또한, 순환재발을 연구할 때, 순서 그 자체 대신 순서 차이를 이용해 볼 수 있습니다.

 

마치며

이 문서에 사용한 스펙트럼 추정 방법은 자기 상관 계수에 기초하기 때문에 입력 시퀀스의 평균은 항상 방법을 적용할 때 시퀀스에서 삭제되는 것으로 보입니다. 입력 시퀀스에서 상수 구성요소를 삭제해야 하는 경우가 많지만, 자기 회귀 방법을 사용할 경우 그러한 삭제는 저주파 범위에서 스펙트럼 추정치의 왜곡을 유발할 수 있습니다.

그런 왜곡의 예시는 S. L. Marple의 저서 "Digital Spectral Analysis with Applications"의 "Summary of Results Regarding Spectral Estimates" 챕터 끝에서 확인해볼 수 있습니다. 우리의 경우, 이미 스펙트럼 분석 방법을 정해버렸으니 다른 선택의 여지가 없고, 스펙트럼 추정은 항상 삭제된 평균을 가진 시퀀스에 대해 수행된다는 점을 유념해야 합니다.

참조

• Wuertz, Diethelm and Katzgraber, Helmut (2009): Precise finite-sample quantiles of the Jarque-Bera adjusted Lagrange multiplier test, Swiss Federal Institute of Technology, Zurich,2009.
• Tanweer-ul-Islam, Asad Zaman, Normality Testing - A new Direction, IIE, International Islamic University, Islamabad, Pakistan, 2008.
• Carlos M. Urzua, Portable and powerful tests for normality, Tecnologico de Monterrey, Campus Ciudad de Mexico, 2007.
• Comparison of Common Tests for Normality
• S. V. Bulashev. Statistics for Traders. - М.: Kompania Sputnik +, 2003. - 245 pp.
• P. V. Novitsky, I. A. Zograf. Estimation of Error in Measurement Results. Energoatomizdat, 1991.
• S. L. Marple, Jr. Digital Spectral Analysis with Applications. Moscow: Mir, 1990.
• David J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures, Chapman and Hall/CRC.