Implementando el algoritmo de aprendizaje ARIMA en MQL5

Introducción

La mayoría de los tráders de divisas y criptomonedas que buscan explotar movimientos a corto plazo sufren una falta de información fundamental. En este caso, los métodos estándar de series temporales pueden servir de ayuda. George Box y Gwilym Jenkins desarrollaron el que quizá sea el método de pronóstico de series temporales más popular. Si bien se han realizado mejoras en el método a lo largo del tiempo, sus principios básicos siguen resultando relevantes en la actualidad.

Uno de los derivados del método es el modelo autorregresivo integrado de media móvil (ARIMA), que se ha convertido en un método popular de predicción de series temporales. Esta es una clase de modelos que captura las dependencias temporales en una serie de datos y ofrece un marco para modelar series temporales no estacionarias. En este artículo, tomaremos el método de minimización de funciones de Powell como base para crear un algoritmo de aprendizaje ARIMA utilizando el lenguaje de programación MQL5.

Descripción general de ARIMA

Box y Jenkins argumentaron que la mayoría de las series temporales se pueden modelar con una o ambas estructuras. Una de ellas es la autorregresión (AR), que indica que el valor de una serie se puede explicar con respecto a sus valores anteriores, junto con un desplazamiento constante y una pequeña diferencia, comúnmente denominada innovación o ruido. Tenga en cuenta que en este texto nos referiremos al componente de ruido o error como innovación. La innovación explica la variación aleatoria que no se puede explicar de otras formas.

La segunda estructura subyacente al modelo ARIMA es la media móvil (MA). Este modelo establece que el valor de una serie supone la suma proporcional de un cierto número de condiciones de innovación previas, la innovación actual y, nuevamente, un desplazamiento constante. Existen muchas otras condiciones estadísticas que determinan estos patrones, pero no entraremos en detalles. Mucha información necesaria se puede encontrar en Internet, pero a nosotros nos interesa más su aplicación.

No nos limitaremos a los modelos MA y AR puros, podemos combinarlos para crear modelos mixtos llamados modelos de media móvil autorregresiva (Autoregressive Moving Average, ARMA). En el modelo ARMA, especificamos un número finito de series de retraso y los términos de ruido (noise terms) además de un desplazamiento constante y un término de innovación actual.

Uno de los requisitos fundamentales que rige la aplicación de todas estas estructuras es que la serie modelada debe ser estacionaria. Dependiendo de lo rigurosa que sea nuestra definición de estacionariedad, los modelos descritos hasta ahora resultan técnicamente inadecuados para su aplicación a series temporales financieras. Aquí es donde ARIMA viene al rescate: la integración matemática es lo opuesto a la diferenciación. Cuando una serie temporal no estacionaria se diferencia una o más veces, la serie resultante suele tener una mejor estacionariedad. Al diferenciar la serie por primera vez, podemos aplicar estos modelos a la serie resultante. La I en ARIMA se refiere a la necesidad de integrar la diferenciación aplicada para retornar la serie simulada al dominio original.

Descripción del modelo autorregresivo

Existe una descripción estándar del modelo. El número de componentes AR (sin contar el componente permanente) por lo general se denomina p. Los componentes de MA se denotan como q, y d describe cuántas veces se ha diferenciado la serie original. Usando estos términos, un modelo ARIMA se define como ARIMA(p, d, q). Los procesos puros pueden representarse como MA(q) y AR(p). Los modelos mixtos sin diferencias se escriben como ARMA(p,q). Esta notación presupone que los constituyentes son contiguos. Por ejemplo, ARMA (4,2) indica que la serie puede describirse mediante 4 términos AR consecutivos y los dos términos de innovación consecutivos anteriores. Usando ARIMA, podremos representar procesos puros estableciendo p, q o d en cero. Por ejemplo, ARIMA(1,0,0) se reducirá a un modelo AR(1) puro.

La mayoría de los modelos autorregresivos indican que los términos correspondientes son continuos, desde el retraso 1 hasta el retraso p y el retraso q para los términos AR y MA, respectivamente. El algoritmo que mostraremos permitirá especificar retrasos no adyacentes para los componentes MA y/o AR. Otra elemento de flexibilidad que aportará el algoritmo es la capacidad de especificar modelos con o sin desplazamiento constante.

Por ejemplo, será posible construir modelos definidos por la siguiente función:
                                 

                                                        y(t) = AR1* y(t-4) + AR2*y(t-6) + E(t)         (1)

La función anterior describe un proceso AR(2) puro sin desplazamiento constante, con el valor actual determinado por los valores de la serie de hace 4 y 6 intervalos temporales anteriores. La descripción estándar no ofrece una manera de especificar dicho modelo, pero no deberíamos vernos limitados por tales restricciones.
 

Cálculo de los coeficientes del modelo y el desplazamiento constante.

El modelo puede tener coeficientes p+q que debemos calcular. Para hacer esto, usaremos la especificación del modelo para predecir los valores conocidos de la serie, luego compararemos los valores predichos con los valores conocidos y calcularemos la suma de los errores cuadráticos. Los coeficientes óptimos serán aquellos que ofrezcan la menor suma de errores cuadráticos.

Debemos tener precaución en las previsiones, por las limitaciones que impone la indisponibilidad de datos, que se extienden hasta el infinito. Si hay componentes AR en la especificación del modelo, podremos comenzar a hacer predicciones solo después del número de valores que corresponda al mayor retraso de todos los componentes AR.

Usando el ejemplo anterior (1), solo podremos comenzar a hacer predicciones a partir del intervalo temporal 7, ya que cualquier predicción anterior se referirá a valores desconocidos antes del inicio de la serie.

Cabe señalar que si (1) tuviera componentes MA, entonces en este punto el modelo se consideraría puramente autorregresivo, ya que aún no tenemos una serie de innovaciones. Una serie de valores de innovación se generarán a medida que se hagan proyecciones futuras. Volviendo al ejemplo, el primer pronóstico en el séptimo intervalo temporal se calculará con coeficientes AR iniciales arbitrarios.

 La diferencia entre la predicción calculada y el valor conocido en el séptimo intervalo temporal será la innovación para este intervalo. Si se especifica algún componente MA, se incluirá en el cálculo del pronóstico conforme se conozcan los retrasos de innovación correspondientes. De lo contrario, los componentes MA simplemente se pondrán a cero. En el caso de un modelo MA puro, se sigue un procedimiento similar, excepto que esta vez, si es necesario incluir un desplazamiento constante, se inicializará como el valor promedio de la serie.

El método descrito tiene solo una limitación obvia. La serie conocida debe contener una cantidad proporcional de valores en relación al orden en que se aplica el modelo. Cuantos más componentes y/o mayor sea el retraso de estos componentes, más valores necesitaremos para ajustarnos al modelo de forma eficaz. El proceso de aprendizaje se completará aplicando el algoritmo de minimización global correspondiente para optimizar los coeficientes. El algoritmo que usaremos para minimizar el error de predicción se conoce como método de Powell. Las características de implementación utilizadas aquí se describen en el artículo "Predicción de series de tiempo usando el ajuste exponencial".

Clase CArima

El algoritmo de aprendizaje ARIMA se encontrará en la clase CArima en Arima.mqh. La clase tiene dos constructores, cada uno de los cuales inicializa el modelo autorregresivo. El constructor predeterminado crea un modelo AR(1) puro con desplazamiento constante.

CArima::CArima(void)
  {
   m_ar_order=1;
//---
   ArrayResize(m_arlags,m_ar_order);
   for(uint i=0; i<m_ar_order; i++)
      m_arlags[i]=i+1;
//---
   m_ma_order=m_diff_order=0;
   m_istrained=false;
   m_const=true;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

El constructor parametrizado ofrece más control sobre cómo se define el modelo. Se requieren cuatro argumentos que enumeramos a continuación:

Parámetros	Tipo de parámetro	Descripción de los parámetros
p	entero sin signo	número de componentes AR para el modelo
d	entero sin signo	especifica el grado de diferencia aplicado a la serie simulada
q	entero sin signo	Indica el número de componentes MA que debe contener el modelo.
use_const_term	bool	establece el uso de un desplazamiento constante en el modelo

CArima::CArima(const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }


   m_istrained=false;
   m_const=use_const_term;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

Además de los dos constructores proporcionados, el modelo también se puede especificar usando uno de los métodos Fit() sobrecargados. Ambos métodos toman la serie de datos simulados como primer argumento. El método Fit() tiene solo un argumento, mientras que el segundo requiere cuatro argumentos más: todos ellos son idénticos a los ya documentados en la tabla anterior.

bool CArima::Fit(double &input_series[])
  {

   uint input_size=ArraySize(input_series);

   uint in = m_ar_order+ (m_ma_order*2);

   if(input_size<=0 || input_size<in)
      return false;

   if(m_diff_order)
      difference(m_diff_order,input_series,m_differenced,m_leads);
   else
      ArrayCopy(m_differenced,input_series);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   double parameters[];
   ArrayResize(parameters,(m_const)?m_ar_order+m_ma_order+1:m_ar_order+m_ma_order);
   ArrayInitialize(parameters,0.0);

   int iterations = Optimize(parameters);

   if(iterations>0)
      m_istrained=true;
   else
      return false;

   m_sse=PowellsMethod::GetFret();

   ArrayCopy(m_model,parameters);

   return true;

  }

El uso de un método con más parámetros sobrescribirá cualquier modelo que se haya especificado previamente y también supondrá que los retrasos de los componentes están uno al lado del otro. Ambos supondrán que la serie de datos especificada como primer parámetro no está diferenciada. Por lo tanto, se aplicará la diferenciación si así se indica en los parámetros del modelo. Ambos métodos retornan un valor booleano que indica el éxito o el fracaso del proceso de entrenamiento del modelo.

bool CArima::Fit(double&input_series[],const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }

   m_istrained=false;
   m_const=use_const_term;

   ZeroMemory(m_innovation);
   ZeroMemory(m_model);
   ZeroMemory(m_differenced);

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);

   return Fit(input_series);

  }

En cuanto a la configuración de los retrasos para los componentes AR y MA, la clase ofrece los métodos SetARLags() y SetMALags(), respectivamente. Ambos funcionan de la misma forma, tomando un único argumento de array cuyos elementos deberán ser los retrasos correspondientes para el modelo ya establecido por uno de los constructores. El tamaño del array deberá coincidir con el orden correspondiente de los componentes AR o MA. Los elementos del array podrán contener cualquier valor mayor o igual a uno. Veamos un ejemplo de especificación de un modelo con retrasos AR y MA no adyacentes.

El modelo que queremos construir está determinado por la función que vemos abajo:
         

                                        y(t) = AR1*y(t-2) + AR2*y(t-5) + MA1*E(t-1) + MA2*E(t-3) + E(t)                 (2)

Este modelo está definido por el proceso ARMA(2,2) usando retrasos AR iguales a 2 y 5 y retrasos MA iguales a 1 y 3.
El siguiente código muestra cómo podemos indicar dicho modelo.

CArima arima(2,0,2);

uint alags [2]= {2,5};
uint mlags [2]= {1,3};

if(arima.SetARLags(alags) && arima.SetMALags(mlags))
   Print(arima.Summary());

Después de ajustar exitosamente un modelo a una serie de datos usando uno de los métodos Fit(), los coeficientes óptimos y el desplazamiento constante se pueden obtener llamando al método GetModelParameters(). Se requiere un argumento de array para almacenar todos los parámetros del modelo optimizado. El desplazamiento constante se verá seguido primero por los términos AR, mientras que los términos MA siempre aparecerán al final.

class CArima:public PowellsMethod
  {
private:
   bool              m_const,m_istrained;
   uint              m_diff_order,m_ar_order,m_ma_order;
   uint              m_arlags[],m_malags[];
   double            m_model[],m_sse;
   double            m_differenced[],m_innovation[],m_leads[];

   void              difference(const uint difference_degree, double &data[], double &differenced[], double &leads[]);
   void              integrate(double &differenced[], double &leads[], double &integrated[]);
   virtual double    func(const double &p[]);


public :
                     CArima(void);
                     CArima(const uint p,const uint d, const uint q,bool use_const_term=true);
                    ~CArima(void);

   uint              GetMaxArLag(void)    { if(m_ar_order) return m_arlags[ArrayMaximum(m_arlags)]; else return 0;}
   uint              GetMinArLag(void)    { if(m_ar_order) return m_arlags[ArrayMinimum(m_arlags)]; else return 0;}
   uint              GetMaxMaLag(void)    { if(m_ma_order) return m_malags[ArrayMaximum(m_malags)]; else return 0;}
   uint              GetMinMaLag(void)    { if(m_ma_order) return m_malags[ArrayMinimum(m_malags)]; else return 0;}
   uint              GetArOrder(void)     { return m_ar_order;  }
   uint              GetMaOrder(void)     { return m_ma_order;  }
   uint              GetDiffOrder(void)   { return m_diff_order;}
   bool              IsTrained(void)      { return m_istrained; }
   double            GetSSE(void)         { return m_sse;      }
   uint              GetArLagAt(const uint shift);
   uint              GetMaLagAt(const uint shift);


   bool              SetARLags(uint &ar_lags[]);
   bool              SetMALags(uint &ma_lags[]);
   bool              Fit(double &input_series[]);
   bool              Fit(double &input_series[],const uint p,const uint d, const uint q,bool use_const_term=true);
   string            Summary(void);
   void              GetModelParameters(double &out_array[]) { ArrayCopy(out_array,m_model);      }
   void              GetModelInnovation(double &out_array[]) { ArrayCopy(out_array,m_innovation); }

  };

GetModelInnovation() escribe en su único argumento de array los valores de error calculados con coeficientes optimizados después del ajuste del modelo. Mientras que la función Summary() retorna una descripción de cadena que detalla el modelo completo, GetArOrder(), GetMaOrder() y GetDiffOrder() retornan el número de términos AR y MA, y el grado de diferenciación del modelo.

GetArLagAt() y GetMaLagAt() toman un argumento entero sin signo que se corresponde con el número de índice del componente AR o MA. Un desplazamiento igual a cero se referirá al primer componente. GetSSE() retorna la suma de los errores cuadráticos del modelo entrenado. IsTrained() retorna true o false dependiendo de si el modelo especificado ha sido entrenado o no.

Como CArima hereda de PowellsMethod, se pueden ajustar varios parámetros del algoritmo de Powell. Encontrará más información sobre PowellsMethod aquí.

Usando la clase CARima

El código del script más abajo muestra cómo se puede construir un modelo y evaluar sus parámetros para una serie determinista. La demostración en el script generará una serie determinista con la opción de indicar un valor de desplazamiento constante y añadir un componente aleatorio para simular el ruido.

El script incluye Arima.mqh y llena el array de entrada con una fila construida a partir de un componente determinista y aleatorio.

#include<Arima.mqh>

input bool Add_Noise=false;
input double Const_Offset=0.625;

Luego declararemos un objeto CArima que defina el modelo AR(2) puro. El método Fit() se llamará con el array de entrada y los resultados del entrenamiento se mostrarán usando la función Summary(). El resultado del script se muestra más abajo.

double inputs[300];
   ArrayInitialize(inputs,0);

   int error_code;

   for(int i=2; i<ArraySize(inputs); i++)
     {
      inputs[i]= Const_Offset;
      inputs[i]+= 0.5*inputs[i-1] - 0.3*inputs[i-2];
      inputs[i]+=(Add_Noise)?MathRandomNormal(0,1,error_code):0;
     }

   CArima arima(2,0,0,Const_Offset!=0);

   if(arima.Fit(inputs))
      Print(arima.Summary());

El script se ejecuta dos veces con y sin el componente de ruido. En la primera ejecución, vemos que el algoritmo ha logrado estimar los coeficientes exactos de la serie. En la segunda ejecución con ruido añadido, el algoritmo ha hecho un buen trabajo al reproducir el verdadero desplazamiento constante y los coeficientes que definen nuestra serie.

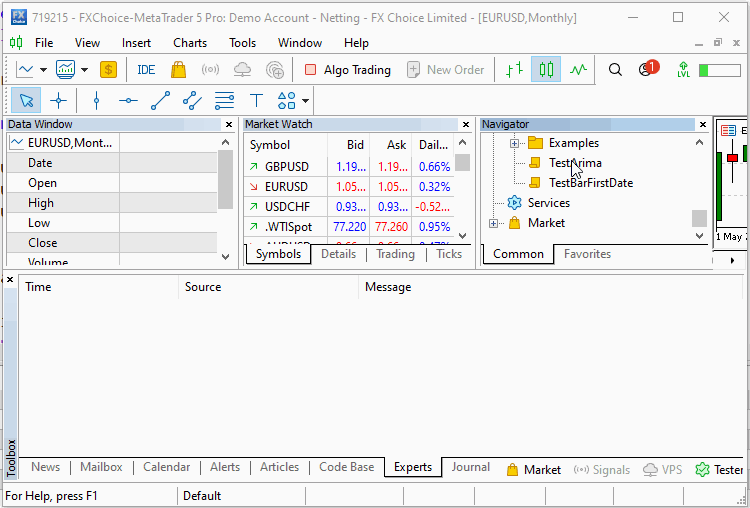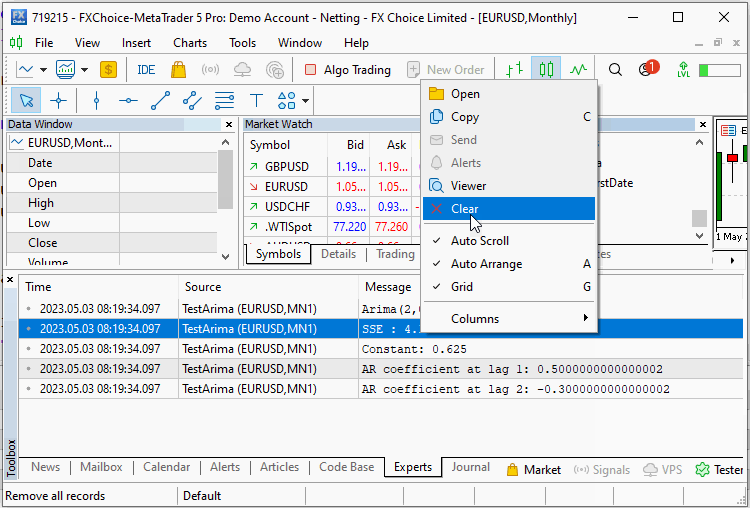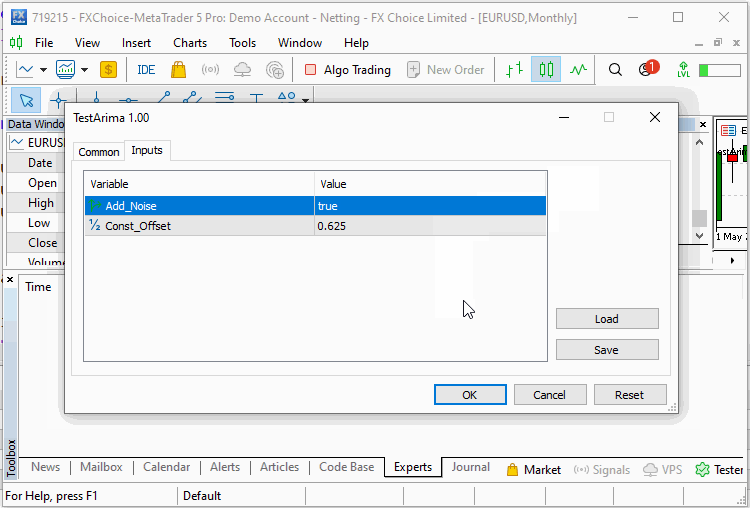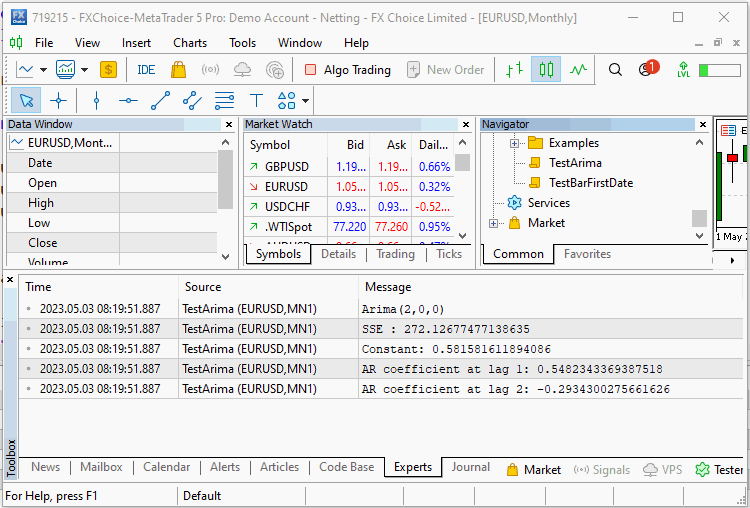
El ejemplo mostrado claramente no resulta similar al tipo de análisis que encontraremos en el mundo real. El ruido añadido a la serie ha resultado modesto en comparación con el ruido encontrado en las series temporales financieras.

Desarrollo de modelos ARIMA

Hasta ahora, hemos considerado la implementación del algoritmo de aprendizaje autorregresivo sin especificar cómo obtener o seleccionar el orden apropiado para el modelo. La formación de modelos es probablemente la parte más fácil del trabajo, a diferencia de la definición de un buen modelo.

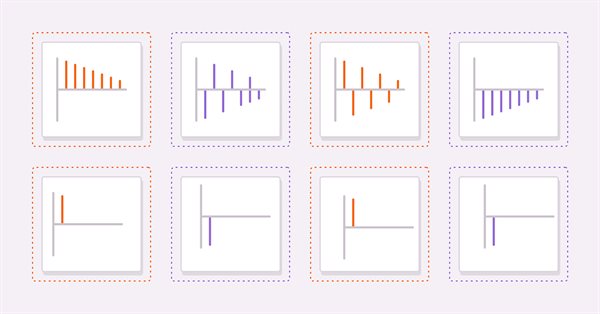
Dos herramientas útiles para la obtención de un modelo adecuado son el cálculo de la autocorrelación y la autocorrelación parcial de la serie estudiada. Veamos cuatro series hipotéticas para ayudar a los lectores a interpretar los gráficos de autocorrelación y autocorrelación parcial.
                                                                  y(t) = AR1* y(t-1) + E(t) (3) 

                 
                                                                  y(t) = E(t) - AR1 * y(t-1) (4) 

            
                                                                  y(t) = MA1 * E(t-1) + E(t) (5) 

                
                                                                   y(t) = E(t) - MA1 * E(t-1) (6) 

    
(3) y (4) son procesos AR(1) puros con coeficientes positivos y negativos, respectivamente. (5) y (6) son procesos MA(1) puros con coeficientes positivos y negativos, respectivamente.  

Las imágenes de arriba muestran las autocorrelaciones (3) y (4), respectivamente. En ambos gráficos, los valores de correlación se vuelven más pequeños a medida que aumenta el retardo. Esto tiene sentido porque el efecto del valor anterior sobre el valor actual disminuirá a medida que se avance en la serie.

Las siguientes figuras muestran gráficos de autocorrelación parcial para el mismo par de series: podemos ver que los valores de correlación se recortan después del primer desfase. Estas observaciones ofrecen la base para formar una regla general sobre los modelos AR. En general, si las autocorrelaciones parciales se rompen más allá de un cierto retraso y simultáneamente comienzan a decaer más allá del mismo retraso, entonces la serie se podrá modelar mediante un modelo AR puro hasta el retraso límite observado en el gráfico de autocorrelación parcial.

 Como podemos ver, los gráficos son idénticos a las autocorrelaciones parciales AR(1).

En general, si todas las autocorrelaciones más allá de un pico o valle en particular son iguales a cero, mientras que las autocorrelaciones parciales se vuelven más pequeñas a medida que se seleccionan más retrasos, entonces la serie podrá ser determinada por el componente MA con el retraso límite observado en el gráfico de autocorrelación.

 
Otras formas de determinar los parámetros p y q del modelo incluyen:

• Criterios de información: existen varios criterios de información, como el Criterio de información de Akaike (AIC) y el Criterio de información bayesiano (BIC), que se puede utilizar para comparar diferentes modelos de ARIMA y elegir el mejor.

• La búsqueda según la cuadrícula implica ajustar diferentes modelos ARIMA con diferentes órdenes en el mismo conjunto de datos y comparar su rendimiento. El orden que ofrece mejores resultados se elige como orden ARIMA óptimo.

• La validación cruzada de series temporales implica dividir los datos de la serie temporal en conjuntos de entrenamiento y de prueba, ajustar los diferentes modelos ARIMA al conjunto de entrenamiento y evaluar su desempeño en el conjunto de prueba. El orden ARIMA que ofrece el mejor error de prueba se elige como orden óptimo.

Debemos tener en cuenta que no existe un enfoque único para elegir un orden ARIMA, y que encontrar el mejor orden para una serie temporal particular puede requerir de pruebas y errores, así como de un buen conocimiento del dominio de estudio.

Conclusión

Hoy hemos mostrado una clase CArima que encapsula un algoritmo de aprendizaje autorregresivo usando el método de minimización de Powell. El código completo de la clase se incluye en el archivo zip que verá a continuación, junto con un script que demuestra su uso.

Archivo	Descripción
Arima.mqh	archivo include con la definición de la clase CArima
PowellsMethod.mqh	archivo include con la definición de la clase PowellsMethod
TestArima	Script que muestra el uso de la clase CArima para analizar una serie parcialmente determinista.