Indicadores alternativos de riesgo y rentabilidad en MQL5

Introducción

Todos los tráders intentan maximizar el porcentaje de rentabilidad de sus inversiones, pero una mayor rentabilidad suele conllevar un mayor riesgo. Por este motivo, una rentabilidad ajustada al riesgo será la principal medida de rentabilidad en el sector de la inversión. Existen muchas medidas diferentes de rentabilidad ajustada al riesgo, cada una con sus propias ventajas e inconvenientes. El ratio de Sharpe es una medida popular de riesgo y rentabilidad conocida por imponer condiciones previas poco realistas a la distribución de la rentabilidad analizada. Esto ha llevado inevitablemente al desarrollo de medidas de rendimiento alternativas sin las desventajas que conlleva el ratio de Sharpe. En este artículo, consideraremos la aplicación de medidas alternativas de riesgo y rentabilidad y generaremos curvas de capital hipotéticas para analizar sus características.

Modelización de la curva de equidad

Para garantizar la interpretabilidad, usaremos los datos del SP500 como base de la estrategia comercial modelada. No utilizaremos ninguna regla comercial específica, sino que utilizaremos números aleatorios para crear las curvas de capital y las series de rentabilidad correspondientes. El capital inicial se estandarizará a una cantidad ajustable. Los números aleatorios se definirán usando un número inicial (seed) para que cualquiera pueda reproducir los experimentos, si así lo desea.

Visualización de las curvas de equidad

La siguiente figura muestra una aplicación MetaTrader 5 (MT5) implementada como un asesor que muestra tres curvas de equidad. La curva de equidad roja será la referencia en la que se basen las curvas de equidad azul y verde. El valor de referencia podrá modificarse ajustando el capital inicial. Se ajustará desde la aplicación.  

Las curvas de equidad se construirán a partir de las series de referencia. Cada una estará definida por un componente aleatorio que podrá controlarse mediante dos constantes ajustables, el coeficiente de media y el coeficiente de desviación típica. Combinados con la desviación típica de la rentabilidad del índice de referencia, definirán los parámetros de los números aleatorios distribuidos normalmente utilizados para crear las dos curvas hipotéticas de equidad.   

En primer lugar, calcularemos las rentabilidades utilizando los precios de cierre diarios del SP500 para el periodo comprendido entre el 20 de marzo de 2020 y el 5 de enero de 2022, ambos inclusive. La curva de equidad se construirá a partir de una serie de rentabilidades. Usando las series que definen el capital y la rentabilidad, compararemos el rendimiento calculado considerando el aspecto de esta curva de equidad.

El código de la aplicación se adjuntará al artículo.

Coeficientes de reducción

La reducción es la mayor cantidad de dinero perdida por una estrategia entre dos momentos cualesquiera. Este valor ofrece una indicación del riesgo que ha asumido la estrategia para alcanzar sus objetivos, si es que ha asumido alguno. Cuando calculamos y agregamos una serie formada por un número aleatorio de las mayores reducciones, el resultado puede utilizarse como medida de variabilidad.

Coeficiente de Burke

En 1994, Burke escribió un artículo titulado "A Sharper Ratio" en el que presentaba el Ratio de Burke como una alternativa al popular Ratio de Sharpe. El ratio de Burke sustituye el denominador de la fórmula del ratio de Sharpe por el cuadrado de la suma del valor definido de las mayores reducciones absolutas. El numerador puede ser la rentabilidad media o la rentabilidad absoluta en efectivo de la estrategia/portafolio, es decir, la rentabilidad neta. Consideraremos las dos variantes del cálculo. Distinguiremos dos versiones: el ratio de Burke basado en el beneficio neto y el ratio de Burke de las rentabilidades medias. Las fórmulas serán las siguientes.

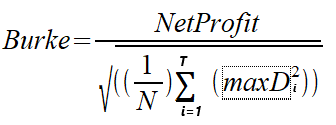
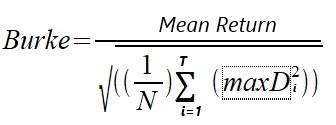
MaxD es una serie de las mayores reducciones T absolutas calculadas a partir de valores de equidad. N representa el número de valores patrimoniales usados en los cálculos.

El ratio de beneficio neto Burke se implementa como netprofit_burke(). La función requiere un array de valores de capital que describa la curva de capital y un valor entero que indique el número de mayores reducciones que deben incluirse en el cálculo.

//+------------------------------------------------------------------+
//|Net profit based Burke ratio                                      |
//+------------------------------------------------------------------+
double netprofit_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
        {
         sumdd+=(outdd[i]*outdd[i]);
        }
      return (in_ec[insize-1]-in_ec[0])/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Si especificamos un valor por defecto de cero, la función utilizará la fórmula N/20 para establecer el número de reducciones que deben tenerse en cuenta, siendo N el tamaño del array de fondos.

La función MaxNDradowns() se conectará para recoger el número especificado de reducciones. Genera una serie de las mayores reducciones absolutas, ordenadas de forma ascendente.

//+------------------------------------------------------------------+
//|Maximum drawdowns function given equity curve                     |
//+------------------------------------------------------------------+
bool MaxNDrawdowns(const int num_drawdowns,double &in_ec[],double &out_dd[])
  {
   ZeroMemory(out_dd);

   ResetLastError();

   if(num_drawdowns<=0)
     {
      Print("Invalid function parameter for num_drawdowns ");
      return false;
     }
   double u[],v[];

   int size = ArraySize(in_ec);

   if((ArrayResize(v,(size*(size-1))/2)< int((size*(size-1))/2))||
      (ArraySize(out_dd)!=num_drawdowns && ArrayResize(out_dd,num_drawdowns)<num_drawdowns))
     {
      Print(__FUNCTION__, " resize error ", GetLastError());
      return false;
     }

   int k=0;
   for(int i=0; i<size-1; i++)
     {
      for(int j=i+1; j<size; j++)
        {
         v[k]=in_ec[i]-in_ec[j];
         k++;
        }
     }

   ArraySort(v);

   for(int i=0; i<k; i++)
     {
      if(v[i]>0)
        {
         if(i)
           {
            if(!ArrayRemove(v,0,i))
              {
               Print(__FUNCTION__, " error , ArrayRemove: ",GetLastError());
               return false;
              }
            else
               break;
           }
         else
            break;
        }
     }

   size=ArraySize(v);

   if(size && size<=num_drawdowns)
     {
      if(ArrayCopy(out_dd,v)<size)
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      else
         return (true);
     }


   if(ArrayCopy(out_dd,v,0,size-num_drawdowns,num_drawdowns)<num_drawdowns)
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return false;
     }


   return(true);

  }

El cálculo del coeficiente de Burke, que utiliza la rentabilidad media como numerador, se implementa como una función meanreturns_burke y tiene parámetros de entrada similares.

//+------------------------------------------------------------------+
//|Mean return based Burke ratio                                     |
//+------------------------------------------------------------------+
double meanreturns_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double rets[];

   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(ArrayResize(rets,insize-1)<insize-1)
     {
      Print(__FUNCTION__," Memory allocation error ",GetLastError());
      return 0;
     }

   for(int i=1; i<insize; i++)
      rets[i-1] = (in_ec[i]/in_ec[i-1]) - 1.0;

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
         sumdd+=(outdd[i]*outdd[i]);
      return MathMean(rets)/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Relación entre el beneficio neto y la reducción máxima

La fórmula del Ratio Burke, que usa el beneficio neto como numerador, es similar al Ratio Beneficio Neto/Reducción Máxima (Netprofit to Maximum Drawdown ratio, NPMD). La diferencia estriba en el uso de la mayor reducción para calcular el coeficiente NPMD.

El cálculo NPMD se implementará como una función netProfiMaxDD(), que requerirá un array de valores de equidad como datos de entrada.

//+------------------------------------------------------------------+
//|Net profit to maximum drawdown ratio                              |
//+------------------------------------------------------------------+
double netProfiMaxDD(double &in_ec[])
  {
   double outdd[];
   int insize=ArraySize(in_ec);

   if(MaxNDrawdowns(1,in_ec,outdd))
      return ((in_ec[insize-1]-in_ec[0])/outdd[0]);
   else
      return 0;
  }

Los ratios basados en la reducción se introdujeron para abordar algunas de las críticas al ratio de Sharpe. Los cálculos no penalizan los beneficios anormales o elevados y, lo que es más importante, no son paramétricos. El uso de reducciones absolutas en el denominador, aunque suponga una ventaja, hace que los coeficientes Burke y NPMD favorezcan las estrategias con saltos a la baja relativamente pequeños.

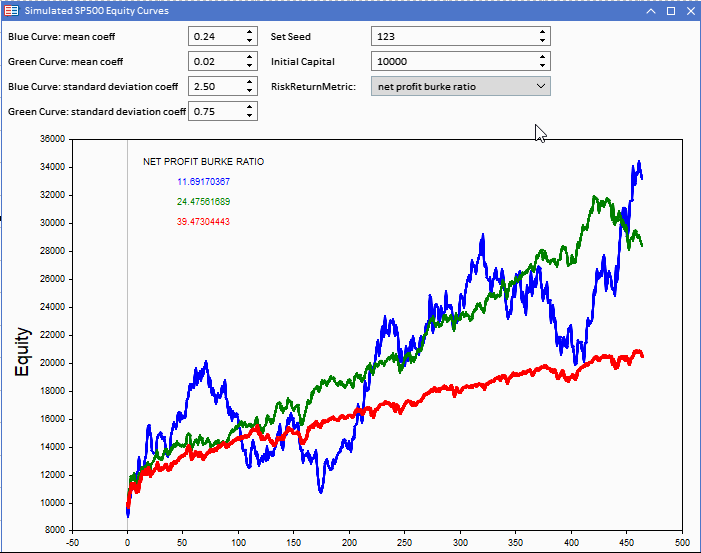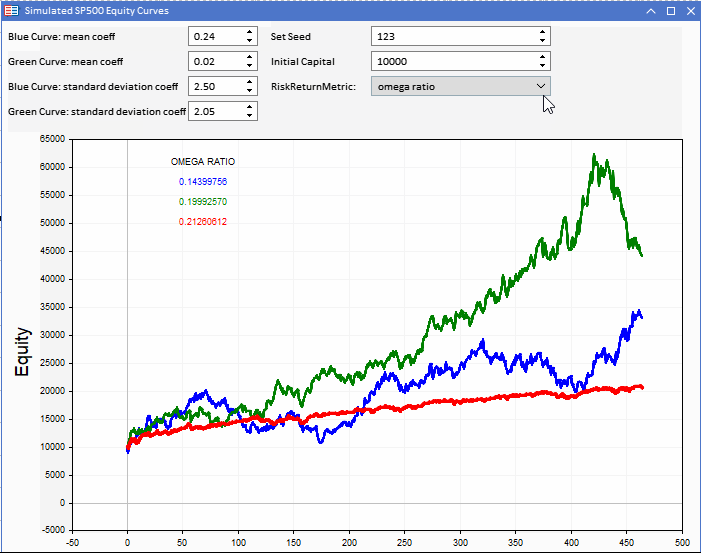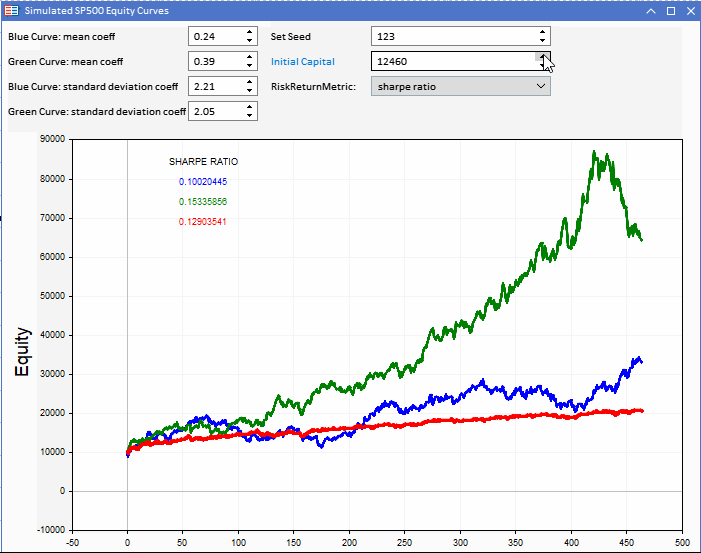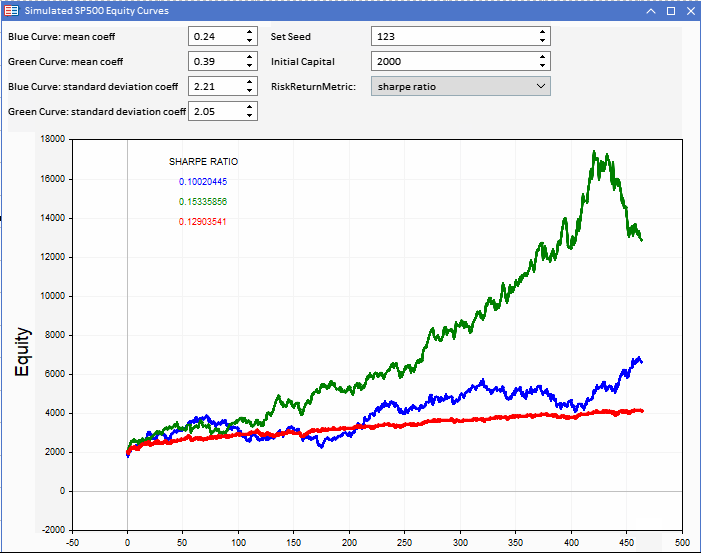
En referencia a la herramienta de visualización de la curva de equidad: la curva azul tiene la rentabilidad más alta, pero su puntuación es inferior a las demás.

Los valores de referencia de ambos coeficientes ponen de relieve lo engañosos que pueden resultar los indicadores cuando se utilizan para comparar la eficacia de las estrategias. Los ratios subyacentes son mucho más elevados, aunque las otras curvas arrojan rentabilidades reales más altas.

El uso de las reducciones absolutas puede sobrestimar el riesgo en comparación con el uso de una distribución de rentabilidades negativas, como en el caso del ratio de Sharpe.

Comparando los valores de Sharpe, podemos ver que la curva verde tiene la puntuación más alta con una diferencia mucho menor entre los resultados de la estrategia modelada.

Interpretación de los coeficientes de reducción

Cuanto mayor sea el coeficiente de Burke o NPMD, mejor será el rendimiento ajustado al riesgo de la estrategia de inversión. Esto significa que la estrategia generará un mayor beneficio en comparación con el riesgo asumido.

- Si el coeficiente Burke o NPMD es superior a 0, indicará que la estrategia de inversión proporciona rentabilidades superiores al riesgo estimado.

- Si el ratio Burke o NPMD es inferior a 0, indicará que la estrategia de inversión no está generando un exceso de beneficios suficiente en relación con el riesgo asumido.

Indicadores de momentos parciales

Los ratios basados en el momento parcial son otro intento de crear una alternativa al ratio de Sharpe. Se basan en el concepto estadístico de semidispersión y proporcionan una indicación de la rentabilidad de una estrategia en términos de riesgo a la baja (rentabilidades negativas) frente al potencial al alza (rentabilidades positivas). Para calcular los indicadores de momentos parciales, primero deberemos determinar el beneficio parcial y la pérdida parcial. Estos valores se obtienen determinando una rentabilidad umbral, generalmente la rentabilidad mínima aceptable o la tasa sin riesgo, y luego calculando la diferencia entre la rentabilidad real y la rentabilidad umbral para cada observación.

Las diferencias que se encuentren por encima del umbral del momento parcial inferior o por debajo del umbral del momento parcial superior (HPM) podrán ignorarse en el cálculo. El momento parcial inferior (MPI) mide la desviación cuadrática de las rentabilidades que caen por debajo de un umbral, mientras que el momento parcial superior (MPS) mide la desviación cuadrática de las rentabilidades que superan el umbral. Los momentos parciales presentan una visión alternativa de los ratios de riesgo y reducción de pérdidas, centrándose en el riesgo asociado a las rentabilidades que están por debajo o por encima de un determinado umbral.

A continuación le presentamos las fórmulas para LPM y HPM, respectivamente:

Donde thresh es el umbral, x es la rentabilidad observada, y max define el valor máximo entre la diferencia resultante y cero antes de ser elevado a grado n. n definirá el grado de impulso parcial. En n=0, LPM se convierte en la probabilidad de que la observación sea inferior al umbral y HPM da la probabilidad de que resulte superior. N será el número de ingresos observados. Consideraremos dos coeficientes de momentos parciales, el Omega generalizado y el Coeficiente de Potencial de Crecimiento (UPR).

Omega

El omega generalizado se define usando un único término en n grados y un valor umbral que define el LPM utilizado en el cálculo.

La función omega() implementará el cálculo del coeficiente Omega, tomando como entrada un array de valores de retorno. La función usa el momento parcial inferior al cuadrado, suponiendo que el umbral de retorno sea cero.

//+------------------------------------------------------------------+
//|omega ratio                                                       |
//+------------------------------------------------------------------+
double omega(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);

   if(pmomentl)
      return MathMean(rt)/pmomentl;
   else
      return 0;
  }

Potencial de crecimiento

La UPR utiliza dos términos de grado n (n1 y n2 en la fórmula) y un valor umbral. n1 define el grado de HPM en el numerador, mientras que n2 define el grado de LPM en el denominador.

De manera similar a la implementación de Omega de la métrica de rendimiento, upsidePotentialRatio() calculará el coeficiente UPR. El cálculo también utilizará momentos parciales al cuadrado, y los umbrales se retornarán como cero.

//+------------------------------------------------------------------+
//|Upside potential ratio                                            |
//+------------------------------------------------------------------+
double upsidePotentialRatio(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentu=MathPow(partialmoment(2,rt,rb,true),0.5);
   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);
   if(pmomentl)
      return pmomentu/pmomentl;
   else
      return 0;
  }

Los cálculos de momentos parciales se implementarán en la función partsmoment(). Los datos de entrada requeridos serán el grado de momento como un entero sin signo, dos arrays de tipo double y un valor lógico. El primer array deberá contener la rentabilidad observada mientras que el segundo contendrá el umbral o la rentabilidad de referencia utilizada en los cálculos. El valor lógico determinará el tipo de momento parcial a calcular: true para un momento parcial alto y false para un momento parcial bajo.

//+------------------------------------------------------------------+
//|Partial Moments                                                   |
//+------------------------------------------------------------------+
double partialmoment(const uint n,double &rt[],double &rtb[],bool upper=false)
  {
   double pm[];
   int insize=ArraySize(rt);

   if(n)
     {
      if(ArrayResize(pm,insize)<insize)
        {
         Print(__FUNCTION__," resize error ", GetLastError());
         return 0;
        }

      for(int i=0; i<insize; i++)
         pm[i] = (!upper)?MathPow(MathMax(rtb[i]-rt[i],0),n):MathPow(MathMax(rt[i]-rtb[i],0),n);
      return MathMean(pm);
     }
   else
     {
      int k=0;
      for(int i=0; i<insize; i++)
        {
         if((!upper && rtb[i]>=rt[i]) || (upper && rt[i]>rtb[i]))
           {
            ArrayResize(pm,k+1,1);
            pm[k]=rt[i];
            ++k;
           }
         else
            continue;
        }

      return MathMean(pm);

     }

  }

Observando los ratios Omega y UPR de nuestras curvas de equidad, notaremos la similitud del rating con el ratio Sharpe.

Una vez más, la coherencia resultará preferible a unas curvas de equidad más volátiles. Omega parece definitivamente una alternativa viable al ratio de Sharpe.

Interpretación de la relación de momentos parciales

La interpretación de Omega es mucho más sencilla que la de UPR. Cuanto más alto sea omega, mejor. Los valores negativos indicarán estrategias poco rentables, mientras que los positivos sugerirán rentabilidades superiores al nivel de riesgo.

Por otra parte, el UPR puede parecer un poco extraño a la hora de interpretarlo. Echemos ahora un vistazo a algunos modelos de curvas de equidad con perfiles de rendimiento divergentes.

La curva azul de la equidad muestra una rentabilidad negativa, pero el resultado del EPU es positivo. Aún más extraños son los resultados de las curvas de equidad verde y roja. Las curvas en sí son casi similares: la curva de capital verde ofrece una mayor rentabilidad, pero el valor UPR es menor que el de la curva roja.

Análisis de regresión de la rentabilidad - Alfa de Jensen

La regresión lineal permite construir la línea que mejor se ajuste a un conjunto de datos. Así, los indicadores basados en la regresión medirán la linealidad de las curvas de capital. El alfa de Jensen calculará el valor de alfa en la ecuación de regresión estándar. Así, cuantificará la relación entre la rentabilidad de referencia y la observada.

Para calcular el valor de alfa, podremos utilizar el método de los mínimos cuadrados. La función leastsquarefit() tomará como entrada dos arrays que definirán una respuesta y un predictor. En este contexto, la respuesta sería un array con las rentabilidades observadas, mientras que el predictor sería un array de rentabilidades de referencia. La función emitirá valores alfa y beta, cuyas referencias deberán proporcionarse cuando se llame a la función.

//+------------------------------------------------------------------+
//|linear model using least squares fit y=a+bx                       |
//+------------------------------------------------------------------+
double leastsquaresfit(double &y[],double &x[], double &alpha,double &beta)
  {
   double esquared=0;

   int ysize=ArraySize(y);
   int xsize=ArraySize(x);

   double sumx=0,sumy=0,sumx2=0,sumxy=0;

   int insize=MathMin(ysize,xsize);

   for(int i=0; i<insize; i++)
     {
      sumx+=x[i];
      sumx2+=x[i]*x[i];
      sumy+=y[i];
      sumxy+=x[i]*y[i];
     }

   beta=((insize*sumxy)-(sumx*sumy))/((insize*sumx2)-(sumx*sumx));
   alpha=(sumy-(beta*sumx))/insize;

   double pred,error;

   for(int i=0; i<insize; i++)
     {
      pred=alpha+(beta*x[i]);
      error=pred-y[i];
      esquared+=(error*error);
     }

   return esquared;

  }

Aplicando el Alfa de Jensen a nuestras curvas de equidad modeladas, obtendremos una medida de la linealidad de las curvas de equidad verde y azul en relación con la referencia (curva de equidad roja).

Este será el primer indicador que evaluará la curva azul de la equidad como la estrategia más eficaz. Esta métrica suele recompensar el buen rendimiento cuando los resultados de las métricas de referencia son malos. El Alfa de Jensen puede indicar una rentabilidad positiva aunque la rentabilidad absoluta sea negativa. Esto puede ocurrir cuando las rentabilidades absolutas del índice de referencia son simplemente peores que las rentabilidades estudiadas. Por ello, tenga cuidado al utilizar este indicador.

Interpretación del Alpha de Jensen

Si el Alfa de Jensen es positivo, indica que el portafolio/estrategia ha proporcionado rentabilidades superiores al índice de referencia, lo que indica una rentabilidad superior tras considerar el nivel de riesgo. Si el alfa de Jensen es negativo, significará que la estrategia ha obtenido peores resultados que el índice de referencia.

Además del valor alfa, el valor beta obtenido por el método de los mínimos cuadrados proporciona una medida de la sensibilidad de las rentabilidades en relación con el índice de referencia. Una beta igual a 1 indicará que las rentabilidades de la estrategia cambian en sincronía con el índice de referencia. Una beta inferior a 1 indicará que la curva de equidad es menos volátil que la curva de referencia, mientras que una beta superior a 1 indicará una mayor volatilidad.

Conclusión

Hemos descrito la aplicación de varias medidas de rentabilidad ajustadas al riesgo que pueden utilizarse como alternativas al ratio de Sharpe. En mi opinión, el mejor candidato es el indicador omega. Ofrece las mismas ventajas que el ratio de Sharpe sin ninguna expectativa de normalidad de la distribución de los ingresos. No obstante, también hay que tener en cuenta que es mejor considerar múltiples medidas de rendimiento de la estrategia a la hora de tomar decisiones de inversión. Ninguna métrica por sí misma puede dar una imagen completa del riesgo o la rentabilidad esperados. Recuerde también que la mayoría de las medidas de rentabilidad del riesgo son medidas retrospectivas, y que los resultados pasados no garantizan ningún resultado futuro. Por consiguiente, es importante considerar otros factores como los objetivos de inversión, el horizonte temporal y la tolerancia al riesgo a la hora de evaluar las opciones de inversión.

El código fuente de todas las métricas se encuentra en PerformanceRatios.mqh. Cabe señalar que ninguna de las implementaciones arroja cifras anuales. El archivo zip adjunto contiene también el código de la aplicación utilizada para visualizar nuestras curvas de capital modeladas. La aplicación se implementará utilizando la biblioteca EasyAndFastGUI disponible en CodeBase en mql5.com. Adjuntamos al artículo el código fuente del asesor y una versión compilada operativa.

Nombre del archivo	Descripción
Mql5\Files\sp500close.csv	Archivo CSV con los precios de cierre del SP500 utilizados en el cálculo de las curvas de equidad
Mql5\Include\PerformanceRatios.mqh	Archivo de inclusión con las definiciones de todas las métricas de rendimiento descritas en el artículo
Mql5\Experts\EquityCurves.mq5	Código fuente del asesor para la herramienta de visualización. Su compilación requiere una GUI sencilla y rápida disponible en CodeBase
Mql5\Experts\EquityCurves.ext	Versión compilada del asesor