Реализация алгоритма обучения ARIMA на MQL5

Введение

Большинство форекс- и криптотрейдеров, стремящихся использовать краткосрочные движения, страдают от нехватки фундаментальной информации. В этом случае им могут помочь стандартные методы временных рядов. Джордж Бокс и Гвилим Дженкинс разработали, пожалуй, самый популярный метод прогнозирования временных рядов. Несмотря на то, что со временем в метод вносились улучшения, его основные принципы по-прежнему актуальны и сегодня.

Одним из производных метода является авторегрессионная интегрированная скользящая средняя (Autoregressive Integrated Moving Average, ARIMA), которая стала популярным методом прогнозирования временных рядов. Это класс моделей, который фиксирует временные зависимости в ряде данных и обеспечивает основу для моделирования нестационарных временных рядов. В этой статье мы возьмем метод минимизации функций Пауэллса в качестве основы для создания обучающего алгоритма ARIMA с использованием языка программирования MQL5.

Обзор ARIMA

Бокс и Дженкинс утверждали, что большинство временных рядов можно смоделировать с помощью одной или обеих из двух структур. Одной из них является авторегрессия (AR), что означает, что значение ряда можно объяснить по отношению к его предыдущим значениям вместе с постоянным смещением и небольшой разницей, обычно называемой инновацией, или шумом. Обратите внимание, что в этом тексте мы будем называть компонент шума или ошибки инновацией. Нововведение объясняет случайную вариацию, которую невозможно объяснить другими способами.

Второй структурой, лежащей в основе модели ARIMA, является скользящая средняя (MA). Эта модель утверждает, что значение ряда представляет собой пропорциональную сумму определенного количества предыдущих условий инновации, текущей инновации и, опять же, постоянного смещения. Существует множество других статистических условий, определяющих эти модели, но мы не будем вдаваться в подробности. В Интернете можно найти много необходимой информации, но мы больше заинтересованы в ее применении.

Мы не ограничиваемся только чистыми моделями MA и AR, мы можем комбинировать их для создания смешанных моделей, называемых моделями авторегрессионной скользящей средней (Autoregressive Moving Average, ARMA). В модели ARMA мы указываем конечное число запаздывающих рядов и составляющих шума (noise terms) в дополнение к постоянному смещению и текущей составляющей инновации (innovation term).

Одно из фундаментальных требований, которое влияет на применение всех этих структур, заключается в том, что моделируемый ряд должен быть стационарным. В зависимости от того, насколько строгое определение стационарности вам удобно, модели, описанные до сих пор, технически непригодны для применения с финансовыми временными рядами. Здесь на помощь приходит ARIMA. Математическое интегрирование противоположно дифференцированию. Когда нестационарный временной ряд дифференцируется один или несколько раз, результирующий ряд обычно имеет лучшую стационарность. При первом дифференцировании ряда становится возможным применить эти модели к результирующему ряду. Буква I в аббревиатуре ARIMA относится к необходимости интегрировать (Integrate) примененное дифференцирование, чтобы вернуть смоделированный ряд в исходную область.

Описание авторегрессионной модели

Существует стандартное описание модели. Количество составляющих AR (не считая постоянной составляющей) обычно называют p. Составляющие MA обозначаются как q, а d описывает, сколько раз исходный ряд был дифференцирован. Используя эти термины, модель ARIMA определяется как ARIMA (p, d, q). Чистые процессы можно изобразить как MA(q) и AR(p). Смешанные модели без различий записываются как ARMA(p,q). Это обозначение предполагает, что составляющие являются смежными. Например, ARMA(4,2) означает, что серия может быть описана 4 последовательными составляющими AR и двумя предыдущими последовательными составляющими инновации. Используя ARIMA, мы можем изобразить чистые процессы, указав p, q или d равными нулю. Например, ARIMA(1,0,0) сводится к чистой модели AR(1).

Большинстве авторегрессионных моделей указывают, что соответствующие составляющие являются непрерывными, от отставания 1 до отставания p и отставания q для терминов AR и MA соответственно. Алгоритм, который будет продемонстрирован, позволит указать несмежные запаздывания для составляющих MA и/или AR. Еще одна гибкость, которую привнесет алгоритм, — это возможность указывать модели с постоянным смещением или без него.

Например, можно будет построить модели, определенные функцией ниже:
                                 

                                                        y(t) = AR1* y(t-4) + AR2*y(t-6) + E(t)         (1)

Приведенная выше функция описывает чистый процесс AR(2) без постоянного смещения с текущим значением, определяемым значениями серии 4 и 6 предыдущих временных интервалов назад. Стандартное описание не дает способа специфицировать такую модель, но нас не должны сдерживать такие ограничения.
 

Расчет коэффициентов модели и постоянного смещения

Модель может иметь коэффициенты p+q, которые необходимо рассчитать. Для этого мы используем спецификацию модели для прогнозирования известных значений ряда, затем сравниваем прогнозируемые значения с известными значениями и вычисляем сумму квадратов ошибок. Оптимальными будут те коэффициенты, которые дают наименьшую сумму квадратов ошибок.

При прогнозировании следует соблюдать осторожность из-за ограничений, налагаемых недоступностью данных, простирающихся до бесконечности. Если в спецификации модели есть какие-либо составляющие AR, мы можем начать делать прогнозы только после того количества значений, которое соответствует наибольшему отставанию всех составляющих AR.

Используя пример, указанный выше (1), мы сможем начать делать прогнозы только с временного интервала 7, поскольку любые предыдущие прогнозы будут ссылаться на неизвестные значения до начала серии.

Следует отметить, что если бы (1) имел какие-либо составляющие MA, то в этот момент модель рассматривалась бы как чисто авторегрессионная, поскольку у нас еще нет ряда инноваций. Ряд значений инноваций будет формироваться по мере того, как будут делаться прогнозы на будущее. Возвращаясь к примеру, первый прогноз в седьмом временном интервале будет рассчитываться с произвольными начальными коэффициентами AR.

 Разница между рассчитанным прогнозом и известным значением в седьмом временном интервале будет инновацией для этого интервала. Если указаны какие-либо составляющие MA, они будут включены в расчет прогноза по мере того, как станут известны соответствующие запаздывающие значения инноваций. В противном случае составляющие MA просто обнуляются. В случае чистой модели MA выполняется аналогичная процедура, за исключением того, что на этот раз, если необходимо включить постоянное смещение, оно инициализируется как среднее значение ряда.

Описанный метод имеет только одно очевидное ограничение. Известный ряд должен содержать соизмеримое количество значений по отношению к порядку применения модели. Чем больше составляющих и/или чем больше запаздывание этих составляющих, тем больше значений нам нужно, чтобы эффективно соответствовать модели. Процесс обучения завершается применением соответствующего алгоритма глобальной минимизации для оптимизации коэффициентов. Алгоритм, который мы будем использовать для минимизации ошибки предсказания, называется методом Пауэллса. Применяемые здесь особенности реализации описаны в статье "Прогнозирование временных рядов при помощи экспоненциального сглаживания".

Класс CArima

Алгоритм обучения ARIMA будет содержаться в классе CArima в Arima.mqh. В классе есть два конструктора, каждый из которых инициализирует авторегрессионную модель. Конструктор по умолчанию создает чистую модель AR(1) с постоянным смещением.

CArima::CArima(void)
  {
   m_ar_order=1;
//---
   ArrayResize(m_arlags,m_ar_order);
   for(uint i=0; i<m_ar_order; i++)
      m_arlags[i]=i+1;
//---
   m_ma_order=m_diff_order=0;
   m_istrained=false;
   m_const=true;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

Параметризованный конструктор позволяет лучше контролировать определение модели. Он принимает четыре аргумента, перечисленных ниже:

Параметры	Тип параметра	Описание параметра
p	целочисленный беззнаковый	количество составляющих AR для модели
дн.	целочисленный беззнаковый	задает степень различия, применяемую к моделируемому ряду
q	целочисленный беззнаковый	указывает количество составляющих MA, которые должна содержать модель
use_const_term	bool	устанавливает использование постоянного смещения в модели

CArima::CArima(const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }


   m_istrained=false;
   m_const=use_const_term;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

В дополнение к двум предоставленным конструкторам модель также можно указать с помощью одного из перегруженных методов Fit(). Оба метода принимают моделируемый ряд данных в качестве первого аргумента. Один метод Fit() имеет только один аргумент, в то время как второй требует еще четыре аргумента, и все они идентичны тем, которые уже задокументированы в таблице выше.

bool CArima::Fit(double &input_series[])
  {

   uint input_size=ArraySize(input_series);

   uint in = m_ar_order+ (m_ma_order*2);

   if(input_size<=0 || input_size<in)
      return false;

   if(m_diff_order)
      difference(m_diff_order,input_series,m_differenced,m_leads);
   else
      ArrayCopy(m_differenced,input_series);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   double parameters[];
   ArrayResize(parameters,(m_const)?m_ar_order+m_ma_order+1:m_ar_order+m_ma_order);
   ArrayInitialize(parameters,0.0);

   int iterations = Optimize(parameters);

   if(iterations>0)
      m_istrained=true;
   else
      return false;

   m_sse=PowellsMethod::GetFret();

   ArrayCopy(m_model,parameters);

   return true;

  }

Использование метода с большим количеством параметров перезаписывает любую модель, которая была указана ранее, а также предполагает, что запаздывания составляющих находятся рядом друг с другом. Оба предполагают, что ряд данных, указанный в качестве первого параметра, не дифференцирован. Таким образом, дифференциация будет применяться, если она указана в параметрах модели. Оба метода возвращают логическое значение, обозначающее успех или неудачу процесса обучения модели.

bool CArima::Fit(double&input_series[],const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }

   m_istrained=false;
   m_const=use_const_term;

   ZeroMemory(m_innovation);
   ZeroMemory(m_model);
   ZeroMemory(m_differenced);

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);

   return Fit(input_series);

  }

Что касается установки запаздываний для составляющих AR и MA, класс предоставляет методы SetARLags() и SetMALags() соответственно. Оба работают одинаково, принимая один аргумент массива, элементы которого должны быть соответствующими задержками для модели, уже заданной одним из конструкторов. Размер массива должен соответствовать соответствующему порядку составляющих AR или MA. Элементы массива могут содержать любое значение, большее или равное единице. Давайте рассмотрим пример задания модели с несмежными задержками AR и MA.

Модель, которую мы хотим построить, определяется функцией ниже:
         

                                        y(t) = AR1*y(t-2) + AR2*y(t-5) + MA1*E(t-1) + MA2*E(t-3) + E(t)                 (2)

Эта модель определяется процессом ARMA(2,2) с использованием задержек AR, равных 2 и 5, и задержек MA, равных 1 и 3.
В приведенном ниже коде показано, как можно указать такую модель.

CArima arima(2,0,2);

uint alags [2]= {2,5};
uint mlags [2]= {1,3};

if(arima.SetARLags(alags) && arima.SetMALags(mlags))
   Print(arima.Summary());

После успешного подбора модели к ряду данных с помощью одного из методов Fit() оптимальные коэффициенты и постоянное смещение можно получить, вызвав метод GetModelParameters(). Требуется аргумент-массив, в который будут записываться все оптимизированные параметры модели. За постоянным смещением первыми будут следовать составляющие AR, а составляющие MA всегда будут перечисляться последними.

class CArima:public PowellsMethod
  {
private:
   bool              m_const,m_istrained;
   uint              m_diff_order,m_ar_order,m_ma_order;
   uint              m_arlags[],m_malags[];
   double            m_model[],m_sse;
   double            m_differenced[],m_innovation[],m_leads[];

   void              difference(const uint difference_degree, double &data[], double &differenced[], double &leads[]);
   void              integrate(double &differenced[], double &leads[], double &integrated[]);
   virtual double    func(const double &p[]);


public :
                     CArima(void);
                     CArima(const uint p,const uint d, const uint q,bool use_const_term=true);
                    ~CArima(void);

   uint              GetMaxArLag(void)    { if(m_ar_order) return m_arlags[ArrayMaximum(m_arlags)]; else return 0;}
   uint              GetMinArLag(void)    { if(m_ar_order) return m_arlags[ArrayMinimum(m_arlags)]; else return 0;}
   uint              GetMaxMaLag(void)    { if(m_ma_order) return m_malags[ArrayMaximum(m_malags)]; else return 0;}
   uint              GetMinMaLag(void)    { if(m_ma_order) return m_malags[ArrayMinimum(m_malags)]; else return 0;}
   uint              GetArOrder(void)     { return m_ar_order;  }
   uint              GetMaOrder(void)     { return m_ma_order;  }
   uint              GetDiffOrder(void)   { return m_diff_order;}
   bool              IsTrained(void)      { return m_istrained; }
   double            GetSSE(void)         { return m_sse;      }
   uint              GetArLagAt(const uint shift);
   uint              GetMaLagAt(const uint shift);


   bool              SetARLags(uint &ar_lags[]);
   bool              SetMALags(uint &ma_lags[]);
   bool              Fit(double &input_series[]);
   bool              Fit(double &input_series[],const uint p,const uint d, const uint q,bool use_const_term=true);
   string            Summary(void);
   void              GetModelParameters(double &out_array[]) { ArrayCopy(out_array,m_model);      }
   void              GetModelInnovation(double &out_array[]) { ArrayCopy(out_array,m_innovation); }

  };

GetModelInnovation() записывает в свой единственный аргумент-массив значения ошибок, рассчитанные с оптимизированными коэффициентами после подгонки модели. В то время как функция Summary() возвращает строковое описание, в котором подробно описывается полная модель, GetArOrder(), GetMaOrder() и GetDiffOrder() возвращают количество составляющих AR и MA, а также степень дифференциации для модели.

GetArLagAt() и GetMaLagAt() принимают целочисленный беззнаковый аргумент, который соответствует порядковому номеру составляющей AR или MA. Нулевой сдвиг относится к первой составляющей. GetSSE() возвращает сумму квадратов ошибок для обученной модели. IsTrained() возвращает true или false в зависимости от того, была ли обучена указанная модель или нет.

Поскольку CArima наследуется от PowellsMethod, можно настраивать различные параметры алгоритма Пауэлла. Более подробную информацию о PowellsMethod можно найти здесь.

Использование класса CArima

Код скрипта ниже демонстрирует, как можно построить модель и оценить ее параметры для детерминированного ряда. В демонстрации, представленной в сценарии, будет сгенерирован детерминированный ряд с возможностью указания постоянного значения смещения и добавления случайного компонента, который будет имитировать шум.

Скрипт включает Arima.mqh и заполняет входной массив рядом, построенным из детерминированного и случайного компонента.

#include<Arima.mqh>

input bool Add_Noise=false;
input double Const_Offset=0.625;

Мы объявляем объект CArima, определяющий чистую модель AR(2). Вызывается метод Fit() с входным массивом и с помощью функции Summary() выводятся результаты обучения. Вывод скрипта показан ниже.

double inputs[300];
   ArrayInitialize(inputs,0);

   int error_code;

   for(int i=2; i<ArraySize(inputs); i++)
     {
      inputs[i]= Const_Offset;
      inputs[i]+= 0.5*inputs[i-1] - 0.3*inputs[i-2];
      inputs[i]+=(Add_Noise)?MathRandomNormal(0,1,error_code):0;
     }

   CArima arima(2,0,0,Const_Offset!=0);

   if(arima.Fit(inputs))
      Print(arima.Summary());

Скрипт запускается дважды с компонентом шума и без него. При первом прогоне мы видим, что алгоритм смог оценить точные коэффициенты ряда. При втором прогоне с добавленным шумом алгоритм неплохо воспроизвел истинное постоянное смещение и коэффициенты, определяющие наш ряд.

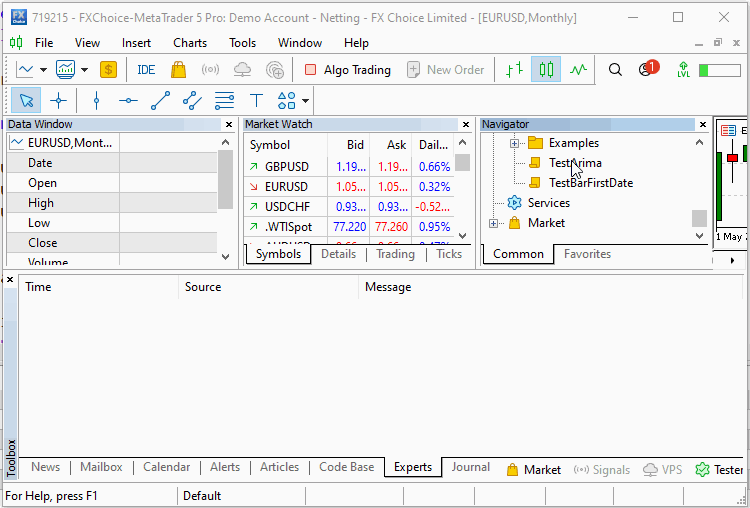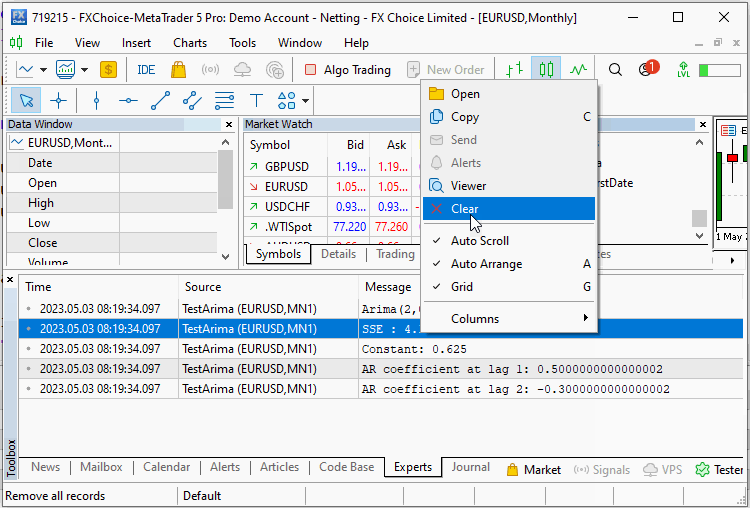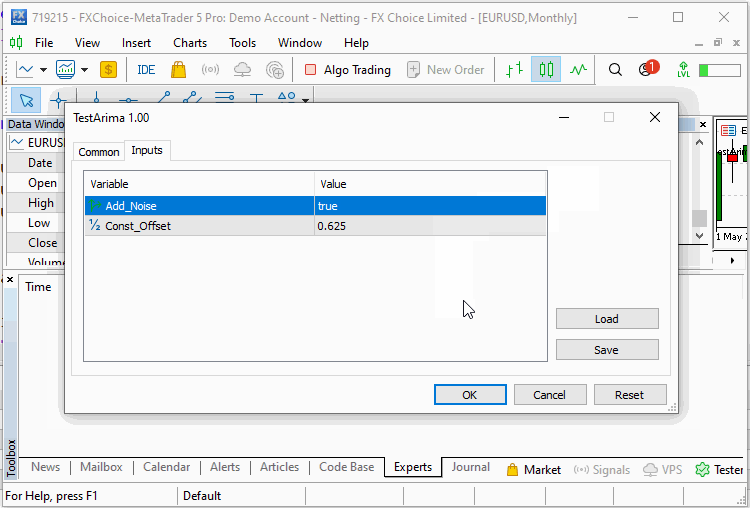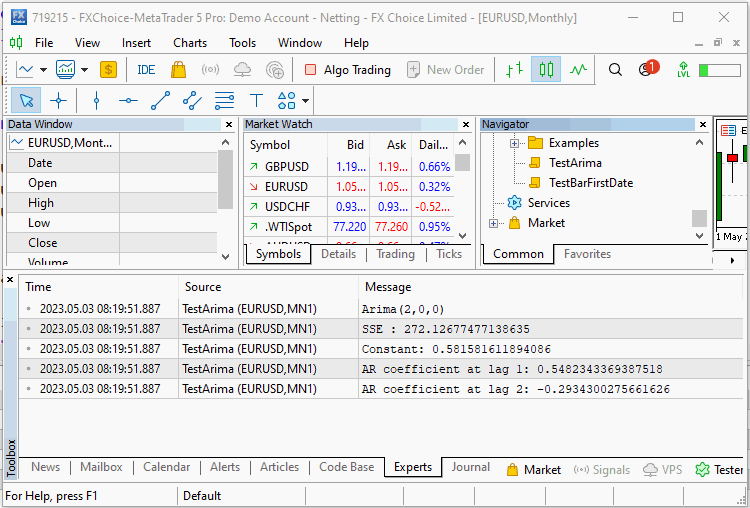
Продемонстрированный пример явно не похож на тот тип анализа, с которым мы столкнемся в реальном мире. Шум, добавленный к ряду, был умеренным по сравнению с шумом, обнаруженным в финансовых временных рядах.

Разработка моделей ARIMA

До сих пор мы рассматривали реализацию алгоритма авторегрессионного обучения, не указывая, как получить или выбрать соответствующий порядок для модели. Обучение модели, вероятно, самая простая часть дела, в отличие от определения хорошей модели.

Два полезных инструмента для получения подходящей модели — это вычисление автокорреляции и частичной автокорреляции исследуемого ряда. Рассмотрим четыре гипотетических ряда, которые помогут читателям интерпретировать графики автокорреляции и частичной автокорреляции.
                                                                  y(t) = AR1* y(t-1) +  E(t)           (3) 

                 
                                                                  y(t) = E(t) - AR1 * y(t-1)            (4) 

            
                                                                  y(t) = MA1 * E(t-1) +  E(t)          (5) 

                
                                                                   y(t) = E(t) - MA1 * E(t-1)           (6) 

    
(3) и (4) — чистые AR(1)-процессы с положительными и отрицательными коэффициентами соответственно. (5) и (6) — это чистые МА(1)-процессы с положительными и отрицательными коэффициентами соответственно.  

Изображения выше показывают автокорреляции (3) и (4) соответственно. На обоих графиках значения корреляции становятся меньше по мере увеличения запаздывания. Это имеет смысл, поскольку влияние предыдущего значения на текущее уменьшается по мере продвижения вверх по ряду.

На следующих рисунках показаны графики частичных автокорреляций той же пары рядов. Мы видим, что значения корреляции обрезаются после первого запаздывания. Эти наблюдения обеспечивают основу для общего правила о моделях AR. В целом, если частичные автокорреляции обрываются за пределами определенного запаздывания, и автокорреляции одновременно начинают затухать за пределами того же запаздывания, то ряд может быть смоделирован чистой моделью AR вплоть до наблюдаемого предельного запаздывания на графике частичной автокорреляции.

 Как видите, графики идентичны частичным автокорреляциям AR(1).

В целом, если все автокорреляции за пределами определенного пика или впадины равны нулю, а частичные автокорреляции становятся все меньше по мере того, как выбирается большее количество задержек, то ряд может быть определен составляющей MA при наблюдаемом предельном запаздывании на графике автокорреляции.

 
Другие способы определения параметров p и q модели включают:

• Информационные критерии: Существует несколько информационных критериев, таких как Информационный критерий Акаике (AIC) и Байесовский информационный критерий (BIC), которые можно использовать для сравнения различных моделей ARIMA и выбора лучшей.

• Поиск по сетке включает в себя подбор разных моделей ARIMA с разными порядками в одном и том же наборе данных и сравнение их производительности. Порядок, дающий наилучшие результаты, выбирается как оптимальный порядок ARIMA.

• Перекрестная проверка временных рядов включает в себя разделение данных временных рядов на наборы для обучения и тестирования, подгонку различных моделей ARIMA к набору для обучения и оценку их эффективности на наборе для тестирования. Порядок ARIMA, дающий наилучшую ошибку теста, выбирается в качестве оптимального порядка.

Важно отметить, что не существует универсального подхода к выбору порядка ARIMA, и для определения наилучшего порядка для вашего конкретного временного ряда может потребоваться метод проб и ошибок, а также знание предметной области.

Заключение

Мы продемонстрировали класс CArima, который инкапсулирует алгоритм авторегрессионного обучения с использованием метода минимизации функций Пауэллса. Код полного класса приведен в прикрепленном ниже zip-файле вместе со скриптом, демонстрирующим его использование.

Файл	Описание
Arima.mqh	файл include с определением класса CArima
PowellsMethod.mqh	файл include с определением класса PowellsMethod
TestArima	скрипт, демонстрирующий использование класса CArima для анализа частично детерминированного ряда.