Teoría de categorías en MQL5 (Parte 1)

Introducción

La teoría de categorías es un área de las matemáticas creada por Eilenberg y Mac Lane en la década de los 40 del siglo pasado. Sus ideas nacieron en un momento en el que la teoría de la relatividad de Einstein descubrió al mundo que no existe una única perspectiva desde la que estudiar este, sino que el verdadero poder reside en ser capaz de convertir un cierto punto de vista en otro lenguaje. Para ofrecer una definición muy breve, diremos que la teoría es un tipo de clasificación que no se limita a clasificar los objetos como tales, sino que se centra en la interrelación de dichos objetos. El valor de este enfoque reside en que los conceptos tomados de un campo de estudio o disciplina pueden ser intuitivamente comprensibles o incluso aplicables en otro campo. Inicialmente, la teoría se aplicaba al estudio de la relación entre la geometría y el álgebra. Hoy en día, el alcance de su aplicación se encuentra claramente más allá del alcance de las matemáticas y es demasiado amplio para los artículos de esta serie, por lo que nos centraremos en su posible uso para los tráders que utilizan el lenguaje de programación MQL.

En el contexto del comercio y la escritura de asesores expertos en MQL5, la teoría de categorías se puede usar para analizar y comprender las relaciones entre diferentes estrategias comerciales, instrumentos y condiciones de mercado. Asimismo, puede ayudar a los tráders a identificar patrones y estructuras comunes en sus sistemas comerciales y desarrollar algoritmos comerciales más generales y flexibles que puedan adaptarse a las condiciones cambiantes del mercado.

La teoría de categorías también puede resultar útil al verificar la corrección y consistencia de los sistemas comerciales, así como para desarrollar modelos formales de comportamiento comercial. Ofreciendo un lenguaje claro y riguroso para expresar y razonar sobre conceptos comerciales, la teoría de categorías puede ayudar a los tráders a crear asesores expertos más sólidos y fáciles de mantener, así como a compartir sus ideas y estrategias de forma más eficaz con otros tráders e investigadores.

Dominios y morfismos

Los dominios de categorías y los morfismos son los conceptos fundamentales de la teoría de categorías. Una categoría es una colección de dominios (conjuntos) de elementos y los morfismos (o flechas, también conocidas como mapas, o funciones) entre ellos. Dentro de esta serie de artículos, tomaremos las flechas, funciones o mapas como unidades básicas del morfismo. Estos morfismos codificarán las relaciones entre los elementos en cada dominio dentro de una categoría y podrán componerse para formar morfismos más complejos.

Los conjuntos son un concepto fundamental en matemáticas y juegan un papel clave en la teoría de categorías. En la teoría de categorías, los llamamos dominios, usados para definir los elementos de un "tipo" particular. Normalmente, al estudiar una categoría de dominios, los "elementos" de la categoría son los propios dominios. Estos dominios normalmente (aunque no siempre) contienen otros elementos que forman la base del morfismo. Los morfismos de esta categoría son funciones entre los dominios que suponen reglas que relacionan cada elemento de un dominio con un elemento único de otro dominio. Por ejemplo, tenemos dos dominios A y B, donde el morfismo de A hasta B sería una regla que asigna cada elemento de A a un único elemento de B. Cuando el morfismo se realiza de A hasta B, A se llama "dominio", mientras que B se llama "codominio". Todos los elementos del dominio estarán asociados con al menos uno de los elementos del dominio de códigos. Ningún elemento del dominio queda sin mapear. No obstante, es posible que no se muestren algunos elementos en el dominio del código. Esto se suele indicar de la siguiente manera.

//+------------------------------------------------------------------+
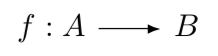
//| ELEMENT CLASS                                                    |
//+------------------------------------------------------------------+
class CElement
   {
      protected:
      
      int                           cardinal;
      vector                        element;
      
      public:
      
      bool                          Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; element.Init(cardinal); return(true); } return(false); }
      int                           Cardinality() { return(cardinal); }
      
      double                        Get(int Index) { if(Index>=0 && Index<Cardinality()) { return(element[Index]); } return(EMPTY_VALUE); }
      bool                          Set(int Index,double Value) { if(Index>=0 && Index<Cardinality()) { element[Index]=Value; return(true); } return(false); }
      
                                    CElement(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CElement(void) {};
   };

Entonces, usando la lista anterior, podremos comenzar definiendo un elemento. Esta es la unidad básica del dominio, que podemos considerar como un "miembro del conjunto". Este bloque puede aceptar cualquier tipo de datos, ya sea doble o entero, sin embargo, el tipo de vector será más flexible, ya que estamos tratando con operaciones y tipos de datos más complejos. El tipo de vector posibilita la escalabilidad. Su tamaño (el parámetro «cardinal») está protegido y solo se puede acceder o modificar usando la función 'Cardinality()'. La protección de acceso asegura que cada vez que cambie, el tamaño del vector cambiará en consecuencia. El "elemento" del propio vector también estará protegido para evitar errores de índice. Por tanto, solo se permitirá el acceso a través de las funciones 'Get()' y 'Set()'. La función 'Set()' también retornará un valor booleano para verificar si la asignación ha tenido éxito.

//+------------------------------------------------------------------+
//| DOMAIN CLASS                                                     |
//+------------------------------------------------------------------+
class CDomain
   {
      protected:
      
      int                           cardinal;
      CElement                      elements[];
      
      public:
      
      bool                          Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; ArrayResize(elements,cardinal); return(true); } return(false); }
      int                           Cardinality() { return(cardinal); }
      
      bool                          Get(int Index,CElement &Element) { if(Index>=0 && Index<Cardinality()) { Element=elements[Index]; return(true); } return(false); }
      bool                          Set(int Index,CElement &Value,bool IsNew=false) { if(Index>=0 && Index<Cardinality()) { if(!IsNew||New(Value)<0) { elements[Index]=Value; return(true); }} return(false); }
      
      //only unique elements allowed
      int                           New(CElement &Value)
                                    {
                                       bool _new=-1;
                                       //
                                       for(int o=0; o<cardinal; o++)
                                       {
                                          if(ElementMatch(Value,elements[o]))
                                          {
                                             _new=o;
                                             break;
                                          }
                                       }
                                       
                                       return(_new);
                                    }
      
                                    CDomain(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CDomain(void) {};
   };

Por lo tanto, la clase de dominio incluirá nuestros elementos, cuya clase hemos descrito antes. Sus principales variables 'elements[]' y el tamaño ('cardinal') estarán protegidas, ya que se encuentran en la clase de elementos, por las razones ya mencionadas. Lo que resulta ligeramente distinto aquí es la adición del método 'New()'. Esta función ayuda a verificar los nuevos objetos añadidos al dominio y garantiza que sean únicos. Los dominios de categorías contienen solo objetos únicos, no se permiten duplicados. 

Como tenemos estas dos clases, podríamos intentar crear varios dominios. Intentaremos obtener un dominio de números pares y un dominio de números impares. Para ello, ejecutemos un script que haga referencia a estas clases. A continuación, le mostraremos el listado.

//+------------------------------------------------------------------+
//| INPUTS                                                           |
//+------------------------------------------------------------------+
input int __domain_elements=3;
input int __domain_morphisms=5;

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
   {
      //Declare a sets of natural even & odd numbers
      CDomain _evens,_odds;
      CreateNumberDomain(_evens,__domain_elements,2);
      CreateNumberDomain(_odds,__domain_elements,2,1);
      
      printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens));
      
      printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds));
   }

La función de creación de números será un método simple para llenar un dominio con números naturales. El código completo se adjunta a este artículo. Para mayor claridad, aquí presentaremos el conjunto correspondiente.

Nos referiremos a la función 'PrintSet()' con frecuencia. Esta nos permite inspeccionar fácilmente el contenido de un dominio con los paréntesis y comas correspondientes, separando la(s) estructura(s) del vector de elementos de la estructura general del dominio.  Al ejecutar el script anterior, podremos ver lo siguiente.

2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() evens are... {(2.0),(4.0),(6.0),(8.0),(10.0),(12.0),(14.0)}

2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() odds are... {(1.0),(3.0),(5.0),(7.0),(9.0),(11.0),(13.0)}

Los diversos elementos de cada dominio están encerrados entre paréntesis porque son un tipo de datos vectoriales, lo cual significa que ellos mismos pueden tener múltiples entradas. Cuando esto sucede, aparecen comas entre cada entrada y los corchetes para ayudar a definir los límites del elemento.

Los morfismos también son un concepto importante en la teoría de categorías, y se utilizan para codificar las relaciones entre los elementos de un dominio o dominios. Según las reglas de la teoría de categorías, cada morfismo asigna un elemento de dominio a un elemento de codominio: estas funciones se pueden combinar para formar morfismos más complejos. Como veremos, pueden usarse para estudiar las propiedades de los conjuntos y las relaciones de estos con otros conjuntos.

Para empezar, existen 5 tipos principales de morfismos que se pueden usar para describir las relaciones entre objetos en una categoría dada. Algunos de los tipos más comunes son:

1. Monomorfismos: son morfismos inyectivos que mapean cada elemento del dominio de origen en un objeto de codominio único . En el mismo objeto de codominio, no pueden aparecer dos morfismos. En este caso, es posible que tengamos objetos sin mapear en el objetivo.
2. Epimorfismos: morfismos sobreyectivos. Los elementos de dominio representarán todos los elementos del codominio. En otras palabras, ningún elemento del dominio del código quedará sin mostrar. En este caso, el codominio suele contener menos elementos que el conjunto original.
3. Isomorfismos: morfismos biyectivos que establecen una correspondencia unívoca entre los objetos de las categorías de origen y objetivo. Ambos son tanto inyectivos como sobreyectivos, porque los conjuntos de origen y objetivo tienen el mismo número de objetos.
4. Endomorfismos: morfismo de un objeto de categoría en sí mismo. Esto es lo que constituye un mapa de identidad, es decir, un grupo de endomorfismos que regresan a un dominio.
5. Automorfismos: combinación de mapas de isomorfismos y endomorfismos.

Vamos a ver cómo podemos implementar en MQL una clase de morfismo y su agrupación con dominios llamados homomorfismos.

//+------------------------------------------------------------------+
//| MORPHISM CLASS                                                   |
//+------------------------------------------------------------------+
class CMorphism
   {
      public:
      
      int                           domain;
      int                           codomain;
      
      CElement                      morphism;
      
      bool                          Morph(CDomain &D,CDomain &C,CElement &DE,CElement &CE,bool Add=true)
                                    {
                                       int _d=D.New(DE),_c=C.New(CE);
                                       //
                                       if(_d>=0 && _c>=0)
                                       {
                                          if(DE.Cardinality()==CE.Cardinality())
                                          {
                                             domain=_d;
                                             codomain=_c;
                                             
                                             morphism.Cardinality(DE.Cardinality());
                                             
                                             if(Add)
                                             {
                                                for(int c=0;c<morphism.Cardinality();c++)
                                                {
                                                   morphism.Set(c,CE.Get(c)-DE.Get(c));
                                                }
                                             }
                                             else
                                             {
                                                for(int c=0;c<morphism.Cardinality();c++)
                                                {
                                                   if(DE.Get(c)!=0.0){ morphism.Set(c,CE.Get(c)/DE.Get(c)); }
                                                }
                                             }
                                          }
                                       }
                                       
                                       return(false);
                                    }
      
      
                                    CMorphism(void){ domain=-1; codomain=-1; };
                                    ~CMorphism(void){};
   };

La clase Morphism es muy simple y contiene solo los parámetros del índice de dominio y codominio, así como la función 'Morph', que no trataremos en este artículo. Aquí no se hace referencia a los conjuntos correspondientes de dominios y codominios porque se enumeran bajo la clase general Homomorphism, mostrada a continuación.

//+------------------------------------------------------------------+
//| HOMO-MORPHISM CLASS                                              |
//+------------------------------------------------------------------+
class CHomomorphism
   {
      protected:
      
      int                           cardinal;
      
      CMorphism                     morphism[];
      
      public:
      
      bool                          init;
      
      CDomain                       domain;
      CDomain                       codomain;
      
      bool                          Cardinality(int DomainIndex,int CodomainIndex,bool Add=true)
                                    { 
                                       bool _morphed=true; 
                                       
                                       if
                                       (
                                       !init
                                       )
                                       {
                                          _morphed=false; return(_morphed); 
                                       }
                                       
                                       if
                                       (
                                       DomainIndex<0 || DomainIndex>=domain.Cardinality() ||
                                       CodomainIndex<0 || CodomainIndex>=codomain.Cardinality()
                                       )
                                       {
                                          _morphed=false; return(_morphed); 
                                       }
                                       
                                       for(int m=0;m<cardinal;m++)
                                       {
                                          if(DomainIndex==morphism[m].domain)
                                          {
                                             _morphed=false; break;
                                          }
                                       } 
                                       
                                       if(_morphed)
                                       {
                                          cardinal++;
                                          ArrayResize(morphism,cardinal);
                                          CElement _de,_ce;
                                          if(domain.Get(DomainIndex,_de) && codomain.Get(CodomainIndex,_ce))
                                          {
                                             morphism[cardinal-1].Morph(domain,codomain,_de,_ce,Add);
                                          }
                                       }
                                       
                                       return(_morphed); 
                                    };
      
      int                           Cardinality()
                                    {
                                       return(cardinal);
                                    };
                                    
      bool                          Get(int Index,CMorphism &Morphism)
                                    {
                                       if(Index>=0 && Index<Cardinality())
                                       {
                                          
                                          return(true);
                                       }
                                       
                                       return(false);
                                    };
                                    
      bool                          Set(int Index,CMorphism &Value)
                                    {
                                       if
                                       (
                                       Index>=0 && Index<Cardinality() && 
                                       Value.domain>=0 && Value.domain<domain.Cardinality() &&
                                       Value.codomain>=0 && Value.codomain<codomain.Cardinality()
                                       )
                                       {
                                          if(!MorphismMatch(Index,Value,morphism,Cardinality()))
                                          {
                                             morphism[Index]=Value;
                                             return(true);
                                          }
                                          
                                       }
                                       
                                       return(false);
                                    };
                                    
      void                          Init(CDomain &Domain,CDomain &Codomain)
                                    {
                                       domain=Domain;
                                       codomain=Codomain;
                                       
                                       init=true;
                                    }
      
      
                                    CHomomorphism(void){ init=false; cardinal=0; };
                                    ~CHomomorphism(void){};
   };

En la clase Homomorphism se protege la variable 'morphism[]' junto con su tamaño 'morphisms' por las razones ya mencionadas. Baste decir que las dos funciones 'Morphism()' así como las funciones 'Get()' y 'Set()' son similares a las funciones en las clases de objetos y conjuntos. Aquí hemos añadido el parámetro booleano 'init' que indica si la clase se ha inicializado asignando los conjuntos públicos 'dominio' y 'codominio'. La adición de un morfismo al array protegido 'morphism[]' se realiza proporcionando los índices de dominio y codominio. Estos índices deberán encontrarse dentro del rango de tamaño de los respectivos dominios. Tras pasar por el rango, deberemos verificar, en particular, que no se haya utilizado el índice de dominio. Según las reglas de la teoría de categorías, todos los objetos en un dominio deberán asignarse a un objeto de codominio una sola vez, por lo tanto, un índice de codominio se podrá usar dos veces, mientras que un índice de dominio solo se podrá usar una vez.

Vamos a permitirnos una pequeña digresión y a ver los subdominios (también conocidos como subconjuntos). Los subdominios son una herramienta útil en la teoría de categorías y nos permiten enumerar subdominios dentro de un dominio y/o verificar si un dominio es un posible subdominio para un dominio determinado. Veamos las funciones que realizan estas dos tareas.

//+------------------------------------------------------------------+
//| Domain Match function                                            |
//+------------------------------------------------------------------+
bool DomainMatch(CDomain &A,CDomain &B)
   {
      if(A.Cardinality()!=B.Cardinality())
      {
         return(false);
      }
      
      bool _matched=true;
      
      for(int o=0; o<A.Cardinality(); o++)
      {
         CElement _a,_b;
         
         if(A.Get(o,_a) && B.Get(o,_b) && !ElementMatch(_a,_b))
         {
            _matched=false; break;
         }
      }
      
      return(_matched);
   }
//+------------------------------------------------------------------+
//| Is Subdomain function                                            |
//+------------------------------------------------------------------+
bool IsSubdomain(CDomain &Domain,CDomain &SubDomain)
   {
      bool _is_subdomain=false;
      
      int _subdomain_count=0; CDomain _subdomains[];
      GetSubdomains(Domain,_subdomain_count,_subdomains);
      
      for(int c=0;c<_subdomain_count;c++)
      {
         if(DomainMatch(SubDomain,_subdomains[c]))
         {
            _is_subdomain=true;
            break;
         }
      }
      
      return(_is_subdomain);
   }

Propiamente, si ejecutamos el siguiente script:

//+------------------------------------------------------------------+
//| INPUTS                                                           |
//+------------------------------------------------------------------+
input int __domain_elements=3;
input int __domain_morphisms=5;

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
   {
      //Declare a sets of natural even & odd numbers
      CDomain _evens,_odds;
      CreateNumberDomain(_evens,__domain_elements,2);
      CreateNumberDomain(_odds,__domain_elements,2,1);
      
      printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens));
      
      printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds));
    
      int _subdomain_count=0; CDomain _subdomains[];
      GetSubdomains(_evens,_subdomain_count,_subdomains);
      printf(__FUNCSIG__+" evens subs are... "+IntegerToString(_subdomain_count));
      for(int s=0; s<_subdomain_count; s++)
      {
         printf(" with: "+PrintDomain(_subdomains[s])+", at: "+IntegerToString(s+1));
      }
   } 

En los logs veremos las siguientes entradas:

2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) void OnStart() evens subs are... 7

2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) with: {(2.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 1

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 2

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 3

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 4

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 5

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 6

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 7

El número real de subconjuntos posibles es 8 si incluimos el conjunto vacío, que también es un subconjunto.

El código adicional para la verificación de subconjuntos podría tener el aspecto que sigue:

      CDomain _smaller_evens;
      CreateNumberDomain(_smaller_evens,__domain_elements-2,2);
      
      printf(__FUNCSIG__+" smaller evens are... "+PrintDomain(_smaller_evens));
      
      bool _is_subdomain=IsSubdomain(_evens,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of evens. ");
      _is_subdomain=IsSubdomain(_odds,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of odds. ");
      

En los logs veremos lo siguiente:

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) void OnStart() smaller evens are... {(2.0)}

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1)

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: true that 'smaller-evens' is a subset of evens. 

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: false that 'smaller-evens' is a subset of odds. 

En la teoría de categorías, un homomorfismo es una definición que conserva la estructura de un grupo de morfismos entre dos dominios. Se trata de una función que conserva las relaciones y operaciones definidas para los elementos. Los homomorfismos son importantes en la teoría de categorías porque ofrecen un medio para estudiar las relaciones entre diferentes elementos y construir nuevos elementos a partir de los ya existentes.

Teniendo en cuenta los homomorfismos entre elementos, podemos hacernos una idea sobre la naturaleza de los elementos y su comportamiento en diferentes varias operaciones. Por ejemplo, la existencia de un homomorfismo entre dos dominios puede utilizarse para definir el concepto de equivalencia entre ellos, que permite estudiar la relación entre ambos.

Otro valor de los homomorfismos en la teoría de categorías es que ofrecen un medio para construir nuevos objetos a partir de los existentes al heredar estas propiedades. Los ejemplos relevantes, junto con las equivalencias, se discutirán en artículos posteriores y solo los mencionaremos aquí para establecer una base que defina esta clase aparentemente "inútil".

Para nuestros propósitos, intentaremos darle vida a la teoría de categorías creando un ejemplar de clase de homomorfismo que tenga múltiples dominios y codominios de horas de cierre y precios.

Luego analizaremos este ejemplar usando la función 'PrintHomomorphism()'. Estas funciones definidas por el usuario resultarán muy útiles al visualizar los objetos, conjuntos, morfismos y homomorfismos creados. El listado se muestra a continuación:

//+------------------------------------------------------------------+
//| Print Element function                                           |
//+------------------------------------------------------------------+
string PrintElement(CElement &O,int Precision=1,bool IsTime=false)
   {
      string _element="(";
      //
      for(int r=0; r<O.Cardinality(); r++)
      {
         if(!IsTime)
         {
            _element+=DoubleToString(O.Get(r),Precision);
         }
         else if(IsTime)
         {
            _element+=TimeToString(datetime(int(O.Get(r))));
         }
         
         if(r<O.Cardinality()-1){ _element+=","; }
      }
      //
      return(_element+")");
   }
//+------------------------------------------------------------------+
//| Print Set function                                               |
//+------------------------------------------------------------------+
string PrintDomain(CDomain &S,int Precision=1,bool IsTime=false)
   {
      string _set="{";
      //
      CElement _e;
      for(int o=0; o<S.Cardinality(); o++)
      {
         S.Get(o,_e);
         _set+=PrintElement(_e,Precision,IsTime);if(o<S.Cardinality()-1){ _set+=","; }
      }
      //
      return(_set+"}\n");
   }
//+------------------------------------------------------------------+
//| Print Morphism function                                          |
//+------------------------------------------------------------------+
string PrintMorphism(CMorphism &M, CDomain &Domain,CDomain &Codomain,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false)
   {
      string _morphism="";
      //
      CElement _d,_c;
      if(Domain.Get(M.domain,_d) && Codomain.Get(M.codomain,_c))
      {
         _morphism=PrintElement(_d,Precision,DomainIsTime);
         _morphism+="|----->";
         _morphism+=PrintElement(_c,Precision,CodomainIsTime);
         _morphism+="\n";
      }
      //
      return(_morphism);
   }
//+------------------------------------------------------------------+
//| Print Homomorphism function                                      |
//+------------------------------------------------------------------+
string PrintHomomorphism(CHomomorphism &H,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false)
   {
      string _homomorphism="\n\n"+PrintDomain(H.domain,Precision,DomainIsTime);
      //
      _homomorphism+="|\n";
      
      CMorphism _m;
      for(int m=0;m<H.Cardinality();m++)
      {
         if(H.Get(m,_m))
         {
            _homomorphism+=(PrintMorphism(_m,H.domain,H.codomain,Precision,DomainIsTime,CodomainIsTime));
         }
      }
      //
      _homomorphism+="|\n";
      
      _homomorphism+=PrintDomain(H.codomain,Precision,CodomainIsTime);
      //
      return(_homomorphism);
   }

Las entradas notables aquí son 'Precision' e 'IsTime'.'. Estas dos opciones establecen los decimales para mostrar los datos flotantes (por defecto para los vectores) y determinan si es necesario convertir los datos del objeto/vector en tiempo para su presentación en la cadena retornada. 

Para crear un homomorfismo, usaremos el siguiente script:

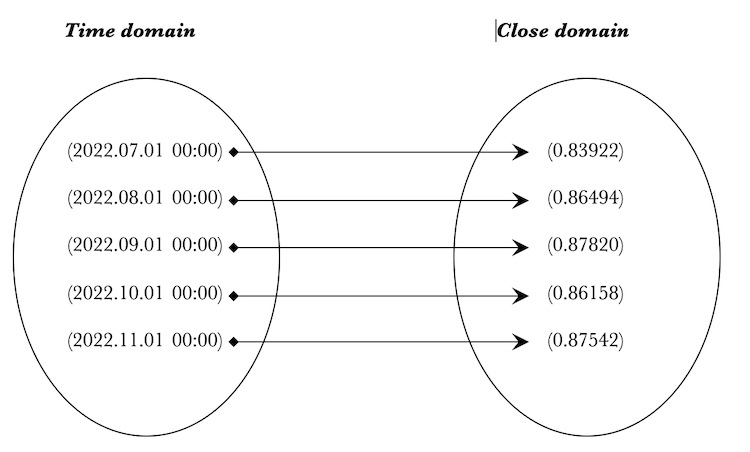
//Declare sets to store time & close prices
      CDomain _time,_close;
      
      MqlRates _rates[];
      
      //Fill domain with 5 most recent bar time & MA values from chart
      if(CopyRates(_Symbol,_Period,0,__domain_morphisms,_rates)>=__domain_morphisms && _time.Cardinality(__domain_morphisms) && _close.Cardinality(__domain_morphisms))
      {
         for(int m=0;m<__domain_morphisms;m++)
         {
            //Create uni row element
            CElement _t,_m;
            if(_t.Cardinality(1) && _m.Cardinality(1))
            {
               datetime _t_value=_rates[m].time;//iTime(_Symbol,_Period,m);
               _t.Set(0,double(int(_t_value)));
               _time.Set(m,_t);
               
               double _m_value=_rates[m].close;//iClose(_Symbol,_Period,5);//,m,MODE_SMA,PRICE_CLOSE);
               _m.Set(0,_m_value);
               _close.Set(m,_m);
            }
         }
      }
      
      //Create homomorphism from time to close
      CHomomorphism _h;_h.Init(_time,_close);
      
      if(_h.init)
      {
         //Create 1-1 morphisms from time to MA
         int _morphisms=0;
         for(int m=0;m<__domain_morphisms;m++)
         {
            if(_h.Cardinality(m,m)){ _morphisms++; }
         }
         
         if(_morphisms>=__domain_morphisms)
         { 
            printf(__FUNCSIG__+" homomorphism: "+PrintHomomorphism(_h,_Digits,true)); 
         }
      }

Así, crearemos dos conjuntos: '_time' y "_close'. Luego los rellenaremos con los datos del array MqlRates. '__set_morphisms' es un parámetro de entrada que define el tamaño del conjunto. En este caso, los conjuntos '"time" y "_close" tendrán el mismo tamaño y se corresponderán con el parámetro de entrada. Luego se inicializará un ejemplar de la clase de homomorfismo '_h' con estos dos conjuntos. Los morfismos mutuamente unívocos simples se crean entre dos conjuntos usando la función 'Morphisms()'. Esta se comprueba porque retorna un valor lógico. Si es true, se incrementará el parámetro '_morphisms'. Una vez obtengamos el tamaño del parámetro de entrada, imprimiremos el homomorfismo '_h' usando la función Print Homomorphism()'. En los logs veremos lo siguiente:

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) void OnStart() homomorphism: 

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(2022.07.01 00:00),(2022.08.01 00:00),(2022.09.01 00:00),(2022.10.01 00:00),(2022.11.01 00:00)}

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) |

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.07.01 00:00)|----->(0.83922)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.08.01 00:00)|----->(0.86494)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.09.01 00:00)|----->(0.87820)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.10.01 00:00)|----->(0.86158)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.11.01 00:00)|----->(0.87542)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) |

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(0.83922),(0.86494),(0.87820),(0.86158),(0.87542)}

En la teoría de categorías, también puede resultar útil enumerar el conjunto de imágenes de un homomorfismo. La imagen simplemente se referirá a un subconjunto del codominio en el que solo se representarán los objetos asociados con el dominio. Para nuestros propósitos, podemos realizar una enumeración usando la siguiente función:

//+------------------------------------------------------------------+
//| Image function                                                   |
//+------------------------------------------------------------------+
void Image(CHomomorphism &H,CSet &Output)
   {
      for(int m=0;m<H.Morphisms();m++)
      {
         CObject _o;
         CMorphism _m;
         if(H.Get(m,_m) && H.codomain.Get(_m.codomain_index,_o))
         {
            bool _matched=false;
            for(int o=0;o<Output.Objects();o++)
            {
               CObject _oo;
               if(Output.Get(o,_oo) && ObjectMatch(_o,_oo))
               {
                  _matched=true; break;
               }
            }
            
            if(!_matched)
            {
               Output.Objects(Output.Objects()+1);
               Output.Set(Output.Objects()-1,_o);
            }
         }
      }
   }

Para ver este código en acción, usaremos el siguiente script:

      //Create homomorphism from time to close
      CHomomorphism _h_image;_h_image.Init(_time,_close);
      
      if(_h_image.init)
      {
         //Create 1-1 morphisms from time to MA
         int _morphisms=0;
         for(int m=0;m<__set_morphisms;m++)
         {
            int _random_codomain=MathRand()%__set_morphisms;
            if(_h_image.Morphisms(m,_random_codomain)){ _morphisms++; }
         }
         
         if(_morphisms>=__set_morphisms)
         { 
            CSet _image;_image.Objects(0);
            Image(_h_image,_image);
            printf(__FUNCSIG__+" image from homomorphism: "+PrintSet(_image,_Digits)); 
         }
      }

Todo lo que hacemos aquí es usar los dos conjuntos que creamos anteriormente en una nueva clase de homomorfismo llamada '_h_image'. La diferencia esta vez es que al añadir morfismos, elegimos aleatoriamente los valores de codominio y así obtenemos una repetición. Esto significa que el conjunto de codominios será diferente de lo especificado en la instancia '_h'. En los logs veremos las siguientes entradas:

2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2) void OnStart() image from homomorphism: {(145.847),(145.188)}

2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2)

Obviamente, el codominio tiene solo dos objetos de tres posibles, por lo que podremos obtener fácilmente objetos asociados con un conjunto dado. En el próximo artículo, analizaremos los isomorfismos y endomorfismos.

Conclusión

En el presente artículo, hemos visto algunos conceptos introductorios de la teoría de categorías, un método matemático productivo para clasificar información. Entre ellos se encuentran el elemento, el dominio y el morfismo. Un elemento forma una unidad fundamental y generalmente se considera como miembro de un conjunto, que en la teoría de categorías se denomina dominio. Este dominio, a través de sus elementos, puede relacionarse con otros dominios (llamados codominios). Dichas relaciones se denominan morfismos. Para un tráder, la teoría de categorías puede servir como clasificador de la información financiera sobre series temporales, suponiendo así una herramienta para evaluar y predecir las condiciones del mercado.