Популяционные алгоритмы оптимизации: Изменяем форму и смещаем распределения вероятностей и тестируем на "Умном головастике" (Smart Cephalopod, SC)

Содержание:

1. Введение
2. Тестовый стенд для проверки распределений
3. Построение случайных чисел с требуемым законом распределения
4. Шаблон для алгоритма оптимизации - Алгоритм "Умный Головастик"
5. Выводы

1. Введение

Теория вероятностей — это математическая теория, которая изучает случайные явления и определяет вероятность их возникновения. Она позволяет описывать и анализировать случайные процессы. Основными понятиями теории вероятностей являются вероятность, случайная величина, распределение вероятностей, математическое ожидание, дисперсия.

Вероятность — это числовая характеристика, которая определяет, насколько вероятно возникновение определенного события.

Случайная величина — это функция, которая ставит в соответствие каждому исходу случайного эксперимента некоторое число.

Распределение вероятностей — это функция, которая определяет вероятность возникновения каждой из возможных значений случайной величины.

Математическое ожидание — это среднее значение случайной величины, которое можно получить при многократном повторении эксперимента.

Дисперсия — это мера разброса значений случайной величины относительно ее математического ожидания.

Момент — это числовая характеристика случайной величины, которая описывает ее распределение. Моменты используются для определения центра распределения (математическое ожидание) и его разброса (дисперсия и стандартное отклонение), а также для анализа формы распределения (скошенность и эксцесс). Первый момент (n=1) - это математическое ожидание, который определяет центр распределения случайной величины. Второй момент (n=2) - это дисперсия, который описывает разброс случайной величины относительно ее математического ожидания. Третий момент (n=3) — это мера скошенности распределения, а четвертый момент (n=4) - это мера эксцесса (выпуклости) распределения.

Распределения вероятностей играют важную роль в моделировании случайных явлений и анализе данных, а также в статистике для оценки параметров и проверки гипотез. Они позволяют описать вероятностные свойства случайных величин и событий, а также определить вероятность различных исходов.

Теория вероятности и оптимизация являются двумя важными научными дисциплинами, которые находят широкое применение в различных областях науки и техники, таких как экономика, финансы, инженерия, биология, медицина и многие другие. Развитие этих областей и применение их методов исследования и оптимизации позволяет решать сложные задачи и создавать новые технологии, увеличивая эффективность и качество работы в различных сферах деятельности. Примером может послужить развитие современных технологий для создания квантовых компьютеров, безопасных супер быстрых средств связи, генеративных нейронных сетей и искусственного интеллекта. 

Вероятностные расчеты, основанные на теории вероятности, играют ключевую роль в моделировании случайных явлений и анализе данных. Оптимизация, в свою очередь, нацелена на нахождение оптимальных решений в различных задачах и позволяет найти наилучшие решения среди множества возможных вариантов. Однако, в реальных задачах существует неопределенность и случайность и именно здесь распределения вероятностей вступают в игру. Они позволяют учесть случайность и неопределенность в оптимизационных задачах.

Распределения вероятностей также активно используются в эволюционных и популяционных алгоритмах. В этих алгоритмах случайные генерации новых состояний в пространстве поиска моделируются с помощью соответствующих вероятностных распределений. Это позволяет исследовать пространство параметров и находить оптимальные решения с учетом случайности и разнообразия в популяции.

Более сложные методы оптимизации используют вероятностные распределения для моделирования неопределенности и аппроксимации сложных функций. Они позволяют эффективно исследовать пространство параметров и находить оптимальные решения с учетом случайности и шума в данных.

В данной статье мы рассмотрим различные типы вероятностных распределений, их свойства и практическую реализацию в виде соответствующих функций в коде. При генерации случайных чисел с различными видами распределений на практике можно столкнуться с большим количеством проблем, такими как бесконечность длины хвостов, смещение вероятностей при задании границ дисперсии, также при проектировании и создании алгоритмов оптимизации очень часто возникает необходимость в смещении вероятностей относительно математического ожидания. Целью данной статьи является решение этих проблем и создание рабочих функций для работы с вероятностями для их последующего применения в алгоритмах оптимизации.

2. Тестовый стенд для проверки распределений

Для тестирования и визуализации распределений случайных величин необходим тестовый стенд, который позволит наглядно отобразить форму распределений. Это важно при проектировании алгоритмов оптимизации, поскольку визуальное представление и понимание того, в какую сторону необходимо сместить вероятность случайной величины, помогает достичь наилучших результатов.

Что бы построить распределение вероятностей необходимо создать что то вроде ряда коробок, в которые будут попадать случайные числа. Коробки - по сути это счетчики. Например, имеем такую ситуацию с числовой прямой, ограниченной слева "min" и справа "max" и лежищей между ними "in", можно представить это так:

min|-----|-----|-----|-----|-----|-----|in|--|--|--|--|--|--|max

Видим, что значение "in" смещено на числовой прямой ближе к "max". Если мы будем генерировать случайные числа в диапазоне [min;max], то количество выпадений случайных чисел в диапазоне [min;in] будет больше, чем в диапазоне [in;max], тем самым вероятность выпадений чисел будет смещена влево, создастся дисбаланс, но нам необходимо, чтобы количество выпадений слева и справа было в среднем одинаковым, нам необходимо изменить форму распределения без смещения вероятностей. Для этого количество коробок слева и справа должно быть одинаковым (в схематичном примере выше - это по 6 коробок слева и справа).

Итак, тестовый стенд для построения распределений достаточно прост, суть его работы заключается в следующем:

• создаём объект CCanvas для работы с холстом
• генерируем случайное число с выбранным в настройках распределением
• проверяем, в какую область соответсвующей коробки выпало случайное число и прибавляем 1 к коробке
  
• подсчитываем минимальное и максимальное количество выпадений среди всех коробок
• рисуем круги на холсте для каждой коробки, что соответствует количеству попавших в коробки случайных чисел
• раскрашиваем круги в цвета от синего (редко) до красного (часто)
  

Общая цель кода - визуализировать вероятностное распределение на холсте с помощью графика, где каждый круг - количество выпавших в коробках случайных чисел, нормированное на min/max количество во всех коробках.

#property script_show_inputs
#include <Canvas\Canvas.mqh>

enum E_Distribution
{
  uniform = 0,
  gauss   = 1,
  power   = 2,
  levi    = 3
};

//--- input parameters
input double         MinP       = -100.0;
input double         InpP       =  0;
input double         MaxP       =  100.0;
input int            CNT        =  1000000;
input int            Size       =  1000;
input double         SigmaP     =  3;       //Sigma for "Gauss" distribution
input double         PowerP     =  2;       //Power for "Power law" distribution
input double         LeviPowerP =  2;       //Power for "Levy flights" distribution
input E_Distribution Distr_P    = gauss;    //Distribution type

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  CCanvas Canvas;

  int W = 750;
  int H = 400;
  int O = 10;

  int CountL [];
  int CountR [];

  ArrayResize     (CountL, Size);
  ArrayInitialize (CountL, 0);

  ArrayResize     (CountR, Size);
  ArrayInitialize (CountR, 0);

  string canvasName = "Test_Probability_Distribution_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }

  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN,     false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  Canvas.Erase (COLOR2RGB (clrWhite));
  Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB (clrBlack));

  int    ind = 0;
  double X   = 0.0;

  for (int i = 0; i < CNT; i++)
  {
    switch (Distr_P)
    {
    case uniform:
      X = UniformDistribution (InpP, MinP, MaxP);
      break;
    case gauss:
      X = GaussDistribution (InpP, MinP, MaxP, SigmaP);
      break;
    case power:
      X = PowerDistribution (InpP, MinP, MaxP, PowerP);
      break;
    case levi:
      X = LeviDistribution (InpP, MinP, MaxP, LeviPowerP);
      break;
    }

    if (X < InpP)
    {
      ind = (int)Scale (X, MinP, InpP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountL [ind] += 1;
    }
    else
    {
      ind = (int)Scale (X, InpP, MaxP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountR [ind] += 1;
    }
  }

  int minCNT = CNT;
  int maxCNT = 0;

  for (int i = 0; i < Size; i++)
  {
    if (CountL [i] > maxCNT) maxCNT = CountL [i];
    if (CountR [i] > maxCNT) maxCNT = CountR [i];

    if (CountL [i] < minCNT) minCNT = CountL [i];
    if (CountR [i] < minCNT) minCNT = CountR [i];
  }

  int x = 0.0;
  int y = 0.0;
  color clrF;
  int centre = 0;
  int stepL  = 0;
  int stH_L  = 0;
  int stepR  = 0;
  int stH_R  = 0;

  centre = (int)Scale (InpP, MinP, MaxP, 10, W - 11, false);

  stepL = (centre - O) / Size;
  stH_L = stepL / 2;
  if (stH_L == 0) stH_L = 1;

  stepR = (W - O - centre) / Size;
  stH_R = stepR / 2;
  if (stH_R == 0) stH_R = 1;

  for (int i = 0; i < Size; i++)
  {
    x = (int)Scale (i,          0, Size - 1, O, centre - stH_L, false);
    y = (int)Scale (CountL [i], 0, maxCNT,   O, H - O,  true);

    clrF = DoubleToColor (CountL [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));


    x = (int)Scale (i,          0, Size - 1, centre + stH_R, W - O, false);
    y = (int)Scale (CountR [i], 0, maxCNT,   O,      H - O, true);

    clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));
  }

  Canvas.Update ();
}
//——————————————————————————————————————————————————————————————————————————————

3. Построение случайных чисел с требуемым законом распределения

Равномерное распределение (Uniform distribution)

Равномерное распределение - это распределение вероятностей, при котором все значения случайной величины на заданном интервале имеют равную вероятность. Равномерное распределение широко используется для моделирования случайных величин, которые равновероятно могут принимать значения на заданном интервале.

Рисунок 1. Равномерное распределение чисел без смещения.

Самым простым в реализации среди всех является равномерное распределение. Единственным моментом, который здесь следует учесть, является то, что мы не можем просто сгенерировать числа в диапазоне [min;max], поэтому сгенерируем случайное число слева от In или справа от In в зависимости от предварительно сгенерированного случайного числа в диапазоне [0.0;1.0]. Поэтому количество сгенерированных чисел слева и справа равновероятно при любом положении In относительно [min;max]. Здесь отсутствуют какие либо проблемы с выходом из диапазона или артефактами в распределении.

Равномерное распределение мы можем использовать во всех случаях, когда необходимо сгенерировать число в заданном диапазоне с равной вероятностью выпадения на всём диапазоне.

//——————————————————————————————————————————————————————————————————————————————
double UniformDistribution (const double In, const double outMin, const double outMax)
{
  double rnd = RNDfromCI (0.0, 1.0);

  if (rnd >= 0.5) return RNDfromCI (In, outMax);
  else            return RNDfromCI (outMin, In);
}
//——————————————————————————————————————————————————————————————————————————————

Нормальное распределение (Gaussian distribution)

Нормальное распределение - это распределение вероятностей, которое описывает многие случайные явления в природе, экономике и других областях. Оно характеризуется колоколообразной формой и симметричностью относительно среднего значения. Среднее значение и дисперсия нормального распределения определяют его полностью.

Одним из ключевых свойств нормального распределения является его симметричность относительно среднего значения. Это означает, что вероятность того, что случайная величина примет значение, равное среднему значению, наибольшая, а вероятность того, что она примет значение, отличное от среднего значения, уменьшается по мере удаления от среднего значения. Это свойство делает нормальное распределение особенно полезным для моделирования и анализа данных, так как оно позволяет описывать и предсказывать случайные явления, которые имеют среднее значение и отклонения от него.

Нормальное распределение также имеет множество математических свойств, которые делают его удобным для использования в статистических методах и моделях. Например, если случайные величины независимы и имеют нормальное распределение, то их сумма также будет иметь нормальное распределение. Это свойство позволяет использовать нормальное распределение для моделирования и анализа сложных систем, состоящих из множества случайных переменных. Нормальное распределение имеет множество применений в статистике, физике, экономике, финансах и других областях. Оно является основой для многих статистических методов и моделей, таких как линейная регрессия и анализ временных рядов.

Для алгоритмов оптимизации нормальное распределение бывает полезным в случаях, когда мы хотим акцентировать внимание к определенному месту на числовой прямой. При этом нам может понадобиться только часть кривой, образующей форму рапсределния. Например, мы хотим использовать рапределение в пределах только трех стандартных отклонений, все, что выходит за эти границы мы не можем просто вернуть значения назад, на края границы. Если мы так поступим, то получим частоту выпадения на границах, превышающей частоту на среднем значении. Эта проблема продемонстрирована на рис. 2, которую решим в описании ниже.

Для генерации случайной величины с нормальным законом распределения можно использовать метод Бокса-Мюллера.

• Сначала необходимо сгенерировать два случайных равномерно распределенных числа u1 (0, 1] и u2 [0, 1]
• Затем необходимо вычислить случайную величину z0, используя формулу:

z0 = sqrt(-2 * ln(u1)) * cos(2 * pi * u2)   

• Полученная случайная величина z0 будет иметь стандартное нормальное распределение
  

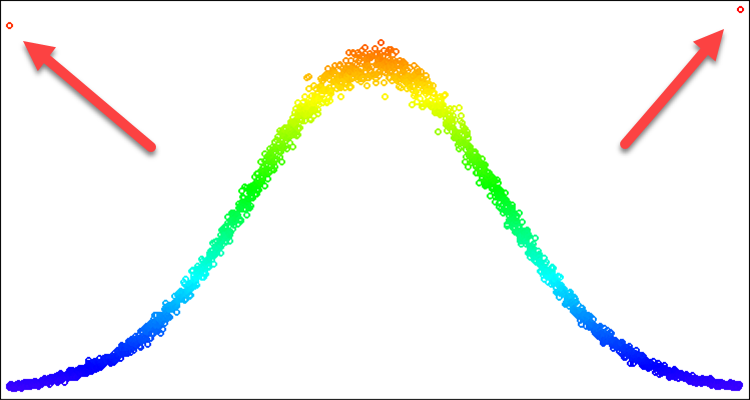
Рисунок 2. Нормальное распределение с sigma=3 и артефакты при попытке обрезать всё что дальше 3х сигм.

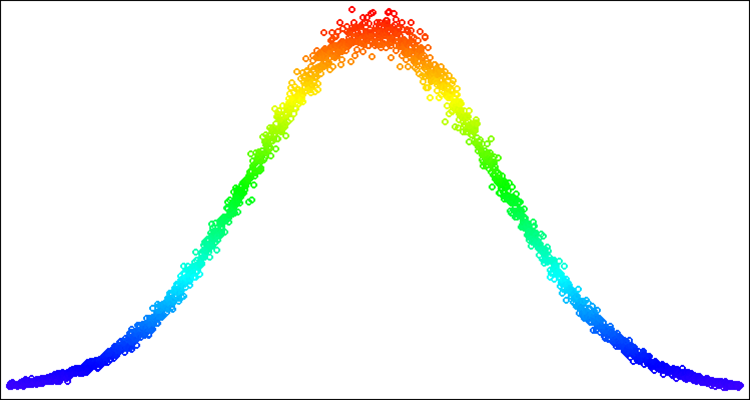
Рисунок 3. Нормальное распределение с sigma=3 с решённой проблемой артефактов (выхода за границы распределения).

Напишем реализацию функции GaussDistribution, которая генерирует случайные значения с нормальным распределением относительно среднего значения "in":

• Задаются параметры функции: входное значение (in), минимальное и максимальное значения выходного диапазона (outMin и outMax), среднеквадратическое отклонение (sigma).
• Вычисляется натуральный логарифм от u1, который генерируется случайным образом в диапазоне от 0 до 1.
• Если u1 меньше или равен 0, то logN присваивается значение 0.000000000000001, иначе logN равен u1.
• Вычисляется значение z0 с помощью формулы для нормального распределения.
• Проверяется входное значение "sigma" на выход за диапазон максимально возможного значения стандартного отклонения равного  8.583864105157389.
  
• Если z0 больше или равен sigmaN, то z0 присваивается случайное значение в диапазоне от 0 до sigmaN, иначе, если z0 меньше или равен -sigmaN, то z0 присваивается случайное значение в диапазоне от -sigmaN до 0.0. 
• Если z0 больше или равен 0, то возвращается значение, рассчитанное с помощью функции Scale для диапазона от 0 до sigmaN и выходного диапазона от "in" до "outMax", иначе возвращается значение, рассчитанное с помощью функции "Scale" для диапазона от -sigmaN до 0 и выходного диапазона от "outMin" до in.
  

Выделенное жёлтым - решение проблемы частоты выпадений на краях заданного стандартного отклонения. Таким образом мы просто "раскидываем" вероятность, выпадающую за границы, внутрь на соответствующую часть кривой распределения. При этом не нарушается форма распределения.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::GaussDistribution (const double In, const double outMin, const double outMax, const double sigma)
{
  double logN = 0.0;
  double u1   = RNDfromCI (0.0, 1.0);
  double u2   = RNDfromCI (0.0, 1.0);

  logN = u1 <= 0.0 ? 0.000000000000001 : u1;

  double z0 = sqrt (-2 * log (logN)) * cos (2 * M_PI * u2);

  double sigmaN = sigma > 8.583864105157389 ? 8.583864105157389 : sigma;

  if (z0 >=  sigmaN) z0 = RNDfromCI (0.0,     sigmaN);
  if (z0 <= -sigmaN) z0 = RNDfromCI (-sigmaN, 0.0);

  if (z0 >= 0.0) z0 =  Scale (z0,        0.0, sigmaN, 0.0, outMax - In, false);
  else           z0 = -Scale (fabs (z0), 0.0, sigmaN, 0.0, In - outMin, false);
  
  return In + z0;
}
//——————————————————————————————————————————————————————————————————————————————

Ниже пример случайных чисел с нормальным распределением на рис. 4. В этом примере и далее - распределения вокруг искомого значения "50" в диапазоне от "-100" до "100" [-100;50;100].

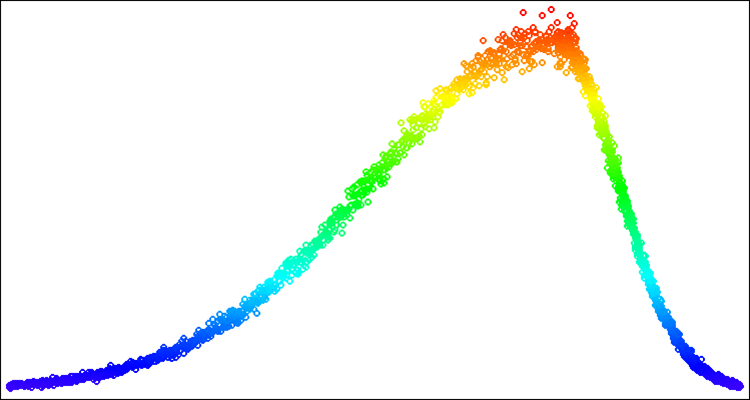
Рисунок 4. Нормальное распределение с sigma=3, [-100;50;100].

Степенное распределение (Power law distribution)

Степенное распределение - это распределение вероятности, которое описывает случайные величины, у которых вероятность того, что они примут очень большие значения, убывает по степенному закону. Такое распределение также называют законом Парето или законом Ципфа. Степенное распределение находит применение в различных областях науки и техники. Например, оно используется в физике для моделирования распределения масс и энергии в системах с многими частицами, таких как звездные скопления и галактики. Оно также используется в экономике и социологии для анализа распределения доходов и богатства.

Степенное распределение имеет несколько интересных свойств. Во-первых, оно является тяжелохвостым, что означает, что вероятность того, что случайная величина примет очень большие значения, не равна нулю. Во-вторых, оно не имеет конечного математического ожидания, что означает, что среднее значение случайной величины может быть бесконечным.

Степенное распределение имеет очень полезную, в некоторых случаях форму, для использования в алгоритмах оптимизации. Оно позволяет концентрировать плотность случайных чисел в местах пространства поиска, которые требует особого внимания, уточнения. Однако в чистом виде оно непригодно для применения, когда мы хотим четко ограничить границы случайных чисел, так как у него бесконечной длины хвосты, которые так просто, как в случае с нормальным распределением, не получится "завернуть внутрь".

Для классической реализации степенного закона распределения необходимо использовать обратную функцию, однако, для того чтобы избавиться от бесконечности в хвостах распределения, которая мешает нам при генерации значений в известных пределах, мы можем использовать равномерно распределенную величину, возведенную в степень. Хотя это не является правильным способом задания степенного закона распределения, это позволит нам избавиться от бесконечности в хвостах распределения, сохраняя при этом форму распределения, которая достаточно близка к теоретической. Для стохастических алгоритмов оптимизации это более чем достаточно.

Функция PowerDistribution принимает на вход четыре значения типа double: "in", "outMin", "outMax" и "power". Она генерирует случайное число "rnd" в диапазоне от [-1.0;1.0], вычисляет значение "r", которое является результатом возведения в степень "power", и затем масштабирует это значение из диапазона [0.0;1.0] в заданный диапазон значений с помощью функции Scale. Если "rnd" отрицательное число, то масштабирование производится в диапазон [outMin;in], иначе - в диапазон  [in;outMax]. Результат выполнения функции возвращается в качестве значения типа double.

• Если "power меньше 1, то большинство значений в полученном распределении будут сконцентрированы вблизи нуля, а хвост распределения будет сильно усечен. Такое распределение будет напоминать параболу.
• Если "power" равно 1, то полученное распределение будет равномерным.
• Если "power" больше 1, то большинство значений в полученном распределении будут распределены далеко от нуля, а хвост распределения будет длинным. Такое распределение будет иметь тяжелый хвост и будет напоминать распределение Парето или степенной закон распределения.
• Если "power" стремится к бесконечности, то полученное распределение будет напоминать дельта-функцию, сосредоточенную в нуле.

Таким образом, нам открывается поле дополнительных возможностей с использованием разного значения степени "power", следовательно и больше возможностей с исследованием для выбора оптимального распределения для получения наилучшего результата в алгоритме оптимизации в контексте решения конкретной задачи оптимизации.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::PowerDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double rnd = RNDfromCI (-1.0, 1.0);
  double r   = pow (fabs (rnd), power);

  if (rnd >= 0.0) return In + Scale (r, 0.0, 1.0, 0.0, outMax - In, false);
  else            return In - Scale (r, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

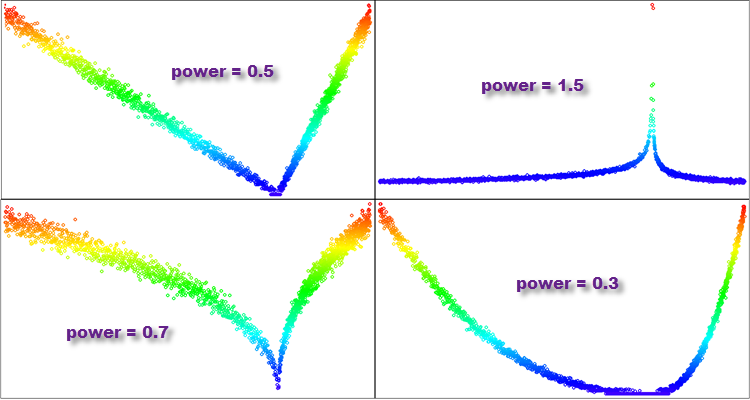
Рисунок 5. Примеры распределений функции "PowerDistribution" с различной степенью "power".

Распределение Леви (Levy distribution)

Полеты Леви - это случайные блуждания, в которых длина каждого шага определяется распределением Леви.

Распределение Леви является примером распределения с неограниченными моментами. Оно описывает случайные величины с тяжелыми хвостами, что означает, что вероятность появления очень больших значений велика. В распределении Леви моменты могут быть бесконечными или не существовать, что делает его особенным и отличающимся от распределений с ограниченными моментами, таких как нормальное распределение.

Тяжелые хвосты распределения Леви и его неограниченные моменты делают его полезным для моделирования явлений, которые могут иметь экстремальные значения или высокую вариабельность. Полеты Леви имеют множество применений в различных областях, включая физику, финансовую математику, анализ рисков, экологию, экономику и инженерию. Например, они могут использоваться для моделирования случайных процессов в физике, таких как диффузия, турбулентность и транспорт в плазме. Они также могут использоваться для моделирования поисковых стратегий животных и популяций, а также для оптимизации параметров в инженерии и финансах.

Распределение Леви было введено французским математиком Поль Леви в 1925 году и нашло множество применений в различных областях науки и техники.

Если мы говорим о приращении от конкретного значения параметра в оптимизации, то в полетах Леви каждое приращение выбирается из распределения Леви, а направление выбирается случайным образом. Это приводит к тому, что в полетах Леви некоторые шаги могут быть очень длинными, что позволяет быстрее исследовать пространство параметров, чем в случайных блужданиях с фиксированной длиной шага (приращения).

Форма распределения Полётов Леви похожа на форму степенного распределения, но в отдельных случаях бывает более эффективно использование либо одно либо другое распределение. Как и в случае со степенным законом распределения нам понадобится избавится от тяжёлых хвостов, но в данном случае мы сделаем это другим способом, для данного распределения более подходящим. Экспериментально было обнаружено, что оптимально использовать диапазон [1.0;20.0] для равномерно распределённых случайных чисел, участвующих в генерации. Нужно рассчитать минимальное значение на конце распределения для случайных чисел в степени "power", что послужит нам границей для масштабирования cгенерированного числа в диапазон [0.0;1.0].

Функция LeviDistribution принимает на вход четыре значения типа double: "in", "outMin", "outMax" и "power" и выполняет следующие шаги:

• Первым делом функция определяет минимальное значение "min" на основе параметра "power", это минимально возможное значение функции для последующего масштабирования.
  
• Затем генерируются два случайных числа "r1" и "r2" из равномерного распределения на интервалах [0.0;1.0] и [1.0;20.0] соответственно.
• Значение "y" вычисляется путем возведения "r2" в отрицательную степень "power" и масштабирования его из интервала [min, 1.0] до [0.0;1.0] с помощью функции Scale.
  
• Наконец, функция возвращает сгенерированное значение, масштабированное на интервал [outMin, outMax], в зависимости от значения "r1". Если r1 >= 0.5, то значение масштабируется на интервал [in, outMax], иначе - на интервал [outMin, in].
  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::LeviDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double min = pow (20.0, -power);
  double r1 = RNDfromCI (0.0, 1.0);
  double r2 = RNDfromCI (1.0, 20.0);
  
  double y = pow (r2, -power);
  y = Scale (y, min, 1.0, 0.0, 1.0, false);
 
  if (r1 >= 0.5) return In + Scale (y, 0.0, 1.0, 0.0, outMax - In, false);
  else           return In - Scale (y, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

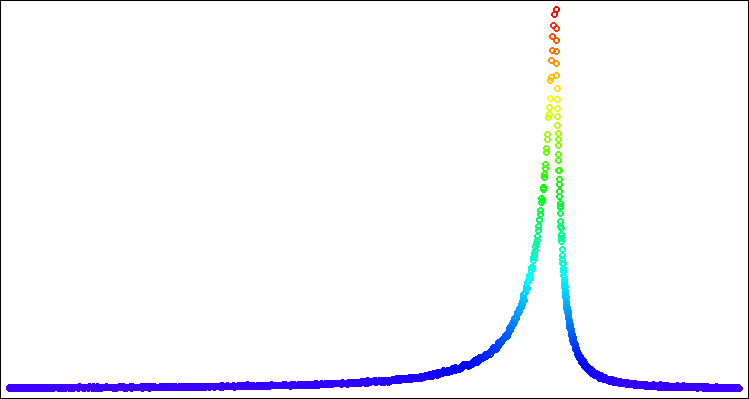
Рисунок 6. Распределение Леви с power = 1.0.

4. Шаблон для алгоритма оптимизации - Алгоритм "Умный Головастик"

Итак, переходим к самому интересному этапу нашего исследования! Проведем проверку всех распределений на специально созданном для этих целей алгоритме оптимизации под названием.... Хм, а как же мы его назовём?

Проверим идею такого алгоритма: представим себе умного головоногого, который ищет самое вкусное место, поэтому предположим, что голова его находится в эпицентре еды и что-то ест. При этом его щупальца постоянно раскидываются по сторонам в поисках новых залежей еды. Как только одна из щупалец нащупает вкусное место, голова перемещается. Возможно, это неплохая идея алгоритма, инспирированного морскими обитателями. Тогда мы знаем как его назвать - это будет Умный Головастик!

Уверен, что это будет захватывающий эксперимент, который позволит нам лучше понять, как работают различные распределения и как они могут помочь нам в решении сложных задач оптимизации. Так что давайте начнем и посмотрим, что нам удастся выяснить в этом интересном исследовании!

Логично задать свойства ног головастика соответствующим законам распределения. Тогда код ощупывания новых мест ногами головастика будет выглядеть так:

//----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double X   = 0.0;
      double in  = cB [c];
      double min = rangeMin [c];
      double max = rangeMax [c];
      
      switch (distr)
      {
      case uniformDistr: X = UniformDistribution (in, min, max);         break;
      case gaussDistr:   X = GaussDistribution   (in, min, max, powers); break;
      case powerDistr:   X = PowerDistribution   (in, min, max, powers); break;
      case leviDistr:    X = LeviDistribution    (in, min, max, powers); break;
      }

      a [i].c [c] = SeInDiSp  (X, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

Данный код представляет собой два вложенных цикла, которые проходят по каждому агенту в массиве "a" размером popSize, и для каждого элемента координаты генерируют новое значение. Генерация нового значения осуществляется путем выбора одного из четырех видов распределений и применения соответствующей функции распределения (UniformDistribution, GaussDistribution, PowerDistribution или LeviDistribution) к текущему значению "in", которое берется из массива "cB", представляющий лучшее решение на данный момент (то место, где в данный момент находится голова). Затем полученное новое значение "X" нормируется функцией SeInDiSp с использованием диапазона значений rangeMin и rangeMax и шага rangeStep для данного элемента. Полученное значение сохраняется в массиве "a" для данного агента и координаты.

Работа над этой статьёй и специфичными методами класса для генерации случайных чисел с нужными распределениями, удобными для применения в построении алгоритмов оптимизации привела к пониманию, что функция Rastrigin имеет несколько серъёзных недостатков, которые не были очевидны на момент выбора этой тестовой функции и я решил от неё отказаться. Старого доброго Rastrigin'а заменит функция Peaks (более полное обоснование будет в следующей статье).

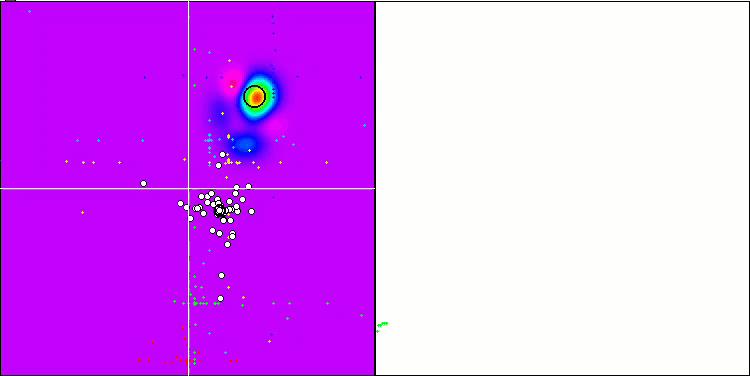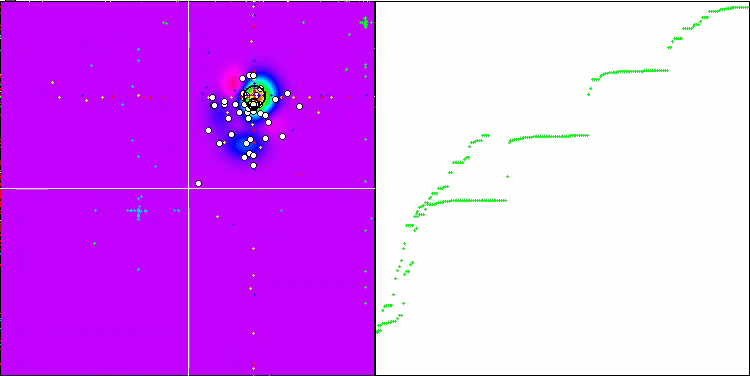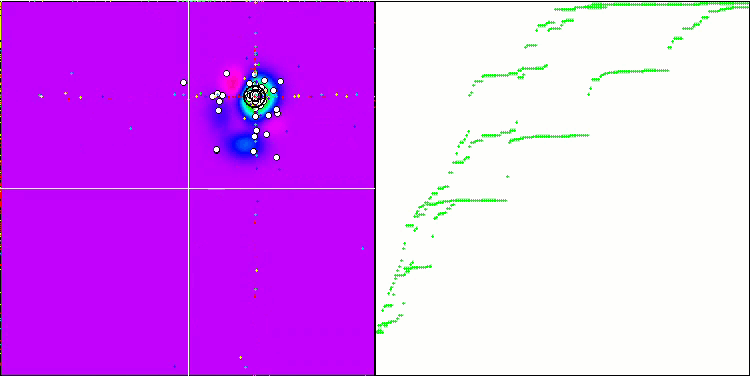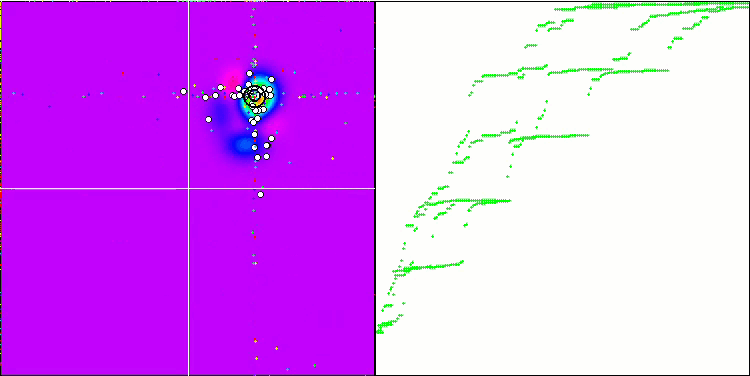
"Умный Головастик" в деле.

5. Выводы

Итак, подводя итоги, наш эксперимент с "Умным головастиком" принес интересные результаты. Анимация демонстрирует, как случайный алгоритм, применяющий определенное распределение, успешно выполняет задачу. Я не буду раскрывать, какое именно распределение и какие настройки использовались, но я предоставляю вам возможность провести свои собственные эксперименты с полным набором инструментов в этой статье. Буду рад, если вы поделитесь своими успехами в комментариях.

"Умный головастик" не будет учитываться в рейтинговой таблице, так как это просто эксперимент, который поможет нам более осознанно подходить к оптимизации.

Мои общие выводы заключаются в том, что применение распределения вероятности и выбор стратегии поиска играют важную роль в задаче оптимизации, потому что позволяет учесть стохастические факторы и более эффективно исследовать пространство решений и обнаруживать области с высокой вероятностью нахождения лучших из решений.

Однако, одного применения распределения вероятности недостаточно. Важно также учитывать выбор и особенности стратегии поиска. Различные стратегии поиска могут иметь преимущества и недостатки в зависимости от задачи оптимизации.

Поэтому, чтобы достичь еще более высоких результатов при проектировании алгоритмов оптимизации как в конкретной задаче так и в целом, необходимо совместное использование распределения вероятности и выбора стратегии поиска. Эти элементы должны работать в тандеме, чтобы обеспечить требуемые показатели разрабатываемого АО. В целом, результаты этого эксперимента подчеркивают важность осознанного подхода к оптимизации. Например, применение распределений вероятности и выбор подходящей стратегии поиска может быть полезным в области машинного обучения, где требуется оптимизация и поиск оптимальных решений.

Одна из важных особенностей представленного в этой статье инструментария заключается в возможности смещения распределений в заданном диапазоне значений. Вы не найдете возможности смещения распределения в специализированных библиотеках, ориентированных на задачи общего вида. Это позволяет исследователям управлять и настраивать распределения вероятности в соответствии с требуемыми характеристиками алгоритма оптимизации. Регулирование и контроль смещения вероятностей совместно с элементами стратегии поиска позволяют действительно творить чудеса!