MetaTrader 5 / 예
English Русский 中文 Español Deutsch 日本語 Português Français Italiano Türkçe
preview
모집단 최적화 알고리즘: 침입성 잡초 최적화(IWO)

모집단 최적화 알고리즘: 침입성 잡초 최적화(IWO)

MetaTrader 5 — 예 | 4 3월 2024, 14:19
183 0
Andrey Dik
Andrey Dik

콘텐츠

1. 소개
2. 알고리즘에 대한 설명
3. 테스트 결과


1. 소개

침입성 잡초 메타 휴리스틱 알고리즘은 잡초 군락의 호환성과 무작위성을 시뮬레이션 하여 최적화 함수의 전체 최적 값을 찾는 모집단 기반의 최적화 알고리즘입니다.
잡초 최적화 알고리즘은 자연에서 영감을 얻은 집단 알고리즘입니다. 이 알고리즘은 제한된 공간에서 제한된 시간 동안 생존을 위해 투쟁하는 잡초의 행동을 반영합니다.

잡초는 공격적인 성장력을 가지고 있으며 이로 인해 농작물에 심각한 위협이 되는 강력한 풀입니다. 또한 환경 변화에 매우 탄력적이고 적응력이 뛰어납니다. 이러한 특성을 고려하면 우리는 강력한 최적화 알고리즘을 갖추고 있는 것입니다. 이 알고리즘은 자연에 존재하는 잡초 군집의 견고성, 적응성, 무작위성을 모방합니다.

잡초가 특별한 이유는 무엇일까요? 잡초는 다양한 메커니즘을 통해 사방으로 퍼져 나가는 퍼스트 무버가 되는 경향이 있습니다. 따라서 잡초는 멸종 위기에 처한 종의 범주에 속하는 경우는 거의 없습니다.
다음은 잡초가 자연에서 적응하고 생존하는 8가지 방법에 대한 간략한 설명입니다:

1. 범용 유전자형. 이 연구를 통해 기후 변화에 따른 잡초의 진화적인 변화가 밝혀졌습니다.

2. 생애 주기 전략, 생식력. 잡초는 다양한 생애 주기 전략을 사용합니다. 경작 관리 시스템이 변화함에 따라 이전에는 특정 작물을 재배하는 시스템에서 큰 문제가 되지 않았던 잡초가 회복력을 갖게 됩니다. 예를 들어 경작 시스템이 줄어들면 다양한 생애 주기의 전략을 가진 다년생 잡초가 출현하게 됩니다. 또한 기후 변화는 변화하는 환경에 더 잘 적응하는 잡초의 종과 유전자형을 출현하게 하는 등 새로운 틈새를 만들기 시작했습니다. 이산화탄소 배출량이 증가하면 잡초는 키가 커지고 덩치가 커지며 더 강해져서 더 많은 씨앗을 생산할 수 있게 되고 공기 역학적 특성을 보면 씨앗은 키가 큰 식물에서 더 멀리 퍼질 수 있게 됩니다. 그들의 번식력은 엄청납니다. 예를 들어 옥수수 엉겅퀴는 최대 19,000개의 씨앗을 생산합니다.

3. 빠른 진화(발아, 직접적인 성장, 경쟁력, 번식 시스템, 종자 생산 및 유통 기능). 씨앗을 퍼뜨리는 능력의 증가, 수반되는 분산 및 성장은 더 많은 생존의 기회를 갖게 합니다. 잡초는 토양 조건에 많은 영향을 받지 않으며 온도와 습도의 급격한 변동에도 잘 견딥니다.

4. 후성 유전학. 많은 침입성 식물은 빠른 진화 외에도 유전자 발현을 변화시켜 변화하는 환경 요인에 빠르게 대응할 수 있는 능력을 가지고 있습니다. 끊임없이 변화하는 환경에서 식물은 빛, 온도, 물 등의 변동이나 토양 염분의 변동과 같은 스트레스를 견딜 수 있는 유연성을 갖춰야 합니다. 이를 위해 식물은 스스로 후성 유전학적인 변형을 일으킬 수 있습니다.

5. 하이브리드화. 잡종 잡초 종은 종종 이질화라고도 하는 잡종 활력을 나타냅니다. 자손은 두 부모 종에 비해 향상된 생물학적 기능을 보여줍니다. 일반적으로 잡종은 새로운 영토로 퍼져 나가고 침략한 영토 내에서 경쟁하는 능력이 향상되어 더욱 공격적으로 성장합니다.

6. 제초제에 대한 저항성 및 내성. 지난 수십 년 동안 대부분의 잡초에서 제초제에 대한 저항성이 급격히 증가했습니다.

7. 인간 활동과 관련된 잡초의 공진화. 제초제 살포 및 잡초 제거와 같은 잡초 방제 작업에서 잡초는 내성 메커니즘을 가지게 되었습니다. 잡초는 재배 식물에 비해 경작 중 외부 손상으로 인한 피해가 적습니다. 반면에 이러한 피해는 식물 번식 잡초(예: 뿌리나 뿌리줄기의 일부를 통해 번식하는 잡초)의 번식에 유용하기도 합니다.

8. 점점 더 빈번해지는 기후 변화는 잡초가 '온실' 재배 식물에 비해 더 잘 생존할 수 있는 기회를 제공합니다. 잡초는 농업에 큰 피해를 줍니다. 잡초는 재배 조건이 덜 까다롭기 때문에 성장과 발달의 측 면에서 재배 식물을 능가합니다. 수분, 영양분, 햇빛을 흡수하는 잡초는 수확량을 급격히 감소시키고 밭작물의 수확과 탈곡을 어렵게 만들며 제품의 품질을 악화시킵니다.

2. 알고리즘에 대한 설명

침입성 잡초 알고리즘은 자연에서 잡초가 자라는 과정에서 영감을 얻었습니다. 이 메서드는 2006년에 메라비안과 루카스에 의해 도입되었습니다. 당연히 잡초가 무성하게 자랐고, 이 무성한 성장은 유용한 식물에 심각한 위협이 됩니다. 잡초의 중요한 특성은 이들의 자연에서의 저항성과 높은 적응력이며 이는 IWO 알고리즘을 최적화하는 기반이 됩니다. 이 알고리즘은 효율적인 최적화 접근법의 기초로 사용될 수 있습니다.

IWO는 잡초의 군집 행동을 모방한 연속 확률적 수치 알고리즘입니다. 먼저 초기 시드 모집단이 전체 검색 공간에 무작위로 배포됩니다. 이 잡초는 자라나게 되고 알고리즘의 다음 단계를 수행하게 됩니다. 알고리즘은 의사 코드로 표현할 수 있는 7단계로 구성됩니다:

1. 무작위로 씨앗 뿌리기
2. FF 계산
3. 잡초에서 씨앗 뿌리기
4. FF 계산
5. 자식 잡초를 부모 잡초와 병합
6. 모든 잡초 분류
7. 7) 정지 조건이 충족될 때까지 3단계부터 반복합니다.

블록 다이어그램은 한 번의 반복에서 알고리즘의 작동을 나타냅니다. IWO는 시드 초기화 프로세스로 작업을 시작합니다. 씨앗은 검색 공간의 '필드'에 무작위로 균일하게 흩어져 있습니다. 그 후 우리는 씨앗이 발아하여 성인 식물을 형성했다고 가정하며 이는 피트니스 기능에 의해 평가되어야 합니다.

다음 단계에서는 각 식물의 체력을 알면 우리는 잡초가 씨앗을 통해 번식하도록 허용할 수 있습니다. 이때 씨앗의 수는 체력에 비례합니다. 그 후 발아한 씨앗을 모 식물과 결합하여 분류합니다. 일반적으로 침입성 잡초 알고리즘은 다른 애플리케이션과 함께 코딩, 수정 및 사용하기가 간단하다고 볼 수 있습니다.

계획

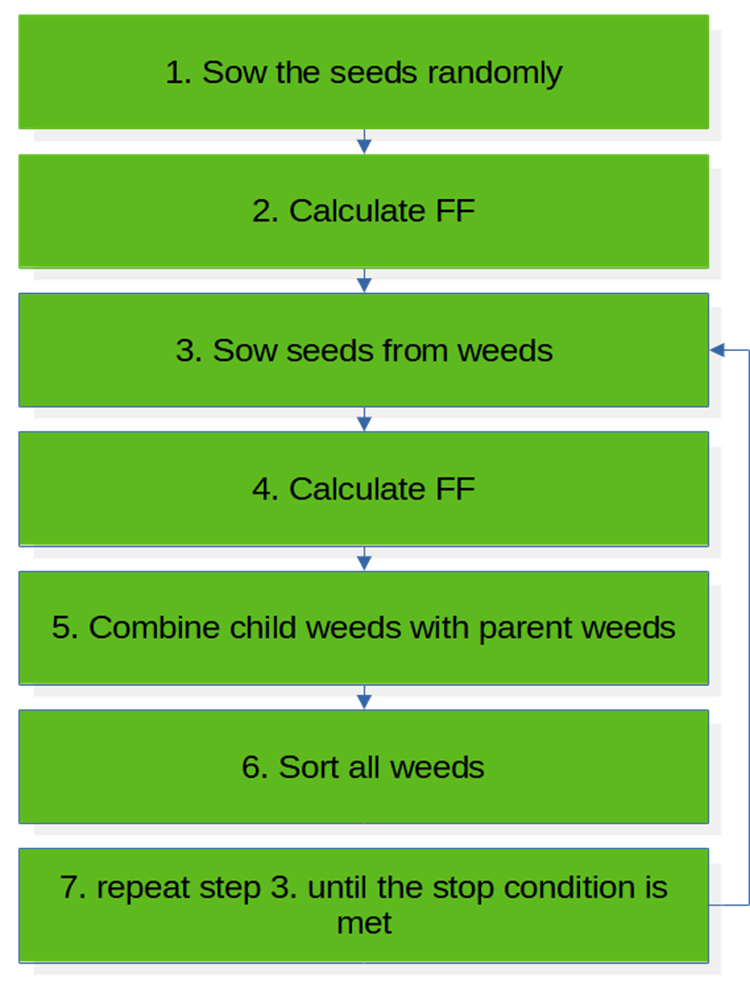
그림 1. BA 알고리즘 블록 다이어그램

이제 잡초 알고리즘의 기능에 대해 살펴보겠습니다. 이 알고리즘은 잡초가 가진 극한의 생존 능력을 다수 갖추고 있습니다. 잡초 군집의 특징은 유전자, 꿀벌 및 기타 알고리즘과 달리 군집의 모든 식물이 예외 없이 씨앗을 파종한다는 것입니다. 최악의 적응 식물이 지구의 극한에 가장 근접할 수 있는 확률은 항상 0이 아니기 때문에 최악의 적응 식물도 후손을 남길 수 있습니다.

제가 이미 말했듯이 각 잡초는 가능한 최소량에서 가능한 최대량 (알고리즘의 외부 매개 변수) 범위 내에서 씨앗을 생산합니다. 당연히 이러한 조건에서는 각 식물이 하나 이상의 씨앗을 남기게 되면 부모 식물보다 자식 식물이 더 많아지는데 이 기능은 코드에서 흥미롭게도 구현되어 있습니다. 이에 대해서는 아래에서 설명할 것입니다. 일반적인 알고리즘은 그림 2에 시각적으로 표시되어 있습니다. 부모 식물은 체력에 비례하여 씨앗을 뿌립니다.

그래서 1번 식물은 6개의 씨앗을 뿌렸고, 6번 식물은 단 하나의 씨앗(보장된 씨앗)만 뿌렸습니다. 발아한 씨앗은 이후 부모 식물과 함께 분류된 식물을 생산합니다. 이것은 생존의 모방입니다. 정렬된 전체 그룹에서 새로운 부모 식물이 선택되고 다음 반복에서 라이프사이클이 반복됩니다. 이 알고리즘은 '인구 과잉'과 종자 파종 능력의 불완전한 실현이라는 문제를 해결하는 메커니즘을 갖추고 있습니다.

예를 들어 알고리즘의 매개 변수 중 하나인 씨앗 수가 50개이고 부모 식물의 수가 5개, 최소 씨앗 수는 1개, 최대 씨앗 수는 6개인 경우를 가정해 보겠습니다. 이 경우 5 * 6 = 30으로 50보다 작습니다. 이 예에서 볼 수 있듯이 파종의 가능성은 완전히 실현되지 않았습니다. 이 경우 모든 부모 식물에서 허용되는 최대 자손 수에 도달할 때까지 자손을 유지할 수 있는 권한이 목록의 다음 부모 식물에게 넘어갑니다. 목록의 끝에 도달하면 오른쪽은 목록의 첫 번째 항목으로 이동하고 한도를 초과하는 자손을 남길 수 있습니다. 

IWO

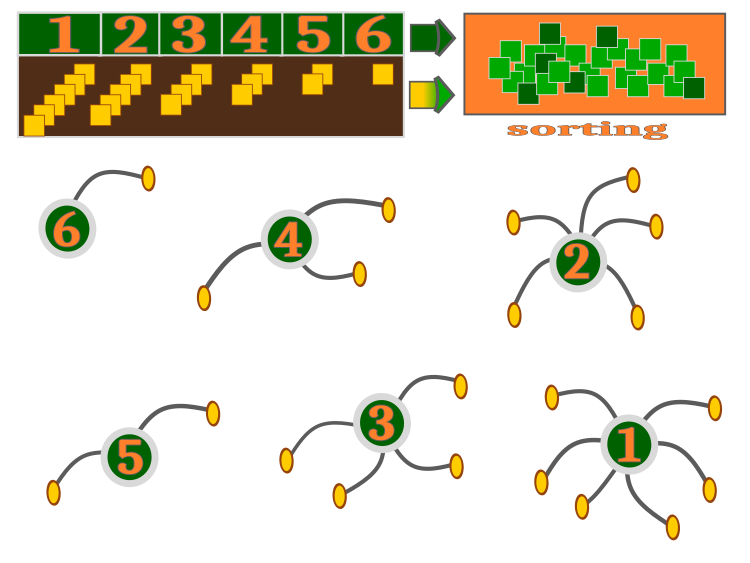
그림 2. IWO 알고리즘 작동. 자손의 수는 부모의 체력에 비례합니다.

다음으로 주의해야 할 것은 씨앗 뿌리기 분산 입니다. 알고리즘의 씨앗 뿌리기 분산은 반복 횟수에 비례하는 선형 감소 함수입니다. 외부의 분산 매개변수는 씨앗 살포의 하한과 상한입니다. 따라서 반복 횟수가 증가함에 따라 시딩 반경이 감소하고 발견된 극한값이 세분화됩니다. 알고리즘 개발자의 권고에 따르면 정규 시딩 분포를 적용해야 하지만 저는 계산을 단순화하여 3차 함수를 적용했습니다. 반복 횟수의 분산 함수는 그림 3에서 확인할 수 있습니다.

disp

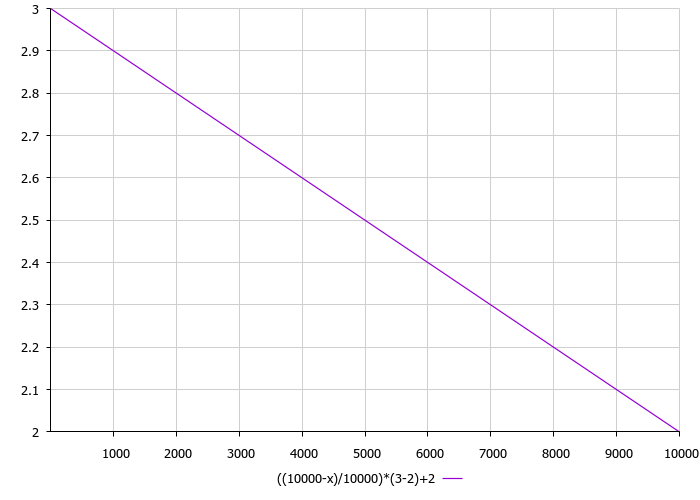
그림 3. 반복 횟수에 대한 분산의 종속성은 여기서 3이 최대 한도이고 2는 최소 한도입니다.

이제 IWO 코드로 넘어가 보겠습니다. 코드는 간단하고 실행 속도가 빠릅니다.

알고리즘의 가장 간단한 단위(에이전트)는 '잡초'입니다. 잡초는 잡초의 씨앗과도 연관이 있습니다. 이렇게 하면 우리는 이후 발생하는 정렬에 동일한 유형의 데이터를 사용할 수 있습니다. 구조는 좌표 배열, 적합도 함수 값을 저장하는 변수, 씨앗(자손)의 수를 나타내는 카운터로 구성됩니다. 우리는 이 카운터를 통해 각 식물에 허용되는 최소 및 최대 씨앗 수를 제어할 수 있습니다. 

//——————————————————————————————————————————————————————————————————————————————
struct S_Weed
{
  double c []; //coordinates
  double f;    //fitness
  int    s;    //number of seeds
};
//——————————————————————————————————————————————————————————————————————————————

우리에게는 체력에 비례하여 부모를 선택하는 확률 함수를 구현하는 구조가 필요할 것입니다. 이 경우 꿀벌 군집 알고리즘에서 이미 살펴본 룰렛 원리가 적용됩니다. 'start' 및 'end' 변수는 확률 필드의 시작과 끝을 담당합니다.

//——————————————————————————————————————————————————————————————————————————————
struct S_WeedFitness
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

이제 잡초 알고리즘의 클래스를 선언해 보겠습니다. 그 안에 최적화할 매개변수의 경계와 단계, 잡초를 설명하는 배열, 씨앗 배열, 최적의 전역 좌표 배열, 알고리즘이 달성한 적합도 함수의 최적값 등 필요한 모든 변수를 선언합니다. 또한 첫 번째 반복의 '파종' 플래그와 알고리즘 매개변수의 상수 변수도 필요합니다.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_IWO
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Weed weeds     []; //weeds
  public: S_Weed weedsT    []; //temp weeds
  public: S_Weed seeds     []; //seeds
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP);    //Maximum iterations

  public: void Sowing      (int iter);
  public: void Germination ();

  //============================================================================
  private: void   Sorting        ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];            //Vector
  private: int    ind [];
  private: double val [];
  private: S_WeedFitness wf [];      //Weed fitness
  private: bool   sowing;            //Sowing
  private: int    coordinates;       //Coordinates number
  private: int    numberSeeds;       //Number of seeds
  private: int    numberWeeds;       //Number of weeds
  private: int    totalNumWeeds;     //Total number of weeds
  private: int    maxNumberSeeds;    //Maximum number of seeds
  private: int    minNumberSeeds;    //Minimum number of seeds
  private: double maxDispersion;     //Maximum dispersion
  private: double minDispersion;     //Minimum dispersion
  private: int    maxIteration;      //Maximum iterations
};
//——————————————————————————————————————————————————————————————————————————————

초기화 함수의 개방형 메서드에서 상수 변수에 값을 할당하고 알고리즘의 입력 매개 변수에 유효한 값이 있는지 확인하여 최소 씨앗 값과 부모 식물의 곱이 가능한 총 씨앗 수를 초과할 수 없도록 합니다. 정렬을 수행할 배열을 결정하려면 부모 식물과 씨앗의 합계가 필요합니다. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP)     //Maximum iterations
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberSeeds    = numberSeedsP;
  numberWeeds    = numberWeedsP;
  maxNumberSeeds = maxNumberSeedsP;
  minNumberSeeds = minNumberSeedsP;
  maxDispersion  = maxDispersionP;
  minDispersion  = minDispersionP;
  maxIteration   = maxIterationP;


  if (minNumberSeeds < 1) minNumberSeeds = 1;
  if (numberWeeds * minNumberSeeds > numberSeeds) numberWeeds = numberSeeds / minNumberSeeds;
  else numberWeeds = numberWeedsP;

  totalNumWeeds  = numberWeeds + numberSeeds;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (weeds,  totalNumWeeds);
  ArrayResize (weedsT, totalNumWeeds);
  ArrayResize (seeds,  numberSeeds);

  for (int i = 0; i < numberWeeds; i++)
  {
    ArrayResize (weeds  [i].c, coordinates);
    ArrayResize (weedsT [i].c, coordinates);
    weeds [i].f = -DBL_MAX;
    weeds [i].s = 0;
  }
  for (int i = 0; i < numberSeeds; i++)
  {
    ArrayResize (seeds [i].c, coordinates);
    seeds [i].s = 0;
  }

  ArrayResize (ind, totalNumWeeds);
  ArrayResize (val, totalNumWeeds);

  ArrayResize (wf, numberWeeds);
}
//——————————————————————————————————————————————————————————————————————————————

이제 각 반복에서 호출되는 첫 번째 공용 메서드인 Flight()를 살펴보겠습니다. 알고리즘의 주요 로직은 다음과 같습니다. 여러분이 이해하기 쉽도록 메서드를 여러 부분으로 나누겠습니다.

알고리즘이 첫 번째 반복에 있을 때는 검색 공간 전체에 씨앗을 뿌려야 합니다. 이 작업은 일반적으로 무작위로 균등하게 수행됩니다. 최적화된 매개변수의 허용 가능한 값 범위에서 난수를 생성한 후 획득한 값이 범위를 벗어나는지 여부를 확인하고 알고리즘 매개변수들로 정의된 불연속성을 설정합니다. 여기에서는 나중에 코드에서 씨앗을 뿌릴 때 필요한 분포 벡터도 할당합니다. 씨앗 적합성의 값을 최소한의 더블 값으로 초기화하고 씨앗 카운터를 초기화합니다(씨앗은 식물이 될 것이고 씨앗 카운터를 사용할 것입니다).

//the first sowing of seeds---------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;

  for (int s = 0; s < numberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      seeds [s].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      vec [c] = rangeMax [c] - rangeMin [c];
    }

    seeds [s].f = -DBL_MAX;
    seeds [s].s = 0;
  }

  sowing = true;
  return;
}

코드의 이 섹션에서는 현재 반복에 따라 분산이 계산됩니다. 앞서 말씀드린 각 부모 잡초에 대한 보장된 최소 씨앗 수가 여기에 구현되어 있습니다. 최소 씨앗 수 보장은 두 개의 루프를 통해 제공되며 첫 번째 루프에서는 부모 식물을 분류하고 두 번째 루프에서는 실제로 새로운 씨앗을 생성하면서 씨앗 카운터를 늘립니다. 보시다시피 새로운 자손을 생성한다는 것은 이전에 계산된 분산을 가진 3차 함수의 분포로 난수를 부모 좌표로 증가시키는 것을 말합니다. 얻어진 새로운 좌표의 값이 허용 가능한 값인지 확인하고 이산성을 지정합니다.

//guaranteed sowing of seeds by each weed-------------------------------------
int    pos = 0;
double r   = 0.0;
double dispersion = ((maxIteration - iter) / (double)maxIteration) * (maxDispersion - minDispersion) + minDispersion;

for (int w = 0; w < numberWeeds; w++)
{
  weeds [w].s = 0;

  for (int s = 0; s < minNumberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      r = RNDfromCI (-1.0, 1.0);
      r = r * r * r;

      seeds [pos].c [c] = weeds [w].c [c] + r * vec [c] * dispersion;
      seeds [pos].c [c] = SeInDiSp (seeds [pos].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    pos++;
    weeds [w].s++;
  }
}

이 코드를 사용하여 우리는 룰렛 원리에 따라 적합도에 비례하여 각 부모 식물에 대한 확률 필드를 제공합니다. 위의 코드는 각 식물에 대해 보장된 씨앗 수를 제공했는데 여기서 씨앗 수는 무작위 법칙을 따르기 때문에 잡초가 더 많이 적응할수록 더 많은 씨앗을 남길 수 있고 그 반대의 경우도 마찬가지입니다. 식물이 덜 적응할수록 식물은 씨앗을 덜 생산합니다.

//============================================================================
//sowing seeds in proportion to the fitness of weeds--------------------------

//the distribution of the probability field is proportional to the fitness of weeds
wf [0].start = weeds [0].f;
wf [0].end   = wf [0].start + (weeds [0].f - weeds [numberWeeds - 1].f);

for (int f = 1; f < numberWeeds; f++)
{
  if (f != numberWeeds - 1)
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f].f - weeds [numberWeeds - 1].f);
  }
  else
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f - 1].f - weeds [f].f) * 0.1;
  }
}

우리는 획득한 확률 필드를 기반으로 자손을 남길 권리가 있는 부모 식물을 선택합니다. 시드 카운터가 허용된 최대 값에 도달하면 정렬된 목록에서 오른쪽이 다음으로 넘어갑니다. 목록의 끝에 도달하면 오른쪽이 다음 항목으로 넘어가지 않고 목록의 첫 번째 항목으로 이동합니다. 그런 다음 계산된 분산으로 위에서 설명한 규칙에 따라 딸 식물이 형성됩니다.

bool seedingLimit = false;
int  weedsPos = 0;

for (int s = pos; s < numberSeeds; s++)
{
  r = RNDfromCI (wf [0].start, wf [numberWeeds - 1].end);

  for (int f = 0; f < numberWeeds; f++)
  {
    if (wf [f].start <= r && r < wf [f].end)
    {       
      weedsPos = f;
      break;
    }
  }

  if (weeds [weedsPos].s >= maxNumberSeeds)
  {
    seedingLimit = false;
    while (!seedingLimit)
    {
      weedsPos++;
      if (weedsPos >= numberWeeds)
      {
        weedsPos = 0;
        seedingLimit = true;
      }
      else
      {
        if (weeds [weedsPos].s < maxNumberSeeds)
        {
          seedingLimit = true;
        }
      }
    }
  }

  for (int c = 0; c < coordinates; c++)
  {
    r = RNDfromCI (-1.0, 1.0);
    r = r * r * r;

    seeds [s].c [c] = weeds [weedsPos].c [c] + r * vec [c] * dispersion;
    seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  seeds [s].s = 0;
  weeds [weedsPos].s++;
}

두 번째 오픈 메서드는 각 반복마다 실행해야 하며 각 하위 잡초에 대한 적합성 함수를 계산한 후에 필요합니다. 정렬을 적용하기 전에 발아한 씨앗을 목록 끝에 있는 부모 식물과 함께 공통 배열에 배치하여 이전 반복에서 자손과 부모를 모두 포함할 수 있는 이전 세대를 대체합니다. 따라서 우리는 자연에서 일어나는 것과 마찬가지로 약하게 적응한 잡초를 없애 버립니다. 그런 다음 정렬을 적용합니다. 결과 목록의 첫 번째 잡초는 정말 더 나은 솔루션이라면 글로벌로 최상의 솔루션으로 업데이트할 가치가 있습니다. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Germination ()
{
  for (int s = 0; s < numberSeeds; s++)
  {
    weeds [numberWeeds + s] = seeds [s];
  }

  Sorting ();

  if (weeds [0].f > fB) fB = weeds [0].f;
}
//——————————————————————————————————————————————————————————————————————————————


3. 테스트 결과

테스트 스탠드 결과는 다음과 같습니다:

2023.01.13 18:12:29.880 Test_AO_IWO (EURUSD,M1) C_AO_IWO:50;12;5;2;0.2;0.01
2023.01.13 18:12:29.880    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:12:32.251 Test_AO_IWO (EURUSD,M1) 5 Rastrigin's; Func 실행 10000 결과: 79.71791976868334
2023.01.13 18:12:32.251    Test_AO_IWO (EURUSD,M1)    Score: 0.98775
2023.01.13 18:12:36.564 Test_AO_IWO (EURUSD,M1) 25 Rastrigin's; Func 실행 10000 결과: 66.60305588198622
2023.01.13 18:12:36.564    Test_AO_IWO (EURUSD,M1)    Score: 0.82525
2023.01.13 18:13:14.024 Test_AO_IWO (EURUSD,M1) 500 Rastrigin's; Func 실행 10000 결과: 45.4191288396659
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    Score: 0.56277
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    5 Forest's; Func runs 10000 result: 1.302934874807614
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    Score: 0.73701
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    25 Forest's; Func 10000 실행 결과: 0.5630336066477166
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    Score: 0.31848
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.11082098547471195
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    Score: 0.06269
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 6.640000000000001
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    Score: 0.55333
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 2.6
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    Score: 0.21667
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.5668
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    Score: 0.04723

한눈에 보기만 해도 테스트 함수들에서 알고리즘의 높은 결과를 확인할 수 있습니다. 지금까지 고려된 알고리즘 중 평활 함수보다 이산 함수에서 더 나은 수렴을 보인 알고리즘은 없었지만 모든 알고리즘에서 예외 없이 숲 및 메가시티 함수의 복잡성으로 설명되는 평활 함수 작업에 대한 선호도가 눈에 띄게 높습니다. 언젠가는 평활 함수보다 이산 함수를 더 잘 풀 수 있는 테스트용 알고리즘이 나올 수도 있습니다.


rastrigin

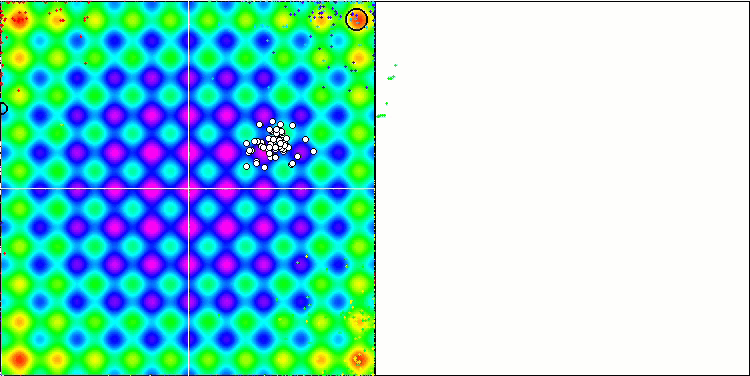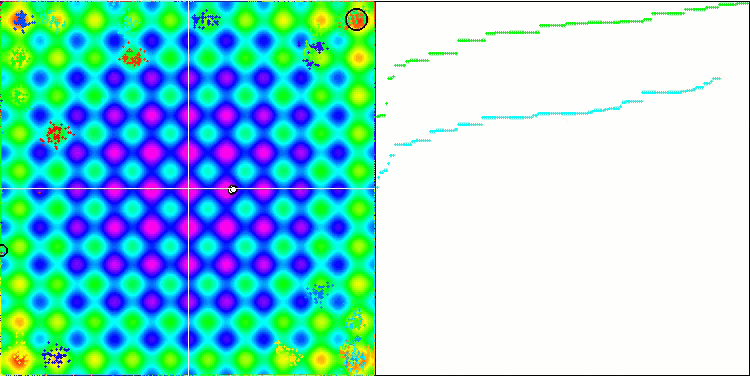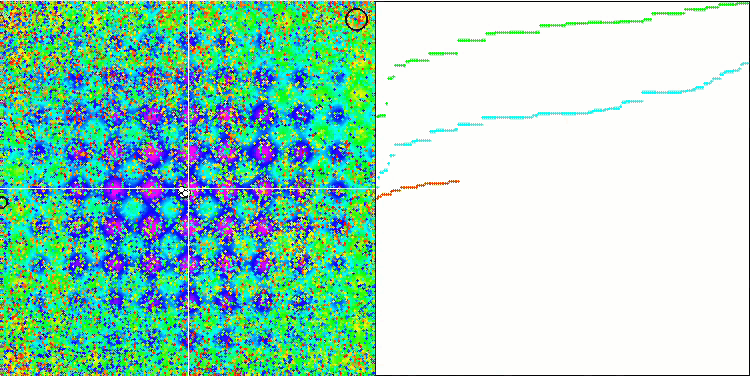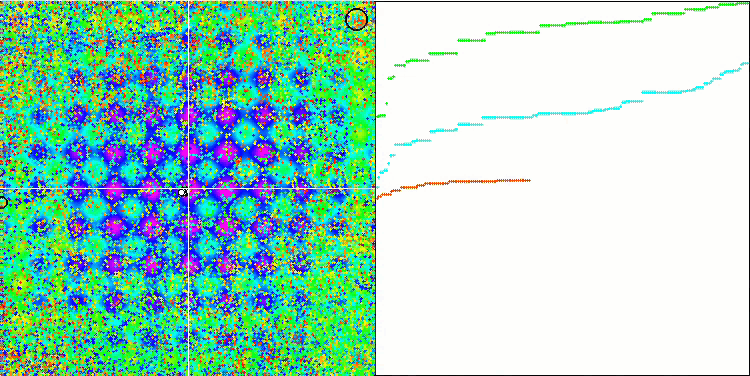
  rastrigin 테스트 함수에서 IWO

숲

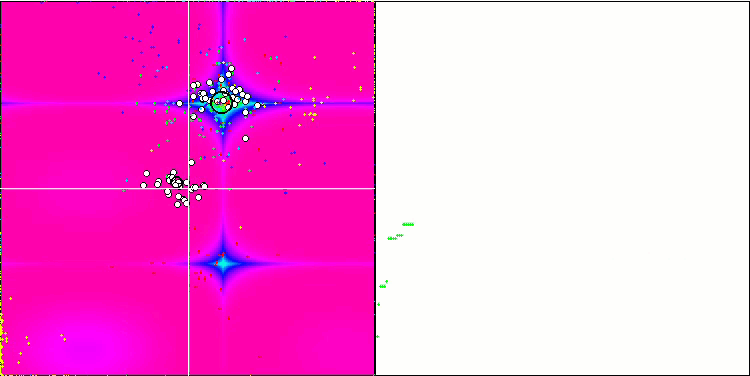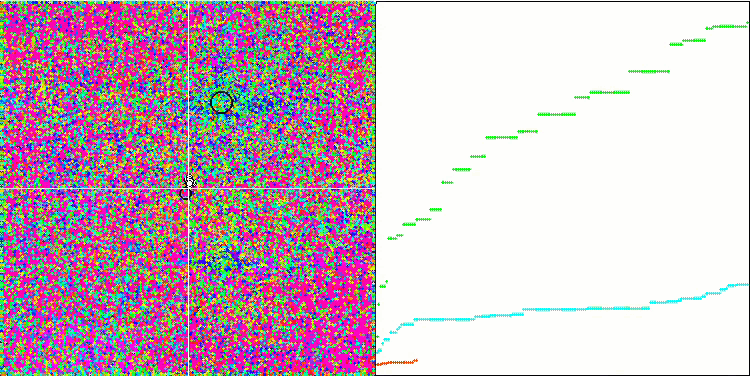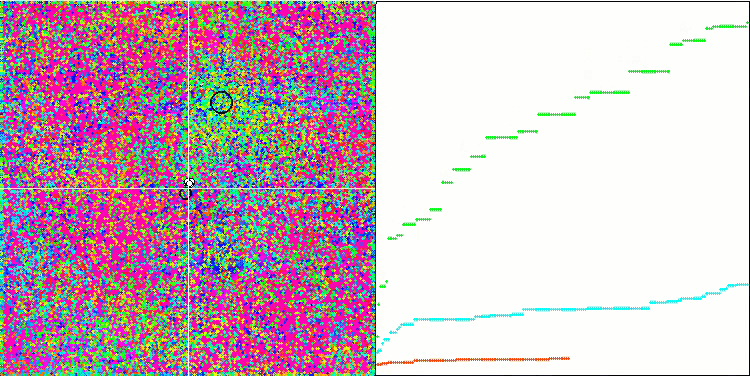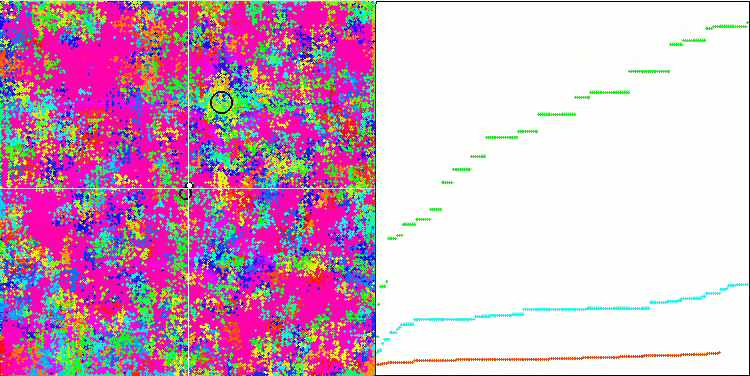
IWO 숲 테스트 함수에서

메가

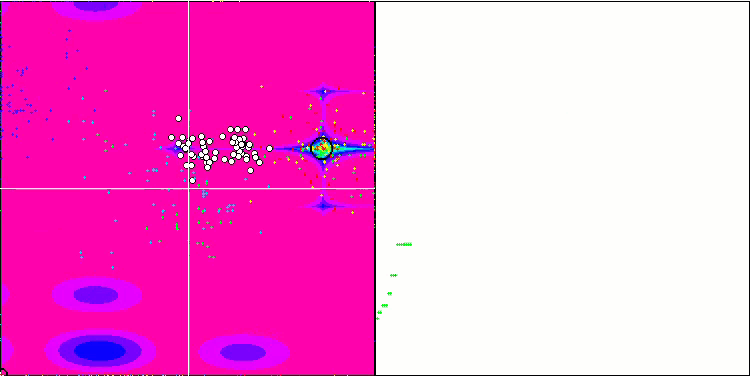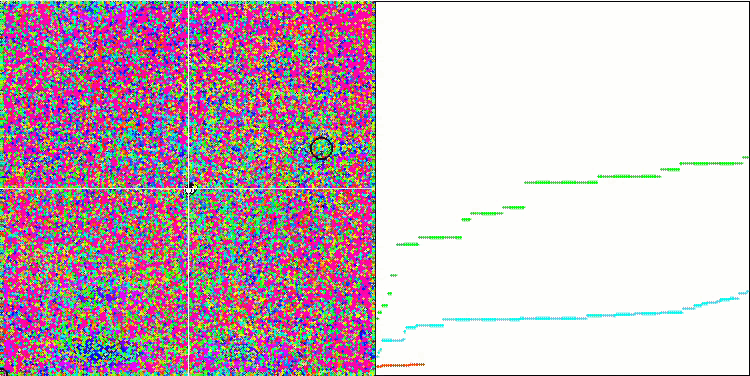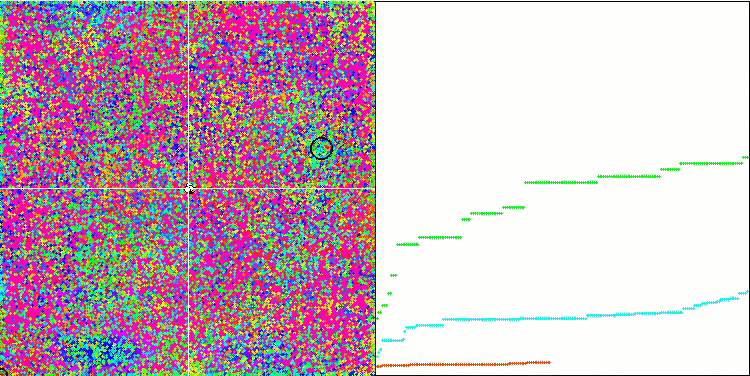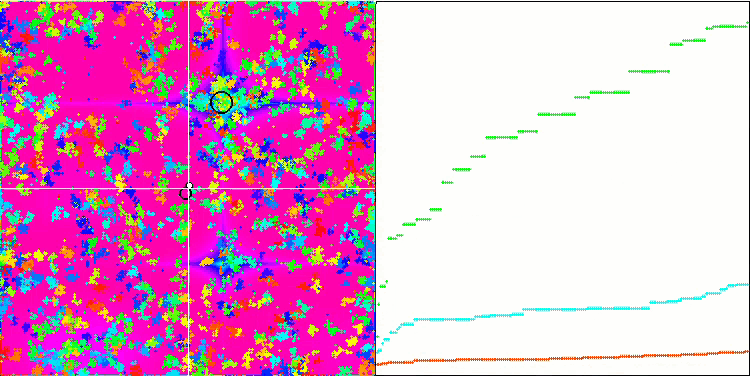
메가시티 테스트 함수에서 IWO

침입성 잡초 알고리즘은 대부분의 테스트에서 인상적인 결과를 보였는데 특히 매개변수가 10개와 50개인 평활 Rastrigin 함수에서 두드러졌습니다. 1000개의 매개 변수를 사용한 테스트에서만 성능이 약간 떨어졌는데 이는 일반적으로 평활 함수에서 좋은 성능일 것을 나타냅니다. 이는 우리로 하여금 복잡한 평활 함수 및 신경망에 대한 알고리즘을 예상할 수 있도록 해 줍니다. 숲 기능의 경우 알고리즘은 10개의 매개변수를 사용한 첫 번째 테스트에서 좋은 결과를 보였지만 여전히 전체적으로는 평균적인 결과를 보여주었습니다. 메가시티 이산 함수에서 침입 잡초 알고리즘은 평균 이상의 성능을 보였으며 특히 1000개의 변수를 사용한 테스트에서 뛰어난 확장성을 보였고 반딧불 알고리즘에게만 1위를 내줬지만 10개와 50개의 변수를 사용한 테스트에서는 크게 앞서는 성능을 보였습니다.

침입성 잡초 알고리즘에는 상당히 많은 수의 매개변수가 있지만 매개변수가 매우 직관적이고 이 매개 변수들을 쉽게 구성할 수 있기 때문에 이를 단점으로 간주해서는 안 됩니다. 또한 알고리즘의 미세 조정은 일반적으로 이산 함수의 테스트 결과에만 영향을 미치며 평활 함수에 대한 결과는 양호한 상태를 유지합니다.

테스트 함수의 시각화에서 우리는 검색 공간의 특정 부분을 분리하고 탐색하는 알고리즘의 기능을 명확하게 볼 수 있습니다. 이는 꿀벌 알고리즘과 다른 알고리즘에서도 마찬가지였습니다. 반면에 여러 책에서는 이 알고리즘이 자주 멈추는 경향이 있고 검색 기능이 약하다고 지적합니다. 알고리즘에 글로벌 극한값에 대한 참조가 없고 로컬 함정에서 '점프'하는 메커니즘이 없음에도 불구하고 IWO는 숲과 메가시티와 같은 복잡한 함수에서 어떻게든 적절하게 작동합니다. 이산 함수로 작업하는 동안 매개변수가 최적화될수록 결과가 더 안정적으로 됩니다.

각 반복에 따라 시드 분산이 선형적으로 감소하기 때문에 최적화가 끝날수록 극한값의 세분화가 더욱 증가합니다. 제 생각에는 이것이 최적이라고 보이지는 않습니다 왜냐하면 알고리즘의 탐색 기능이 시간이 지남에 따라 고르지 않게 분배되고 우리는 테스트 함수가 일정한 백색 소음으로 시각화 될 때 알 수 있기 때문입니다. 또한 이러한 검색의 불균일성은 테스트 스탠드 창의 오른쪽에 있는 수렴 그래프로 판단할 수 있습니다. 최적화를 시작할 때 수렴이 가속화하는 것이 가끔 관찰되는데 이는 거의 모든 알고리즘에서 나타나는 일반적인 현상입니다. 수렴이 급격이 시작된 후에는 대부분의 최적화 과정에서 수렴 속도가 느려집니다. 마지막에 가까워질수록 수렴이 크게 가속화 되는 것을 볼 수 있습니다. 분산도의 동적 변화는 더 자세한 연구와 실험이 필요한 이유입니다. 왜냐하면 반복 횟수가 더 많으면 우리는 수렴이 다시 시작될 수 있음을 알 수 있기 때문입니다. 그러나 객관성과 실질적인 타당성을 유지하기 위해 실시하는 비교 테스트에는 한계가 있습니다. 

이제 최종 평점 표로 이동하겠습니다. 표를 보면 현재 IWO가 선두에 있다는 것을 알 수 있습니다. 이 알고리즘은 9개의 테스트 중 2개의 테스트에서 가장 좋은 결과를 보였고 나머지 테스트에서는 평균보다 훨씬 나은 결과를 보였으므로 최종 결과는 100점입니다. 수정된 개미 군집 알고리즘(ACOm)이 2위를 차지했습니다. 개미 군집 알고리즘은 9개 테스트 중 5개 테스트에서 최고를 유지했습니다.

AO

설명

라스트리진

라스트리진 최종

숲

숲 최종

메가시티(이산)

메가시티 최종

최종 결과

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

IWO

침입성 잡초 최적화

1.00000

1.00000

0.33519

2.33519

0.79937

0.46349

0.41071

1.67357

0.75912

0.44903

0.94088

2.14903

100.000

ACOm

개미 식민지 최적화 M

0.36118

0.26810

0.17991

0.80919

1.00000

1.00000

1.00000

3.00000

1.00000

1.00000

0.10959

2.10959

95.996

COAm

뻐꾸기 최적화 알고리즘 M

0.96423

0.69756

0.28892

1.95071

0.64504

0.34034

0.21362

1.19900

0.67153

0.34273

0.45422

1.46848

74.204

FAm

반딧불이 알고리즘 M

0.62430

0.50653

0.18102

1.31185

0.55408

0.42299

0.64360

1.62067

0.21167

0.28416

1.00000

1.49583

71.024

BA

박쥐 알고리즘

0.42290

0.95047

1.00000

2.37337

0.17768

0.17477

0.33595

0.68840

0.15329

0.07158

0.46287

0.68774

59.650

ABC

인공 꿀벌 군집

0.81573

0.48767

0.22588

1.52928

0.58850

0.21455

0.17249

0.97554

0.47444

0.26681

0.35941

1.10066

57.237

FSS

물고기 떼 검색

0.48850

0.37769

0.11006

0.97625

0.07806

0.05013

0.08423

0.21242

0.00000

0.01084

0.18998

0.20082

20.109

PSO

파티클 스웜 최적화

0.21339

0.12224

0.05966

0.39529

0.15345

0.10486

0.28099

0.53930

0.08028

0.02385

0.00000

0.10413

14.232

RND

랜덤

0.17559

0.14524

0.07011

0.39094

0.08623

0.04810

0.06094

0.19527

0.00000

0.00000

0.08904

0.08904

8.142

GWO

회색 늑대 최적화

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.18977

0.04119

0.01802

0.24898

1.000


침입성 위드 알고리즘은 글로벌 검색에 적합합니다. 이 알고리즘은 좋은 성능을 보이지만 모집단의 최상위 멤버가 사용되지는 않습니다. 그리고 국부적 극단에서 잠재적인 고착화를 방지하는 메커니즘이 없습니다. 알고리즘의 연구와 활용 사이에 균형은 없지만 이것이 알고리즘의 정확성과 속도에 부정적인 영향을 미치지는 않았습니다. 이 알고리즘에는 다른 단점도 있습니다. 최적화 전반에 걸쳐 검색 성능이 고르지 않다는 사실은 위에서 언급한 문제를 해결할 수 있다면 IWO의 성능이 잠재적으로 더 높아질 수 있음을 의미합니다.

그림 4의 알고리즘 테스트 결과 히스토그램

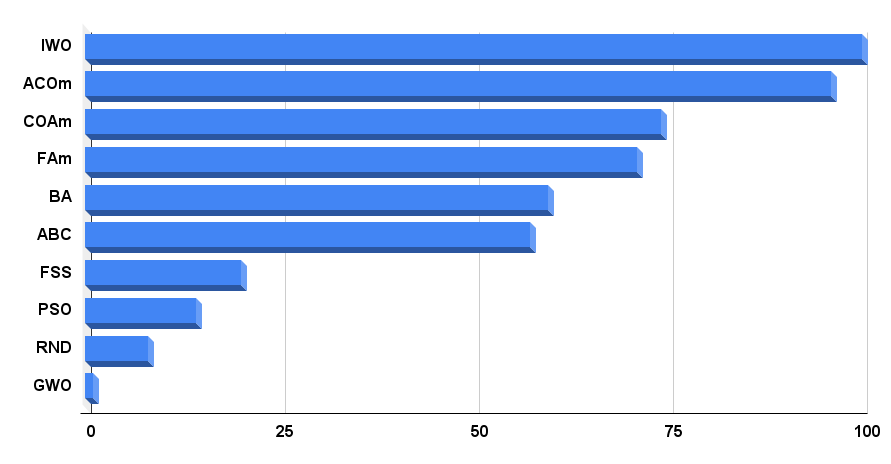
그림 4. 테스트 알고리즘의 최종 결과 히스토그램

침입형 잡초 최적화(IWO) 알고리즘의 속성에 대한 결론:

장점:
1. 빠른 속도.
2. 이 알고리즘은 평활하고 불 연속적인 다양한 유형의 함수에 잘 작동합니다.
3. 우수한 확장성

단점:
1. 수많은 매개변수(설명이 필요 없지만)가 있습니다.


MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/11990

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기
프랙탈로 트레이딩 시스템 설계하는 방법 알아보기 프랙탈로 트레이딩 시스템 설계하는 방법 알아보기
이 글은 가장 인기 있는 보조지표를 기반으로 트레이딩 시스템을 설계하는 방법에 대한 시리즈의 새로운 글입니다. 우리는 프랙탈 지표인 새로운 지표에 대해 배우고 이를 기반으로 MetaTrader 5 터미널에서 실행될 거래 시스템을 설계하는 방법을 알아볼 것입니다.
클래스에서 ONNX 모델 래핑하기 클래스에서 ONNX 모델 래핑하기
객체 지향 프로그래밍을 사용하면 읽기 쉽고 수정하기 쉬운 보다 간결한 코드를 작성할 수 있습니다. 여기서는 세개의 ONNX 모델에 대한 예제를 살펴보겠습니다.
Expert Advisor 개발 기초부터(26부): 미래를 향해(I) Expert Advisor 개발 기초부터(26부): 미래를 향해(I)
오늘은 주문 시스템을 한 단계 더 발전시켜 보겠습니다. 하지만 그 전에 우리는 몇 가지 문제를 해결해야 합니다. 우리가 어떻게 하고 싶은지, 거래일 동안 우리가 어떤 일을 할 것인지와 관련된 몇 가지 질문이 있습니다.
Expert Advisor 개발 기초부터(25부): 시스템 견고성 확보(II) Expert Advisor 개발 기초부터(25부): 시스템 견고성 확보(II)
이 글에서는 EA의 성능을 향상하기 위한 마지막 단계를 밟아보겠습니다. 그러니 오랫동안 읽을 준비를 하세요. Expert Advisor의 신뢰성을 높이기 위해 우리는 코드에서 모든 것을 제거합니다. 이 코드는 거래 시스템의 일부가 아닌 코드입니다.