Algoritmos de optimización de la población: Algoritmo de luciérnagas (Firefly Algorithm - FA)

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas

1. Introducción

La naturaleza ha sido, es y será una fuente de inspiración para muchos algoritmos metaheurísticos, pues siempre se las arregla para hallar soluciones a los problemas sin valerse de ninguna pista, simplemente usando la experiencia individual como base. La selección natural y la supervivencia del más apto fueron la principal motivación para crear los primeros algoritmos metaheurísticos. En la naturaleza, los animales se comunican entre sí de muchas maneras. Las luciérnagas usan para comunicarse su habilidad para destellar. Existen alrededor de 2000 especies de luciérnagas con sus propios patrones de destellos característicos. Normalmente, suelen producir un breve destello con un patrón específico. En este caso, la luz y su intensidad se convierten en el resultado de procesos bioquímicos conocidos como bioluminiscencia. Se cree que la función principal de dichos destellos es atraer a especímenes del sexo opuesto y posibles presas. Algunas luciérnagas tropicales pueden sincronizar sus destellos, mostrando así un ejemplo de autoorganización biológica. La intensidad de la luz, en función de la distancia desde su fuente, obedece a la ley del cuadrado inverso, por lo que la luz parpadeante que proceda de una luciérnaga hará que las luciérnagas a su alrededor reaccionen a la vista del destello.

Existen dos variantes de algoritmos de optimización de la población inspirados en el comportamiento de las luciérnagas: el algoritmo de luciérnagas (Firefly algorithm) y el algoritmo de optimización con enjambre de luciérnagas (Glowworm Swarm Optimization, GSO). La principal diferencia entre las luciérnagas firefly y glowworm es que estas últimas no tienen alas. En este artículo, analizaremos el primer tipo de algoritmo de optimización.

2. Descripción del algoritmo

El algoritmo de luciérnagas (algoritmo F) fue propuesto en la Universidad de Cambridge (Reino Unido) en 2007 por X-Sh. Yang, e inmediatamente atrajo la atención de los investigadores de optimización. El algoritmo de luciérnagas forma parte de una familia de algoritmos de inteligencia de enjambre que recientemente han mostrado resultados impresionantes en la resolución de problemas de optimización. El algoritmo de luciérnagas, en particular, se utiliza para resolver problemas de optimización continua y discreta.

El algoritmo de luciérnagas tiene tres reglas basadas en las características del destello de las luciérnagas reales. Aquí las tenemos:

1. Todas las luciérnagas se volverán más atrayentes y brillantes.
2. El grado de atracción de una luciérnaga es proporcional a su brillo, que disminuirá a medida que aumente la distancia respecto a otra luciérnaga, debido a que el aire absorbe la luz. Por consiguiente, entre dos luciérnagas parpadeantes, la menos brillante se moverá hacia la más brillante. Si no hay una luciérnaga más brillante o más atrayente que una en particular, se moverá al azar.
3. El brillo o intensidad de la luz de la luciérnaga estará determinado por el valor de la función objetivo del problema.

Inicialmente, al comienzo del algoritmo, todas las luciérnagas se dispersan al azar por todo el espacio de búsqueda. Luego, el algoritmo determina las particiones óptimas considerando dos fases:

1. El cambio en la intensidad de la luz: el brillo de la luciérnaga en su posición actual se refleja en el valor de su estado físico, el movimiento hacia una luciérnaga atrayente.
2. La luciérnaga cambia de posición al observar la intensidad de la luz de las luciérnagas próximas.

Ahora podemos sumergirnos con más detalle en las complejidades de la optimización de luciérnagas. La esencia del algoritmo se muestra claramente en la figura 1.

Figura 1. Luciérnagas en el espacio de búsqueda. Disminución de la visibilidad al incrementarse la distancia.

La idea principal tras el principio de búsqueda es una disminución no lineal de la visibilidad al aumentar la distancia entre las luciérnagas. Sin esta relación no lineal, cada luciérnaga se movería de forma determinista hacia la fuente de luz más brillante. Sin embargo, como vemos en la figura 1, la luciérnaga no elige a su congénere más brillante, ya que su luz es menos perceptible debido a la absorción de la luz por el entorno. En su lugar, elige un homólogo menos luminoso (aunque el más luminoso de su entorno). Esta característica explica la buena capacidad del algoritmo para dividirse en enjambres más pequeños. Esto ocurre de forma natural, debido a la función no lineal de la absorción de la luz por la distancia. En la figura 2, a continuación, podemos ver la función de visibilidad frente a la distancia para el algoritmo con distintos valores del coeficiente de absorción del entorno gamma, que es uno de los parámetros del algoritmo.

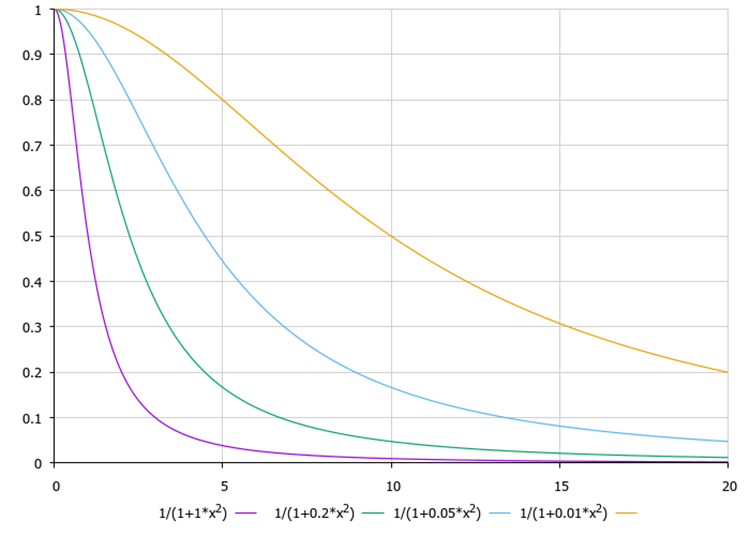
Figura 2. Función de la transparencia del entorno sobre la distancia f(x), donde el coeficiente de transparencia gamma es igual a 1.0, 0.2, 0.05, 0.01, respectivamente.

Cuando gamma tiende a infinito, el entorno se vuelve opaco, y cuando gamma es igual a cero, el entorno es completamente transparente, y cada luciérnaga ve a la otra a cualquier distancia en el espacio de búsqueda. ¿Qué sucede si gamma = 0.0? Respuesta: todas las luciérnagas volarán hacia el congénere más brillante, convergiendo en algún punto no óptimo, y el algoritmo no convergerá, atascándose en uno de los extremos locales. ¿Qué sucederá si el entorno resulta completamente opaco? Esto quiere decir que las luciérnagas no verán a nadie más atrayente que ellas mismas, pero según el concepto propuesto por el autor del algoritmo, al no ver a nadie mejor que ellas mismas, la luciérnaga se moverá aleatoriamente. Es decir, el algoritmo degenerará en una búsqueda aleatoria. En nuestra tabla de clasificación de algoritmos, el algoritmo de búsqueda aleatoria ocupa el último lugar.  

Vamos a profundizar en el análisis adicional del algoritmo; para ello, analizaremos las fórmulas que describen los movimientos de las luciérnagas. La función de visibilidad frente a la distancia subyace en el cálculo del llamado índice de atractivo:

attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

donde:
attractiveness - atractivo
gamma - factor de opacidad del entorno
distance - distancia euclidiana entre luciérnagas
fireflies [k].f - intensidad de la luz de la k-ésima luciérnaga

Por la fórmula, podemos ver que la función de atractivo dependerá directamente de la dimensionalidad del problema, y también dependerá de los límites del valor de la distancia, por lo que el autor del algoritmo recomienda seleccionar el coeficiente de transparencia para el problema de optimización específico. A nuestro juicio, resulta incómodo y requiere mucho tiempo seleccionar parámetros sin saber de antemano cómo se comportará el algoritmo, por lo que será necesario normalizar los valores de distancia en el rango de 0 a 20. Usaremos para ello la función Scale(), que hemos usado repetidamente en otros algoritmos. La transformación de la distancia antes de calcularse el atractivo tendrá el aspecto siguiente:

distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);

donde:

maxDist - distancia euclidiana máxima entre un par de luciérnagas entre todas

En este caso, el atractivo de las luciérnagas no dependerá de la dimensión del problema y no será necesario seleccionar el coeficiente gamma para un problema de optimización específico. La función de atractivo determina qué tipo de elección de pareja hará cada luciérnaga. Esta elección está estrictamente determinada. La influencia del atractivo de las luciérnagas entre sí viene determinado por el coeficiente beta (el segundo parámetro del algoritmo). ¿De qué forma se posibilitan las capacidades de búsqueda del algoritmo si la elección de las luciérnagas ya está determinada de antemano en cada iteración correspondiente? Para ello, introduciremos un componente vectorial aleatorio, así como el tercer parámetro del algoritmo alpha. Las complejas relaciones de comportamiento de las luciérnagas tendría el aspecto que vemos:

fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];

donde:
fireflies [i].c [c] - c-ésima coordenada de la i-ésima luciérnaga
beta - coeficiente de influencia del atractivo de las luciérnagas entre sí
alpha - coeficiente que afecta al componente aleatorio cuando se mueven las luciérnagas, ofreciendo desviaciones respecto al objetivo del movimiento
r - número aleatorio en el rango [-1.0;1.0]
v[c] - componente del vector que caracteriza la distancia entre los puntos extremos del rango de búsqueda por la c-ésima coordenada
Xj - coordenada correspondiente de la luciérnaga en la pareja hacia la que se dará movimiento
Xi - coordenada correspondiente de la luciérnaga para la que se calcula el movimiento

Pasemos a la descripción del código del algoritmo. El código no resulta particularmente complejo, es bastante simple. Echemos un vistazo más detallado.

Se trata de una maravillosa creación de la naturaleza: una luciérnaga, que describiremos con la estructura simple S_Firefly, y en la que solo habrá dos componentes, a saber [] - coordenadas, f - luminosidad de la luciérnaga (función de aptitud). Como para cada luciérnaga solo hay un individuo en la iteración correspondiente hacia el que se moverá formando una pareja, no corremos el riesgo de sobrescribir las coordenadas al calcular el próximo movimiento, ya que para estos efectos introduciremos una estructura especial que analizaremos a continuación.

//——————————————————————————————————————————————————————————————————————————————
struct S_Firefly
{
  double c  []; //coordinates
  double f;     //the value of the fitness function
};
//——————————————————————————————————————————————————————————————————————————————

La estructura S_Attractiveness debe contener el valor de atractivo y el número de la luciérnaga correspondiente como una pareja. Cada luciérnaga no se mueve hacia las coordenadas de la más atrayente, sino hacia las coordenadas a las que ya se ha desplazado su compañero. Esto presenta alguna discrepancia respecto a la versión del algoritmo descrita por el autor, pero así funciona mejor.

//——————————————————————————————————————————————————————————————————————————————
struct S_Attractiveness
{
  double a; //attractiveness
  int    i; //index of the most attractive firefly
};
//——————————————————————————————————————————————————————————————————————————————

Describiremos el algoritmo de luciérnagas con la clase C_AO_FA. Aquí tenemos tres métodos públicos, uno de los cuales es Init() para la inicialización primaria, más dos métodos públicos que deberán llamarse en cada iteración, Flight() y Luminosity(): los métodos auxiliares privados y los miembros para almacenar las constantes de los parámetros.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_FA
{
  //----------------------------------------------------------------------------
  public: S_Firefly fireflies []; //fireflies
  public: double    rangeMax  []; //maximum search range
  public: double    rangeMin  []; //minimum search range
  public: double    rangeStep []; //step search
  public: double    cB        []; //best coordinates
  public: double    fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,  //number of opt. parameters
                     const int    sizeP,    //swarm size
                     const double alphaP,   //alpha, randomness in motion
                     const double betaP,    //beta, effect of attractiveness
                     const double gammaP);  //gamma, transparency of the environment

  public: void Flight ();
  public: void Luminosity ();

  //----------------------------------------------------------------------------
  private: S_Attractiveness att [];
  private: int    swarmSize;
  private: int    params;
  private: double maxDist;
  private: double v [];

  private: double alpha;      //randomness in motion
  private: double beta;       //effect of attractiveness
  private: double gamma;      //transparency of the environment
  private: bool   luminosity;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  protected: double Scale   (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

El método abierto Init() se utiliza para la inicialización y debe llamarse antes del inicio de cada optimización. Sus parámetros son parámetros de superestructura para el algoritmo. El método asignará memoria para los arrays y restablecerá el valor de luminosidad de la luciérnaga global y de cada luciérnaga individual.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Init (const int    paramsP, //number of opt. parameters
                    const int    sizeP,   //swarm size
                    const double alphaP,  //alpha, randomness in motion
                    const double betaP,   //beta, effect of attractiveness
                    const double gammaP)  //gamma, transparency of the environment
{
  fB = -DBL_MAX;

  params    = paramsP;
  swarmSize = sizeP;
  alpha     = alphaP;
  beta      = betaP;
  gamma     = gammaP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);
  ArrayResize (v,         params);
  ArrayResize (att,       swarmSize);

  luminosity = false;

  ArrayResize (fireflies, swarmSize);

  for (int i = 0; i < swarmSize; i++)
  {
    ArrayResize (fireflies [i].c,  params);
    fireflies [i].f = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a analizar el primer método público llamado en cada iteración, Flight(). En este método se concentra toda la lógica esencial del algoritmo, por lo que deberemos estudiarlo con más detalle, por partes. Para determinar si el algoritmo se está ejecutando en la primera iteración o en iteraciones posteriores, la variable de luminosidad servirá como bandera. Si la bandera no está configurada, deberemos distribuir las luciérnagas al azar en el espacio de coordenadas según una distribución uniforme. Junto con esta acción, estableceremos el vector de desplazamiento para cada coordenada e inmediatamente calcularemos la máxima distancia euclidiana posible que pueda existir entre luciérnagas (esto será necesario para normalizar las distancias entre luciérnagas y así evitar la dependencia del coeficiente de transparencia del entorno respecto a la dimensionalidad del problema que analizamos antes). Tras realizar estas operaciones, activaremos la bandera luminosity.

if (!luminosity)
{
  fB = -DBL_MAX;

  //--------------------------------------------------------------------------
  double summCoordinates = 0.0;
  for (int c = 0; c < params; c++)
  {
    v [c] = rangeMax [c] - rangeMin [c];
    summCoordinates += pow (v [c], 2.0);
  }
  maxDist = pow (summCoordinates, 0.5);

  //--------------------------------------------------------------------------
  for (int s = 0; s < swarmSize; s++)
  {
    for (int k = 0; k < params; k++)
    {
      fireflies [s].c  [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      fireflies [s].c  [k] = SeInDiSp (fireflies [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
  }

  luminosity = true;
}

A partir de la segunda iteración y posteriores, después de que las luciérnagas se distribuyeran aleatoriamente en la primera iteración y empezaran a brillar (se calculó la función de aptitud para ellas), resulta posible calcular el grado de atractivo de cada luciérnaga. Para hacer esto, necesitaremos calcular la distancia euclidiana entre todos las posibles parejas de luciérnagas. Así, lograremos este resultado simplemente sumando los cuadrados de las diferencias en coordenadas, y extrayendo la raíz de su suma. La distancia calculada se usará en la fórmula de cálculo del atractivo. Entonces obtenemos para cada luciérnaga la única pareja posible. Inmediatamente, determinaremos la luminosidad máxima entre todas las luciérnagas: esto será necesario para determinar la luciérnaga más brillante para la cual no podremos encontrar una pareja, y que vagará sola en el espacio. Bueno, no pasa nada, quizá tenga más suerte en la próxima iteración.

//measure the distance between all------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  att [i].a = -DBL_MAX;

  for (int k = 0; k < swarmSize; k++)
  {
    if (i == k) continue;

    summCoordinates = 0.0;
    for (int c = 0; c < params; c++) summCoordinates += pow (fireflies [i].c [c] - fireflies [k].c [c], 2.0);

    distance = pow (summCoordinates, 0.5);
    distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);
    attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

    if (attractiveness > att [i].a)
    {
      att [i].a = attractiveness;
      att [i].i = k;
    }

    if (fireflies [i].f > maxF) maxF = fireflies [i].f;
  }
}

Esta parte del código del método Flight() es responsable del vuelo de las luciérnagas. Para esa misma luciérnaga infortunada cuya luminosidad es superior a la de todas las demás, el cálculo se realizará de forma algo diferente. Para ello, sumaremos el vector desplazamiento a su posición actual a través del coeficiente alfa, multiplicado por un número aleatorio [-1.0;1.0]. En teoría, esto actuará en el algoritmo como un estudio adicional sobre la mejor solución, con la expectativa de que esta resulte aún mejor, sin embargo, como veremos más adelante, dicha técnica será inútil. En esta etapa, analizaremos la versión clásica del algoritmo.

Para todas las demás luciérnagas para las que ya se haya encontrado una pareja, el cálculo del movimiento consistirá en desplazarse hasta el punto de la pareja que le corresponda con la adición de un componente aleatorio (hemos hablado de ello antes).

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      fireflies [i].c [c] = fireflies [i].c [c] + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); 
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];
      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Un simple método abierto llamado en cada iteración. Aquí actualizaremos la mejor solución.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Luminosity ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    if (fireflies [i].f > fB)
    {
      fB = fireflies [i].f;
      ArrayCopy (cB, fireflies [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a proceder ahora a discutir las pruebas. Veamos la impresión de los resultados del algoritmo en las funciones de prueba:

2022.12.16 13:39:00.102    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.901742065217812
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    Score: 0.99603
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    20 Skin's; Func runs 10000 result: 3.2208359936020665
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    Score: 0.59468
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    500 Skin's; Func runs 10000 result: 0.98491319842575
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    Score: 0.06082
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.578196881663454
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    Score: 0.89271
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.3101994341994826
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    Score: 0.17546
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.06829102669136165
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    Score: 0.03863
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 8.2
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    Score: 0.68333
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.5900000000000003
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    Score: 0.13250
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.2892
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    Score: 0.02410
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    All score for C_AO_FA: 0.39980648892951776

Los resultados han sido, por decirlo suavemente, poco impresionantes. El algoritmo resulta apenas un poco mejor que algoritmos como PSO, FSS, GWO en pruebas individuales; sin embargo, en el indicador de calificación total, se encuentra en la segunda posición por abajo, siendo mejor solo que el algoritmo de búsqueda aleatoria. Basándonos en lo anteriormente dicho, ha surgido la idea de revisar el cálculo de los indicadores de evaluación en las pruebas, así que en los siguientes artículos pasaremos a usar un esquema de cálculo de calificación más conveniente. En este artículo, añadiremos un histograma con los resultados finales, de esta forma, se podrá mostrar claramente la relación de rendimiento entre algoritmos individuales.

El algoritmo clásico de luciérnagas es fácil de implementar. No obstante, los estudios muestran que converge lentamente y cae fácilmente en la trampa del extremo local para problemas multimodales. Además, carece de coeficientes que dependan paramétricamente de la iteración actual. Por consiguiente, modificar el algoritmo estándar de luciérnagas para mejorar su rendimiento ha sido uno de los objetivos del presente estudio.

La propia idea del algoritmo deslumbra por su originalidad, y sería una pena dejar todo como está y no intentar mejorar sus características. Por ello, hemos tratado de modificar el algoritmo reemplazando el componente aleatorio con un vuelo de Levy. Cabe señalar que no para todos los algoritmos, el vuelo de Levy puede mejorar la capacidad de búsqueda. Después de analizar el algoritmo de búsqueda de cuco, hemos intentado mejorar otros algoritmos usando el método en cuestión, pero esto no ha tenido los resultados esperados. Aparentemente, esto debe resultar consistente de alguna forma con la estrategia de búsqueda interna dentro del algoritmo, complementándolo. En este caso particular, la aplicación del vuelo de Levy ha tenido un efecto sorprendente: las capacidades del algoritmo han aumentado dramáticamente. Hablaremos de ello en el apartado que trata de los resultados de la prueba.

Aquí, de hecho, se encontrará la parte del código donde se ha realizado el cambio. Primero, en la versión clásica, la luciérnaga con la mejor luminosidad se mueve en una dirección aleatoria desde su posición actual; luego nuestra mejor luciérnaga se moverá desde la mejor posición global, intentando mejorar no su posición actual, sino la solución en su conjunto. A las coordenadas de la mejor solución le sumamos un número aleatorio de la distribución del vuelo de Levy (distribución con colas pesadas) con el mismo coeficiente alpha, teniendo en cuenta el vector desplazamiento. Esto realmente ha hecho posible mejorar las coordenadas de la solución global, precisando las proximidades.

Como podemos ver, el comportamiento del resto de las luciérnagas ahora obedece a las mismas reglas clásicas, pero ajustadas por el componente aleatorio del vuelo de Levy. Esas son todas las modificaciones que le hemos hecho al algoritmo.

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      fireflies [i].c [c] = cB [c] + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];

      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Gráfico de la función de vuelo de Levy en la figura 3. ¿Cómo puede el exponente en la fórmula de una función influir en el comportamiento del algoritmo? Según nuestra investigación, a medida que aumenta el grado, la cantidad de saltos largos (colas pesadas) disminuye en relación con los cortos, al tiempo que mejora la capacidad del algoritmo para precisar las coordenadas en las proximidades de la mejor solución. No obstante, debido al hecho de que hay pocos saltos largos, aumentará la probabilidad de quedarse atascado en los extremos locales. Este efecto resultará más acusado al estudiar funciones discretas, mientras que no será tan pronunciado en las funciones suaves. Por el contrario, con una disminución en el grado, el número de saltos largos aumenta y las capacidades de búsqueda del algoritmo mejoran, pero la precisión de la convergencia empeora, por lo que necesitaremos un término medio entre la precisión y la búsqueda; esta, además, podrá resultar diferente dependiendo del problema de optimización.

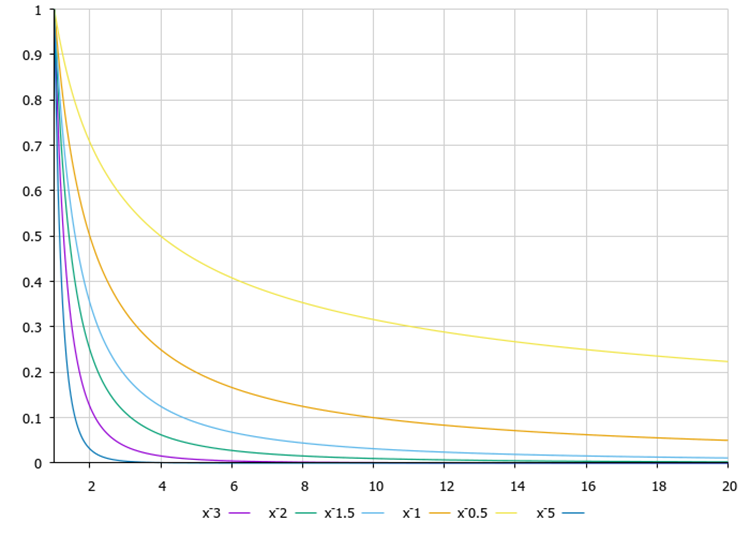
Figura 3. Función de vuelo de Levy, grados 0,5...3,0. 

Bien, vamos a pasar a los resultados de la versión modificada del algoritmo en el banco de pruebas. A continuación, le mostramos una impresión donde podrá ver cuánto ha mejorado el rendimiento de la versión original en comparación con la versión clásica.

2022.12.16 13:07:15.925    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.854437214435259
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    Score: 0.98473
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    20 Skin's; Func runs 10000 result: 4.588539001298423
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    Score: 0.92124
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.981278990090829
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    Score: 0.29872
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.7665409595127233
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    Score: 0.99924
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.6261364994589462
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    Score: 0.35417
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.14269062630878
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    Score: 0.08071
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 10.0
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    Score: 0.83333
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.7899999999999998
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    Score: 0.14917
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.5076
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    Score: 0.04230
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    All score for C_AO_FAm: 0.5181804234713119

Como puede ver, el algoritmo modificado no solo ha mostrado mejores resultados, sino que también ha logrado auparse a la primera plaza en la tabla de calificación. Echaremos un vistazo más de cerca a los resultados en la siguiente sección. A continuación, le mostramos una animación de la versión modificada del algoritmo en el banco de pruebas.

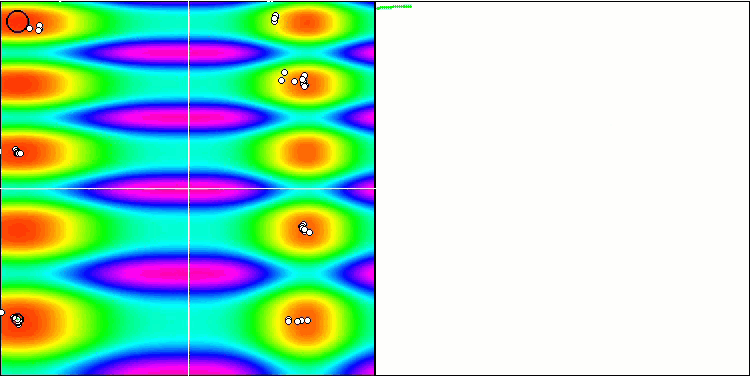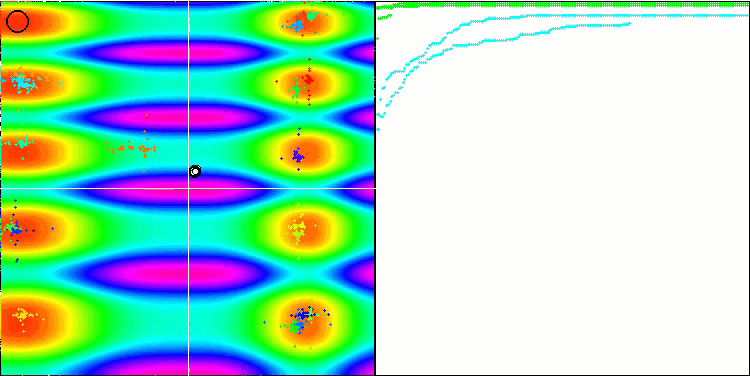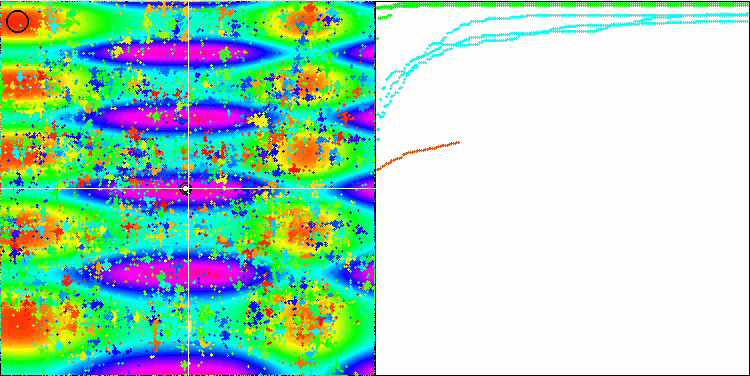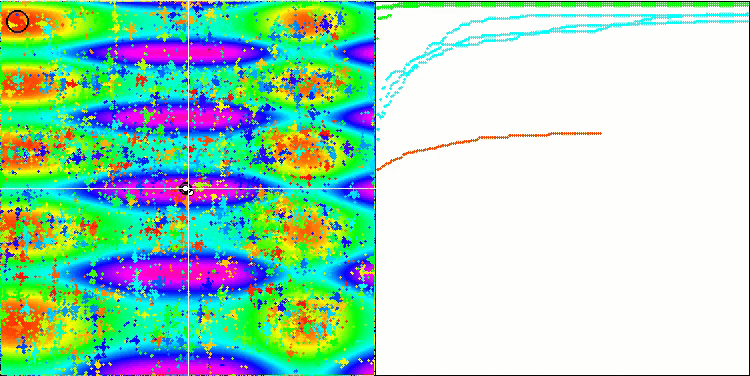
  FAm en la función de prueba Skin.

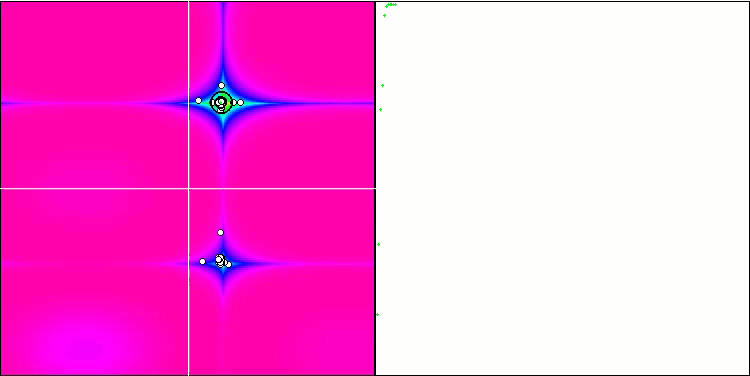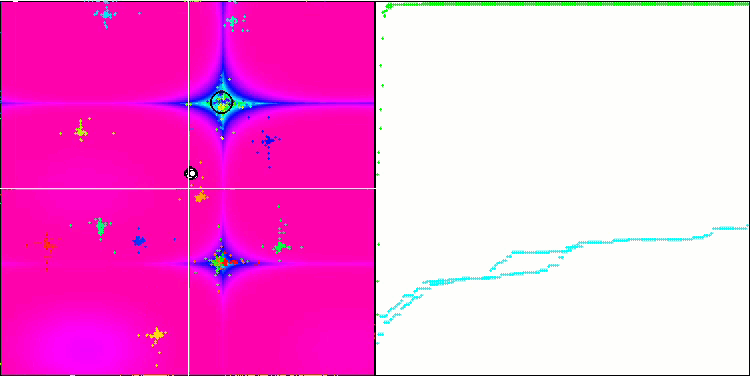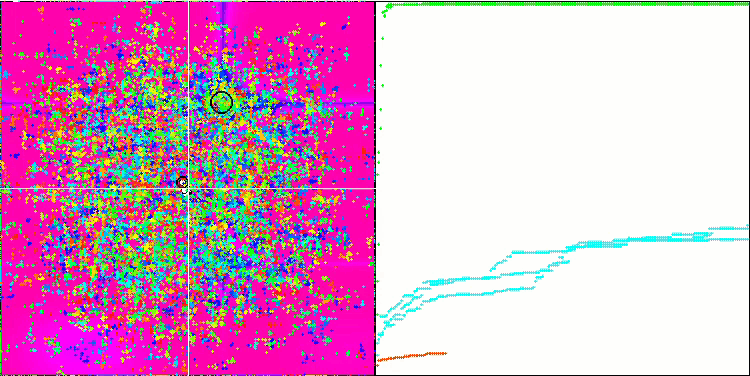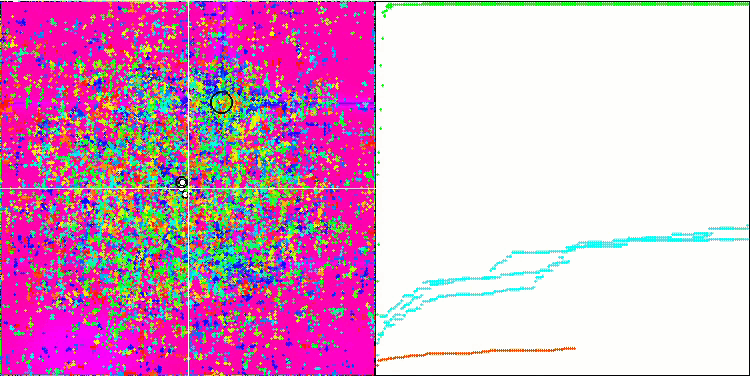
  FAm en la función de prueba Forest.

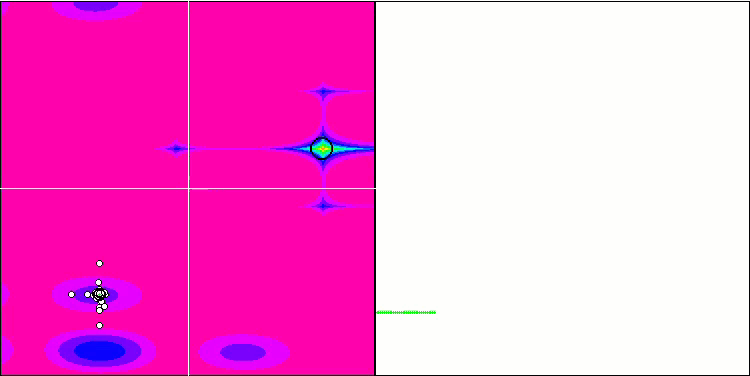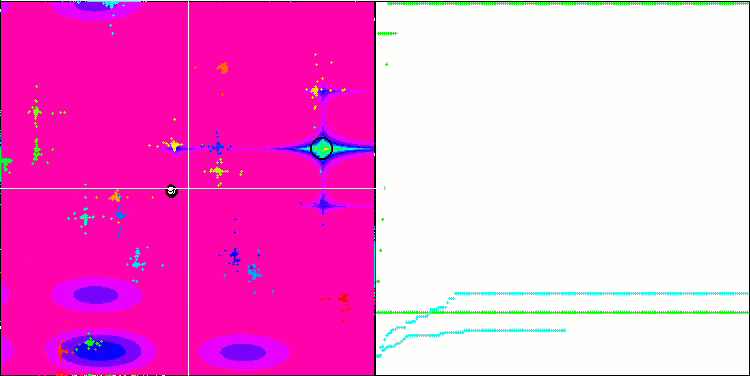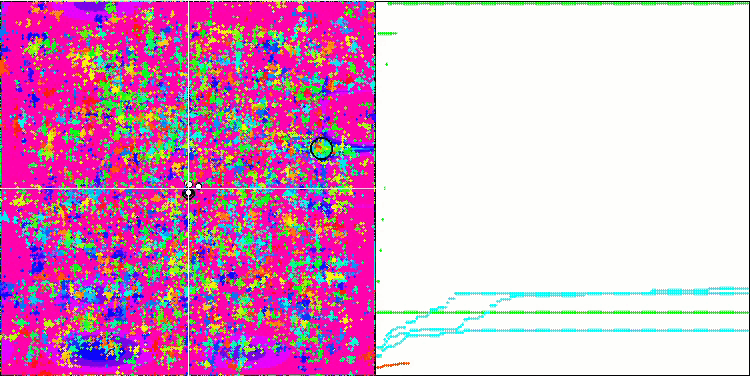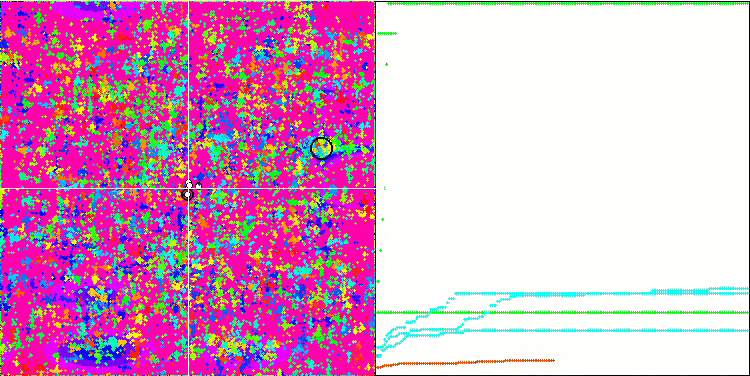
  FAm en la función de prueba Megacity.

3. Resultados de las pruebas

El algoritmo de luciérnagas modificado (FAm) ha rendido excelentemente en todas las pruebas. En general, los resultados dependen de la configuración del algoritmo, con algunas configuraciones, se ha logrado una convergencia del 100 % en las tres funciones con dos variables. La alta escalabilidad del algoritmo ha hecho posible el liderazgo en las pruebas con 40 y 1000 parámetros. Los parámetros beta y gamma tienen una fuerte influencia, lo cual permite obtener tanto una alta convergencia como una alta resistencia a atascarse en los extremos locales. Los resultados varían ampliamente, lo que en general puede atribuirse a las desventajas del algoritmo. En igualdad de condiciones, este algoritmo es el más potente de los considerados anteriormente. Podemos recomendar su uso en una gama muy amplia de tareas, incluidas las de aprendizaje automático e inteligencia artificial, en particular a la hora de entrenar redes neuronales.

A continuación, le mostramos la tabla de clasificación final, en la que el algoritmo de luciérnagas modificado es el líder. El algoritmo clásico, a pesar de su originalidad, lamentablemente no ha logrado buenos resultados, y la selección de parámetros de ajuste no ha tenido éxito.

AO	Description	Skin			Skin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		2 params (1 F)	40 params (20 F)	1000 params (500 F)		2 params (1 F)	40 params (20 F)	1000 params (500 F)		2 params (1 F)	40 params (20 F)	1000 params (500 F)
FAm	firefly algorithm M	0,98473	0,92124	0,29872	0,73490	0,99924	0,35417	0,08071	0,47804	0,83333	0,14917	0,04230	0,34160	0,51817889
COAm	cuckoo optimization algorithm M	1,00000	0,85911	0,14316	0,66742	0,99283	0,28787	0,04551	0,44207	1,00000	0,24917	0,03537	0,42818	0,51255778
ACOm	ant colony optimization M	0,98229	0,79108	0,12602	0,63313	1,00000	0,62077	0,11521	0,57866	0,38333	0,44000	0,02377	0,28237	0,49805222
ABCm	artificial bee colony M	1,00000	0,63922	0,08076	0,57333	0,99908	0,20112	0,03785	0,41268	1,00000	0,16333	0,02823	0,39719	0,46106556
ABC	artificial bee colony	0,99339	0,73381	0,11118	0,61279	0,99934	0,21437	0,04215	0,41862	0,85000	0,16833	0,03130	0,34988	0,46043000
GWO	grey wolf optimizer	0.99900	0,48033	0,18924	0,55619	0,83844	0,08755	0,02555	0,31718	1,00000	0,10000	0,02187	0,37396	0,41577556
FSS	búsqueda de bancos de peces	0,99391	0,5692	0,11341	0,55884	0,85172	0,12143	0,03223	0,33513	0,91667	0,08583	0,02583	0,34278	0,41224778
PSO	particle swarm optimisation	0,99627	0,38080	0,05089	0,47599	0,93772	0.14540	0,04856	0,37723	1,00000	0,09333	0,02233	0,37189	0,40836667
FA	firefly algorithm	0,99603	0,59468	0,06082	0,55051	0,89271	0,17546	0,03863	0,36893	0,68333	0,13250	0,02410	0,27998	0,39980649
RND	random	0,99932	0,44276	0,06827	0,50345	0,83126	0,11524	0,03048	0.32566	0,83333	0,09000	0,02403	0,31579	0,38163222

A partir de este artículo, publicaremos un histograma en el que el mejor algoritmo en el momento de la prueba tendrá 100 puntos condicionales, mientras que el peor tendrá 1 punto. A nuestro juicio, este método será el más conveniente para la percepción visual, pues veremos claramente la escala de resultados finales de los algoritmos en la tabla de calificación. Ahora podremos ver cuánto se retrasa el algoritmo aleatorio con respecto al líder.

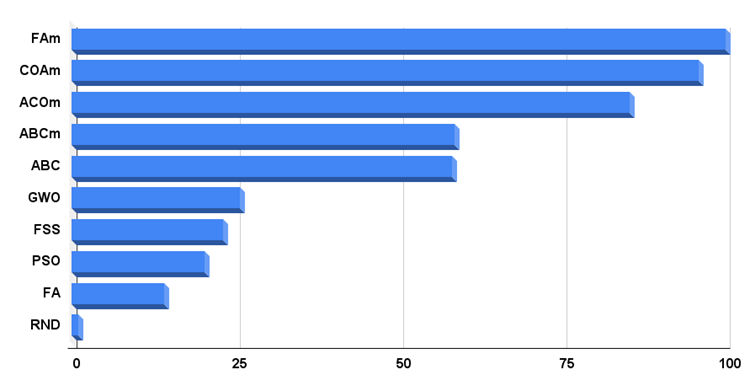
Figura 4. Histograma con los resultados finales de los algoritmos de prueba.

Recuerde que los algoritmos metaheurísticos son métodos aproximados para resolver problemas de optimización que usan en su mecanismo de búsqueda la propiedad de la aleatoriedad con una conjetura justificada y tratan de mejorar la calidad de las soluciones disponibles a través de iteraciones de un conjunto de soluciones válidas generadas aleatoriamente mediante el examen y el uso del espacio de soluciones. Aunque no se puede garantizar que estos algoritmos resulten óptimos, se ponen a prueba para ofrecer una solución razonable y aceptable. Además, tienen la ventaja de que el comportamiento del problema no les afecta mucho, y esto es lo que los hace útiles en muchas tareas. La existencia de muchos algoritmos disponibles hace posible seleccionar el apropiado para resolver un problema concreto, dependiendo de su comportamiento.

Desde la aparición de los algoritmos evolutivos, se ha investigado mucho sobre los algoritmos heurísticos. La implementación de nuevos algoritmos ha sido una de las principales áreas de investigación. Actualmente, existen más de 40 algoritmos metaheurísticos, la mayoría de los cuales se crean simulando un escenario procedente de la naturaleza.

Los ventajas y desventajas se refieren a la versión modificada del algoritmo de luciérnagas (FAm).

Ventajas:

• Implementación sencilla. Fácil de modificar.
• Alta escalabilidad.
• Alta convergencia (variará según la configuración del algoritmo).
• Posee la propiedad de clusterizar el área del espacio de búsqueda en grupos separados alrededor de los extremos locales.

Desventajas:

• Fuerte influencia de la configuración en los resultados de optimización.
• Debe tenerse en cuenta que con algunas configuraciones, el algoritmo resulta propenso a atascarse en los extremos locales.

Para cada artículo, adjuntamos un archivo que contiene las versiones actualizadas actuales de los códigos de algoritmo para todos los artículos anteriores. Cada nuevo artículo supone la experiencia personal acumulada del autor: tanto las conclusiones como los juicios se basan en los experimentos realizados en un banco de pruebas especial desarrollado para este propósito.