Algorithmen zur Populationsoptimierung

MetaTrader 5 — Beispiele | 24 Oktober 2022, 09:29

181

„Im Universum findet überhaupt nichts statt,
in denen keine Maximal- oder Minimalregel vorkommt“
Leonhard Euler, 18. Jahrhundert

Inhalt:

1. Historische Perspektive

Optimierungsalgorithmen sind Algorithmen, die es ermöglichen, Extrempunkte in einem Funktionsbereich zu finden, an denen die Funktion ihren minimalen oder maximalen Wert erreicht.

Das wussten schon die griechischen Gelehrten des Altertums:

— Von allen Formen mit einem bestimmten Umfang hat der Kreis die größte Fläche.

— Von allen Polygonen mit einer bestimmten Anzahl von Seiten und einem bestimmten Umfang hat ein regelmäßiges Polygon die größte Fläche.

— Von allen dreidimensionalen Figuren, die eine bestimmte Fläche haben, hat die Kugel das größte Volumen.

Etwa zur gleichen Zeit wurde auch das erste Problem mit Variationslösungen vorgeschlagen. Der Legende nach geschah dies um 825 v. Chr. Dido, die Schwester des Königs der phönizischen Stadt Tyrus, ist an die Südküste des Mittelmeers gezogen und bittet einen lokalen Stamm um ein Stück Land, das mit einem Stierfell umspannt werden kann. Die Einheimischen gaben ihr daraufhin ein Fell. Das findige Mädchen schnitt es in schmale Streifen und knotete sie zu einem Seil zusammen. Mit diesem Seil eroberte sie das Gebiet vor der Küste und gründete dort die Stadt Karthago.

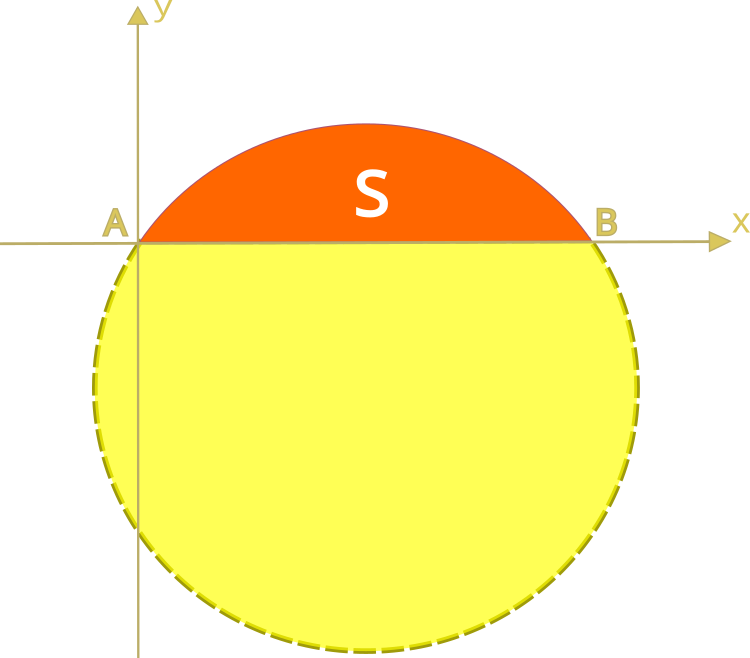
Ihr Problem besteht darin, die effizienteste Kurve einer festgelegten Länge zu finden, die die größte Fläche umspannt. Die maximale Fläche in diesem Problem wird durch die Fläche dargestellt, die von einem Halbkreis umschrieben wird.

dido1

Überspringen wir einen großen Teil der Geschichte, einschließlich der antiken Kultur des Mittelmeers, der Unterdrückung durch die Inquisition und der Quacksalberei des Mittelalters, bis hin zur Renaissance mit ihrem freien Lauf der Gedanken und neuen Theorien. Im Juni 1696 veröffentlicht Johann Bernoulli den folgenden Text für die Leser der Acta Eruditorum: „Ich, Johann Bernoulli, wende mich an die brillantesten Mathematiker der Welt. Nichts ist für intelligente Menschen attraktiver als ein ehrliches, herausforderndes Problem, dessen mögliche Lösung Ruhm einbringt und ein bleibendes Denkmal darstellt. Dem Beispiel Pascals, Fermats usw. folgend, hoffe ich, die Dankbarkeit der gesamten wissenschaftlichen Gemeinschaft zu gewinnen, indem ich den besten Mathematikern unserer Zeit ein Problem stelle, das ihre Methoden und die Stärke ihres Intellekts auf die Probe stellen wird. Wenn mir jemand die Lösung des vorgeschlagenen Problems mitteilt, werde ich ihn öffentlich für würdig erklären“.

Johann Bernullis Problem der Brachistochrone:

„Gegeben seien zwei Punkte A und B in einer vertikalen Ebene. Wie lautet die Kurve, die von A nach B gezeichnet auf der eine Masse nur durch die Einwirkung der Schwerkraft den Punkt B in kürzester Zeit erreicht?“ Bemerkenswerterweise versuchte Galilei bereits 1638, also lange vor der Veröffentlichung von Bernoulli, ein ähnliches Problem zu lösen. Die Antwort: Der schnellste Weg von einem Punkt zum anderen ist nicht der kürzeste Weg, wie es auf den ersten Blick scheint, keine gerade Linie, sondern eine Kurve — eine Zykloide, die die Krümmung der Kurve an jedem Punkt bestimmt.

Brachistochrone9

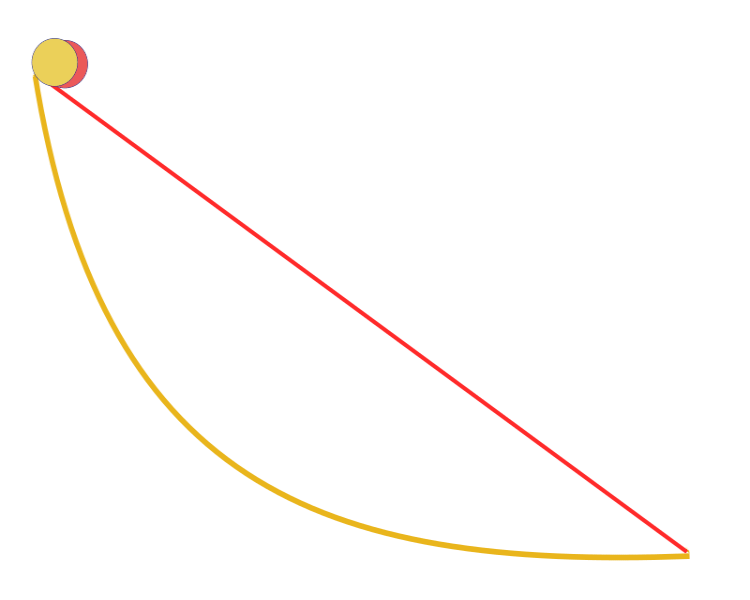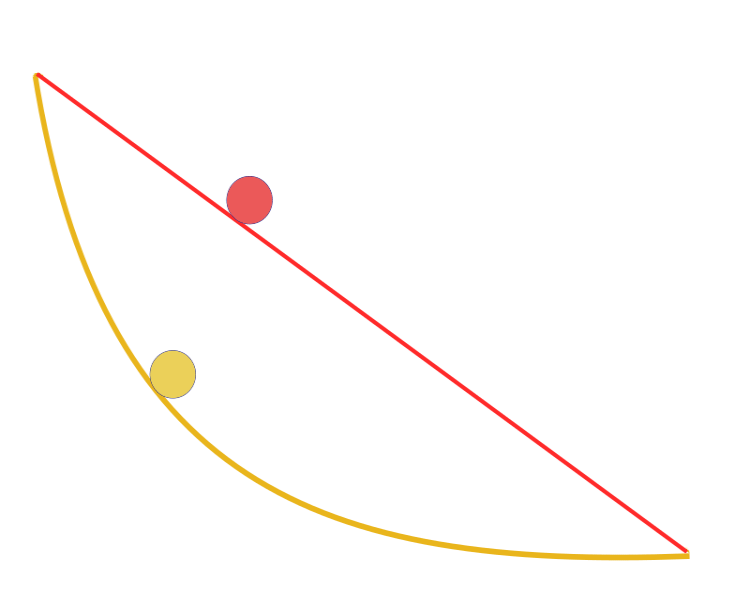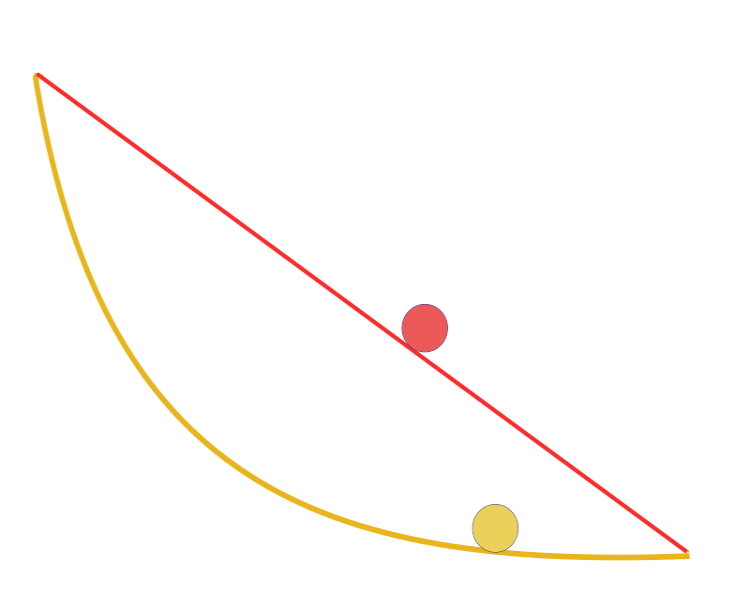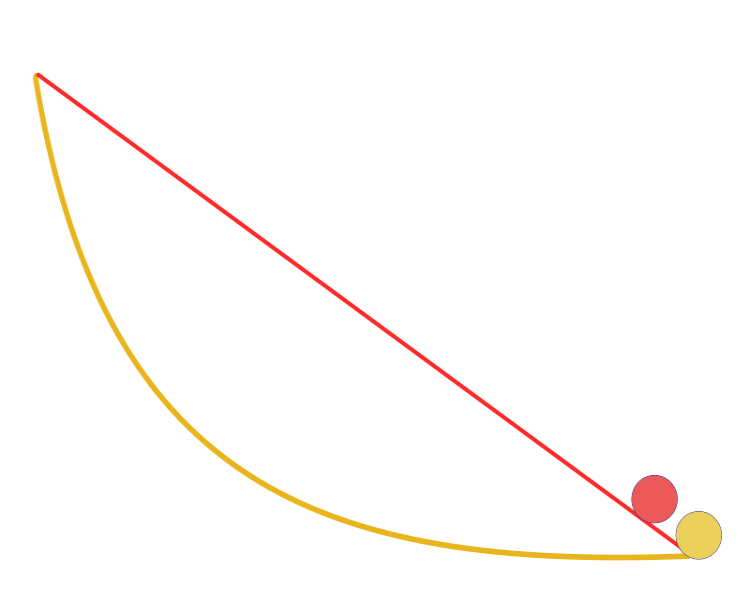
Eine Brachistochrone

Alle anderen Lösungen, auch die von Newton (die damals noch nicht bekannt waren), beruhen auf der Ermittlung der Steigung an jedem Punkt. Die Methode hinter der von Isaac Newton vorgeschlagenen Lösung bildet die Grundlage der Variationsrechnung. Die Methoden der Variationsrechnung werden in der Regel bei der Lösung von Problemen angewendet, bei denen die Optimalitätskriterien in Form von Funktionalen vorliegen und deren Lösungen unbekannte Funktionen sind. Solche Probleme treten normalerweise bei der statischen Optimierung von Prozessen mit verteilten Parametern oder bei dynamischen Optimierungsproblemen auf.

Extremwertbedingungen erster Ordnung in der Variationsrechnung wurden von Leonard Euler und Joseph Lagrange aufgestellt (die Euler-Lagrange-Gleichungen). Diese Gleichungen werden häufig bei Optimierungsproblemen verwendet und zusammen mit dem Prinzip der stationären Bewegung bei der Berechnung von Flugbahnen in der Mechanik eingesetzt. Bald wurde jedoch klar, dass die Lösungen dieser Gleichungen nicht immer ein echtes Extremum ergeben, was bedeutet, dass hinreichende Bedingungen erforderlich sind, die dessen Auffinden garantieren. Die Arbeit wurde fortgesetzt und zweiter Ordnung Extremum Bedingungen abgeleitet wurden von Legendre und Jacobi, und dann durch die Schüler des letzteren, Hesse. Die Frage nach der Existenz einer Lösung in der Variationsrechnung wurde erstmals von Weierstraß in der zweiten Hälfte des 19. Jahrhunderts gestellt.

In der zweiten Hälfte des 18. Jahrhunderts bildete die Suche nach optimalen Lösungen für die Probleme die mathematischen Grundlagen und Prinzipien der Optimierung. Leider fanden Optimierungsmethoden bis in die zweite Hälfte des 20. Jahrhunderts in vielen Bereichen von Wissenschaft und Technik kaum Anwendung, da der praktische Einsatz mathematischer Methoden enorme Rechenressourcen erforderte. Das Aufkommen neuer Rechentechnologien in der modernen Welt hat es endlich möglich gemacht, komplexe Optimierungsmethoden zu implementieren, was zu einer großen Vielfalt an verfügbaren Algorithmen geführt hat.

In den 1980er Jahren begann die intensive Entwicklung der Klasse der stochastischen Optimierungsalgorithmen, die das Ergebnis einer der Natur entlehnten Modellierung sind.

2. OA-Klassifizierung

Klasse

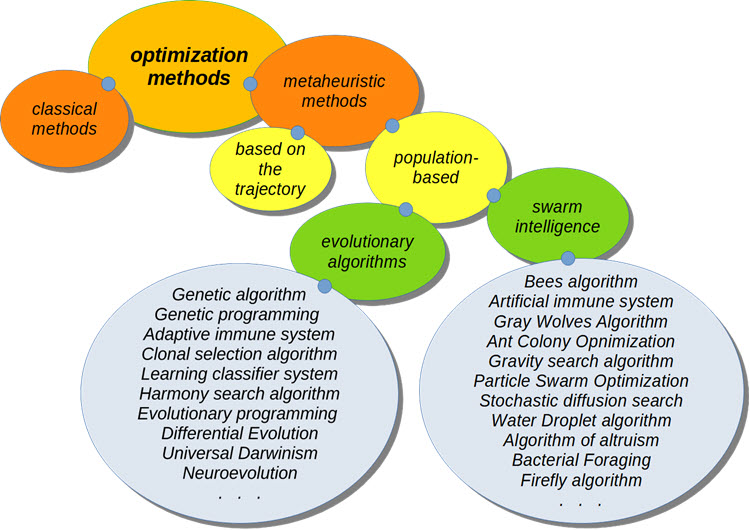
Klassifizierung AO

Das Spannendste bei der Optimierung von Handelssystemen sind metaheuristische Optimierungsalgorithmen. Sie erfordern keine Kenntnis der Formel der zu optimierenden Funktion. Ihre Konvergenz zum globalen Optimum ist nicht bewiesen, aber es wurde experimentell festgestellt, dass sie in den meisten Fällen eine recht gute Lösung liefern, die für eine Reihe von Problemen ausreichend ist.

Viele OAs entstanden als Modelle, die der Natur entlehnt wurden. Solche Modelle werden auch als Verhaltens-, Schwarm- oder Populationsmodelle bezeichnet, wie z. B. das Verhalten von Vögeln in einem Schwarm (der Partikelschwarm-Algorithmus) oder die Prinzipien des Verhaltens von Ameisenkolonien (Ameisen-Algorithmus).

Populationsalgorithmen beinhalten die gleichzeitige Bearbeitung mehrerer Optionen zur Lösung des Optimierungsproblems und stellen eine Alternative zu klassischen Algorithmen dar, die auf Bewegungstrajektorien basieren und in deren Suchbereich sich nur ein Kandidat zur Lösung des Problems entwickelt.

3. Konvergenz und Konvergenzrate, Konvergenzstabilität, Skalierbarkeit des Optimierungsalgorithmus

Effizienz, Geschwindigkeit, Konvergenz sowie die Auswirkungen der Problembedingungen und Algorithmusparameter erfordern eine sorgfältige Analyse für jede algorithmische Implementierung und für jede Klasse von Optimierungsproblemen.

3.1) Konvergenz und Konvergenzrate

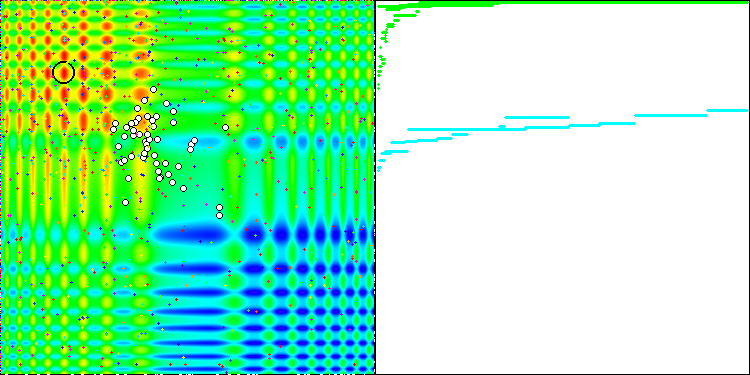
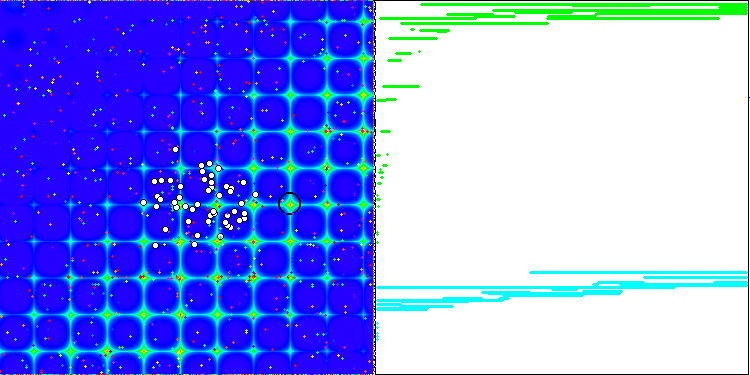
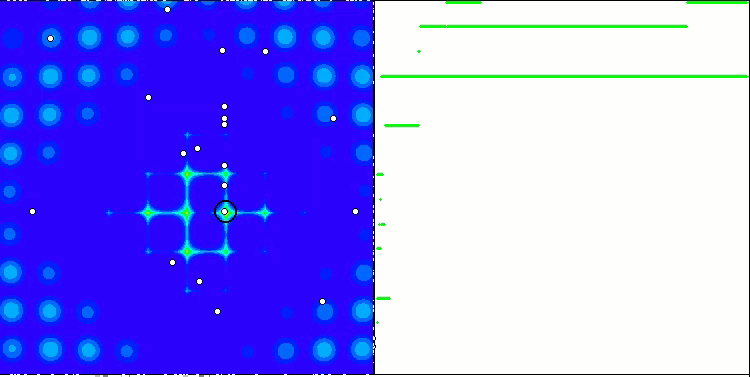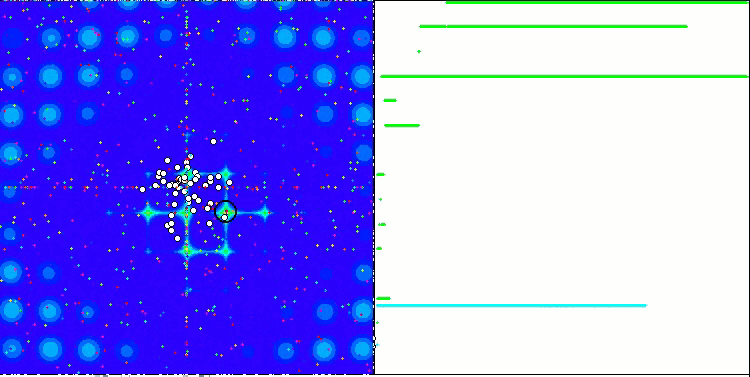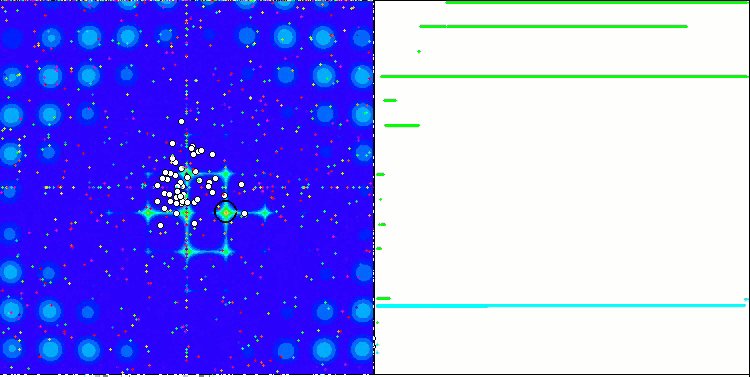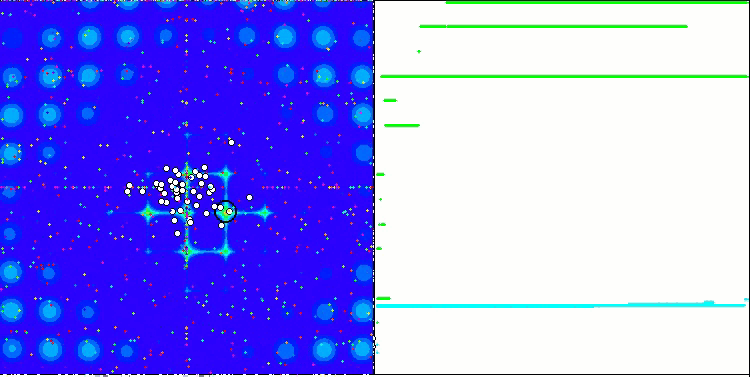
Die Eigenschaft eines iterativen Algorithmus, das Optimum der Zielfunktion in einer endlichen Anzahl von Schritten zu erreichen oder ihm ausreichend nahe zu kommen. Auf der rechten Seite der obigen Screenshots sehen wir ein iterativ erstelltes Diagramm der Ergebnisse, die sich aus der berechneten Testfunktion ergeben. Anhand dieser beiden Bilder können wir feststellen, dass die Konvergenz von der Komplexität der Funktionsfläche beeinflusst wird. Je komplexer es ist, desto schwieriger ist es, das globale Extremum zu finden.

Die Konvergenzrate der Algorithmen ist einer der wichtigsten Indikatoren für die Qualität eines Optimierungsalgorithmus und eines der Hauptmerkmale von Optimierungsverfahren. Wenn wir hören, dass ein Algorithmus schneller ist als ein anderer, ist damit in den meisten Fällen die Konvergenzrate gemeint. Je näher das Ergebnis am globalen Extremwert liegt und je schneller es erreicht wird (d. h. je früher die Iterationen des Algorithmus), desto höher ist dieser Parameter. Beachten Sie, dass die Konvergenzrate der Methoden in der Regel die quadratische Rate nicht überschreitet. In seltenen Fällen kann die Methode eine kubische Konvergenzrate aufweisen.

3.2) Konvergenzstabilität

Die Anzahl der Iterationen, die erforderlich sind, um ein Ergebnis zu erzielen, hängt nicht nur von der Suchfähigkeit des Algorithmus selbst, sondern auch von der untersuchten Funktion ab. Wenn die Funktion durch eine hohe Komplexität der Oberfläche gekennzeichnet ist (Vorhandensein von scharfen Krümmungen, Diskretion, Diskontinuitäten), kann sich der Algorithmus als instabil erweisen und überhaupt keine akzeptable Genauigkeit liefern. Darüber hinaus kann die Konvergenzstabilität als die Wiederholbarkeit der Optimierungsergebnisse bei mehreren aufeinanderfolgenden Versuchen verstanden werden. Weichen die Ergebnisse stark voneinander ab, dann ist die Stabilität des Algorithmus gering.

3.3) Skalierbarkeit des Optimierungsalgorithmus

Konvergenz7 Konvergenz6

Die Skalierbarkeit von Optimierungsalgorithmen ist die Fähigkeit, die Konvergenz mit zunehmender Dimension des Problems aufrechtzuerhalten. Mit anderen Worten: Mit zunehmender Anzahl der Variablen der optimierten Funktion sollte die Konvergenz auf einem für praktische Zwecke akzeptablen Niveau bleiben. Populationsalgorithmen der Suchoptimierung haben im Vergleich zu klassischen Algorithmen unbestreitbare Vorteile, insbesondere bei der Lösung hochdimensionaler und schlecht formalisierter Probleme. Unter diesen Bedingungen können Populationsalgorithmen eine hohe Wahrscheinlichkeit bieten, das globale Extremum der zu optimierenden Funktion zu lokalisieren.

Im Falle einer glatten und unimodalen optimierten Funktion sind Populationsalgorithmen im Allgemeinen weniger effizient als jede klassische Gradientenmethode. Zu den Nachteilen der Populationsalgorithmen gehört auch eine starke Abhängigkeit ihrer Effizienz von den Freiheitsgraden (der Anzahl der Abstimmungsparameter), die bei den meisten Algorithmen recht zahlreich sind.

4. Testfunktionen, Konstruktion eines komplexen OA-Bewertungskriteriums

Es gibt keine allgemein anerkannte Methodik zum Testen und Vergleichen von Optimierungsalgorithmen. Es gibt jedoch viele Testfunktionen, die von Forschern in verschiedenen Jahren vorgeschlagen wurden. Wir werden die Funktionen verwenden, die ich vor der Veröffentlichung des ersten Artikels erstellt habe. Diese Funktionen befinden sich im Terminalordner \MQL5\Experts\Examples\Math 3D\Functions.mqh und \MQL5\Experts\Examples\Math 3D Morpher\Functions.mqh. Diese Funktionen erfüllen alle Komplexitätskriterien für OA-Tests. Zusätzlich wurden die Funktionen Forest und Megacity entwickelt, um eine umfassendere Untersuchung der OA-Suchmöglichkeiten zu ermöglichen.

Testfunktion Skin:

Die Funktion ist in ihrem gesamten Bereich glatt und hat viele lokale Maximal-/Minimalwerte, die sich nur unwesentlich unterscheiden (Konvergenzfallen), was dazu führt, dass Algorithmen, die das globale Extremum nicht erreichen, stecken bleiben.

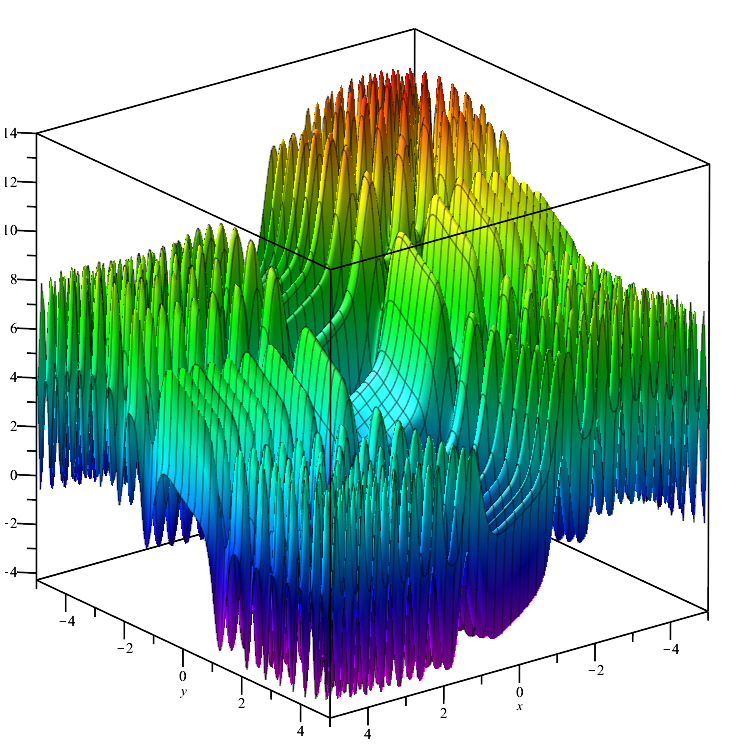
Skin

Testfunktion Forest:

Die Funktion stellt mehrere Maxima dar, die an ihren Punkten kein Differential aufweisen. Daher kann es sich für Optimierungsalgorithmen, deren Robustheit entscheidend von der Glattheit der untersuchten Funktion abhängt, als schwierig erweisen.

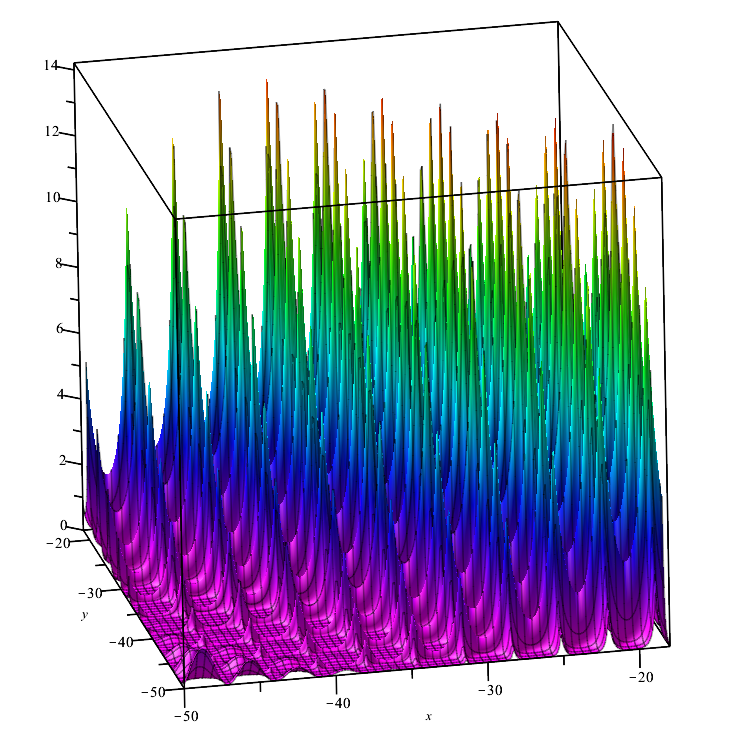
Forest

Testfunktion Megacity:

Eine diskrete Funktion, die „Bereiche“ bildet (in denen eine Änderung der Variablen nicht zu einer signifikanten Änderung des Funktionswertes führt). Daher stellt sie eine Schwierigkeit für Algorithmen dar, die einen Gradienten benötigen.

Chinatown

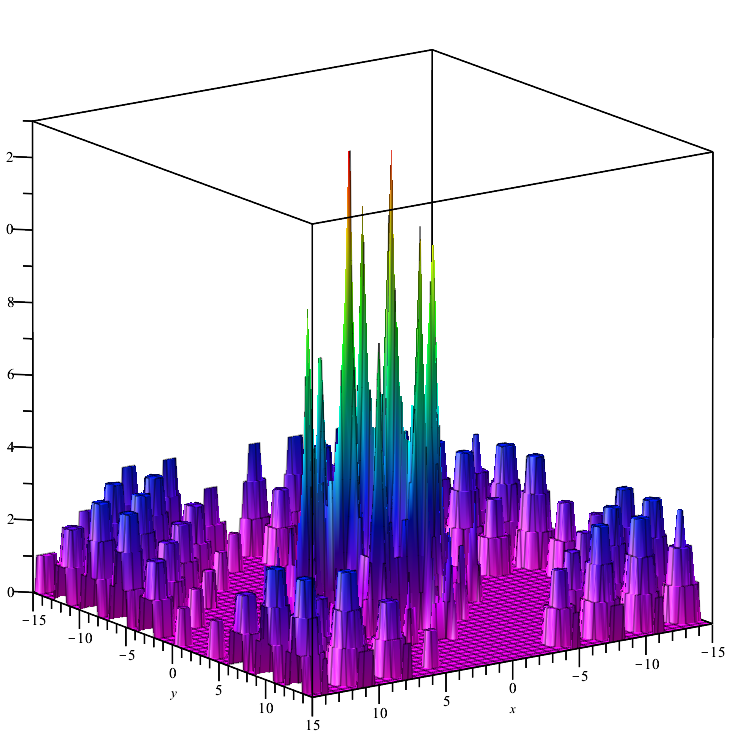
Megacity

5. Prüfstand

Um einen umfassenden Vergleich von Optimierungsalgorithmen zu ermöglichen, wurde versucht, ein allgemeines Bewertungskriterium zu erstellen. Die Komplexität dieser Idee liegt in der Tatsache, dass es nicht klar ist, wie man Algorithmen vergleichen kann, da jeder von ihnen auf seine eigene Weise für die entsprechende Problemklasse gut ist. Ein Algorithmus konvergiert beispielsweise schnell, skaliert aber nicht gut, während ein anderer gut skaliert, aber instabil ist.

Konvergenz: Um die Konvergenz zu untersuchen, verwenden wir die drei oben vorgestellten Funktionen. Ihr Maximum und Minimum werden in einen Bereich von 0,0 (schlechtestes Ergebnis) bis 1,0 (bestes Ergebnis) umgewandelt, was es uns ermöglicht, die Fähigkeit der Algorithmen zu bewerten, die Konvergenz bei verschiedenen Arten von Problemen zu gewährleisten.
Konvergenzrate: Die besten Ergebnisse des Algorithmus werden bei der 1000sten und 10.000sten Ausführung der getesteten Funktion gemessen. So können wir sehen, wie schnell die OA konvergiert. Je schneller die Konvergenz, desto stärker ist der Konvergenzgraph zum Maximum hin gekrümmt.
Stabilität: Wir führen für jede der Funktionen fünf Optimierungsläufe durch und berechnen den Durchschnittswert im Bereich von 0,0 bis 1,0. Dies ist notwendig, da die Ergebnisse einiger Algorithmen von Lauf zu Lauf stark variieren können. Je höher die Konvergenz in jedem der fünf Tests ist, desto höher ist die Stabilität.
Skalierbarkeit: Einige OAs können nur praktische Ergebnisse zu Funktionen mit einer kleinen Anzahl von Variablen zeigen, z. B. nicht mehr als zwei, und einige sind nicht einmal in der Lage, mit mehr als einer Variablen zu arbeiten. Darüber hinaus gibt es Algorithmen, die mit Funktionen mit tausend Variablen arbeiten können. Solche Optimierungsalgorithmen können als OA für neuronale Netze verwendet werden.

Um die Verwendung von Testfunktionen zu erleichtern, schreiben wir eine übergeordnete Klasse und einen Enumerator, mit dem wir in Zukunft ein Objekt der untergeordneten Klasse der entsprechenden Testfunktion auswählen können:

//——————————————————————————————————————————————————————————————————————————————
class C_Function
{
  public: //====================================================================
  double CalcFunc (double &args [], //function arguments
                   int     amount)  //amount of runs functions
  {
    double x, y;
    double sum = 0.0;
    for (int i = 0; i < amount; i++)
    {
      x = args [i * 2];
      y = args [i * 2 + 1];

      sum += Core (x, y);
    }

    sum /= amount;

    return sum;
  }
  double GetMinArg () { return minArg;}
  double GetMaxArg () { return maxArg;}
  double GetMinFun () { return minFun;}
  double GetMaxFun () { return maxFun;}
  string GetNamFun () { return fuName;}

  protected: //==================================================================
  void SetMinArg (double min) { minArg = min;}
  void SetMaxArg (double max) { maxArg = max;}
  void SetMinFun (double min) { minFun = min;}
  void SetMaxFun (double max) { maxFun = max;}
  void SetNamFun (string nam) { fuName = nam;}

  private: //====================================================================
  virtual double Core (double x, double y) { return 0.0;}
  
  double minArg;
  double maxArg;
  double minFun;
  double maxFun;
  string fuName;
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
enum EFunc
{
  Skin,
  Forest,
  Megacity,
  
};
C_Function *SelectFunction (EFunc f)
{
  C_Function *func;
  switch (f)
  {
    case  Skin:
      func = new C_Skin (); return (GetPointer (func));
    case  Forest:
      func = new C_Forest (); return (GetPointer (func));
    case  Megacity:
      func = new C_Megacity (); return (GetPointer (func));
    
    default:
      func = new C_Skin (); return (GetPointer (func));
  }
}
//——————————————————————————————————————————————————————————————————————————————

Dann sehen die abgeleiteten Klassen wie folgt aus:

//——————————————————————————————————————————————————————————————————————————————
class C_Skin : public C_Function
{
  public: //===================================================================
  C_Skin ()
  {
    SetNamFun ("Skin");
    SetMinArg (-5.0);
    SetMaxArg (5.0);
    SetMinFun (-4.3182);  //[x=3.07021;y=3.315935] 1 point
    SetMaxFun (14.0606);  //[x=-3.315699;y=-3.072485] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a1=2*x*x;
    double a2=2*y*y;
    double b1=MathCos(a1)-1.1;
    b1=b1*b1;
    double c1=MathSin(0.5*x)-1.2;
    c1=c1*c1;
    double d1=MathCos(a2)-1.1;
    d1=d1*d1;
    double e1=MathSin(0.5*y)-1.2;
    e1=e1*e1;

   double res=b1+c1-d1+e1;
   return(res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Forest : public C_Function
{
  public: //===================================================================
  C_Forest ()
  {
    SetNamFun ("Forest");
    SetMinArg (-50.0);
    SetMaxArg (-18.0);
    SetMinFun (0.0);             //many points
    SetMaxFun (15.95123239744);  //[x=-25.132741228718345;y=-32.55751918948773] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = MathPow (f, 4);
    if (res < 0.0) res = 0.0;
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Megacity : public C_Function
{
  public: //===================================================================
  C_Megacity ()
  {
    SetNamFun ("Megacity");
    SetMinArg (-15.0);
    SetMaxArg (15.0);
    SetMinFun (0.0);   //many points
    SetMaxFun (15.0);  //[x=`3.16;y=1.990] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = floor (MathPow (f, 4));
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

Um die Gültigkeit der auf dem Prüfstand erzielten OA-Testergebnisse zu überprüfen, können wir ein Skript verwenden, das die X- und Y-Funktionen mit der Schrittweite aufzählt. Seien Sie vorsichtig bei der Wahl der Schrittweite, da eine sehr kleine Schrittweite dazu führt, dass die Berechnung zu lange dauert. Die Funktion Skin hat zum Beispiel den Argumentbereich [-5;5]. Mit dem Schritt von 0.00001 entlang der X-Achse, wird es (5-(-5))/0.00001=1'000'000 (Millionen) Schritte, die gleiche Zahl entlang der Y-Achse, bzw. die Gesamtzahl der Durchläufe der Testfunktion zur Berechnung des Wertes in jedem der Punkte wird gleich 1'000'000 х 1'000'000= 1'000'000'000'000 (10^12, Billion) sein.

Es ist wichtig zu verstehen, wie schwierig die Aufgabe für OA ist, da es erforderlich ist, das Maximum in nur 10'000 Schritten zu finden (ungefähr dieser Wert wird im MetaTrader 5 Optimizer verwendet). Vergessen wir nicht, dass diese Berechnung für eine Funktion mit zwei Variablen durchgeführt wird und die maximale Anzahl von Variablen, die in Tests verwendet werden, 1'000 beträgt.

Beachten Sie Folgendes: Die Algorithmentests in diesem und den folgenden Artikeln verwenden den Schritt 0,0 oder den kleinstmöglichen Schritt für eine bestimmte Implementierung der entsprechenden OA.

//——————————————————————————————————————————————————————————————————————————————
input EFunc  Function          = Skin;
input double Step              = 0.01;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  C_Function *TestFunc = SelectFunction (Function);

  double argMin = TestFunc.GetMinArg ();
  double argMax = TestFunc.GetMaxArg ();

  double maxFuncValue = 0;
  double xMaxFunc     = 0.0;
  double yMaxFunc     = 0.0;
  
  double minFuncValue = 0;
  double xMinFunc     = 0.0;
  double yMinFunc     = 0.0;
  
  double fValue       = 0.0;

  double arg [2];

  arg [0] = argMin;
  arg [1] = argMin;

  long cnt = 0;

  while (arg [1] <= argMax && !IsStopped ())
  {
    arg [0] = argMin;

    while (arg [0] <= argMax && !IsStopped ())
    {
      cnt++;

      fValue = TestFunc.CalcFunc (arg, 1);

      if (fValue > maxFuncValue)
      {
        maxFuncValue = fValue;
        xMaxFunc = arg [0];
        yMaxFunc = arg [1];
      }
      if (fValue < minFuncValue)
      {
        minFuncValue = fValue;
        xMinFunc = arg [0];
        yMinFunc = arg [1];
      }

      arg [0] += Step;
      
      if (cnt == 1)
      {
       maxFuncValue = fValue;
       minFuncValue = fValue;
      }
    }

    arg [1] += Step;
  }
  
  Print ("======", TestFunc.GetNamFun (), ", launch counter: ", cnt);
  Print ("MaxFuncValue: ", DoubleToString (maxFuncValue, 16), " X: ", DoubleToString (xMaxFunc, 16), " Y: ", DoubleToString (yMaxFunc, 16));
  Print ("MinFuncValue: ", DoubleToString (minFuncValue, 16), " X: ", DoubleToString (xMinFunc, 16), " Y: ", DoubleToString (yMinFunc, 16));
         
  delete TestFunc;
}

//——————————————————————————————————————————————————————————————————————————————

Schreiben wir unseren Prüfstand:

#include <Canvas\Canvas.mqh>
#include <\Math\Functions.mqh>
#include "AO_RND.mqh"

//——————————————————————————————————————————————————————————————————————————————
input int    Population_P       = 50;
input double ArgumentStep_P     = 0.0;
input int    Test1FuncRuns_P    = 1;
input int    Test2FuncRuns_P    = 20;
input int    Test3FuncRuns_P    = 500;
input int    Measur1FuncValue_P = 1000;
input int    Measur2FuncValue_P = 10000;
input int    NumberRepetTest_P  = 5;
input int    RenderSleepMsc_P   = 0;

//——————————————————————————————————————————————————————————————————————————————
int WidthMonitor = 750;  //monitor screen width
int HeighMonitor = 375;  //monitor screen height

int WidthScrFunc = 375 - 2;  //test function screen width
int HeighScrFunc = 375 - 2;  //test function screen height

CCanvas Canvas;  //drawing table
C_AO_RND AO;     //AO object

C_Skin       SkiF;
C_Forest     ForF;
C_Megacity  ChiF;

struct S_CLR
{
    color clr [];
};

S_CLR FunctScrin []; //two-dimensional matrix of colors
double ScoreAll = 0.0;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  //creating a table -----------------------------------------------------------
  string canvasName = "AO_Test_Func_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, WidthMonitor, HeighMonitor, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }
  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  ArrayResize (FunctScrin, HeighScrFunc);
  for (int i = 0; i < HeighScrFunc; i++)
  {
    ArrayResize (FunctScrin [i].clr, HeighScrFunc);
  }
  
  //============================================================================
  //Test Skin###################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (SkiF, Test1FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrLime);
  FuncTests (SkiF, Test2FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrAqua);
  FuncTests (SkiF, Test3FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrOrangeRed);
  
  //Test Forest#################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ForF, Test1FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrLime);
  FuncTests (ForF, Test2FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrAqua);
  FuncTests (ForF, Test3FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrOrangeRed);
  
  //Test Megacity#############################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ChiF, Test1FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrLime);
  FuncTests (ChiF, Test2FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrAqua);
  FuncTests (ChiF, Test3FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrOrangeRed);
  
  Print ("All score for C_AO_RND: ", ScoreAll / 18.0);
}
//——————————————————————————————————————————————————————————————————————————————

void CanvasErase ()
{
  Canvas.Erase (XRGB (0, 0, 0));
  Canvas.FillRectangle (1,                1, HeighMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
  Canvas.FillRectangle (HeighMonitor + 1, 1, WidthMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
}

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_Function &f,
                int        funcCount,
                double     minFuncVal,
                double     maxFuncVal,
                double     xBest,
                double     yBest,
                color      clrConv)
{
  DrawFunctionGraph (f.GetMinArg (), f.GetMaxArg (), minFuncVal, maxFuncVal, f);
  SendGraphToCanvas (1, 1);
  int x = (int)Scale (xBest, f.GetMinArg (), f.GetMaxArg (), 0, WidthScrFunc - 1, false);
  int y = (int)Scale (yBest, f.GetMinArg (), f.GetMaxArg (), 0, HeighScrFunc - 1, false);
  Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
  Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));
  Canvas.Update ();
  Sleep (1000);

  int xConv = 0.0;
  int yConv = 0.0;

  int EpochCmidl = 0;
  int EpochCount = 0;

  double aveMid = 0.0;
  double aveEnd = 0.0;

  //----------------------------------------------------------------------------
  for (int test = 0; test < NumberRepetTest_P; test++)
  {
    InitAO (funcCount * 2, f.GetMaxArg (), f.GetMinArg (), ArgumentStep_P);

    EpochCmidl = Measur1FuncValue_P / (ArraySize (AO.S_Colony));
    EpochCount = Measur2FuncValue_P / (ArraySize (AO.S_Colony));

    // Optimization-------------------------------------------------------------
    AO.F_EpochReset ();


    for (int epochCNT = 1; epochCNT <= EpochCount && !IsStopped (); epochCNT++)
    {
      AO.F_Preparation ();

      for (int set = 0; set < ArraySize (AO.S_Colony); set++)
      {
        AO.A_FFcol [set] = f.CalcFunc (AO.S_Colony [set].args, funcCount);
      }

      AO.F_Sorting ();

      if (epochCNT == EpochCmidl) aveMid += AO.A_FFpop [0];

      SendGraphToCanvas  (1, 1);

      //draw a population on canvas
      for (int i = 0; i < ArraySize (AO.S_Population); i++)
      {
        if (i > 0) PointDr (AO.S_Population [i].args, f.GetMinArg (), f.GetMaxArg (), clrWhite, 1, 1, funcCount);
      }
      PointDr (AO.S_Population [0].args, f.GetMinArg (), f.GetMaxArg (), clrBlack, 1, 1, funcCount);

      Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
      Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));

      xConv = (int)Scale (epochCNT,       1,          EpochCount, 2, WidthScrFunc - 2, false);
      yConv = (int)Scale (AO.A_FFpop [0], minFuncVal, maxFuncVal, 1, HeighScrFunc - 2, true);

      Canvas.FillCircle (xConv + HeighMonitor + 1, yConv + 1, 1, COLOR2RGB (clrConv));

      Canvas.Update ();
      Sleep (RenderSleepMsc_P);
    }

    aveEnd += AO.A_FFpop [0];

    Sleep (1000);
  }

  aveMid /= (double)NumberRepetTest_P;
  aveEnd /= (double)NumberRepetTest_P;

  double score1 = Scale (aveMid, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  double score2 = Scale (aveEnd, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  
  ScoreAll += score1 + score2;

  Print (funcCount, " ", f.GetNamFun (), "'s; Func runs ", Measur1FuncValue_P, " result: ", aveMid, "; Func runs ", Measur2FuncValue_P, " result: ", aveEnd);
  Print ("Score1: ", DoubleToString (score1, 5), "; Score2: ", DoubleToString (score2, 5));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void InitAO (const int    params,  //amount of the optimized arguments
             const double max,     //maximum of the optimized argument
             const double min,     //minimum of the optimized argument
             const double step)    //step of the optimized argument
{
  AO.F_Init (params, Population_P);
  for (int idx = 0; idx < params; idx++)
  {
    AO.A_RangeMax  [idx] = max;
    AO.A_RangeMin  [idx] = min;
    AO.A_RangeStep [idx] = step;
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void PointDr (double &args [], double Min, double Max, color clr, int shiftX, int shiftY, int count)
{
  double x = 0.0;
  double y = 0.0;
  
  double xAve = 0.0;
  double yAve = 0.0;
  
  int width  = 0;
  int height = 0;
  
  color clrF = clrNONE;
  
  for (int i = 0; i < count; i++)
  {
    xAve += args [i * 2];
    yAve += args [i * 2 + 1];
       
    x = args [i * 2];
    y = args [i * 2 + 1];
    
    width  = (int)Scale (x, Min, Max, 0, WidthScrFunc - 1, false);
    height = (int)Scale (y, Min, Max, 0, HeighScrFunc - 1, false);
    
    clrF = DoubleToColor (i, 0, count - 1, 0, 360);
    Canvas.FillCircle (width + shiftX, height + shiftY, 1, COLOR2RGB (clrF));
  }
  
  xAve /= (double)count;
  yAve /= (double)count;

  width  = (int)Scale (xAve, Min, Max, 0, WidthScrFunc - 1, false);
  height = (int)Scale (yAve, Min, Max, 0, HeighScrFunc - 1, false);

  Canvas.FillCircle (width + shiftX, height + shiftY, 3, COLOR2RGB (clrBlack));
  Canvas.FillCircle (width + shiftX, height + shiftY, 2, COLOR2RGB (clr));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void SendGraphToCanvas (int shiftX, int shiftY)
{
  for (int w = 0; w < HeighScrFunc; w++)
  {
    for (int h = 0; h < HeighScrFunc; h++)
    {
      Canvas.PixelSet (w + shiftX, h + shiftY, COLOR2RGB (FunctScrin [w].clr [h]));
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void DrawFunctionGraph (double     min,
                        double     max,
                        double     fMin,
                        double     fMax,
                        C_Function &f)
{
  double ar [2];
  double fV;

  for (int w = 0; w < HeighScrFunc; w++)
  {
    ar [0] = Scale (w, 0, HeighScrFunc, min, max, false);
    for (int h = 0; h < HeighScrFunc; h++)
    {
      ar [1] = Scale (h, 0, HeighScrFunc, min, max, false);
      fV = f.CalcFunc (ar, 1);
      FunctScrin [w].clr [h] = DoubleToColor (fV, fMin, fMax, 0, 250);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Scaling a number from a range to a specified range
double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0);
  else
  {
    if (Revers)
    {
      if (In < InMIN) return (OutMAX);
      if (In > InMAX) return (OutMIN);
      return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
    else
    {
      if (In < InMIN) return (OutMIN);
      if (In > InMAX) return (OutMAX);
      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color DoubleToColor (const double in,    //input value
                     const double inMin, //minimum of input values
                     const double inMax, //maximum of input values
                     const int    loH,   //lower bound of HSL range values
                     const int    upH)   //upper bound of HSL range values
{
  int h = (int)Scale (in, inMin, inMax, loH, upH, true);
  return HSLtoRGB (h, 1.0, 0.5);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color HSLtoRGB (const int    h, //0   ... 360
                const double s, //0.0 ... 1.0
                const double l) //0.0 ... 1.0
{
  int r;
  int g;
  int b;
  if (s == 0.0)
  {
    r = g = b = (unsigned char)(l * 255);
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
  else
  {
    double v1, v2;
    double hue = (double)h / 360.0;
    v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s));
    v1 = 2.0 * l - v2;
    r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0)));
    g = (unsigned char)(255 * HueToRGB (v1, v2, hue));
    b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0)));
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
}
//——————————————————————————————————————————————————————————————————————————————
//——————————————————————————————————————————————————————————————————————————————
double HueToRGB (double v1, double v2, double vH)
{
  if (vH < 0) vH += 1;
  if (vH > 1) vH -= 1;
  if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH);
  if ((2 * vH) < 1) return v2;
  if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6);
  return v1;
}
//——————————————————————————————————————————————————————————————————————————————

Um eine Zahl des Typs double aus einem Bereich in eine Farbe umzuwandeln, wurde der Algorithmus der Umwandlung von HSL in RGB verwendet (das Farbsystem von MetaTrader 5).

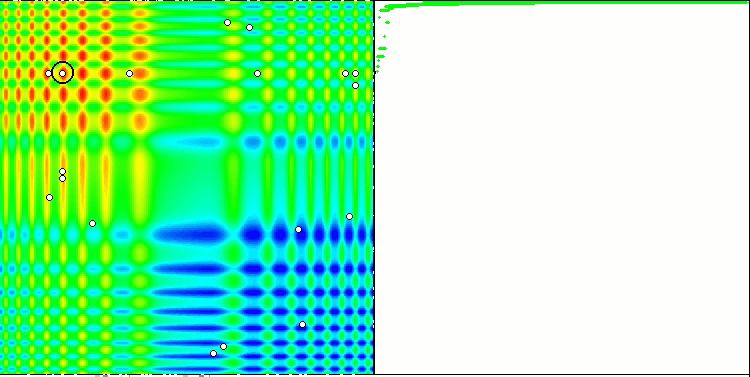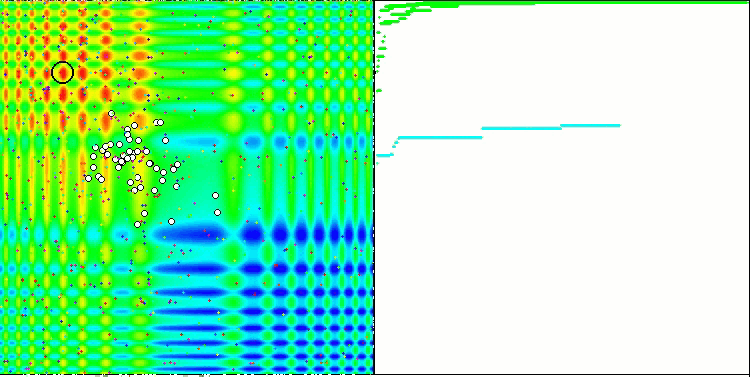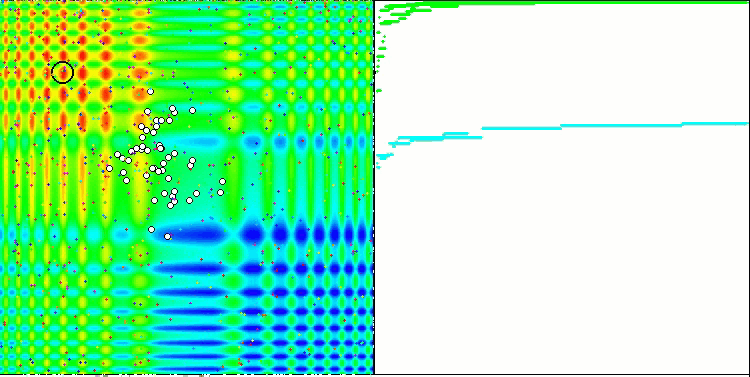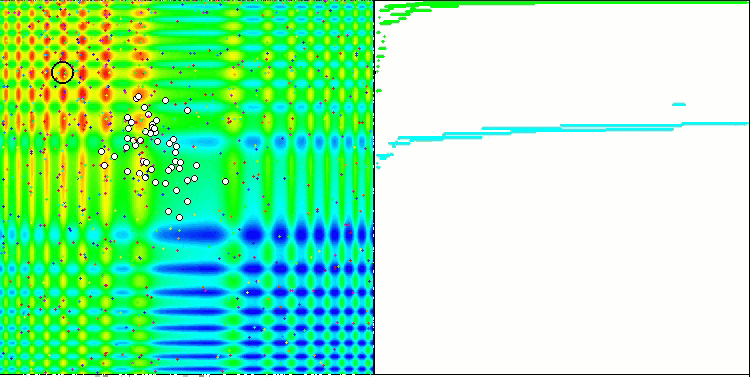
Der Prüfstand zeigt ein Bild in der Grafik an. Sie ist in zwei Hälften geteilt.

Die Testfunktion wird auf der linken Seite angezeigt. Der dreidimensionale Graph wird auf eine Ebene projiziert, wobei rot das Maximum und blau das Minimum bedeutet. Zeigt die Position der Punkte in der Grundgesamtheit an (die Farbe entspricht der Ordnungszahl der Testfunktion mit der Anzahl der Variablen 40 und 1000, bei einer Funktion mit zwei Variablen erfolgt keine Einfärbung), die Punkte, deren Koordinaten gemittelt werden, sind weiß markiert, während der beste Punkt schwarz markiert ist.
Das Konvergenzdiagramm wird auf der rechten Seite angezeigt, Tests mit 2 Variablen sind grün markiert, Tests mit 40 Variablen sind blau und Tests mit 1000 Variablen sind rot. Jeder der Tests wird fünfmal durchgeführt (5 Konvergenzdiagramme für jede Farbe). Hier können wir beobachten, wie sehr sich die Konvergenz von OA mit zunehmender Anzahl von Variablen verschlechtert.

6. Einfache OA mit RNG

Lassen Sie uns die einfachste Suchstrategie als Testbeispiel implementieren. Es hat keinen praktischen Wert, aber es wird in gewisser Weise ein Standard für den Vergleich von Optimierungsalgorithmen sein. Die Strategie erzeugt einen neuen Satz von Funktionsvariablen in einer 50/50-Zufallsauswahl: Entweder wird die Variable aus einem zufällig ausgewählten Elternsatz aus der Grundgesamtheit ausgewählt oder eine Variable aus dem Min/Max-Bereich erzeugt. Nach Erhalt der Werte der Testfunktionen wird der daraus resultierende neue Satz von Variablen in die zweite Hälfte der Grundgesamtheit kopiert und sortiert. So wird die eine Hälfte der Population ständig durch neue Sets ersetzt, während die besten Sets in der anderen Hälfte konzentriert sind.

Nachstehend finden Sie einen OA-Code, der auf RNG basiert:

//+————————————————————————————————————————————————————————————————————————————+
class C_AO_RND
{
  public: //||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

  struct ArrColony
  {
      double args [];
  };

  //----------------------------------------------------------------------------
  double    A_RangeStep []; //Step ranges of genes
  double    A_RangeMin  []; //Min ranges of genes
  double    A_RangeMax  []; //Max ranges of genes

  ArrColony S_Population []; //Population
  ArrColony S_Colony     []; //Colony

  double    A_FFpop [];      //Values of fitness of individuals in population
  double    A_FFcol [];      //Values of fitness of individuals in colony

  //----------------------------------------------------------------------------
  // Initialization of algorithm
  void F_Init (int argCount,       //Number of arguments

               int populationSize) //Population size
  {
    MathSrand ((int)GetMicrosecondCount ()); //reset of the generator

    p_argCount  = argCount;
    p_sizeOfPop = populationSize;
    p_sizeOfCol = populationSize / 2;

    p_dwelling  = false;

    f_arrayInitResize (A_RangeStep, argCount, 0.0);
    f_arrayInitResize (A_RangeMin,  argCount, 0.0);
    f_arrayInitResize (A_RangeMax,  argCount, 0.0);

    ArrayResize (S_Population, p_sizeOfPop);
    ArrayResize (s_populTemp, p_sizeOfPop);
    for (int i = 0; i < p_sizeOfPop; i++)
    {
      f_arrayInitResize (S_Population [i].args, argCount, 0.0);
      f_arrayInitResize (s_populTemp [i].args, argCount, 0.0);
    }

    ArrayResize (S_Colony, p_sizeOfCol);
    for (int i = 0; i < p_sizeOfCol; i++)
    {
      f_arrayInitResize (S_Colony [i].args, argCount, 0.0);
    }

    f_arrayInitResize (A_FFpop, p_sizeOfPop, -DBL_MAX);
    f_arrayInitResize (A_FFcol, p_sizeOfCol, -DBL_MAX);

    f_arrayInitResize (a_indexes, p_sizeOfPop, 0);
    f_arrayInitResize (a_valueOnIndexes, p_sizeOfPop, 0.0);
  }

  //----------------------------------------------------------------------------
  void F_EpochReset ()   //Reset of epoch, allows to begin evolution again without initial initialization of variables
  {
    p_dwelling = false;
    ArrayInitialize (A_FFpop, -DBL_MAX);
    ArrayInitialize (A_FFcol, -DBL_MAX);
  }
  //----------------------------------------------------------------------------
  void F_Preparation ();  //Preparation
  //----------------------------------------------------------------------------
  void F_Sorting ();      //The settling of a colony in population and the subsequent sorting of population

  private: //|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  //----------------------------------------------------------------------------
  void F_PopulSorting ();

  //----------------------------------------------------------------------------
  ArrColony          s_populTemp      []; //Temporal population
  int                a_indexes        []; //Indexes of chromosomes
  double             a_valueOnIndexes []; //VFF of the appropriate indexes of chromosomes

  //----------------------------------------------------------------------------
  template <typename T1>
  void f_arrayInitResize (T1 &arr [], const int size, const T1 value)
  {
    ArrayResize     (arr, size);
    ArrayInitialize (arr, value);
  }

  //----------------------------------------------------------------------------
  double f_seInDiSp         (double In, double InMin, double InMax, double step);
  double f_RNDfromCI        (double min, double max);
  double f_scale            (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);

  //---Constants----------------------------------------------------------------
  int  p_argCount;   //Quantity of arguments in a set of arguments
  int  p_sizeOfCol;  //Quantity of set in a colony
  int  p_sizeOfPop;  //Quantity of set in population
  bool p_dwelling;   //Flag of the first settling of a colony in population
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Preparation ()
{
  //if starts of algorithm weren't yet - generate a colony with random arguments
  if (!p_dwelling)
  {
    for (int person = 0; person < p_sizeOfCol; person++)
    {
      for (int arg = 0; arg < p_argCount; arg++)
      {
        S_Colony [person].args [arg] = f_seInDiSp (f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]),
                                                    A_RangeMin  [arg],
                                                    A_RangeMax  [arg],
                                                    A_RangeStep [arg]);
      }
    }

    p_dwelling = true;
  }
  //generation of a colony using with copying arguments from parent sets--------
  else
  {
    int parentAdress = 0;
    double rnd       = 0.0;
    double argVal    = 0.0;

    for (int setArg = 0; setArg < p_sizeOfCol; setArg++)
    {
      //get a random address of the parent set
      parentAdress = (int)f_RNDfromCI (0, p_sizeOfPop - 1);

      for (int arg = 0; arg < p_argCount; arg++)
      {
        if (A_RangeMin [arg] == A_RangeMax [arg]) continue;

        rnd = f_RNDfromCI (0.0, 1.0);

        if (rnd < 0.5)
        {
          S_Colony [setArg].args [arg] = S_Population [parentAdress].args [arg];
        }
        else
        {
          argVal = f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]);
          argVal = f_seInDiSp (argVal, A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]);

          S_Colony [setArg].args [arg] = argVal;
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Sorting ()
{
  for (int person = 0; person < p_sizeOfCol; person++)
  {
    ArrayCopy (S_Population [person + p_sizeOfCol].args, S_Colony [person].args, 0, 0, WHOLE_ARRAY);
  }
  ArrayCopy (A_FFpop, A_FFcol, p_sizeOfCol, 0, WHOLE_ARRAY);

  F_PopulSorting ();
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Ranging of population.
void C_AO_RND::F_PopulSorting ()
{
  //----------------------------------------------------------------------------
  int   cnt = 1, i = 0, u = 0;
  int   t0 = 0;
  double t1 = 0.0;
  //----------------------------------------------------------------------------

  // We will put indexes in the temporary array
  for (i = 0; i < p_sizeOfPop; i++)
  {
    a_indexes [i] = i;
    a_valueOnIndexes [i] = A_FFpop [i];
  }
  while (cnt > 0)
  {
    cnt = 0;
    for (i = 0; i < p_sizeOfPop - 1; i++)
    {
      if (a_valueOnIndexes [i] < a_valueOnIndexes [i + 1])
      {
        //-----------------------
        t0 = a_indexes [i + 1];
        t1 = a_valueOnIndexes [i + 1];
        a_indexes [i + 1] = a_indexes [i];
        a_valueOnIndexes [i + 1] = a_valueOnIndexes [i];
        a_indexes [i] = t0;
        a_valueOnIndexes [i] = t1;
        //-----------------------
        cnt++;
      }
    }
  }

  // On the received indexes create the sorted temporary population
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (s_populTemp [u].args, S_Population [a_indexes [u]].args, 0, 0, WHOLE_ARRAY);

  // Copy the sorted array back
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (S_Population [u].args, s_populTemp [u].args, 0, 0, WHOLE_ARRAY);

  ArrayCopy (A_FFpop, a_valueOnIndexes, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_RND::f_seInDiSp (double in, double inMin, double inMax, double step)
{
  if (in <= inMin) return (inMin);
  if (in >= inMax) return (inMax);
  if (step == 0.0) return (in);
  else return (inMin + step * (double)MathRound ((in - inMin) / step));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Random number generator in the custom interval.
double C_AO_RND::f_RNDfromCI (double min, double max)
{
  if (min == max) return (min);
  double Min, Max;
  if (min > max)
  {
    Min = max;
    Max = min;
  }
  else
  {
    Min = min;
    Max = max;
  }
  return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0)));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
double C_AO_RND::f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return (OutMIN);
    if (In > InMAX) return (OutMAX);
    return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
  }
}
//——————————————————————————————————————————————————————————————————————————————

7. Ergebnisse

AO	Durchläufe	Skin			Forest			Megacity (diskret)			Endgültiges Ergebnis
AO	Durchläufe	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	Endgültiges Ergebnis
RND	1000	0.98744	0.61852	0.49408	0.89582	0.19645	0.14042	0.77333	0.19000	0.14283	0.51254
RND	10,000	0.99977	0.69448	0.50188	0.98181	0.24433	0.14042	0.88000	0.20133	0.14283	0.51254

Nach den Tests auf dem Prüfstand fielen die Ergebnisse des RND OA ziemlich unerwartet aus. Der Algorithmus ist in der Lage, das Optimum von Funktionen mit zwei Variablen mit sehr hoher Genauigkeit zu finden, während im Falle von Forest und Megacity die Ergebnisse deutlich schlechter sind. Andererseits wurden meine Annahmen über schwache Sucheigenschaften für Funktionen mit vielen Variablen bestätigt. Die Ergebnisse sind schon bei 40 Argumenten sehr dürftig. Der endgültige kumulierte Wert ist 0.51254.

In den folgenden Artikeln werde ich bekannte und weit verbreitete Optimierungsalgorithmen analysieren und testen und die Ergebnistabelle, die das OA-Rating bildet, weiter ausfüllen.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8122

Beigefügte Dateien |

ZIP herunterladen

MQL5.zip (9.71 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 24): Herstellen eines robusten Systems (I)

In diesem Artikel werden wir das System zuverlässiger machen, um eine robuste und sichere Nutzung zu gewährleisten. Eine der Möglichkeiten, die gewünschte Robustheit zu erreichen, besteht darin, den Code so oft wie möglich wiederzuverwenden, damit er ständig in verschiedenen Fällen getestet wird. Aber das ist nur eine der Möglichkeiten. Eine andere Möglichkeit ist die Verwendung von OOP.

Risiko- und Kapitalmanagement durch Expert Advisor

In diesem Artikel geht es darum, was Sie in einem Backtest-Bericht nicht sehen können, was Sie erwarten sollten, wenn Sie automatisierte Handelssoftware verwenden, wie Sie Ihr Geld verwalten, wenn Sie Expert Advisors verwenden, und wie Sie einen erheblichen Verlust ausgleichen können, um in der Handelsaktivität zu bleiben, wenn Sie automatisierte Verfahren verwenden.

Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 25): Herstellen eines robusten Systems (II)

In diesem Artikel werden wir den letzten Schritt zu einem schnellen EA machen. Machen Sie sich also auf eine längere Lektüre gefasst. Um unseren Expert Advisor zuverlässig zu machen, werden wir zunächst alles aus dem Code entfernen, was nicht Teil des Handelssystems ist.

DoEasy. Steuerung (Teil 14): Neuer Algorithmus zur Benennung von grafischen Elementen. Fortsetzung der Arbeit am TabControl WinForms Objekt

In diesem Artikel werde ich einen neuen Algorithmus für die Benennung aller grafischen Elemente erstellen, die für die Erstellung von nutzerdefinierten Grafiken gedacht sind, sowie die Entwicklung des TabControl WinForms Objekts fortsetzen.