MetaTrader 5 / 統合
English Русский 中文 Español Deutsch Português
ディープニューラルネットワーク(その3)サンプル選択と次元削減

ディープニューラルネットワーク(その3)サンプル選択と次元削減

MetaTrader 5 — 統合 | 11 10月 2017, 15:08
2 464 0
Vladimir Perervenko
Vladimir Perervenko

内容

はじめに

本稿はニューラルネットワークの作業の最も重要な段階であるデータ準備を記述する3番目（そして最後）の記事です。ここでは、データを準備するための2つの非常に重要な手法を考察します。それらは、ノイズ除去と入力の次元削減です。手法の説明には、詳細な例とチャートが添付されます。

1. サンプル選択

訓練サンプルの間違ったラベル付けは「ノイズサンプル」と呼ばれ、非常に望ましくないデータの特殊性です。これを克服するためには、古典的かつ現代的なノイズフィルタを実装するNoiseFilterRパッケージを使用します。

最近、データマイニングは、データの特性に関連したますます複雑化する問題に対処しなければならなくなりました。問題はデータの量ではなく、その不完全さとさまざまな形が探検家にさまざまなシナリオを提示するということです。その結果、予備データ処理はKDD（Knowledge Discovery from Databases、データベースからの知識発見）過程の重要な部分となっています。同時に、予備データ処理のためのソフトウェアも開発され、作業に十分なツールを提供しています。

次のアルゴリズムがデータセットから最大の情報を抽出できるようにするには、予備データ処理が必要です。これは、KDDの全過程で最もエネルギー及び時間を擁する段階の1つです。予備データ処理は、サブタスクに分割することができます。例えば、これらは、予測変数の選択や欠落データとノイズデータの除去であり得ます。予測変数の選択は、訓練の最も重要な属性を抽出することを目的としており、モデルを単純化し計算時間を短縮することができます。可能な限り多くのデータを格納するには、欠落データの処理が必要です。ノイズデータとは、不正なデータか、データの分布から目立つデータです。

これらの問題はすべて、広く利用できるソフトウェアで解決できます。たとえば、KEEL (RKEEL)ツールには、前述のすべての操作をカバーする予備データ処理の幅広いアルゴリズムが含まれています。予測変数を選択するにはWEKA(RWEKA)やRapidMinerなどの他の一般的なソリューションもあります。また、R、KNIME、Pythonなどのデータマイニングのためのユニークなプログラム複合体も多数あります。

統計ソフトウェアRについては、包括的Rアーカイブネットワーク(Comprehensive R Archive Network、CRAN) に予備データ処理の問題を解決するためのパッケージが多数含まれています。

実際のデータセットは常に不完全でノイズが含まれています。このノイズは分類器の訓練に悪影響を及ぼして予測精度を低下させ、モデルを必要以上に複雑にして計算時間を増加させます。

分類に関する参考文献では、2つの異なるタイプのノイズ、すなわち属性ノイズとラベリングノイズ（またはクラスノイズ）が区別されています。前者は訓練データセット属性の不完全性によって生じ、後者は分類方法のエラーによって生じます。NoiseFiltersRパッケージは主にラベリングノイズに重点を置いています。ラベリングの品質は分類子の訓練に非常に重要であるため、ラベリングノイズは最も有害なものです。

ここでは、ノイズラベリングの問題を解決するための2つの主なアプローチが説明されています。Benoit FrenayとMichel Verleysenによる最近の取り組み（英語）ではこれを詳細に調べることができます。

  • 一方では、これは、ノイズの存在にあまり影響されない堅牢な分類アルゴリズムを作成することによって問題が解決される場合のアルゴリズムレベルでのアプローチです。この場合、各アルゴリズムは特定で普遍性にかけたものです。
  • 他方のデータレベルでのアプローチ（フィルタ）は、分類器を訓練する前に実行されるデータクリーニング戦略を開発する試みです。NoiseFiltersRパッケージは2番目の方法を利用しています。これは、予備データ処理を1回だけしか実行できず分類器は必要な回数だけ変更することができるためです。

С4.5、J48、Jrip (WEKA)の各分類器はノイズに強いものです。

実験をしてみましょう。DT（前処理前の生データ）、DTn（正規化された生データセットのみ）、DTTanh.n（外れ値なし、tan変換及び正規化）、 ノイズを除去するためのフィルタであるORBoostFilter()関数を使用した訓練セットのデータセットを処理し、このような処理の後に分布がどのように変わったかを見てみましょう。

evalq({
  #-----DT---------------------
  out11 <- ORBoostFilter(Class~., data = DT$train, N = 10, useDecisionStump = TRUE)
  DT$train_clean1 <- out11$cleanData
  #----------DTTanh.n------------------------
  out1 <- ORBoostFilter(Class~., data = DTTanh.n$train, N = 10, useDecisionStump = TRUE)
  DTTanh.n$train_clean1 <- out1$cleanData
  #-----------DTn--------------------------------
  out12 <- ORBoostFilter(Class~., data = DTn$train, N = 10, useDecisionStump = TRUE)
  DTn$train_clean1 <- out12$cleanData
},
env)
#---Ris1-----------------
require(funModeling)
evalq({
  par(mfrow = c(1,3))
  par(las = 1)
  boxplot(DT$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DT$train_clean1")
  boxplot(DTn$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DTn$train_clean1")
  boxplot(DTTanh.n$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DTTanh.n$train_clean1")
  par(mfrow = c(1,1))
}, env)

ТА9

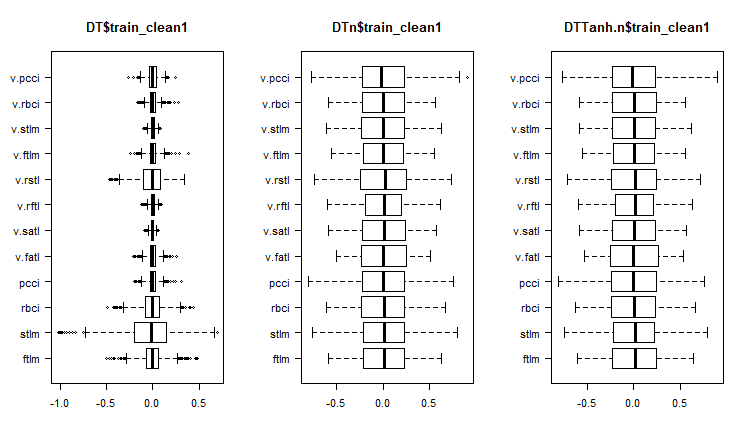
図1　ノイズサンプルを除去した後のセット内の予測変数の分布

これらのセットにどのような変動と共分散があるかを見てみましょう。

#----Ris2------------------
require(GGally)
evalq(ggpairs(DT$train_clean1 %>% select(-Data), 
              columns = c(1:6, 13), 
              mapping = aes(color = Class),
              title = "DT$train_clean1/1"), 
      env)

NF2

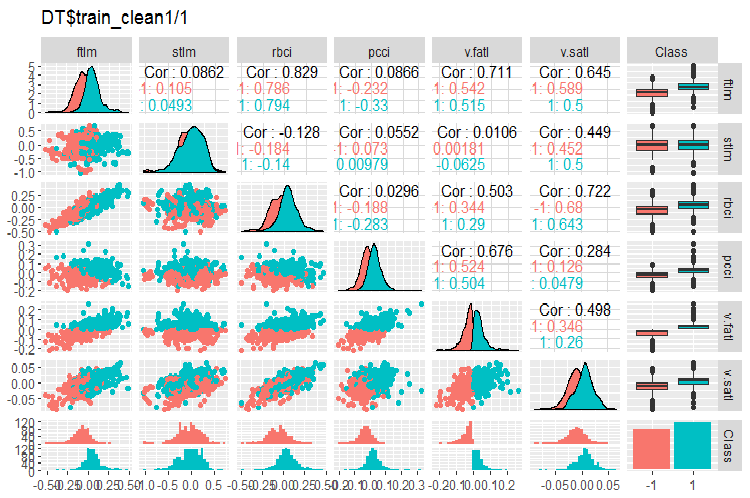
図2　ノイズサンプルを除去した後のDT$train_clean1/1セット内の変動と共分散

#-----Ris3---
evalq(ggpairs(DT$train_clean1 %>% select(-Data), 
              columns = 7:13, 
              mapping = aes(color = Class),
              title = "DT$train_clean1/2"), 
      env)

NF3

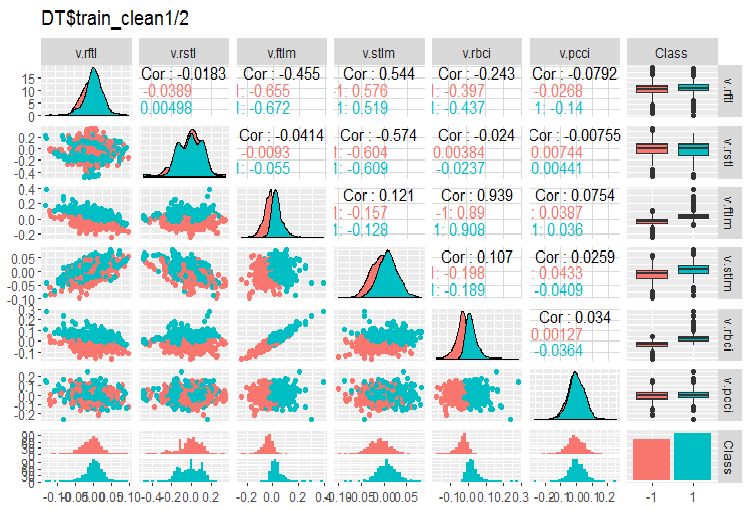
図3　ノイズサンプルを除去した後のDT$train_clean1/2セット内の変動と共分散

DT$trainセットからはいくつのサンプルが除去されたのでしょうか。

> env$out11$remIdx %>% length()
[1] 658

これはおよそ30%です。やり方は2つあります。1番目は、訓練セットからノイズサンプルを除去してモデルの訓練に使うことです。 2番目は、それらを新しいクラスラベルで再編成し、モデルを完全な訓練モデルで、目標変数の1つの追加レベルで訓練することです。このノイズサンプルの多さでは、2番目のシナリオがより望ましく思えます。テストしましょう。

ノイズなしの可変分布のチャートでは何が分かるでしょうか。

  1. 目標変数による予測変数の分布の特徴的な区分 - これにより、訓練中のモデルの精度が大幅に向上する可能性が高くなる
  2. ほぼすべての外れ値が除去されている

フィルタを使用してDTn$train DTTanh.n$train訓練データセットをクリーンします。最初の場合と同じくらい多くのノイズ変数があることに驚かれるでしょう。 

c(env$out1$remIdx %>% length(), env$out12$remIdx %>% length())
[1] 652 653

これは変換がノイズサンプルを有用にしないことを意味するのでしょうか。テストの価値があります。

ノイズ変数を除去した後のDTTanh.n$trainセットの変動と共分散を見てみましょう。

#----Ris4-----------------------
evalq(ggpairs(DTTanh.n$train_clean1, columns = 1:13, 
              mapping = aes(color = Class),
              upper = "blank",
              title = "DTTanh.n$train_clean_all"), 
      env)

NF6


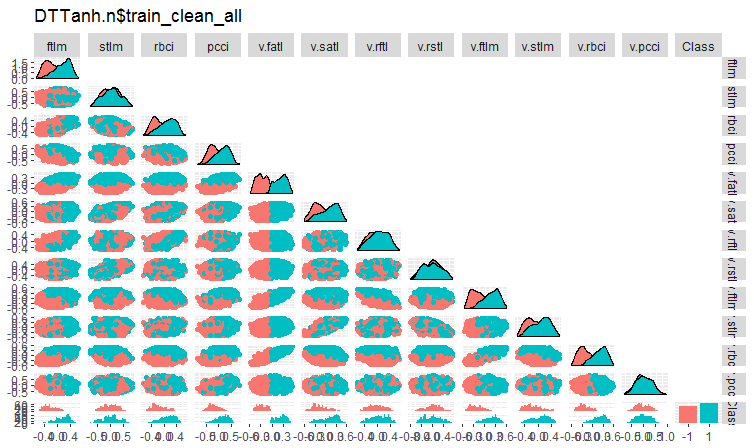
図4　ノイズサンプルを除去した後のDTTanh.n$train_cleanセット内の変動と共分散

全ての変数とv.fatl.変数との共分散は非常に興味深いです。目標変数とは無関係の予測変数stlm、v.rftl、v.rstl、v.pcciが視覚的に特定されています。この仮定を、別のセットの他のメソッドを使用してテストします。

DTn$train_clean1での同じチャートは下記です。

#-------ris5----------
require(GGally)
evalq(ggpairs(DTn$train_clean1 %>% select(-Data), 
              columns = 1:13, 
              mapping = aes(color = Class),
              upper = "blank",
              title = "DTn$train_clean1_all"), 
      env)

NF7

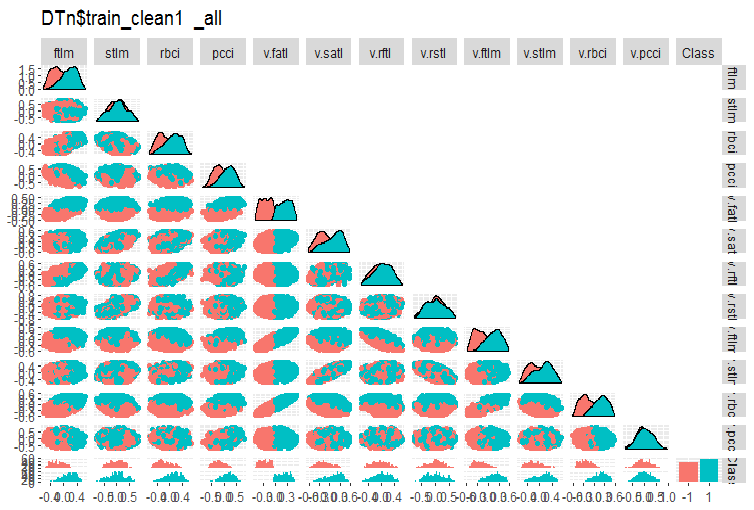
図5　ノイズサンプルを除去した後のDTn$train_cleanセットの変動と共分散

ここでは、stlm、v.rftl、v.rstl、v.pcci予測変数の変動が目標変数のレベルで分かれていないことがわかります。モデル訓練の実験を行った後にノイズ変数を使って何をすべきかを決定するのは開発者次第です。

ここで、ノイズサンプルが除去された後、これらのデータセットで予測変数の重要性がどのように変化したかを見てみましょう。 

#--------Ris6---------------------------
require(smbinning)
par(mfrow = c(1,3))
evalq({
  df <- renamepr(DT$train_clean1) %>% targ.int
  sumivt.dt = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.dt, cex = 0.8)
  rm(df)
}, 
env)
evalq({
  df <- renamepr(DTTanh.n$train_clean1) %>% targ.int
  sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.8)
  rm(df)
}, 
env)
evalq({
  df <- renamepr(DTn$train_clean1) %>% targ.int
  sumivt.dtn = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.dtn, cex = 0.8)
  rm(df)
}, 
env)
par(mfrow = c(1, 1))

NF8

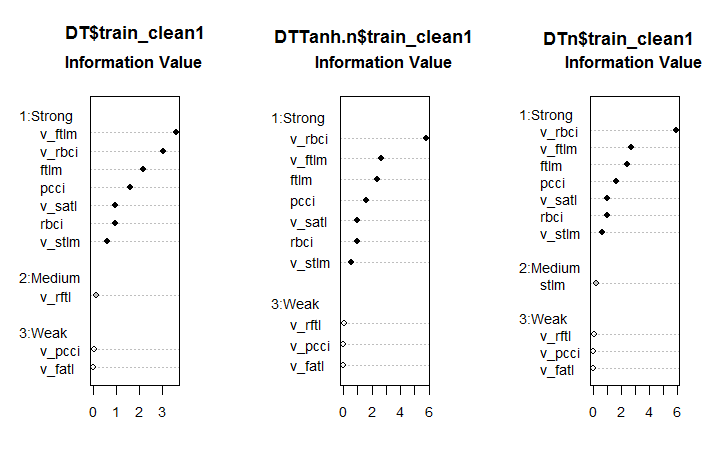
図6　3セットでの予測変数の重要性

これは予想外の結果です。v.fatl変数が最も弱いことが判明したのです。

7つの強い予測変数はすべてのセットで同じです。第1セットと第3セットには中位の強さを持つ1つの予測変数がありました。この計算によってstlm、v.rftl、v.rstl、v.pcci 予測変数が無関係であることが識別されました。これは以前の計算と一致しています。これらの計算はすべて、実際のモデルによる実験によって検証されなければなりません。

NoiseFilterRパッケージには、ノイズサンプルを識別するための12個以上のフィルタがあります。頑張って実験してください。

2. 次元削減

次元削減とは、主要な情報を保持しながら、より高次元を持つ初期データをより低次元の新しい表現に変換することです。理想的には、変換された表現の次元はデータの内部次元と等しいものです。データの内部次元は、データのすべての可能な特性を表現するために必要な変数の最小数です。主成分分析(PCA)、独立成分分析(ICA)、特異値分解(SVD)などは、次元を減らすために伝統的に使用されているアルゴリズムです。

次元削減は、いわゆる「次元の呪い」などの高次元空間の望ましくない特徴の緩和を可能にします。データ記述の段階には、次の目的があります。

  • データ処理中の計算コストを削減する。
  • 再訓練の必要性を減らす。特徴の数が少ないほど、データ内の隠れた関係の堅牢な復元に必要なオブジェクトが少なくなり、そのような関係の復元の品質が向上する。
  • 情報をより効率的に保管するためにデータを圧縮する。そのような場合、変換X→Tとともに、逆変換T→Xを実行する機会が必要である。
  • データの可視化。サンプルを2次元または3次元空間に投影することで、このサンプルをグラフィカルに表現することができる。
  • 新しい特徴の抽出。X → T変換の間に得られた新しい特徴は、認識のための解決法（例えば、主成分分析など）の次の実装の間に重要な影響を及ぼし得る。

以下で簡単に説明する次元削減のすべての手法は、教師なしの訓練のクラスに属することにご注意ください。これは、オブジェクトX（予測変数）の特徴記述のみが初期情報の役割を果たすことを意味します。

2.1. 主成分分析(Principal Component Analysis、PCA)

主成分分析(Principal component analysis、PCA)は、データ次元削減の最も簡単な手法です。この手法の主なアイデアの出現は19世紀にさかのぼります。この手法の原則は、最初の空間である次元の超平面を見つけて、この超平面にデータセットを投影することです。投影データの誤差が最小である超平面（偏差の二乗の和）が選択されます。

削減された空間の次元性d は、ユーザが予め設定することができます。この値は、データを視覚化する（d = 2またはd = 3）問題やセットメモリーにデータセットを入れる問題では容易に選択できます。他の場合では、dの選択は前提条件からは明らかではありません。

主成分法ではdの値を選択する簡単なヒューリスティックな手法があります。主成分法の特異性の1つは、d = 1、2、. . の全ての削減された空間が互いに挿入されることです。これによって、共分散行列のすべての固有ベクトルと固有値が計算されると、任意のd値に対して削減された空間を取得することができます。したがって、d値を選択するには、固有値を降順でチャートに表示し、カットオフ閾値を設定してゼロとはほとんど異なる値が右側に表示されるようにすることができます。d値を選択するもう1つの方法は、曲線の下の総面積の特定の割合が右側にあるように（たとえば5％または1％）閾値を選択することです。

簡単に言えば、PCAは、その数が有意(>50)であれば、ノイズ予測変数を予備的に抑制するのに使うことができます。

2.2. 独立成分分析(Independent Component Analysis、ICA)

独立成分分析はPCAとは異なって最近出現しましたが、データ探査のさまざまな分野で急速に普及しています。

主成分分析とは異なり、ICA変換にはモデルが必要です。最も一般的なモデルは、P変数が独立変数の線形変換pから測定されるという仮定です。ICAの目的は、初期独立変数を復元することです。ICAアルゴリズムの大部分は、最初にデータの白色化を可能にし、その結果データを可能な限り独立させるようにデータを回転させます。成分が順番に構築されるときは、以前に選ばれた投影に接続されていない大きな非ガウス投影を検索することを意味します。

独立成分法は、信号処理中に広く使用されています。この技術は、初期データを新しい成分に線形変換します。新しい成分は、可能な限り統計的に独立しています。独立成分は必ずしも直交しませんが、その統計的独立性は、PCAにおける統計的相関の欠如よりも厳しい条件です。

caretパッケージでは、PCA及びICAメソッドはpreProcess()関数によって実装されます。この関数では、主成分の数またはPCAでカバーされる分散の累積パーセントを設定できます。独立成分分析には2つの段階があります。まず、必要なパラメータが訓練データセットで計算されます。次に、データセットと後で入る新しいデータがすべてpredict()を使用して変換されます。

表1　PCAとICAの比較特性

 手法長所
 短所特色
 ほとんどの場合得られる結果
 新しい主成分を計算する方
 PCA 計算の
簡易さ
  • 変換の線形性
  • 外れ値に対する高感度
  • NAを受け入れない
  解の非一意性（回転不確実性） - 1つの訓練テストに基づく新しい計算ごとに異なる主成分が生成される
 
  • Т — 次元[I×A]のスコア行列 (scores)
  • P — 次元[J×A]の荷重行列 (loadings) Х[、J]空間からPCA [A]への遷移行列
  • E — E - 次元を持つ剰余の行列[I x J]
 Tnew = Xnew * P
ICA
計算の簡易さ
  • データの強制的な標準化
  • 変換の線形性
  • 外れ値に対する高感度
  • NAを受け入れない
  • 2 - 5成分に適応
入力データセットと独立した成分の次元が大きく異なるためPCA→ICAが連続して使用される
  • W — 除算行列
  • K — 白色化前の行列
 Snew =scale( Xnew )* W * K

実験をしてみましょう。スクリプト計算の結果を記事Part_1.Rdaの最初の部分からRstudioに読み込みます。以下はenvの内容です。

> ls(env)
 [1] "cap1"         "cap2"         "Close"        "Data"         "dataSet"     
 [6] "dataSetCap"   "dataSetClean" "dataSetOut"   "High"         "i"           
[11] "k"            "k.cap"        "k.out"        "lof.x"        "lof.x.cap"   
[16] "Low"          "lower"        "med"          "Open"         "out.ftlm"    
[21] "out.ftlm1"    "pr"           "pre.outl"     "preProClean"  "Rlof.x"      
[26] "Rlof.x.cap"   "sk"           "sk.cap"       "sk.out"       "test"        
[31] "test.out"     "train"        "train.out"    "upper"        "Volume"      
[36] "x"            "x.cap"        "x.out"
補完された外れ値を持つx.capデータセットをとってpreProcess::caret関数でその原則と独立成分を計算します。PCAとICAの成分数を明示的に指定します。ICAの正規化の手法は指定しません。 
require(caret)
evalq({
  prePCA <- preProcess(x.cap, 
                       pcaComp = 5,
                       method = Hmisc::Cs(center, scale, pca))
  preICA <- preProcess(x.cap,
                       n.comp = 3, 
                       method = "ica")
}, env)
変換のパラメータを見てみましょう。
> str(env$prePCA)
List of 20
 $ dim              : int [1:2] 7906 11
 $ bc               : NULL
 $ yj               : NULL
 $ et               : NULL
 $ invHyperbolicSine: NULL
 $ mean             : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ std              : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ ranges           : NULL
 $ rotation         : num [1:11, 1:5] -0.428 -0.091 -0.437 -0.107 -0.32 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
 $ method           :List of 4
  ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ pca   : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ ignore: chr(0) 
 $ thresh           : num 0.95
 $ pcaComp          : num 5
 $ numComp          : num 5
 $ ica              : NULL
 $ wildcards        :List of 2
  ..$ PCA: chr(0) 
  ..$ ICA: chr(0) 
 $ k                : num 5
 $ knnSummary       :function (x, ...)  
 $ bagImp           : NULL
 $ median           : NULL
 $ data             : NULL
 - attr(*, "class")= chr "preProcess"

ここで興味深いのはprePCA$mean、prePCA$std （正規化パラメータ）、prePCA$rotation（回転と荷重の行列）の3つのスロットです。

> str(env$preICA)
List of 20
 $ dim              : int [1:2] 7906 11
 $ bc               : NULL
 $ yj               : NULL
 $ et               : NULL
 $ invHyperbolicSine: NULL
 $ mean             : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ std              : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ ranges           : NULL
 $ rotation         : NULL
 $ method           :List of 4
  ..$ ica   : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ ignore: chr(0) 
 $ thresh           : num 0.95
 $ pcaComp          : NULL
 $ numComp          : NULL
 $ ica              :List of 3
  ..$ row.norm: logi FALSE
  ..$ K       : num [1:11, 1:3] -0.214 -0.0455 -0.2185 -0.0534 -0.1604 ...
  ..$ W       : num [1:3, 1:3] -0.587 0.77 -0.25 -0.734 -0.636 ...
 $ wildcards        :List of 2
  ..$ PCA: chr(0) 
  ..$ ICA: chr(0) 
 $ k                : num 5
 $ knnSummary       :function (x, ...)  
 $ bagImp           : NULL
 $ median           : NULL
 $ data             : NULL
 - attr(*, "class")= chr "preProcess"
ここでは、同じ$meanと$stdと2つの行列$K$Wがあります。ICAを計算するcaret パッケージは次のアルゴリズムでfastICAパッケージを使用します。
  • 初期行列が中心に置かれた後（行の正規化が可能）に行列Xを取得する
  • 行列は主成分の方向に投影され、結果としてPCA = X * Kが得られる
  • その後、PCAには非混合行列が乗算され、ICA = X * K * W独立成分が得られる

predict::caret関数とpreProcess関数で得られたパラメータを使って、PCAとICAを2通りの方法で計算しましょう。

require(magrittr)
evalq({
  pca <- predict(prePCA, x.cap)
  ica <- predict(preICA, x.cap)
  pca1 <- ((x.cap %>% scale(prePCA$mean, prePCA$std)) %*% 
                   prePCA$rotation) 
  ica1 <- ((x.cap %>% scale(preICA$mean, preICA$std)) %*% 
                   preICA$ica$K) %*% preICA$ica$W
  colnames(ica1) <- colnames(ica1, do.NULL = FALSE, prefix = 'ICA')
    
},env)
evalq(all_equal(pca, pca1), env)
# [1] TRUE
evalq(all_equal(ica, ica1), env)
# [1] TRUE

結果は同じで、予想通りでした。

PCA計算においてより信頼性の高いのはpcaPPパッケージを使用した方法です。この方法では、主成分がより正確に識別されます。

fastICAパッケージには、独立成分をより柔軟で完全に計算するための多くの追加機能とパラメータが含まれています。caretの関数の代わりにfastICAを使用するようお勧めします。

2.3確率的主成分分析(Probabilistic principal component analysis、PPCA)

PCAには確率モデルがあります。PPCAです。この手法を確率論的に言い換えると、多くの利点が得られます。

  • 解を検索するためにЕМアルゴリズムを使用する機会 - ЕМアルゴリズムは、d ≪ Dのときにより効果的な計算手順である
  • 欠損値の処理の修正 - それらは単に確率モデルの隠れ変数のリストに追加され、次に、ЕМアルゴリズムがこのモデルに適用される
  • 手法の適用性を広げる混合分布のモデルへの移行の可能性
  • ベイズアプローチを使用してモデルを選択する問題を解決する可能性 - 特に、削減された空間の次元dを選択する理論的に正当化されたスキームを構築することが可能（[24,25]を参照）
  • 確率モデルから新しいオブジェクトを生成する可能性
  • 分類 - 分類スキームでのさらなる使用のために別々のオブジェクトクラスの分布をモデル化する可能性
  • 尤度関数の値は、異なる確率モデルの相互比較を可能にする普遍的な基準である。具体的には、データセット内の外れ値は、尤度値を使用して容易に識別可能

PCAの古典的モデルと同様に、確率モデルPCAは、超平面における基底の選択に関して不変です。

PCAの古典的モデルとは異なり、すべてのデータの中で最良のものを説明する超平面のみが復元される確率モデルは、データ変動のモデル全体を復元します。すなわち、あらゆる方向のデータ分散が記述されます。したがって、解には、共分散行列の固有ベクトルによって定義される超平面の方向基底ベクトルだけでなく、これらの基底ベクトルの長さも含まれます。

РРСАを使用して、主成分化合物を得る他の非線形方法を使用するにはpcaMethodsパッケージを使用することができます。

pcaMethodsパッケージは、交差検証と結果の視覚化のためのさまざまなPCAとツールを実装したものです。メソッドでは、主に不完全なデータセットにPCAを適用することができ、欠損値（NA）の評価に使用することができます。パッケージはリポジトリのBioconductorにあり、以下のようにインストールできます。

source("https://bioconductor.org/biocLite.R")
biocLite("pcaMethods")
library(pcaMethods)

パッケージのすべてのメソッドは、結果を含む汎用クラスpcaResを返します。これにより、ユーザは良好な柔軟性を得ることができます。pca() ラッパー関数は、命名引数を使ってすべての必要な型のРСАへのアクセスを可能にします。以下に簡単な説明を含むアルゴリズムのリストを示します。

  • svdPCAはprcomp標準関数のラッパー関数である
  • svdImputeはNAを補完するためのアルゴリズムの実装でNAの高値(>10%)に耐性がある
  • 確率的PCA(ppca)には、10％〜15％の間のNAに耐性がある
  • ベイジアンPCA (bpca)は確率的PCAと似ており、値を復元する確率を計算するためにベイジアンモデルでEMアプローチを使用し、アルゴリズムは比較的多数 (>10%)の欠落データに耐性がある。この手法で得られたスコアと荷重は、通常のРСАで得られたスコアと荷重とは異なる。これは、BPCAが欠損値の評価のために特別に開発され、自動関連性識別（ARD）を使用したバリエーションベイジアンフレームワーク（VBF）に基づいているという事実に関連している。このアルゴリズムは荷重間の直交性を強制しない。事実、BPCAの著者たちは、直交性基準を含むと予測が悪化することを発見した。
  • 逆非線形PCA（NLPCA）は、予測変数と目標変数の関係が非線形である実験データに最適である。NLPCAは、連想型ニューラルネットワーク（自己符号化器）の復号化部分の訓練に基づいており、負荷はネットワークの隠れ層で見ることができる。訓練データの欠損値は、逆伝播中のエラー計算で無視される。このように、NLPCAは標準のРСАと同じ方法で欠損値の処理に使用でき、唯一の違いは、荷重Pがニューラルネットワークによって表されることである。このような次元削減法については「自己符号化器」節で詳しく説明される。
  • Nipals PCAは反復部分最小二乗法による非線形評価です。これはPLS回帰の中核となるアルゴリズムであり、欠損値を有するPCAをそれぞれの内部生成物の外側に残すことができる。少数（通常は5％以下）の欠損データには耐性がある。
  • 局所最小二乗（LLS）代入 は、不完全な変数のk近傍点の線形結合に基づいて欠損値を評価するllsImpute()アルゴリズム/関数である。変数間の距離は、Pearson、SpearmanまたはKendall相関係数の絶対値として定義される。最適な線形結合は、最小自乗の局所問題を解くことによって見つけることができる。

現在の実装では、欠損値を評価する2つの方法が提示されており、違いはわずかです。1番目の方法は、すべての変数のサブセットによる近隣探索の制限です。この方法は、未定義変数の数がかなり少ない場合に適しています。2番目の方法はすべての変数を候補とみなします。ここでは、欠落値は最初に列の平均で置き換えられます。次に、この方法は、新しい評価値と古い評価値との違いが特定の閾値 (0,001)を下回るまで、現在の評価値をLLS回帰の入力として使用して反復します。

残念ながら、本稿の本題と長さでは、この素晴らしいパッケージのすべての推奨アルゴリズムについて書くことはできません。NLPCAは後で自己符号化器と比較して見るだけにします。

2.4. 自己符号化器

自動連想ネットワークはディープニューラルネットワークの登場から広く使用されてきました。オートスケジューリング自己符号化器（АЕ）、スタック自己符号化器、制限付きボルツマンマシン（RBM）などの構造と特性は前の記事のうちの1つで詳しく検討しました。

自己符号化器は、1つまたは複数の隠れ層を持ち、入力層のニューロンの数が出力層のニューロンの数に等しいニューラルネットワークです。АЕの主な目的は、入力データを可能な限り正確に表現することで、標準的なニューラルネットワークに使用されている訓練、正則化、及びニューロン活性化の同じ手法がAEでも使用されます。AEのモデルは、隠れ層重みの行列を抽出することを可能にする、ニューラルネットワークを構築するための任意のパッケージを使用して構築することができます。これにはautoencoderパッケージを使用します。以下の例は、可能なAE構造を思い出すのに役立つでしょう。

AE_1

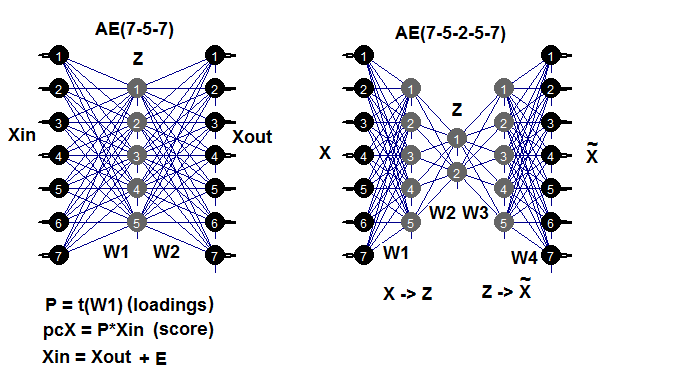
図7　自動エンコーダの構造図（3層及び5層）

第1層（入力層）と隠れ層との間の重み行列 W1 は、訓練の結果として得られる荷重です。入力行列Xinを荷重に投射（乗算）すると縮小行列（本質的に主成分）が得られます。predict()を使用しても同じ結果が得られます。この関数は、隠し層の出力（hidden.output = TRUEの場合）または自動エンコーダの出力層（hidden.output = FALSEの場合）のいずれかを取得することを可能にします。

AEを訓練すると、重み行列W1とモデルからの回復誤差を抽出することができます。テストデータセットを入力して、モデルからテストエラーを取得することもできます。訓練の誤差はAEのパラメータに大きく左右されますが、それ以上にn.hidden/n.in比に大きく左右されます。この比が大きいほど、回復誤差が大きくなります。重要な次元削減を達成することを目指すと、2つのAEを結びつけることができます。たとえば、12の入力がある場合はモデル12-7-12を訓練することができます。隠れ層からpredict()を実行し、自己符号化器7-3-7に入力します。削減は12 - > 3になります。頑張って実験してください。

このパッケージは多層AEを作成して訓練する能力を持ちますが、個人的にこれを使うことができなかったことには言及するべきです。

実験をしてみましょう。本稿冒頭の計算結果を持つ Part_1.RDataが既に存在します。以下は計算のシーケンスです。

  • dataSetセットから訓練/テスト/検証データセットを作成し、DTリストを取得する。
  • 外れ値を補完してDTcapリストを取得する。
  • （ "center"、 "scale"、 "spatialSign"）メソッドを使用して、セットを連続的に正規化する。これまでに考察した変換と正規化の他の方法を使うことができる。
  • 隠れ層に3つのニューロンを持つ自己符号化器モデルを訓練する。他のバリアントを調べることもできる。隠れニューロンの数が増加すると、回復エラーは減少する。
  • 訓練されたモデルとpredict()を使用して、隠れ層から結果を取得する。これは本質的には縮小マトリックス (РСА)である。目標変数を追加する。
  • 縮小されたサンプル訓練/テスト/検証の変動と共分散のチャートをプロットする。 
require(FCNN4R)
require(deepnet)
require(darch)
require(tidyverse)
require(magrittr)
#----クリーン---------------------
require(caret)
require(pipeR)
evalq(
  {
    train = 1:2000
    val = 2001:3000
    test = 3001:4000
    DT <- list()
    dataSet %>%
      preProcess(., method = c("zv", "nzv", "conditionalX")) %>%
      predict(., dataSet) %>%
      na.omit -> dataSetClean
    list(train = dataSetClean[train, ], 
         val = dataSetClean[val, ], 
         test = dataSetClean[test, ]) -> DT
    rm(dataSetClean, train, val, test)
  }, 
  env)
#------外れ値-------------
require(foreach)
evalq({
  DTcap <- list()
  foreach(i = 1:3) %do% {
    DT[[i]] %>% 
      select(-c(Data, Class)) %>%
      as.data.frame() -> x
    if (i == 1) {
      foreach(i = 1:ncol(x), .combine = "cbind") %do% {
        prep.outlier(x[ ,i]) %>% unlist()
      } -> pre.outl
      colnames(pre.outl) <- colnames(x)
    } 
    foreach(i = 1:ncol(x), .combine = "cbind") %do% {
      stopifnot(exists("pre.outl", envir = env))
      lower = pre.outl['lower.25%', i] 
      upper = pre.outl['upper.75%', i]
      med = pre.outl['med', i]
      cap1 = pre.outl['cap1.5%', i] 
      cap2 = pre.outl['cap2.95%', i] 
      treatOutlier(x = x[ ,i], impute = T, fill = T, 
                   lower = lower, upper = upper, 
                   med = med, cap1 = cap1, cap2 = cap2) 
    } %>% as.data.frame() -> x.cap
    colnames(x.cap) <- colnames(x)
    return(x.cap)
  } -> DTcap
  foreach(i = 1:3) %do% {
    cbind(DTcap[[i]], Class = DT[[i]]$Class)
  } -> DTcap
  DTcap$train <- DTcap[[1]]
  DTcap$val <- DTcap[[2]]
  DTcap$test <- DTcap[[3]]
  rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
#------正規化-----------
evalq(
  {
    method <- c("center", "scale", "spatialSign") #, "expoTrans") #"YeoJohnson", 
                                                 # "spatialSign"
    preProcess(DTcap$train, method = method) -> preproc 
    list(train = predict(preproc, DTcap$train), 
         val = predict(preproc, DTcap$val),
         test = predict(preproc, DTcap$test)
    ) -> DTcap.n
    #foreach(i = 1:3) %do% {
    #  cbind(DTcap.n[[i]], Class = DT[[i]]$Class)
    #} -> DTcap.n
  }, 
  env) 
#----訓練-------
require(autoencoder)
evalq({
  train <-  DTcap.n$train %>% select(-Class) %>% as.matrix()
  val <-  DTcap.n$val %>% select(-Class) %>% as.matrix()
  test <-  DTcap.n$test %>% select(-Class) %>% as.matrix()
  ## 自己符号化器のアーキテクチャを設定する
  nl = 3                    ## number of layers (default is 3: input, hidden, output)
  unit.type = "tanh"        ## specify the network unit type, i.e., the unit's 
   ## アクティブ化関数 ("logistic"または"tanh")
  N.input = ncol(train)   ## 入力層でのユニット（ニューロン）数（画素当たり1ユニット）
  N.hidden = 3              ## 隠れ層のユニット数
  lambda = 0.0002           ## 重み減衰パラメータ     
  beta = 0                  ## スパース・ペナルティ・タームの重み 
  rho = 0.01                ## 所望のスパース性パラメータ
  epsilon <- 0.001          ## 重み初期化のための小さいパラメータ 
   ## Nからサンプリングされた小さなガウス乱数として(0,epsilon^2)
  max.iterations = 3000     ## オプティマイザでの反復回数
   ## BFGSを使用してtraining.matrixで自動エンコーダを訓練 
 ##最適化メソッド 
  AE_13 <- autoencode(X.train = train, X.test = val,
                      nl = nl, N.hidden = N.hidden, 
                      unit.type = unit.type,
                      lambda = lambda,
                      beta = beta,
                      rho = rho,
                      epsilon = epsilon,
                      optim.method = "BFGS", #"BFGS", "L-BFGS-B", "CG"
                      max.iterations = max.iterations,
                      rescale.flag = FALSE, 
                      rescaling.offset = 0.001)}, env)
## 訓練及びテストセットの平均二乗誤差を報告する
#cat("autoencode(): mean squared error for training set: ",
#    round(env$AE_13$mean.error.training.set,3),"\n")
## autoencoder.object:から重みWとバイアスbを抽出する
#evalq(P <- AE_13$W, env)
#-----予測-----------
evalq({
  #Train <- predict(AE_13, X.input = train, hidden.output = FALSE) 
  pcTrain <- predict(AE_13, X.input = train, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$train$Class)
  #Val <- predict(AE_13, X.input = val, hidden.output = FALSE) 
  pcVal <- predict(AE_13, X.input = val, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$val$Class)
  #Test <- predict(AE_13, X.input = test, hidden.output = FALSE) 
  pcTest <- predict(AE_13, X.input = test, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$test$Class)
}, env)
#-----グラフ---------------
require(GGally)
evalq({
  ggpairs(pcTrain,columns = 1:ncol(pcTrain), 
          mapping = aes(color = Class),
          title = "pcTrain")}, 
  env)
evalq({
  ggpairs(pcVal,columns = 1:ncol(pcVal), 
          mapping = aes(color = Class),
          title = "pcVal")}, 
  env)
evalq({
  ggpairs(pcTest,columns = 1:ncol(pcTest), 
          mapping = aes(color = Class),
          title = "pcTest")}, 
  env)

チャートをみてみましょう。 

AE_pcTrain

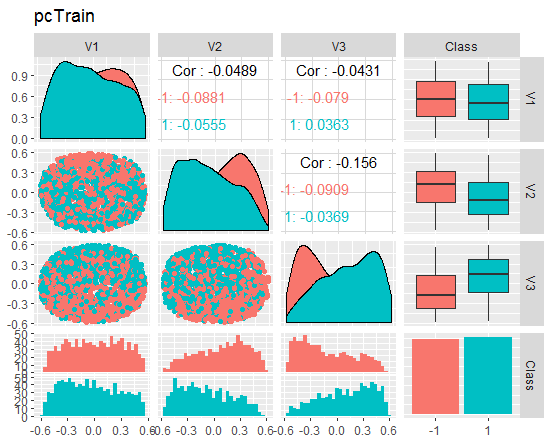
図8　縮小された訓練セットの変動と共分散

 

AE_pcVal

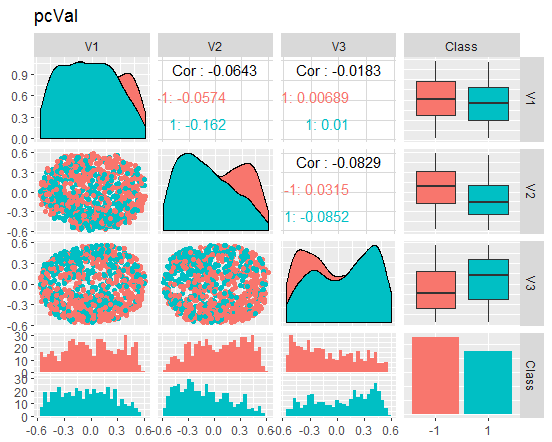
図9　縮小された検証セットの変動と共分散

AE_pcTest

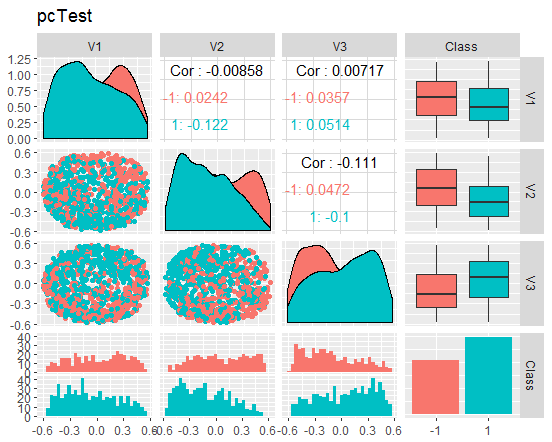
図10縮小されたテストセットの変動と共分散

これらのチャートは何を伝えているのでしょうか？ 主成分（V1、V2、V3）はゴール変数のレベルによってうまく分割されていることがわかります。訓練/テスト/検証セットの分布は歪んでいます。ノイズサンプルを取り除き、これが画像を改善するかどうかを確認する必要があります。ご自分でもできます。

余談：NLPCA

主成分によってデータを分割できるようにするには、純粋な次元削減と、主に 特徴抽出と呼ばれるユニークで有意義な要素の識別と認識に焦点を当てたアプリケーションを区別することが重要です。

ノイズ抑制とデータ圧縮にフォーカスする純粋な次元削減のためのアプリケーションでは、必要なのは記述容量の高い部分空間だけです。個別の成分がこの部分空間を作る方法は限定されていないため、一意である必要はありません。唯一の要件は、部分空間が平均自乗誤差（MSE）に関する最大の情報を提供することです。この部分空間をカバーする別々の成分は、設定された順序や微分された重み付けなしにアルゴリズムによって処理されるため、これは対称訓練タイプと呼ばれます。この種の訓練には、標準的な自己相関ニューラルネットワーク（自動符号化器）によって実行される非線形PCAが含まれ、これはs-NLPCAと呼ばれます。前回の記事では、このバリアントを検討しました。

非線形階層PCA（h-NLPCA）は、成分によってカバーされる最適な非線形部分空間を提供するだけでなく、標準PCAの線形成分と同様に非線形成分を等階層的な順序で制限します。このコンテキストにおける階層は、スケーラビリティと安定性の2つの重要な特性によって説明されます。スケーラビリティは、最初のn個の成分がn次元部分空間によってカバーされ得る最大分散を説明することを意味します。安定性は、n成分の解のi番目の成分がm成分の解のi番目の成分と同一であることを意味します。

階層的な順序は、無相関の成分を生成します。非線形性はまた、h-NLPCAが成分間の複雑な非線形相関を除去できることを意味します。これは有用で有意義な成分をフィルタリングするのに役立ちます。さらに、非線形の無相関成分を単位分散にスケーリングすることにより、複雑な非線形白色化（球面変換）が得られます。これは、回帰、ソースの分類または盲目な分割などのアプリケーションのための、有用な予備処理です。非線形白色化はデータ内の非線形関係を除去するので、さらに使用される方法は線形である可能性があります。これは、この非線形白色化を用いて非線形アプローチに広げることができるICAにとって特に重要です。

階層的な順序にはどのように達することができるのでしょうか。対称的に処理された成分を分散で単純にソートしても、線形にしても非線形にしても、必要な階層序列が生成されません。階層は、2つの相互接続された方法によって実現することができます。すなわち、成分空間における分散を制限するか、元の空間における再構成の誤差の二乗を制限します。線形PCAと同様に、i番目の成分はi番目の分散が最も高いことを考慮する必要があります。

非線形の場合、この制限は、追加の制限なしでは無効または非単位になる可能性があります。逆に、復元誤差は、変換における任意のスケーリングに対して不変の絶対値であるので、より良く制御することができます。したがって、階層的なエラーの制限はより効果的な方法です。単純な線形の場合、成分の階層的な配置はシーケンシャルアプローチによって達成できます。ここで、成分は、前の分散の二乗誤差によって定義される残りの分散から1つずつ抽出されます。非線形の場合、これは、いくつかのネットワークを並行して訓練する間は逐次的にも同時にも実行されません。残りの分散は、非線形変換に関係なく二乗誤差では解釈できません。解決策は、サブネットワークの階層を持つニューラルネットワークを1つだけ使用することです。これにより、エラー関数内ですぐに階層を定式化することができます。

2.5. 逆非線形PCA

本稿のこの部分では、非線形PCAによって逆問題を解決します。元の問題はセット入力から出力を予測することですが、逆問題は設定結果に最もよく一致する入力の評価です。モデルもデータ生成のプロセスもわかっていないので、いわゆる「盲目な」逆問題が発生します。

単純な線形PCAは、必要な成分が出力として予測されるか、対応するアルゴリズムによって入力データとして評価されるかによって、元の問題と逆問題の両方で同等に良好とみなすことができます。自動結合ネットワーク(АЕ)は、直接モデルと逆モデルを同時にモデル化しています。

直接モデルは、抽出関数Fextr：X→ZによってАEの第1部分によって定義されます。逆モデルは、AEの第2部分によって、生成関数Fgen：Z→Xによって定義されます。第1のモデルは線形PCAの場合に適合しており、非線形PCAの場合にはうまく機能しません。これは、このモデルが非常に複雑で、「1対複数」の問題のために解決するのが難しいためです。2つの同一集合Xは、異なるZ成分の値に対応することがあります。

逆非線形РСАは、自動結合ネットワークの第2部分のみを必要とし（図11）、これはネットワーク3-7-12によって例示されます。生成のこの部分は、より小さな次元の画像Zから、Хの大きなサイズのパターンを生成または再構成するFgenの逆反射です。成分Zのこれらの値は、部分層誤差σを入力層Zに伝播すると評価することができる未知の入力です。

逆NLPCA

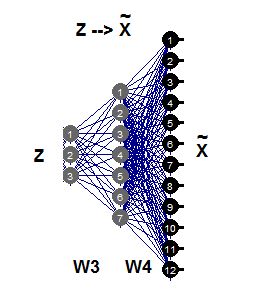
図11　逆非線形РСА

得られた結果をnlpca::pcaMethods関数を使用してAEと比較してみましょう。この関数は、本稿前半で説明しました。同一の初期削減要件12-> 3を有する同じデータの計算を行い、結果を比較します。

そのためには、DTcap.n$trainセットを使用し、目標変数Classを削除し、それを行列に変換します。セットを中心化します。ニューラルネットワークの構造を（3,8,12）とし、残りのパラメータは以下のスクリプトで見つけることができます。結果を取得した後、主成分（スコア）を取り除き、ゴール変数を追加してグラフをプロットします。

このアルゴリズムは非常に低速で、起動ごとに前回とは異なる新しい結果が得られることにご注意ください。

require(pcaMethods)
evalq({
  DTcap.n$train %>% tbl_df %>%
    select(-Class) %>% as.matrix() %>%
    prep(scale = "none", center = TRUE) -> train
  resNLPCA <- pca(train, 
                  method = "nlpca", weightDecay = 0.01,
                  unitsPerLayer = c(3, 8, 12),
                  center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
                  nPcs = 3, completeObs = FALSE, 
                  subset = NULL, cv = "none", # "none""q2"), ...) 
                  maxSteps = 1100)
  rm(train)},
  env)
#--------
evalq(
   pcTrain <- resNLPCA@scores %>% tbl_df %>% 
           cbind(., Class = DTcap.n$train$Class)
, env)
#------グラフ-------
require(GGally)
evalq({
  ggpairs(pcTrain,columns = 1:ncol(pcTrain), 
          mapping = aes(color = Class),
          title = "pcTrain -> NLPCA(3-8-12) wd = 0.01")}, 
  env)
#----------

NLPCA

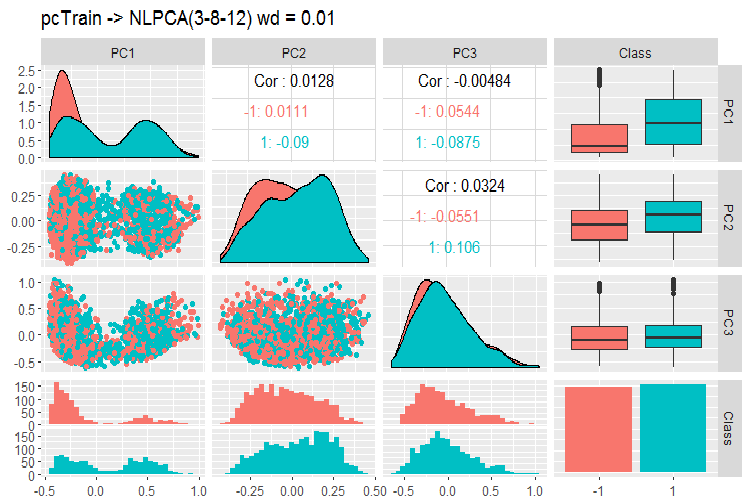
図12　NLPCAを用いた主成分の変動と共分散

チャートから何がわかるでしょうか？主成分はゴール変数のレベルで十分に分けられ、相関は非常に低いです。3番目の成分は不要です。モデルの一般的な情報を見てみましょう。

> print(env$resNLPCA)
nlpca calculated PCA
Importance of component(s):
                 PC1    PC2     PC3
R2            0.3769 0.2718 0.09731
Cumulative R2 0.3769 0.6487 0.74599
12      Variables
2000    Samples
0       NAs ( 0 %)
3       Calculated component(s)
Data was mean centered before running PCA 
Data was NOT scaled before running PCA 
Scores structure:
[1] 2000    3
Loadings structure:
Inverse hierarchical neural network architecture
3 8 12 
Functions in layers
linr tanh linr 
hierarchic layer: 1 
hierarchic coefficients: 1 1 1 0.01 
scaling factor: 0.3260982

ここには問題が1つあります。結果は重み行列W3とW4を返しません。言い換えれば、荷重Pがないので、テストセットと検証セットで主成分S (scores) を得ることができません。この問題は、次元削減の他の2つの適切な方法であるtSNE、ICSでも存在します。これらの問題はまあまあ簡単に解決することができすが、未知の結果をもたらすルートは避けた方が良いでしょう。

パッケージにはさらに確率論的РСАとベイズРСАの2つのメソッドが含まれています。これらは迅速で荷重を返し、検証及びテストセットの主成分を簡単に取得できます。ここではPPCAの例のみを挙げます。

#=======PPCA===================
evalq({
  DTcap.n$train %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> train
  DTcap.n$val %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> val
  DTcap.n$test %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> test
  resPPCA <- pca(train, method = "ppca",
                  center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
                  nPcs = 3, completeObs = FALSE, 
                  subset = NULL, cv = "none", # "none""q2"), ...) 
                  maxIterations = 3000)
  },
  env)
#-----------
>print(env$resPPCA)

ppca calculated PCA
Importance of component(s):
 PC1 PC2 PC3
R2 0.2873 0.2499 0.1881
Cumulative R2 0.2873 0.5372 0.7253
12	Variables
2000	Samples
0 	NAs ( 0 %)
3 	Calculated component(s)
Data was mean centered before running PCA 
Data was NOT scaled before running PCA 
Scores structure:
[1] 2000 3
Loadings structure:
[1] 12 3

Plot a chart for loadings and scores for components 1 and 2:

slplot(env$resPPCA, pcs = c(1,2), 
       lcex = 0.9, sub = "Probabilistic PCA")

ProbPCA

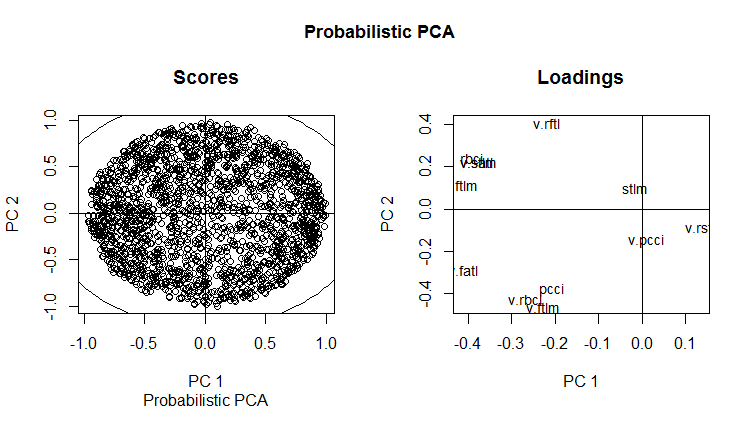
図13　確率的РСАのРС1とРС2（負荷とスコア）

PPCA訓練/テスト/検証セットの主成分の変動と共分散のグラフを以下に示します。スクリプトはGitHubで見つけることができます。

ppcaTrain

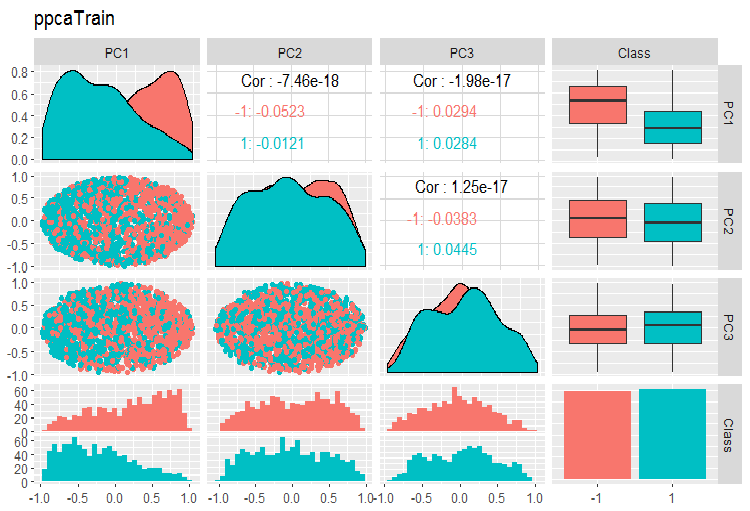
図14　 PPCAで得られた訓練セットの主成分の変動と共分散

ppcaVal

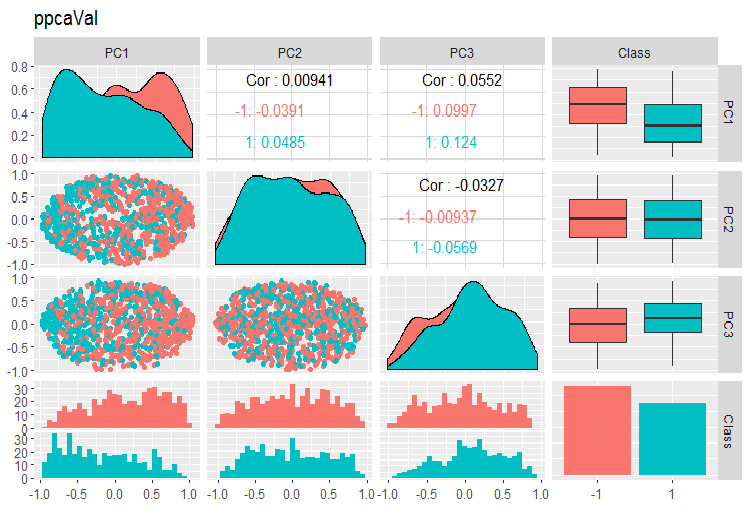
図15　 PPCAで得られた検証セットの主成分の変動と共分散

ppcaTest

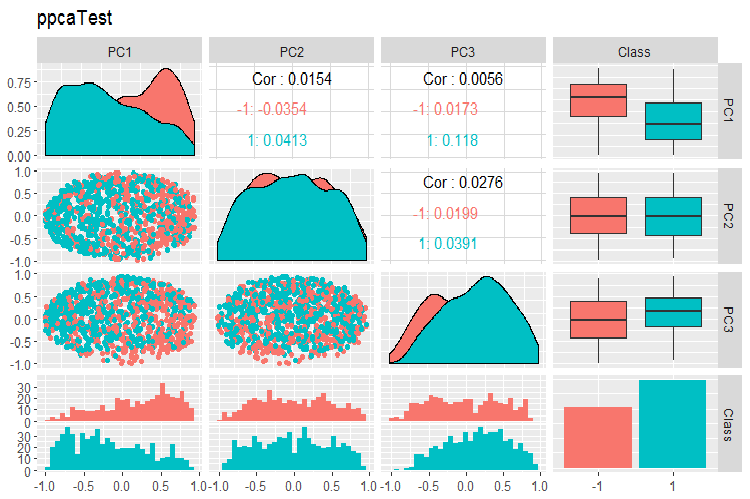
図16　 PPCAで得られたテストセットの主成分の変動と共分散

PPCAで得られた主成分を目標変数のレベルで除算した結果は、以前に考察した自己符号化器を使用した同削減よりも品質的に優れたものではありません。PPCAとBPCAの利点は、スピードとシンプルさです。品質は、特定の分類モデルを使用して評価する必要があります。

データセットの訓練/検証/テストセットへの分割

この部分では、すべてが前の記事で説明したのと同じままです。訓練中：訓練/検証/テスト、スライディングウィンドウ、拡大されるウィンドウ、時にはブートストラップ。モデルの選択中：相互検証。これらのセットの十分なサイズを特定する問題は未だに未解決のままです。

ここで、前処理変換中に訓練セットを使用することに関する Win Wector LLC の興味深い発表に言及したいと思います。彼らは、訓練セットで主成分が特定されていれば、検証データセットで得られた主成分についてモデルを訓練する必要があると述べています。これは、使用済みのセットをモデルの訓練に使用できないことを意味します。 これは、ネットワークが訓練されているときにテストできます。

終わりに

ここでは、ディープニューラルネットワークを訓練するためのデータ準備のほとんどすべての段階を検討しました。ご覧のとおり、これは複雑で時間のかかる段階で、かなりの理論的な知識が必要です。次の段階のデータを準備するための理解とスキルがなければ、それ以上のアクションは意味をなしません。

データを準備する段階ですべての計算を視覚的に制御することなく、良い結果に到達することは不可能です。短気で怠惰な方には、この準備の最適な段階を自動的に見つけるのに役立つ "preprocomb"及び"metaheur"パッケージをお勧めします。

適用

本稿で使用されたスクリプトはGitHub/Part_IIIで入手可能です。


MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/3526

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
クロスプラットフォームEA: ストップ クロスプラットフォームEA: ストップ
この記事では、2つのプラットフォームMetaTrader4とMetaTrader5との互換性を確保するために、EAのストップの実装について説明します。
グラフィカルインターフェイスXI：テーブルセル内のテキストエディットボックスとコンボボックス(ビルド15) グラフィカルインターフェイスXI：テーブルセル内のテキストエディットボックスとコンボボックス(ビルド15)
このライブラリアップデートでは、テーブルコントロール（CTableクラス）に新しいオプションが追加されます。テーブルセル内のコントロールのラインアップが拡張され、今回はテキストエディットボックスとコンボボックスが追加されます。また、このアップデートでは、実行中にMQLアプリケーションのウィンドウのイズを変更する機能も導入されています。
トレードオブジェクト: メタトレーダーのグラフィカルオブジェクトに基づいたトレードの自動化 トレードオブジェクト: メタトレーダーのグラフィカルオブジェクトに基づいたトレードの自動化
この記事では、チャートのリニアマークアップに基づいて自動トレーディングシステムを作成するための簡単なアプローチを扱います。MetaTrader4 およびMetaTrader5のオブジェクトの標準プロパティを使用して既製EAを提供し、トレードオペレーションをサポートしています。
ディープニューラルネットワーク(その2)予測変数の変換と選択 ディープニューラルネットワーク(その2)予測変数の変換と選択
このディープニューラルネットワークシリーズ第2稿では、モデルを訓練するためのデータを準備する過程で予測変数の変換と選択を検討します。