Ticaret için kombinatorik ve olasılık teorisi (Bölüm III): İlk matematiksel model

MetaTrader 5 — Ticaret | 10 Mayıs 2024, 13:28

İçindekiler

Giriş

Bir önceki makalede fraktallar için ilk formülü elde etmiştik. Bu, fraktalla ilgili tüm önemli değerlerin matematiksel bir model kullanılarak tanımlanabileceği varsayımını mümkün kıldı. Simülasyonun bu tür değerleri tanımlaması amaçlanmadı, sadece bu tür yapıların daha derin bir analizini mümkün kılmak için ilk verilerin toplanmasına yardımcı oldu. Bu makalede, farklı Uzman Danışmanlarda uygulanabilecek matematiksel modeli elde edene kadar ilk matematiksel modeli geliştirme sürecinin tamamını açıklamaya odaklanmaya karar verdim.

Yeni fikirler

Bir önceki makalede simetrik bir fraktalı incelerken, aynı simetrik, daha küçük koridorların sayısıyla belirlenen belirli bir koridor içindeki hareketin bir sonucu olarak fiyat tarafından yapılan ortalama adım sayısını hesaplamak için genel bir formül elde ettik. Bu formül aşağıdaki gibidir:

S = K^2 - bir adımın başka bir koridor olduğu gerçeğine dayalı olarak yeni koridorun ortalama adım sayısı
P = K*P0 --> K = P/P0 - bilinen koridorun bilinmeyen koridordan kaç kat daha büyük olduğu
P - ortalama adım sayısı bilinmeyen koridorun genişliği (adımlar orijinal koridorun boyutunun yarısıdır)
P0 - bilinen koridorun genişliği

Asimetrik bir koridoru tanımlayabilmek için, daha önce bahsedilen bazı kavramları daha anlaşılır kılmak amacıyla yeniden tanımlamamız gerekmektedir. Bunlardan en önemlisi K'dir. Bu değer aslında fiyatın yeni koridorda atması gereken adım sayısını yansıtır, ancak adımların sadece yukarı veya sadece aşağı atılması şartıyla. Simetrik bir koridor için, üst veya alt, hangi sınırı dikkate aldığımıza (geçtiğimize) bakılmaksızın adım sayısı eşit olacaktır. Bunun nedeni, problemin hem üst hem de alt sınır için yansıtılmış olmasıdır. Asimetriye gelince, bir önceki makalede kod denemeleri sonucunda, onun durumu için ortalama adım sayısının aşağıdaki gibi belirlendiğini elde ettik:

S = n*m - koridorun asimetrik yarıları için ortalama adım sayısı
n - koridorun üst yarısına sığan basamak sayısı
m - koridorun alt yarısına sığan basamak sayısı

Dolayısıyla, simetrik koridor için "m = n" değerine sahibiz. O zaman, yukarıdakilere dayanarak:

S = n*n = m*m = m*n = n^2 = m^2 = K^2
K = n = m

Bu, ilk türetilen formülün yalnızca bir öncekinin özel bir durumu olduğu ve dolayısıyla K'ya artık ihtiyaç duyulmadığı anlamına gelir.

Bu fonksiyonun ilginç bir özelliği de S(a*k, b*k) = S(a, b)*S(k, k) olmasıdır ki bunu kanıtlamak çok kolaydır:

S(n*k, m*b) = m*k*n*b = n*m*k*b
S(n, m)*S(k, b) = n*m*k*b

Bu özellik çok ilginçtir. Ek yansımalarla, fraktalın tamamını tanımlamak için gerekli tüm formüllerin türetilmesini sağlayabilir. Bu özellik, herhangi bir fraktalın çok önemli bir özelliğini yansıtır: iç içe geçme yeteneği. Başka bir deyişle, büyük karmaşıklığa sahip herhangi bir sonlu fraktal, birbirinin içinde adım görevi gören iki veya daha fazla daha basit fraktal olarak temsil edilebilir. Bu özellik, formülü daha karmaşık durumlar için genelleştirmek amacıyla kullanılacaktır.

Fraktallara geçmeden önce, yukarıda tanımlanan formüllerin yalnızca p = 0.5 ise çalıştığını hatırlatmama izin verin. Piyasa veya fraktal parametreleri rastgele yürüyüşten sapmaya başlar başlamaz, bu formül çok ilginç bir şekilde değişmeye başlar:

Ss[n, m, p] - ortalama adım sayısı için daha genel bir formül (herhangi bir yönde)
S(n, m) = Ss[n, m, 0.5] - rastgele yürüyüş için formül genel formülün özel bir durumudur

Ortalama adım sayısı için genel formül

Daha genel bir formülün şeklini belirlemek için fraktal iç içe geçme ilkesinin değişmezliğini kullandım. Herhangi bir fraktal iç içe geçme seviyesini bir öncekine göre değerlendirirsek, belirli bir adımda hangi adımların gerçekleştiğini düşünmeye gerek yoktur. Böylece, birincil yukarı ve aşağı adımlar, bir önceki seviyenin durumuna karşılık gelen tam olarak aynı sıklık oranlarıyla gerçekleşir. Diğer bir deyişle, ilgili iç içe geçme seviyesinin bir sınırının geçilmesi, bir sonraki iç içe geçme seviyesi için ya bir adım yukarı ya da bir adım aşağıdır. Ancak, mevcut iç içe geçme seviyesi için adımların oluşma sıklığı oranının mevcut seviyenin yapılandırmasına bağlı olmayacağı da bilinmektedir. Bu, fraktal iç içe geçme ilkesinin herhangi bir "p" olasılığı için gözlemlendiği anlamına gelir. Bu, "p" değeri değiştiğinde formülün de değişmesi gerektiği, ancak bir şekilde iç içe geçme özelliğini koruması gerektiği anlamına gelir. Basit bir deney, genel formülün belirlenmesinde bize yardımcı olabilir. p olasılığının bir rastgele yürüyüş noktası ile sıfır ve bir olmak üzere iki uç noktası olduğunu biliyoruz. Fonksiyonun bu üç noktada hangi değerleri alacağını görelim. Aşağıdakileri elde ederiz:

Ss[n, m,1] = Sn[n] = n
Ss[n, m, 0] = Sm[m] = m
Ss[n, m, 0.5] = Sn[n]*Sm[m] = m*n
Sn[n, p] - üst sınıra kadar bir yöndeki adım sayısı
Sn[m, p] - alt sınıra kadar bir yöndeki adım sayısı

İlk durumda aşağıya doğru hiçbir adımımız yoktur - tüm zincirler aynı rotayı izler. İkinci durum ise tam tersidir ve tüm adımlar aşağı doğru olacaktır, yukarı doğru adım olmayacaktır. Uç değerlerde, çarpanlardan biri formülden tamamen kaybolur. Sıfır kuvveti ile bu mümkündür. Sıfır kuvvetine sahip her sayı 1'e eşittir. Buna ek olarak, derece aşağıdaki biçimde bir değişmezliğe sahiptir:

A^X*B^X = (A*B)^X

Sayılar yerine ortalama adımları koyarsak, fraktal iç içe geçme ilkesi yine de korunacaktır. Ayrıca bu, kuvvetin n ve m'ye bağlı olmadığını gösterecektir. Ortalama adım sayısı için elde edilen genel formül aşağıdaki gibidir:

Ss[m, n, p] = (Sn[n]^Pn[p])*(S[m]^Pm[p]) = (n^Pn[p])*(m^Pm[p])

Fraktal iç içe geçme ilkesi şematik olarak şu şekilde gösterilebilir:

Zincirler

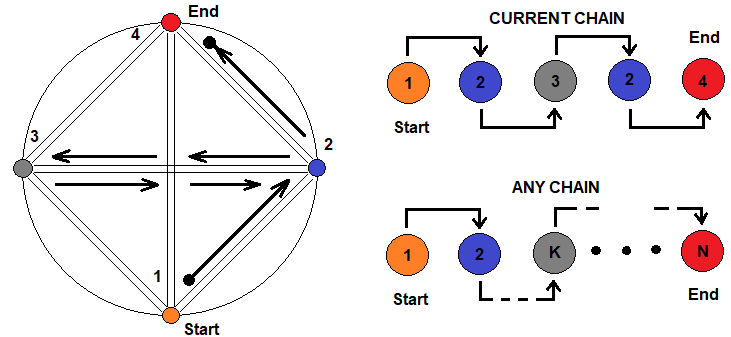
Şekilde, birbirleriyle ifade edilebilen farklı fraktalları sembolize eden dört durum gösterilmektedir. Bir durumdan diğerine geçiş herhangi bir zincir aracılığıyla mümkündür. Rastgele olarak seçilen bir zincir sağda gösterilmektedir. Biraz aşağıda, bu zincirin herhangi bir uzunlukta ve karmaşıklıkta olabileceği ve aynı durumu sınırsız sayıda yineleyebileceğiniz gösterilmektedir. Bu, bir fraktaldaki ortalama adım sayısı formülünün, fraktal iç içe geçme seviyelerini temsil eden bir çarpım zinciri olarak sunulabileceği anlamına gelir.

Bir kuvvet fonksiyonunun prototipini oluşturma

Diğer fikirler fraktal iç içe geçme özelliğinden ve eşit kuvvetteki kuvvet fonksiyonlarının tabana göre değişmezliğinden gelmektedir. Tüm bu matematiksel ilkeler, fraktalların daha derin bir açıklaması için daha fazla formül türetilmesine yardımcı olacaktır. Böylece, ek olarak şeklini bilmediğimiz iki fonksiyon elde ederiz:

Pn[p] - üst sınır çarpanı için kuvvet
Pm[p] - alt sınır çarpanı için kuvvet

Şunları biliyoruz:

Pn[0.5] = 1, Pn[1] = 1, Pn[0] = 0
Pm[0.5] = 1, Pm[1] = 1, Pm[0] = 0

Kuvvet fonksiyonlarını analiz ederek, uygun bir fonksiyon prototipi oluşturmak mümkündür. Aşağıdaki prototipi seçtim:

Pn[p] = 1, if p >= 0.5
Pn[p] = ((1-p)/0.5)^K
Pm[p] = 1, if p <= 0.5
Pm[p] = (p/0.5)^K
K - fonksiyonun düzlüğünü düzenleyen kuvvet

"2" ve "4"ü, belirli bir kuvvetin yumuşak geçişini doğru bir şekilde tanımlayabilen polinomlar şeklinde temsil etmek daha doğru olurdu, ancak bunun burada gereksiz olduğunu düşünüyorum. Eğer daha kesin polinomlar tanımlamak isterseniz, işte prototipler:

Pn[p] = C1*((1-p)/0.5)^K1 + C2*((1-p)/0.5)^K2+ … + CN*((1-p)/0.5)*KN
Pm[p] = C1*(p/0.5)^K1 + C2*(p/0.5)^K2 + … + CN*(p/0.5)^KN
С1+С2+…+…СN = 1 - ilgili kuvvet için ağırlıklardır
KN - karşılık gelen terimin kuvvetidir

Seçtiğim polinom, genel olanın sadece bir terimli en basit versiyonudur. Beyan edilen tüm ilkeler herhangi bir kesirli "n, m" için kontrol edilebilir.

Yukarıdaki varsayımları kontrol etmek için aşağıdaki programı oluşturdum:

Formülün kontrol edilmesi

Program sonuçlarından da görülebileceği gibi, her şey olması gerektiği gibi çalışıyor. Emin olmak için iki sayıyı karşılaştırmanız yeterlidir. Eğer eşitlerse, iç içe geçme ilkesi ve kesirli n ve m kullanma kabiliyeti doğrulanmış olur.

Prototip sınırlı aileden en iyi fonksiyonu elde etmenin genel şeması

Şimdi prototip için gerekli katsayıları nasıl arayacağımızı belirlememiz gerekiyor. En basit arama türünü seçtim - istenen aralıkta rastgele sayılar üretmek. Yöntem şeması aşağıdaki gibidir:

Yaklaşım şeması

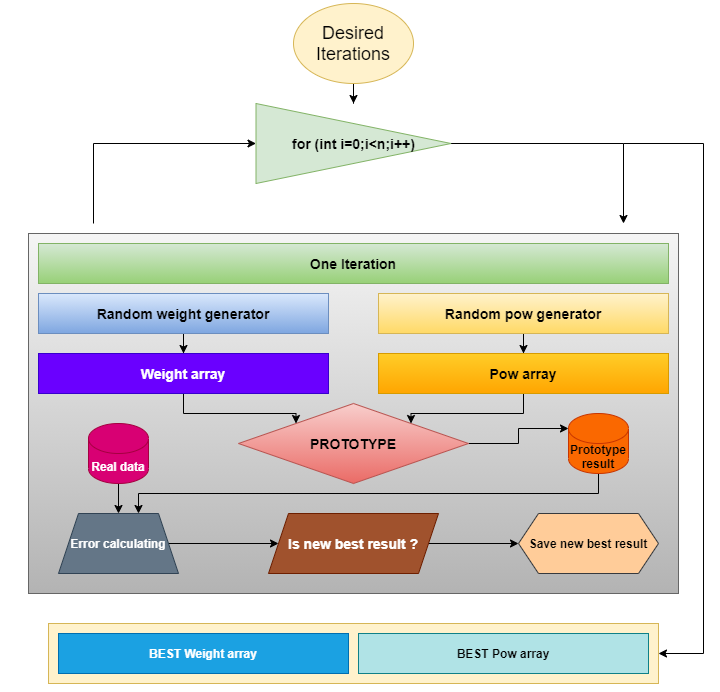
Gerçek verilerin matematiksel modelle en iyi şekilde eşleşmesi için katsayılar bulmamız gerekiyorsa, herhangi bir fonksiyon prototipi için uygundur. Makalenin sonunda aynı yöntemi başka bir prototipi işlemek için uygulayacağımızdan, aynı şema daha sonra da geçerli olacaktır.

Derin analiz

Şimdi bu formülün yapısını daha derinlemesine inceleyelim. Formülün sonucu, fiyatın sınırlardan birini geçmeden önce attığı ortalama adım sayısıdır. Yukarı ve aşağı adımlar eşit kabul edilir, ancak bu eşitlik aslında yalnızca rastgele bir yürüyüş durumunda mümkündür. Asimetrik bir fraktalın tam bir tanımı için, verilen değerin gerçekte nelerden oluştuğunu ayrıca belirlemek gerekir. Mantıksal olarak, herhangi bir adım türünün ortalama sayısı hem üst sınırı geçerkenki ortalama adım sayısına hem de alt sınırı geçerkenki ortalama adım sayısına bağlıdır. Üst sınır geçişi için ilgili değerleri bulalım:

SP[U, ud] = S[U, u]*P[U] + S[U, d]*P[U] = (S[U, u]+S[U, d])*P[U] = S[U]*P[U]
S[U] - adım zincirinin ilk olarak üst sınıra ulaşması koşuluyla herhangi bir adımın ortalama sayısı
S[U, u] - adım zincirinin ilk olarak üst sınıra ulaşması koşuluyla yukarıya doğru olan ortalama adım sayısı
S[U, d] - adım zincirinin ilk olarak üst sınıra ulaşması koşuluyla aşağıya doğru olan ortalama adım sayısı
P[U] - fiyatın ilk olarak üst sınırı geçme olasılığı
SP[U, ud] - üst sınırı geçmek için atılması muhtemel ortalama adım sayısı

Formüller alt sınır için de benzerdir:

SP[D, ud] = S[D, u]*P[D] + S[D, d]*P[D] = (S[D, u]+S[D, d])*P[D] = S[D]*P[D]
S[D] - adım zincirinin ilk olarak alt sınıra ulaşması koşuluyla herhangi bir adımın ortalama sayısı
S[D, u] - adım zincirinin ilk olarak alt sınıra ulaşması koşuluyla yukarıya doğru olan ortalama adım sayısı
S[D, d] - adım zincirinin ilk olarak alt sınıra ulaşması koşuluyla aşağıya doğru olan ortalama adım sayısı
P[D] - fiyatın ilk olarak alt sınırı geçme olasılığı
SP[D, ud] - alt sınırı geçmek için atılması muhtemel ortalama adım sayısı

Açıkça görülüyor ki:

S = SP[U, ud]+SP[D, ud]

Nihayetinde elde edebileceğimiz ve kullanabileceğimiz tüm değerler beş temel değere bağlıdır:

S[U, u] = SP[U, u]/P[U] - adım zincirinin ilk olarak üst sınıra ulaşması koşuluyla ortalama adım sayısı
S[U, d] = SP[U, d]/P[U] - adım zincirinin ilk olarak üst sınıra ulaşması koşuluyla aşağıya doğru olan ortalama adım sayısı
S[D, u] = SP[D, u]/P[D] - adım zincirinin ilk olarak alt sınıra ulaşması koşuluyla yukarıya doğru olan ortalama adım sayısı
S[D, d] = SP[D, d]/P[D] - adım zincirinin ilk olarak alt sınıra ulaşması koşuluyla aşağıya doğru olan ortalama adım sayısı
P[U] - fiyatın ilk olarak üst sınırı geçme olasılığı

Farklı girdi parametreleri ile fraktal sonuçlarına dayanarak bu değerler için formüller arayacağız. Bir önceki makalede fraktal çıktısı için aşağıdaki değerleri seçmiştim:

SP[U, u] - adım zincirinin ilk olarak üst sınıra ulaşması koşuluyla yukarı doğru olan ortalama adım sayısı
SP[U, d] - adım zincirinin ilk olarak üst sınıra ulaşması koşuluyla aşağıya doğru olan ortalama adım sayısı
SP[D, u] - adım zincirinin ilk olarak alt sınıra ulaşması koşuluyla yukarı doğru olan ortalama adım sayısı
SP[D, d] - adım zincirinin ilk olarak alt sınıra ulaşması koşuluyla aşağıya doğru olan ortalama adım sayısı
P[U] - fiyatın ilk olarak üst sınırı geçme olasılığı
P[D] - fiyatın ilk olarak alt sınırı geçme olasılığı
S = SP - herhangi bir adımın ortalama sayısı

Burada temel değerler açısından ifade edilebilecek ayrı bir unsur grubu bulunmaktadır:

SP[U]
S[U, ud] = S[U, u]+S[U, d]
S[D, ud] = S[D, u]+S[D, d]
P[D] = 1-P[U]
S = SP[U, ud]+SP[D, ud]

Fraktalların matematiğiyle uğraşırken, kısaca kompakt bir diyagramda gösterilebilecek kapsamlı analizler yaptım. Diyagram, matematiksel bir model arayışının sonuç sürecini göstermektedir:

Matematiksel bir model için arama sekansı

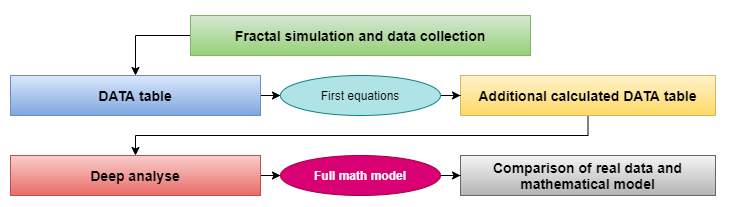
Veri toplama ve sonuçlar

Fraktal hesaplama sonuçlarının daha detaylı incelenmesi sonucunda, evrensel fraktal kavramını oluştururken başlangıçta belirlenen altı değerin matematiksel olarak ilişkili olduğunu fark ettim. Başlangıçta simetrik sınırlar için testler yaptım ve bu değerler arasındaki bağımlılıkları belirlemeye çalıştım. Bazı sonuçlar aldım. Hesaplamaları on farklı durum için yaptım ve yeterli olduğu ortaya çıktı:

Test indeksi	Koridorun üst yarısındaki adımlar (n)	Koridorun alt yarısındaki adımlar (m)	İlk adımın olasılığı (p)	Üst sınır için ortalama olası yukarı adım sayısı (SP[U, u])	Üst sınır için ortalama olası aşağı adım sayısı (SP[U, d])	Alt sınır için ortalama olası yukarı adım sayısı (SP[D, u])	Alt sınır için ortalama olası aşağı adım sayısı (SP[D, d])	Üst sınır için herhangi bir adımın ortalama olası sayısı (SP[U, ud])	Alt sınır için herhangi bir adımın ortalama olası sayısı (SP[D, ud])
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1.25	0.5	0.25	1	1.75	1.25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

Aşağıda fraktal günlüğünde görüntülenmeyen hesaplanmış değerleri içeren bir tablo göstereceğim. Değerler arasındaki bağımlılıkları değerlendirmek için onlara ihtiyacımız olacaktır:

Test indeksi	Koridorun üst yarısındaki adımlar (n)	Koridorun alt yarısındaki adımlar (m)	Üst sınır geçiş olasılığı (P(U))	Alt sınır geçiş olasılığı (P(D))	Üst sınırı geçerken atılan ortalama adım sayısı (S[U, ud]) = SP[U, ud]/P[U]	Alt sınırı geçerken atılan ortalama adım sayısı (S[D, ud]) = SP[D, ud]/P[D]	Üst sınır için ortalama yukarı adım sayısı (S[U, u]) = SP[U, u]/P[U]	Üst sınır için ortalama aşağı adım sayısı (S[U, d]) = SP[U, d]/P[U]	Alt sınır için ortalama yukarı adım sayısı (S[D, u]) = SP[D, u]/P[D]	Alt sınır için ortalama aşağı adım sayısı (S[D, d]) = SP[D, d]/P[D]	Ortalama adım sayısı (S)
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

Bu tablodan, dört bilinmeyen değeri hesaplamak için gereken ilk iki denklemi bulabilirsiniz (diğer tüm değerler bunlardan oluşur). Formülleri elde etmek için S[U, u], S[U, d], S[D, u], S[D, d] sütunlarına dikkat edin. Bu sütundaki sayıların S[U, u], S[U, d] sütunlarında ve S[D, u], S[D, d] sütunlarında çift olarak aynı kesirli kısma sahip olması çok ilginçtir. Ayrıca, S[U, u] > S[U, d] ve S[D, d] > S[D, u] olduğunu görebilirsiniz. Bu değerleri çiftler halinde çıkarır ve m, n ile karşılaştırırsak, bu farkın üst veya alt sınıra karşılık gelen adım sayısına tam olarak eşit olduğu ortaya çıkar:

S[U, u]-S[U, d] = n
S[D, d]-S[D, u] = m

Böylece, temel değerlerin belirlenmesine yardımcı olacak çok önemli iki değer elde ederiz. İki denklem yeterli değildir. Ancak biraz daha farklı bir mantığa dayanarak aynı değerlerin belirlenmesini sağlayacak iki denklem daha elde edebiliriz. Fraktal ile sonsuz uzun bir süre deney yaparsak, yukarı ve aşağı adımların meydana gelme sıklığının oranı, ilgili olasılıklarla orantılı olacaktır.

Bu oranlar şu varsayımla elde edilebilir:

Lim[N0 --> +sonsuz](N0[U]/N0) = p
Lim[N0 --> +sonsuz](N0[D]/N0) = 1-p
Lim[N0 --> +sonsuz](N0[U]/N) = S[UD, u]
Lim[N0 --> +sonsuz](N0[D]/N) = S[UD, d]
Lim[N0 --> +sonsuz](N0/N) = S
N0 - başlangıç adımlarıyla ilişkili olarak gerçekleştirilen temel deneylerin sayısı (karmaşık bir deney oluşturur)
N - basit deneylerden oluşan karmaşık deneylerin sayısı

N0/N0 = 1 çarpanını "3" ve "4"e koyarsak ve içindeki kesirleri uygun şekilde düzenlersek, aşağıdakileri elde ederiz:

Lim[N0 --> +sonsuz](N0[U]/N) = Lim[N0 --> +sonsuz](N0[U]/N0 * N0/N) = Lim[N0 --> +sonsuz](N0[U]/N0) * Lim[N0 --> +sonsuz](N0/N) = p*S = S[UD, u]
Lim[N0 --> +sonsuz](N0[D]/N) = Lim[N0 --> +sonsuz](N0[D]/N0 * N0/N) = Lim[N0 --> +sonsuz](N0[D]/N0) * Lim[N0 --> +sonsuz](N0/N) = (p-1)*S = S[UD, d]

Çarpım limiti, eğer bu limitlerin her biri sonlu bir sayı ise, limitlerin çarpımı olarak gösterilebilir. Limitlerimiz bu koşula uygundur. Bu formüller bu şekilde türetilmiştir. Formüller aşağıdaki gibidir:

S[UD, u] = S*p
S[UD, d] = S*(1-p)

Bu değerleri temel değerler cinsinden ifade etmek daha iyidir - bu, ihtiyacımız olan her şeyi belirlemek için iki eksik denklem sağlar:

S[U, u]*P[U] + S[D, u]*(1-P[U]) = S*p
S[U, d]*P[U] + S[D, d]*(1-P[U]) = S*(1-p)

Sonuç olarak, dört denklemin beş bilinmeyen değeri vardır. Beşinci bilinmeyen, tam grubu oluşturan olasılıklardan biridir (sınırlardan birine ulaşma olasılığı). Beş bilinmeyenin tamamını bulabilmek için beşinci denkleme ihtiyacımız vardır, çünkü bir denklem sisteminin tek bir çözümü olabilmesi için denklem sayısının bilinmeyen sayısına eşit olması gerekir. Beşinci denklem sezgisel olarak elde edilebilir, çünkü bunun yukarı ve aşağı adımlar arasındaki fark olduğunu biliyoruz. İdeal olan, şu limittir:

Lim[Nt[U] --> +sonsuz]((N0[U]-N0[D])/(Nt[U]-Nt[D]) = 1
Nt[U] - temel yukarı adım olasılığı kullanılarak hesaplanan ideal temel yukarı adım sayısı
Nt[D] - temel aşağı adım olasılığı kullanılarak hesaplanan ideal temel aşağı adım sayısı
N0[U] - temel yukarı adımların gerçek sayısı
N0[D] - temel aşağı adımların gerçek sayısı

Sınır geçiş olasılıklarını kullanarak benzer bir limit bulabiliriz:

Lim[Nb[U] --> +sonsuz]((N0[U]-N0[D])/(Nb[U]-Nb[D]) = 1
Nb[U] - üst sınırı geçme olasılığı kullanılarak hesaplanan ideal temel yukarı adım sayısı
Nb[D] - alt sınırı geçme olasılığı kullanılarak hesaplanan ideal temel aşağı adım sayısı
N0[U] - temel yukarı adımların gerçek sayısı
N0[D] - temel aşağı adımların gerçek sayısı

Bu iki limiti kullanarak, bunların toplamı, farkı veya bölümü gibi daha karmaşık bir limit oluşturabiliriz. İfadeyi azaltacak ve N0[U]-N0[D] limitini tamamen ortadan kaldıracak olan bölümü seçeceğim. Bu iki limiti bölerek ve denklemi dönüştürerek şunu elde ederiz:

P[U]*n - (1-P[U])*m = p*S - (1-p)*S

Bu, sınırları geçme olasılıklarını bulabileceğimiz beşinci denklemdir. Sonuç olarak, beş denklemden oluşan bir sistem elde ederiz. Şöyle görünecektir:

S[U, u]-S[U, d] = n
S[D, d]-S[D, u] = m
S[U, u]*P[U] + S[D, u]*(1-P[U]) = S*p
S[U, d]*P[U] + S[D, d]*(1-P[U]) = S*(1-p)
P[U]*n - (1-P[U])*m = p*S - (1-p)*S = 2*p*S - S

Dört bilinmeyenli başlangıç denklem sistemi de aynı sonuç denklemini sağlar. Sistem, değişkenlerin ardışık olarak hariç tutulmasıyla klasik bir şekilde çözülebilir:

--> S[U, u] = n+S[U, d] - “S[U, u]” hariç
--> S[D, d] = m+S[D, u] - “S[D,d]” hariç
(n+S[U, d])*P[U] + S[D, u]*(1-P[U]) = S*p - her şeyi 3. denklemde yerine koyarız
S[U, d]*P[U] + (m+S[D, u])*(1-P[U]) = S*(1-p) - her şeyi 4. denklemde yerine koyarız

Bu dönüşümlerden sonra, sadece 3. denklemi 4’üncüden çıkarmamız gerekir, ardından sezgisel olarak elde ettiğimiz denklemin aynısını elde ederiz. Ne yazık ki, bu denklem sistemi kalan dört değeri bulmamıza izin vermiyor. Bu sistemin işe yarayacağını umuyordum ama yaramadı. Bunun nedenini anlamak için tabloyu fraktal verileriyle analiz etmem gerekti. Bu sayede bu dört büyüklükten biri için bir formül oluşturabildim. Bu ek formül ile geri kalan tüm değerleri bulabiliriz. Böylece, sistemin faydalı olduğu ortaya çıktı.

Tüm matematiksel modelin hesaplanması için algoritma

İlk olarak, S[U, u]'yu bilerek tüm diğerlerini bulmak için ters denklemleri ve bunların kullanım sırasını tanımlayalım. Bu değeri kullanıyorum çünkü hesaplanması için ilgili formülleri bulmayı başardım. Bu değerle, ilk denklemi kullanarak S[U, d]'yi hemen bulabiliriz:

S[U, d] = S[U, u]-n

Ardından, bu iki değeri 3. ve 4. denklemde yerine koyarız ve kalan S[D, u] ve S[D, d] değerlerini buluruz. S[D, u] üçüncü denklemden hemen hesaplanabilir:

S[D, u] = (S*p - S[U, u]*P[U])/(1-P[U])

Şimdi, sadece son bilinmeyen değer için bir formül bulmamız gerekiyor. S[U, d] için elde edilen ifadeyi dördüncü denklemde yerine koyalım:

S[D, d] = (S*(1-p) - S[U, d]*P[U])/(1-P[U]) = (S*(1-p) - (S[U,u]-n)*P[U])/(1-P[U])

Eksik olan tek unsur, beşinci denklemin çözülmesiyle kolayca elde edilebilecek olan P[U] değeridir. Şimdi bunu yapalım.

P[U]*n - (1-P[U])*m = 2*p*S-S
--> P[U]*(n+m) = 2*p*S-S+m
--> P[U] = (2*p*S-S+m)/(n+m)

Burada bilinen değerler şunlardır:

n - üst sınıra kadar olan adım sayısı
m - alt sınıra kadar olan adım sayısı
p - ilk yukarı adım olasılığı
S[U, u] - üst sınırın geçilmesi koşuluyla ortalama yukarı adım sayısı
P[U] - üst sınırı geçme olasılığı

4. değer hesaplanabilir:

S[U, u] = Ss[m, n, p] = (n^Pn[p])*(m^Pm[p])
Pn[p] = 1, if p >= 0.5
Pn[p] = ((1-p)/0.5)^K
Pm[p] = 1, if p <= 0.5
Pm[p] = (p/0.5)^K
K - fonksiyonun düzlüğünü düzenleyen kuvvet

Düzlük katsayısını biraz sonra ayrı bir programda hesaplayacağız. Şimdi en önemli değeri belirlememiz gerekiyor. Tablodaki S[U, u] değerini analiz ederek, simetrik sınırlar için iki değerin formüllerini türetmeyi başardım:

S[U, u] = Summ[i = 0, n](i); if n == m
S[U, d] = Summ[i = 0, n](i-1); if n == m

Sorun, bu formüllerin yalnızca p = 0.5 ve simetrik sınırlar için çalışmasıdır. Formül kavramı asimetrik sınırları da kapsayacak şekilde genişletilmelidir. Devamında, bunu farklı p değerleri için genelleştirebiliriz. Genellemeye geçmeden önce, tablodaki test sonuçlarının sadece "m > n" için geçerli olduğuna dikkat edin. Eğer "m < n" ise, formüller "S[D, d], S[D, u]" için çalışacaktır. Bu durumda, diğer tüm bilinmeyen değerleri bulmak için algoritmanın bir ayna benzerini oluşturmak gerekir.

Benzer şekilde, S[D, d] durumu için ters denklemleri ve hangi sırada kullanılmaları gerektiğini tanımlayalım. Yine, ikinci denklemi kullanarak S[D, u] değerini buluyoruz:

S[D, u] = S[D, d]-m

Sonrasında her iki değer de S[U, u] ve S[U, d]'yi bulmak için 3. ve 4. denklemde yerine konulabilir. S[U, d] dördüncü denklemden hemen hesaplanabilir:

S[U, d] = (S*(1-p) - S[D, d]*(1-P[U]))/P[U]

Şimdi, sadece son bilinmeyen değer için bir formül bulmamız gerekiyor. S[U,d] için elde edilen ifadeyi üçüncü denklemde yerine koyalım:

S[U, u] = (S*p - (S[D, d]-m)*(1-P[U]))/P[U]

Sonuç olarak, S[U, u], S[D, d] formüllerini "n! = m" durumları için genelleştirmek üzere gerekli tüm verileri elde ettik. Tablo verilerinin analizinden aşağıdaki veriler elde edildi:

m > n, p = 0.5
S[U, u] = Summ[i = 0…n](i)+(m-1)/3

Tersi durum için:

m < n, p = 0.5
S[D, d] = Summ[i = 0…m](i)+(n-1)/3

Simetrik sınırlara sahip standart durum için hesaplamalar daha basit olacaktır:

m = n, p = 0.5
S[U, u] = Summ[i = 0…n](i)
S[D, d] = Summ[i = 0…m](i)

Son denklemi elde etmek için prototipler

Şimdi tüm olası p değerleri için S[U, u], S[D, d]'yi tanımlayacak değiştirilmiş fonksiyonun bir prototipini tanımlayalım. Temel bir çalışan prototip oluşturmak için p ekseninde üç noktaya ve genel yapıya ilişkin birkaç varsayıma ihtiyacımız var. İki tür genel fonksiyonu ele almanın yeterli olduğuna inanıyorum:

Sp[U, u] = S[U, u]^K(p)
Sp[D, d] = S[D, d]^K(q)
q = 1-p

İlk tür, gerçek bir çalışan prototip veya yapının farklı olduğunu ve başka bir mantık gerektirdiğini gösteren belirli bir işaret olabilir. Kuvvet fonksiyonunun tüm verileri bir araya getirebildiği ortaya çıktı. Elbette daha karmaşık, belki daha doğru prototipler olabilir, ancak bizim çözümümüzün oldukça yeterli olduğunu düşünüyorum. En önemli şey mantığı anlamaktır. Bununla birlikte, modele ince ayar yapmak isterseniz, makalede sunulan verilere dayanarak bunu yapabileceksiniz. Bir test programı oluşturdum:

Prototiplere dayalı bulunan fonksiyonlar

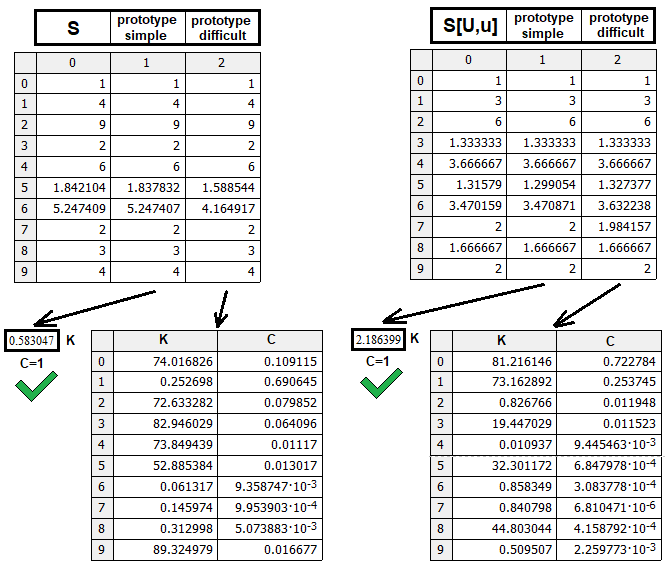
Program S(n, m, p) ve S[U, u](n, m, p) prototiplerinin her ikisini de kontrol eder. S[D, d](n, m, p) için kontrol gerekmez, çünkü bu fonksiyon S[U, u](n, m, p)'ye yansıtılır ve böylece S[D, d](n, m, p) = S[U, u](m, n, p-1) olur. Şekil, bulunan prototiplerin verimlilikleri açısından karşılaştırılmasını göstermektedir. Her prototip, formüllerdeki ağırlıkların ve kuvvet katsayılarının aynı sayıda rastgele kombinasyonuyla test edilmiştir. Daha basit prototip, aynı sayıda arama döngüsü ile daha güzel sonuçlar göstermektedir. Gerekirse, daha karmaşık prototiplerin neler yapabileceğini görmek için ek hesaplamalar yapmak mümkündür.

Kontrol ettikten sonra, iç içe geçmiş "K(p)", "K(q)" fonksiyonlarının iç yapısını tanımlamamız gerekir. İç yapısı p = 0, p = 0.5, p = 1, q = 0, q = 0.5, q = 1 noktalarında zorunlu çakışmayı sağlamalıdır. Bu noktalardaki fonksiyon değerlerini biliyoruz, bu da gerekli prototipin daha kolay seçilmesini sağlıyor:

p = 0.5; Sp[U, u] = S[U, u] --> K(0.5) = 1
p = 1.0; Sp[U, u] = n = S[U, u]^(Log[S[U, u] --> n]) --> K(1.0) = Log[S[U, u] --> n]
p = 0.0; Sp[U, u] = 0 = S[U, u]^(-sonsuz) --> K(0.0) = -sonsuz
q = 0.5; Sp[D, d] = S[D, d] --> K(0.5) = 1
q = 1.0; Sp[D, d] = n = S[D, d]^(Log[S[U, u] --> m]) --> K(1.0) = Log[S[D, d] --> m]
q = 0.0; Sp[D, d] = 0 = S[D, d]^(-sonsuz) --> K(0.0) = -sonsuz

Birinci ve dördüncü ifadeler, rastgele yürüyüş noktasında kuvvetin bire eşit olması gerektiğini göstermektedir. İkinci ve beşinci ifadeler, kuvvetin öyle olması gerektiğini gösterir ki, bir değer ona yükseltildiğinde, yukarıdaki sonuç tablosunda görülebileceği gibi ya "n" ya da "m" elde ederiz. Üçüncü ve altıncı ifadeler, sıfır oluşması için kuvvetin eksi sonsuza yönelmesi gerektiğini göstermektedir. Bu gerçek ayrıca p ve q değerlerinin prototipin paydasında olması gerektiğini belirtir, çünkü sıfıra bölme işlemi sonsuzluk gibi değerlere yol açar. Bir fonksiyon için kuvvet yasası prototipi oluşturma deneyimimiz zaten vardı. Bunu bir temel olarak kullanabilir ve revize edebiliriz. Görevi derinlemesine analiz ettikten sonra şu prototipe ulaştım:

K(p) = 1 + D*Summ(N)(Kn[0]*|((p-0.5)/(0.5*p))|^A[0] + Kn[1]*|((p-0.5)/(0.5*p))|^A[1] + …. + Kn[N]*|((p-0.5)/(0.5*p))|^A[N])
Kn[0]+Kn[1]+… +Kn[N] = Log[S[U, u] --> n]-1
D = ((p-0.5)/(0.5*p)) / |((p-0.5)/(0.5*p))|
K(q) = 1 + C*Summ(N)(Km[0]*((q-0.5)/(0.5*q))^B[0] + Km[1]*((q-0.5)/(0.5*q))^B[1] + …. + Km[N]*((q-0.5)/(0.5*q))^B[N])
Km[0]+Km[1]+… +Km[N] = Log[S[D, d] --> m]-1
C = ((q-0.5)/(0.5*q)) / |((q-0.5)/(0.5*q))|
Kn, Km - uygun terimlerin ağırlıkları
A, B - terimlerin hassasiyeti

Fonksiyon karmaşık görünse de basit bir mantığa dayanmaktadır. "p = 0.5, q = 0.5" ise, toplam işaretinin altındaki her şey sıfıra döner ve sadece 1 kalır, böylece "1", "4" koşulları sağlanır. "p = 1, q = 1" ise, bir kuvvete yükseltilen toplam içindeki ilgili kesirler 1'e dönüşür: |((p-0.5)/(0.5*p))|. Bu terimler, bir kuvvete yükseltilirken fonksiyonun karmaşık değerlerini hariç tutmak için mutlak işaretiyle yazılır. Bunun yerine, ilgili işaret ek bir çarpan olarak sağlanır. Kuvvet artık bu terimleri etkilemez ve tüm toplam Log[S[U, u] --> n]-1, Log[S[D, D] --> m]-1'e dönüşür. Bu sayıyı 1'e ekleyerek fonksiyonun gerekli değerlerini elde ederiz: Log[S[U, u] --> n], Log[S[D, d] --> m].

İnterpolasyon polinomları da benzer bir mantığa göre oluşturulur, bunun bir örneği de iyi bilinen Lagrange polinomudur. Polinomumuz, uygulanabileceği belirli bir görev için tasarlanmıştır. Avantajı, göreve tam uyum sağlamasıdır. Bu eğri ailesinden istenen fonksiyonu bulmak için sadece iki sayı dizisi bulmamız gerekir.

Matematiksel modelin uygulaması ve testi

Bulunan ifadelerle, herhangi bir fraktalın hesaplanması için gerekli işlevselliği kolayca uygulayabiliriz. Ana fonksiyonun geri döndüreceği tüm veriler için bir depo olacak tek bir yapıya ihtiyacımız olacaktır. Diğer fonksiyonlar yardımcı olacaktır. Sadece son fonksiyona ihtiyacımız var:

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

Matematiksel modeli kontrol etmek için bu kodun bir benzerini MathCad15'te uyguladım. Matematiksel model doğru bir şekilde oluşturulmuşsa, tablodan elde edilen sonuçlar matematiksel model tarafından geri döndürülen sonuçlarla örtüşmelidir. Program dökümü makaleye eklenmiştir, böylece kendiniz kontrol edebilirsiniz. Makalede çok fazla yer kaplayacağı için dökümü doğrudan makaleye eklememeye karar verdim, ancak sonucu mutlaka görmelisiniz. Matrisleri karşılaştıralım ve matematiksel modelin uygulanabilir olduğundan emin olalım:

Matematiksel modelin doğruluğunun kontrol edilmesi

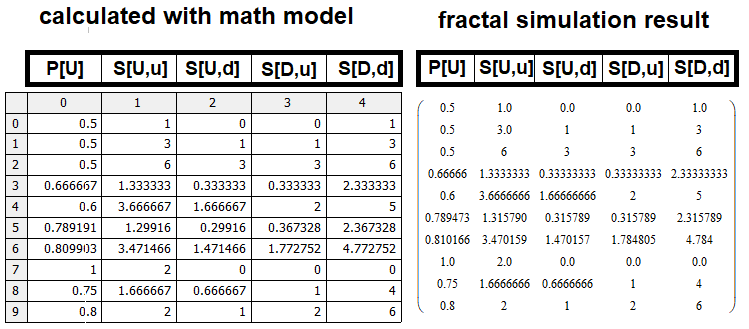
Elbette, S, S[U, u], S[D, d] değerleri için bulduğumuz prototiplerin verimliliğinden kaynaklanan bazı yanlışlıklar var. Küçük farklılıklar için ek bir faktör, simülasyon yanlışlıklarıyla ilgili olabilir; bu yanlışlıklar, simüle edilen n ve m'nin daha büyük değerleri için daha büyüktür, çünkü sınırlı hesaplama gücü nedeniyle simülasyon derinliğini sınırlamak zorundayız.

Sonuç

Bu matematiksel modeli geliştirmek için çok zaman harcadım, çünkü tüm matematiği sıfırdan oluşturmak zorundaydım. Ancak, sonuçtan memnunum. Sonraki makalelerde, bir araya getirildiklerinde herhangi bir ticaret konfigürasyonunun temel özellikleri açısından hesaplanmasına olanak tanıyacak daha evrensel matematiksel modeller geliştirmeye çalışacağım. Ayrıca, matematiksel model yalnızca fiyatlandırma süreçlerini tanımlamak için değil, aynı zamanda ticaret sinyallerini tanımlamak ve karmaşık stratejileri basitleştirerek daha basit olanlara indirgemek için de kullanılabilir. Bu biraz zaman alacaktır.

Referanslar

Ticaret için kombinatorik ve olasılık teorisi (Bölüm I): Temel bilgiler

Ticaret için kombinatorik ve olasılık teorisi (Bölüm II): Evrensel fraktal

MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/9570

Ekli dosyalar |

ZIP indir

Materials.zip (312.85 KB)

Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.

Bu yazarın diğer makaleleri

Tartışmaya git

MQL4 ve MQL5 geliştirme çerçevesinde OpenAI'ın ChatGPT özellikleri

Bu makalede, Uzman Danışmanlar, göstergeler ve komut dosyaları geliştirmenin zaman ve emek yoğunluğunu azaltma açısından yeteneklerini anlamak için OpenAI'dan ChatGPT ile uğraşacağız. Size bu teknolojide hızlı bir şekilde yol göstereceğim ve MQL4 ve MQL5'te programlama için doğru şekilde nasıl kullanılacağını göstermeye çalışacağım.

Ticaret için kombinatorik ve olasılık teorisi (Bölüm II): Evrensel fraktal

Bu makalede fraktalları incelemeye devam edeceğiz ve tüm materyali özetlemeye özellikle dikkat edeceğiz. Bunu yapmak için, daha önceki tüm gelişmeleri, ticarette pratik uygulama için uygun ve anlaşılabilir olacak kompakt bir forma getirmeye çalışacağım.

İşte Karışınızda Yeni MetaTrader 5 ve MQL5

Bu MetaTrader 5 ile ilgili sadece kısa bir inceleme. Sistemin tüm yeni özelliklerini bu kadar kısa sürede açıklayamam, test süreci 09.09.2009’da başladı. Bu sembolik bir tarihtir ve şanslı sayı olacağına eminim. MetaTrader 5 terminalinin ve MQL5’in beta sürümünü beş gün önce aldım. Tüm özelliklerini deneme şansım olmadı ama şimdiden etkilendim.

Ticaret için kombinatorik ve olasılık teorisi (Bölüm I): Temel bilgiler

Bu makale serisinde, ticaret ve fiyatlandırma süreçlerini tanımlamak için olasılık teorisinin pratik bir uygulamasını bulmaya çalışacağız. İlk makalede, kombinatorik ve olasılığın temellerine bakacağız ve fraktalların olasılık teorisi çerçevesinde nasıl uygulanacağına dair ilk örneği analiz edeceğiz.