您应该知道的 MQL5 向导技术（第 05 部分）：马尔可夫（Markov）链

MetaTrader 5 — 测试者 | 15 五月 2023, 09:03

1 007

Stephen Njuki

概述

马尔可夫（Markov）链是一个强大的数学工具，能够针对包括金融在内的各个领域的时间序列数据进行建模和预测。在金融时间序列建模和预测中，马尔可夫链通常用于模拟金融资产随时间的演变，例如股票价格或汇率。马尔可夫链模型的主要优点之一是其简单性和易用性。它们基于一个简单的概率模型，该模型描述了系统随时间推移的演变，并且不需要复杂的数学假设、或关于数据统计属性的假设。这令其对于建模和预测金融时间序列数据特别实用，这些数据可能非常复杂，并表现出非平稳行为。

马尔可夫链模型的建模可分为四种主要类型：离散时间马尔可夫链、连续时间马尔可夫链、隐性马尔可夫模型、和切换马尔可夫模型。其中主要的是：离散时间马尔可夫链，用于模拟系统在一系列离散时间步长的演变；连续时间马尔可夫链，用于模拟系统在连续时间间隔内的演变。这两者都可针对金融时间序列数据进行建模和预测。

针对金融时间序列数据的马尔可夫链模型进行概率估算可经由多种途径完成。我要指出 8 个，其中最突出的是期望最大化。这是 alglib 采用我的 MQL5 代码库实现的方法。

一旦估算出概率（或马尔可夫链模型的参数），该模型就可用于预测未来的状态或事件。例如，在金融时间序列数据的情况下，马尔可夫链模型可用于根据市场当前状态和不同市场状态之间的转移概率预测未来的股票价格或汇率。

链建模

马尔可夫链是一个数学系统，它遵循某些概率规则从一种状态过渡到另一种状态。马尔可夫链的定义特征是，无论系统如何到达其当前状态，过渡到任何特定状态的概率仅取决于当前状态和经历的时间。马尔可夫链可以使用状态图表示，其中图中的每个节点表示一个状态，节点之间的连线表示状态之间的转换。从一种状态过渡到另一种状态的概率由相应连线的权重表示。

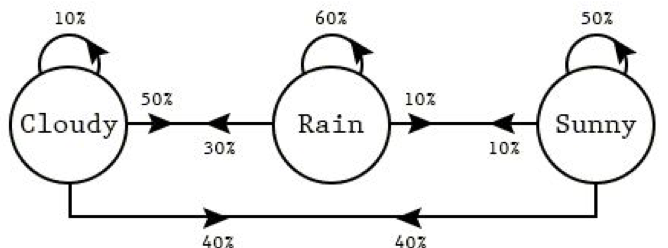
图中的箭头（又名马尔可夫链）表示状态之间的转换。从状态“雨天”过渡到状态“晴天”的概率可以用两个节点之间的连线权重（在本例中为 0.1）表示，对于其它转换也是如此。

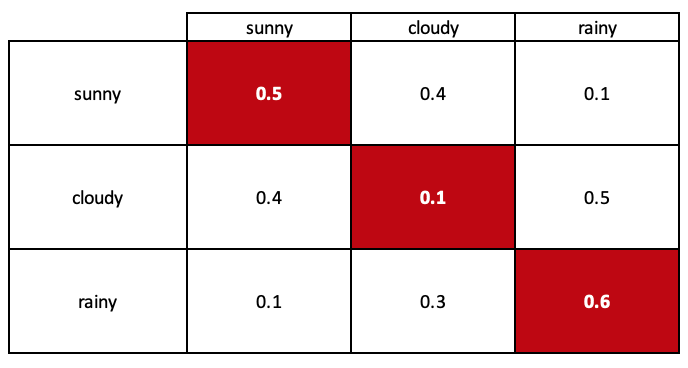
我们可以使用此状态图来模拟系统中状态之间转换的概率。我们创建的模型最好称为过渡矩阵，如上所示。

马尔可夫链的一个重要假设是，系统的未来行为仅取决于当前状态和所经历的时间，而不取决于系统流逝的历史。已知这被称为马尔可夫链的“无记忆”属性。这意味着从一种状态过渡到另一种状态的概率是相同的，无论系统可能经过多少中间状态才能达到其当前状态。

马尔可夫链可针对各种系统进行建模，包括金融系统、天气系统和生物系统。它们对于那些表现出时态依赖性的系统进行建模特别有用，其中系统的当前状态取决于其过去的状态，例如时间序列。

马尔可夫链广泛用于针对时间序列数据进行建模，时间序列数据是随时间定期收集的一序列数据点。时间序列数据可以在许多不同的领域发现，例如金融、经济学、气象学和生物学。

为了利用马尔可夫链针对时间序列数据进行建模，首先需要定义系统的状态，以及它们之间的转换。状态之间的转移概率可采用最大似然、或期望最大化、等技术从数据里估算。一旦估算出转移概率，马尔可夫链就可以用来根据当前状态和经历的时间预测未来的状态或事件。

马尔可夫链可以通过若干种方式针对时间序列数据进行建模：

离散时间马尔可夫链：离散时间马尔可夫链是一种数学模型，用于描述涵盖一序列时间步骤的离散时间内随机过程的演变。它可用于对一序列事件或状态进行建模，其中在给定时间转换到任何给定状态的概率仅取决于当前状态。

此处是如何使用离散时间马尔可夫链对日常事件进行建模的一些示例：

天气预报：离散时间马尔可夫链可针对特定地点的日常天气进行建模。马尔可夫链的状态可以代表不同的天气条件，例如晴天、多云、下雨或下雪。转移概率可以从历史天气数据中推测出来，马尔可夫链可用来根据当前的天气状况对第二天的天气进行预报。
股价走势：离散时间马尔可夫链可用于模拟特定股票价格的每日走势。马尔可夫链的状态可以代表不同水平的价格变动，例如上涨、下跌或不变。转移概率可以依据历史股价数据推算出来，马尔可夫链可以用来根据当前的价格走势对第二天的股价走势进行预测。
交通模板：离散时间马尔可夫链可用于对特定道路或高速公路上的日常交通模板进行建模。马尔可夫链的状态可以代表不同程度的交通拥堵，例如轻度、中度或重度。转移概率可以依据历史交通数据中推算出来，马尔可夫链可根据当前的交通拥堵水平预测第二天的交通拥堵程度。

连续时间马尔可夫链：这里状态之间的转换是连续发生的，而不是在离散的时间步骤内发生的。这意味着从一种状态转换到另一种状态的概率取决于自上次转换以来经历的时间。连续时间马尔可夫链通常用于模拟在不同时间跨度内连续变化的系统，例如特定高速公路上的交通流量、或化工厂中的化学反应速率。离散时间和连续时间马尔可夫链之间的主要区别之一是，连续时间马尔可夫链中的转移概率以转移速率为特征，即每单位时间从一个状态过渡到另一个状态的概率。这些转换速率用于计算在特定时间间隔内从一个状态转换到另一个状态的概率。
隐性马尔可夫模型：隐性马尔可夫模型（HMM）是一种马尔可夫链统计模型，其中系统的状态不能直接观察到，而是从一系列观察中推断出来。以下是如何使用隐性马尔可夫模型对常见日常事件进行建模的一些示例：
- 语音识别：隐性马尔可夫模型可用于模拟语音过程中产生的声音，并识别口语。在这种情况下，HMM 的状态可以表示不同的音素（语音），并且观察可以是表示口语的声波序列。 HMM 可以基于口语单词及其相应声波的大型数据集合上进行训练，并且可以通过根据观察到的声波推断最可能的音素序列，来识别新的口语单词。
- 手写识别：隐性马尔可夫模型可用于模拟手写过程中笔划的顺序，并识别手写单词。在这种情况下，HMM 的状态可以代表不同的笔划，并且观察结果可以是手写单词的图像序列。 HMM 可以基于手写单词及其相应图像的大型数据集上进行训练，并且可以通过根据观察到的图像推断最可能的笔划序列，来识别新的手写单词。
- 活动识别：隐性马尔可夫模型可用于根据一系列观察结果（例如传感器读数或视频帧）识别人类活动。例如，HMM 可用于识别行走、跑步或跳跃等活动。
马尔可夫切换模型：马尔可夫切换模型（MSM）是一种马尔可夫链，其中系统的状态可以根据某些条件随时间变化或“切换”。以下是如何应用马尔可夫切换模型对常见的日常事件进行建模的一些示例：
- 消费者行为：马尔可夫转换模型可针对消费者的购买行为进行建模。 MSM 的状态可以表示不同类型的购买行为，例如高频购买、或低频购买。各状态之间的过渡可能基于某些条件，例如收入变化、或新产品的引入。 MSM 可根据当前状态和状态之间的转换概率预测未来的购买行为。
- 经济指标：马尔可夫转换模型可针对经济指标进行建模，例如 GDP 或失业率。 MSM 的状态可能代表不同的经济状况，例如通胀或通缩，并且状态之间的过渡可以基于某些条件，例如货币政策、或商业周期的变化。 MSM 可根据当前状态和状态之间的转移概率预测未来的经济状况。
- 交通模板：马尔可夫切换模型可针对特定道路或高速公路上的交通模板进行建模。 MSM 的状态可以表示不同级别的流量拥堵，例如轻度、中度或重度，状态之间的转换可以基于某些条件，例如一天中的时间或星期几。 MSM 可根据当前状态和状态之间的转换概率预测未来的流量模板。

与任何假设一样，总是存在潜在的假设，倾向于对想法施加某种形式的限制。马尔可夫链也不例外，以下是一些假设：

平稳性：马尔可夫链的主要假设之一是状态之间的转移概率随时间变化是恒定的。这种假设称为平稳性。如果转移概率随时间变化并不恒定，则马尔可夫链模型可能不准确。
马尔可夫性质：马尔可夫链的另一个假设是，系统的未来演化仅取决于当前状态和经历的时间，并且不受超出系统当前状态的以往历史的影响。这种假设在实践中也许并非始终成立，特别是对于具有复杂依赖关系、或长期记忆的数据集。
有限状态空间：马尔可夫链通常在有限状态空间上定义，这意味着系统可以处于有限数量的可能状态。这可能不适用于具有大量状态或连续变量的数据集。
时间同质性：马尔可夫链通常被认为是时间同质性，这意味着状态之间的转移概率不依赖于转变发生的特定时间。如果转移概率的确取决于转移发生的时间，则马尔可夫链模型可能不准确。
遍历性：马尔可夫链通常被认为是遍历性的，这意味着在有限的步骤内从任何其它状态有可能到达任何状态。如果不满足此假设，马尔可夫链模型可能不准确。

通常，马尔可夫链模型最适合具有相对简单依赖关系，和少量状态或变量的数据集。如果数据集具有复杂的依赖关系，或大量的状态或变量，则其它建模技术可能更合适。

概率估算

一旦马尔可夫链被建模，我们就需要估算从每个状态转换的概率。这里有许多可用方法，最有帮助的就是迭代它们来更好地了解马尔可夫链的范围和可能性。有若干种方法可以估算马尔可夫链中状态之间转换的概率，包括：

最大似然估算（MLE）：在最大似然概率估算（MLE）中，目标是根据观测数据估算事件或事件序列的概率。在马尔可夫链的关联环境中，这意味着我们希望根据一组观察到的转换来估算从一种状态过渡到另一种状态的概率。
为了实现马尔可夫链的 MLE，我们首先需要收集一组观察到的转换。这可以通过运行模拟或收集真实世界的数据来完成。一旦我们有了观察到的转变，我们就可以应用它们来估算转变概率。

为了估算转移概率，我们可以采取以下步骤：
- 定义一个矩阵来存储转移概率。矩阵的维数应该是 num_states x num_states，其中 num_states 是马尔可夫链中的状态数量。
- 初始化矩阵，所有概率设置为 0。这可以利用迭代矩阵所有元素的嵌套循环来完成。
- 迭代观察到的转换，并更新转换概率。对于从状态 i 到状态 j 每个观察到的转换，将概率 transition_probs[i][j] 加 1。
- 对转移概率进行归一化，使其总和为 1。这可通过将矩阵中的每个元素除以相应行中元素的总和来完成。
一旦转移概率估算完毕，我们就可以利用它们来预测从一种状态过渡到另一种状态的可能性。例如，如果我们想预测从状态 i 过渡到状态 j 的概率，我们可以使用公式 P(j | i) = transition_probs[i][j]。
.
贝叶斯（Bayesian）估算：该方法涉及采用贝叶斯定理，根据新数据更新模型参数上的概率分布。为了将贝叶斯概率估算与马尔可夫链一起使用，我们首先需要定义马尔可夫链状态的先验分布。这种先验分布代表了我们对链中不同状态的概率的最初可信度。然后，当新信息可用时，我们可以利用贝叶斯来更新我们对状态概率的可信度。例如，假设我们有一个含有三种状态的马尔可夫链：A、B 和 C。我们从各状态的先验分布开始，这可能表示为：
P(A) = 0.4 P(B) = 0.3 P(C) = 0.3

这意味着，最初，我们认为处于状态 A 的概率是 40%，处于状态 B 的概率是 30%，处于状态 C 的概率是 30%。

现在假设我们观察到系统从状态 A 转换到状态 B。我们可以基于这些新信息，利用贝叶斯概率估算来更新我们对状态概率的可信度。为此，我们需要知道状态之间的转移概率。我们假设转移概率如下：

P(A -> B) = 0.8

P(A -> C) = 0.2

P(B -> A) = 0.1

P(B -> B) = 0.7

P(B -> C) = 0.2

P(C -> A) = 0.2

P(C -> B) = 0.3

P(C -> C) = 0.5

这些转换概率告诉我们从一种状态过渡到另一种状态的概率。例如，从状态 A 转换到状态 B 的概率为 0.8，而从状态 A 转换到状态 C 的概率为 0.2。

使用这些转移概率，我们现在可以利用贝叶斯概率估算来更新我们对状态概率的可信度。特别是，我们可以依据给定系统从状态 A 过渡到状态 B 的新信息，利用贝叶斯规则来计算状态的后验分布。这种后验分布代表了我们对状态概率的最新可信度，其参考了我们收到的新信息。

例如，使用贝叶斯规则，我们可以计算处于状态 A 的后验概率，如下所示：

P(A | A -> B) = P(A -> B | A) * P(A) / P(A -> B)

代入先验分布和转移概率的值，我们得到：

P(A | A -> B) = (0.8 * 0.4) / (0.8 * 0.4 + 0.1 * 0.3 + 0.2 * 0.3) = 0.36

类似地，我们可以计算处于状态 B 和 C 的后验概率为：

P(B | A -> B) = (0.1 * 0.3) / (0.8 * 0.4 + 0.1 * 0.3 + 0.2 * 0.3) = 0.09
.
期望最大化（EM）算法：为了利用 EM 对马尔可夫链进行概率估算，您需要观察一段时间内马尔可夫链状态之间的转换。自该数据，您就可以利用 EM 算法根据观测数据迭代优化估算值来估算转移概率。 EM 算法通过在两个步骤之间交替工作：期望步骤（E-步骤），和最大化步长（M-步骤）。在 E-步骤中，根据参数的当前估算值，估算完整数据对数似然的期望值。在 M-步骤中，最大化相对于参数的完整数据对数似然的期望值，从而获得参数的更新估算值。然后您重复这些步骤，直到参数的估算值收敛到稳定值。例如，如果您观察到具有三种状态（A、B 和 C）的马尔可夫链，并希望估算状态之间的转移概率，则可以利用 EM 算法根据观察到的数据迭代优化转移概率的估计值。
利用 EM 进行概率估算的主要优点是它可以处理不完整或嘈杂的数据，并且可以估算统计模型的参数，即使底层分布不完全已知。然而，EM 可能对初始值很敏感，并且可能并不会始终收敛到对数似然函数的全局最大值。它也可能是计算密集型的，因为它需要反复估算对数似然函数及其梯度。
参数估计：为了将参数概率估算与马尔可夫链一起使用，您需要观察一段时间内马尔可夫链状态之间的转换。自该数据，您可以通过假设底层分布服从特定分布（例如正态分布或二项分布）来将参数模型拟合到转移概率。然后，您就能利用此模型来估算从一种状态转换到另一种状态的概率。例如，如果您观察到具有三种状态（A、B 和 C）的马尔可夫链，并发现从状态 A 到状态 B 的转换在总共 10 次转换中发生了 20 次，则可以将二项式模型拟合到数据，并采用它来估算从状态 A 过渡到状态 B 的概率。
参数概率估算的主要优点是它可以比非参数方法更准确，非参数方法不会对底层分布做出任何假设。然而，它需要对底层分布做出假设，这也许并不总是合适的，或可能导致估算偏差。此外，与非参数方法相比，参数方法可能不太灵活，健壮性也较差，因为它们对于假设分布的偏差很敏感。
非参数估算：为了将非参数概率估算与马尔可夫链一起使用，您需要观察一段时间内马尔可夫链状态之间的转换。自该数据，您可以通过计算转换发生的次数，并将其除以转换总数，来估算从一个状态转换到另一个状态的概率。例如，如果您观察具有三种状态（A、B 和 C）的马尔可夫链，并发现从状态 A 到状态 B 的转换在总共 10 次转换中发生了 20 次，则可以估算出从状态 A 过渡到状态 B 的概率为 0.5。
这种概率估算方法称为经验分布方法，它可用于估算任何事件集的概率，而不仅仅是马尔可夫链中的转换。非参数概率估算的主要优点是它不需要对底层分布进行任何假设，使其成为估算概率的灵活而稳健的方法。然而，它可能不如参数方法准确，参数方法对底层分布做出假设，如此才能更精确地估算概率。
自举（Bootstrapping）：这是一种通用技术，可用于估算马尔可夫链或任何其他概率模型中的概率。基本思想是采取少量观测值来估算系统状态的概率分布，然后依据该分布生成大量综合观测值。然后可以依据合成观测值更准确地估算概率分布，并且可以重复该过程，直至达到所需的精度水平。
为了在马尔可夫链中采用自举进行概率估算，您首先需要有一个初始马尔可夫链及其状态。与贝叶斯方法一样，自举更新，并改进了现有的马尔可夫链。链中的每个状态都与过渡到其它状态的概率相关联，并且不同状态对之间转换的概率与系统的历史无关。一旦得到初始马尔可夫链后，就可用自举来估算其状态的概率分布。为此，您需要始自对系统的少量观察，例如一些初始状态配置，或状态之间的简短转换序列。然后，您就可用这些观测值来估算系统状态的概率分布。

例如，如果您有一个具有三个状态 A、B 和 C 的马尔可夫链，并且您已经观察到系统从状态 A 过渡到状态 B 若干次，从状态 B 转换到状态 C 若干次，则可以依据这些观测值来估算从状态 A 过渡到状态 B，以及从状态 B 过渡到状态 C 的概率。

估计您有了系统状态的概率分布后，您就可用它来生成系统的大量综合观测值。这可以通过从概率分布中随机抽样来模拟状态之间的转换来完成。您然后就可用综合观测值更准确地估算概率分布，并重复该过程，直至达到所需的精度级别。

自举是估算马尔可夫链概率的实用技术，因为它允许您采取少量观测值生成大量综合观测值，从而提高估算值的准确性。它的实现也相对简单，可以与各种概率模型一起使用。不过，重要的是要注意，利用自举得到的估算准确性将取决于初始观测值的品质和底层概率模型，并且可能并非始终像其它估算技术那样准确。
Jackknife 估算：这种方法涉及运行马尔可夫链的多次模拟，每次都省略掉不同的状态或状态组。然后，通过求每个模拟中事件发生的概率平均值来估算事件发生的概率。以下是该过程的更详细说明：
- 设置马尔可夫链，并定义感兴趣的事件。例如，事件可能正达链中的某个状态，或者在两个特定状态之间转换。
- 运行马尔可夫链的多个模拟，每次都省略不同的状态或状态组。这可以通过在运行模拟时不考虑已排除的状态，或将其转换概率设置为零来完成。
- 对于每个模拟，计算事件发生的概率。这可以通过执行详细的平衡分析、或使用蒙特卡罗采样、或矩阵乘法、等技术来完成。
- 求每个模拟中事件发生的概率均值，从而得到事件在整个马尔可夫链中发生的概率的估算值。
在马尔可夫链中使用 jackknife 方法进行概率估算有几个优点。一个优点是，它允许更准确地估算事件发生的概率，因为它参考了每个单独状态对总体概率的影响。另一个优点是它实现起来相对简单，并且可以轻松自动化。不过，jackknife 方法也有一些限制。一个限制是它需要多次运行马尔可夫链的模拟，这对于大型或复杂链可能导致计算密集。此外，估算的准确性可能取决于模拟中排除的状态的数量和选择。
交叉验证：此方法可用于估算马尔可夫链中特定事件发生的概率。它涉及将数据划分为多个折叠或子集，并将每个折叠用作测试集，来评估模型在该子集上的性能。为了将交叉验证概率估算与马尔可夫链一起使用，我们首先需要设置具有所需状态和转换的马尔可夫链。然后，我们将数据划分为所需的折叠数。接下来，我们将遍历每个折叠，并将其用作测试集，来评估模型在该子集上的性能。这将涉及使用马尔可夫链来估算测试集中每个事件发生的概率，并将这些估算值与测试集中的实际结果进行比较。
最后，我们将对所有折叠的性能进行平均，以获得模型性能的总体估算。这对于评估模型的性能，并微调马尔可夫链的参数，以便提高其精度非常实用。务必注意的重点，为了将交叉验证概率估算与马尔可夫链一起使用，数据必须独立，且分布雷同，这意味着每个数据子集都应代表整个数据集。

这些方法中的每一种都有自己的优势和局限性，方法的选择将取决于数据的具体特征和分析目标。

利用 MQL5 向导实现

为了编写马尔可夫链的信号类实现，我们将使用在 “alglib” 文件夹下 “dataanalysis.mqh” 文件中的 “CMarkovCPD” 类。因此，我们的链在建模时作为离散时间链。这些离散时间链将有 5 个状态，这些状态只是收盘价的最后 5 个变化。如此，测试或运行智能系统的时间帧将定义为离散时间单位。为了估算状态之间转换的概率，“CMarkovCPD” 类需要添加轨迹，以便训练模型。添加的轨迹数是输入的可优化参数 “m_signal_tracks”。这就是我们如何初始化模式和添加轨迹（训练数据）的。

      CMCPDState _s;
      CMatrixDouble _xy,_p;
      CMCPDReport _rep;
      int _k=m_signal_tracks;
      
      _xy.Resize(m_signal_tracks,__S_STATES);
      
      m_close.Refresh(-1);
      
      for(int t=0;t<m_signal_tracks;t++)
      {
         for(int s=0;s<__S_STATES;s++)
         {
            _xy[t].Set(s,GetState(Close(Index+t+s)-Close(Index+t+s+1),Close(Index+t+s+1)-Close(Index+t+s+2)));
         }
      }

收盘价数据围绕 1.0 常规化。如果收盘价的变化为负，则输入数据小于 1.0；另一方面，如果为正，则输入将大于 1.0；若没有变化，正好为 1.0。这种规范化是通过如下所示的 “GetState” 函数完成的。

//+------------------------------------------------------------------+
//| Normalizer.                                                      |
//+------------------------------------------------------------------+
double CSignalMC::GetState(double NewChange,double OldChange)
   {
      double _state=0.0;
      
      double _norm=fabs(NewChange)/fmax(m_symbol.Point(),fabs(NewChange)+fabs(OldChange));
      
      if(NewChange>0.0)
      {
         _state=_norm+1.0;
      }
      else if(NewChange<0.0)
      {
         _state=1.0-_norm;
      }
      
      return(_state);
   }

一旦添加数据之后，我们需要初始化 “CMCPDState” 类的实例，因为这是处理所有模型数据，并帮助计算概率估算的对象。我们是这样做的：

      CPD.MCPDCreate(__S_STATES,_s);
      
      CPD.MCPDAddTrack(_s,_xy,_k);
      
      CPD.MCPDSetTikhonovRegularizer(_s,m_signal_regulizer);
      
      CPD.MCPDSolve(_s);
      
      CPD.MCPDResults(_s,_p,_rep);

理想情况下，“m_signal_regulazier” 输入参数不应是抽象的双精度值，而应是代表 track 数据量级的双精度值。换句话说，它应该与从 “GetState” 函数获得的轨迹数据成比例。这意味着，如果您的理想是将其优化为在 0.5-0.0 之间，则在使用 Tikhonov 调节器时，您应该将其乘以最大轨迹数据的量级。

“_p” 矩阵是我们的过渡矩阵，具有状态之间转换的所有概率。信号类的完整代码附在文章末尾。

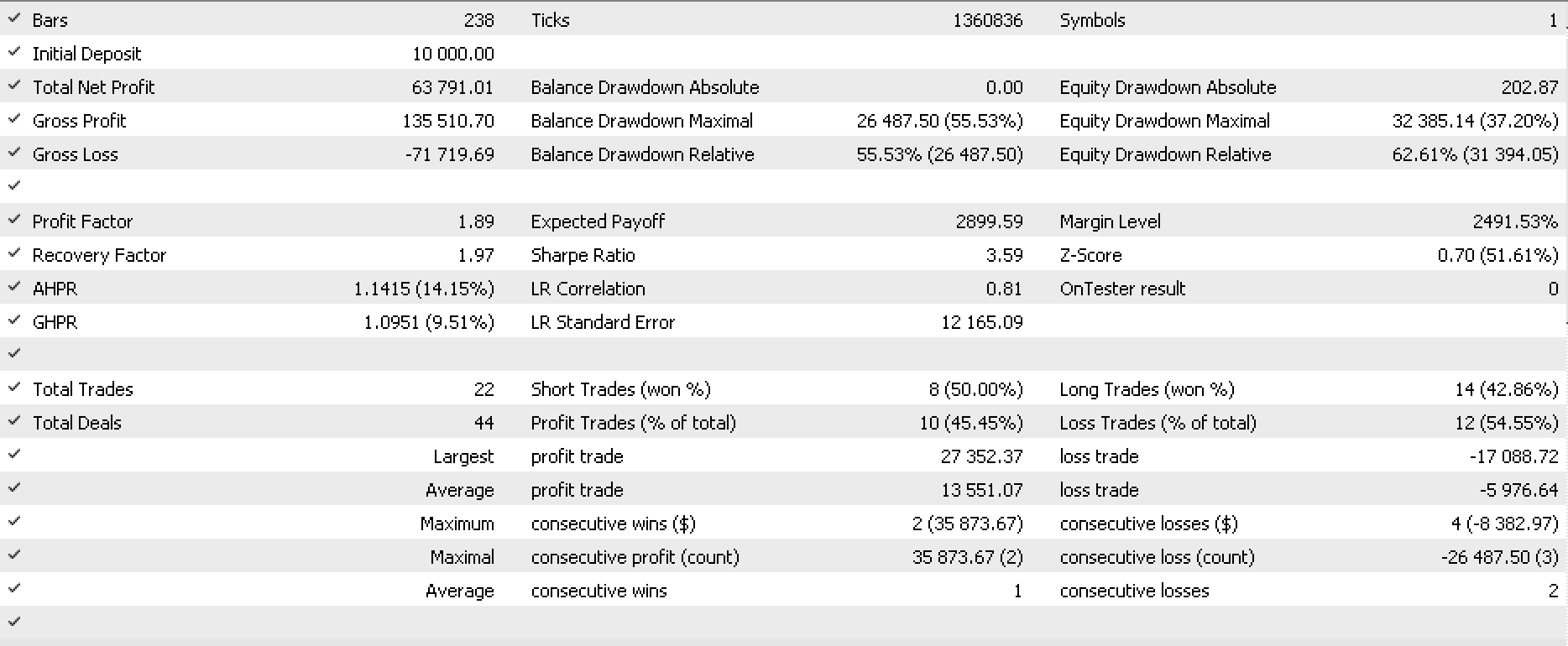
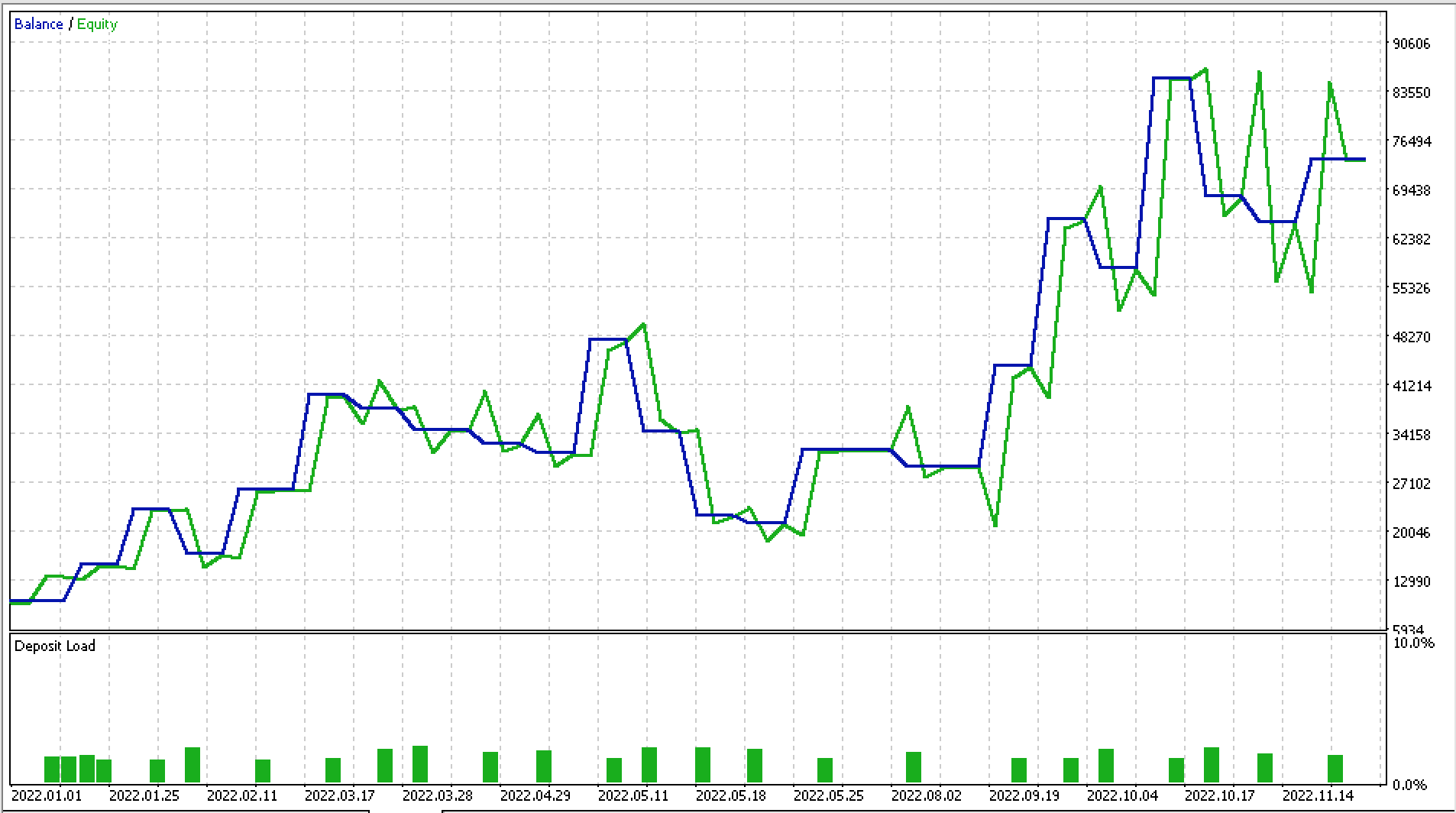
我针对 2022 年的 EURJPY，日线时间帧内进行了一些测试，以下是报告，和随之而来的净值曲线的一部分。