Combinatória e teoria da probabilidade para negociação (Parte III): primeiro modelo matemático

MetaTrader 5 — Negociação | 11 outubro 2021, 08:33

654

Evgeniy Ilin

Sumário

Introdução

No último artigo, consegui a primeira fórmula para fractais, o que me permitia supor que era perfeitamente possível descrever todos os valores relevantes que descrevem um fractal usando um modelo matemático. A simulação não pretendia descrever esses valores, apenas ajudou na coleta dos primeiros dados para poder analisar mais profundamente essas estruturas. Neste artigo, decidi dar atenção especial à descrição de todo o processo de desenvolvimento do primeiro modelo matemático até a obtenção do próprio modelo matemático, que pode ser usado em diversos EAs.

Novas ideias

Ao considerar o fractal simétrico visto no artigo anterior, consegui uma fórmula geral para calcular o número médio de etapas que o preço percorre como resultado do movimento dentro de um determinado corredor, que é determinado pelo número dos mesmos corredores simétricos e menores . Aqui está a fórmula:

S = K^2 - número médio de etapas no novo corredor, com base no fato de que uma etapa é outro corredor
P = K * P0 --> K = P/P0 - quantas vezes o corredor conhecido é maior que o desconhecido
P - largura do corredor cujo número médio de etapas é desconhecido (as etapas têm metade do tamanho do corredor inicial)
P0 - largura do corredor conhecido

Para descrever um corredor assimétrico, é necessário redefinir alguns dos conceitos acima, para que se tornem mais compreensíveis. O mais importante aqui é "K" Na verdade, esse número reflete o número de etapas que o preço precisa percorrer num novo corredor, desde que as etapas ocorram apenas para cima ou apenas para baixo. Para um corredor simétrico, é intuitivamente claro que não importa qual limite estamos considerando (cruzando), inferior ou superior, o número de etapas dado terá o mesmo valor em vista da espelhamento deste problema, tanto para o limite superior quanto para o inferior. No caso de assimetria, obtive, como resultado de experimentos com o código do artigo anterior, que o número médio de etapas para este caso é determinado da seguinte forma:

S = n * m - número médio de etapas para o caso de metades assimétricas do corredor
n - número de etapas que cabem na metade superior do corredor
m - número de etapas que cabem na metade inferior do corredor

Logo, é claro que, no caso de um corredor simétrico, obtemos que: "m = n". Bem, e com base nisso:

S = n * n = m * m = m * n = n^2 = m^2 = K^2
K = n = m

Ou seja, a primeira fórmula que defini é apenas um caso especial da anterior, e "K" não é mais necessário.

Uma característica interessante desta função é o fato de S(a*k, b*k) = S(a,b) * S(k,k), o que é muito fácil de provar:

S(n*k ,m*b) = m*k*n*b = n*m * k*b
S(n ,m) * S(k ,b) = n*m * k*b

Esta propriedade é muito interessante se olharmos e pensarmos sobre ela corretamente. Claro, ele não sugere alguma ideia de uma vez, mas junto com reflexões adicionais pode fornecer a definição de todas as fórmulas necessárias para descrever todo o fractal. Esta propriedade apenas reflete uma propriedade muito importante de qualquer fractal - a possibilidade de aninhamento. Em outras palavras, qualquer fractal finito de grande complexidade pode ser representado como dois ou mais fractais simples que desempenham o papel de etapas um dentro do outro. Esta propriedade ainda é necessária para generalizar esta fórmula para casos mais complexos.

Antes de avançar e reflexionar, é necessário lembrar que as fórmulas que foram definidas acima funcionam apenas no caso de “p=0,5”. Assim que os parâmetros do mercado ou nosso fractal começam a se desviar de um passeio aleatório, esta fórmula começa a mudar de forma muito interessante, assim:

Ss[n,m,p] – fórmula mais geral para o número médio de etapas (em qualquer direção)
S(n ,m) = Ss[n,m,0,5] – fórmula para um passeio aleatório é um caso especial da fórmula geral

Fórmula geral para o número médio de etapas e suas consequências

Para determinar como seria uma fórmula mais geral, usei a invariância do princípio de aninhamento do fractal. É interessante que, se considerarmos qualquer nível particular de aninhamento do fractal em relação ao anterior, podemos evitar pensar em que etapas ocorreram numa etapa particular. Isso significa que as etapas primárias para cima e para baixo ocorrem precisamente com aquelas proporções de frequências que correspondiam à situação do nível anterior. Em outras palavras, quando é cruzado um dos limites do nível de aninhamento correspondente é porque isto é uma etapa para cima ou uma etapa para baixo para o próximo nível de aninhamento depois dele. Mas também se sabe que a razão da frequência de ocorrência de etapas para o nível de aninhamento atual não dependerá da configuração do nível atual. Isso significa que o princípio de aninhamento de fractais é observado para qualquer probabilidade “p”. Isso, por sua vez, nos diz que quando o valor de “p” muda, nossa fórmula deve mudar, mas de alguma forma retém sua propriedade de aninhamento. Um experimento simples pode nos ajudar a determinar o tipo de fórmula geral. Sabemos que a probabilidade “p” tem um ponto de passeio aleatório e mais dois pontos extremos com zero e um. Vamos considerar quais valores nossa função assumirá nesses três pontos. Depois de analisar os resultados dos cálculos, como resultado, obtemos o seguinte:

Ss[n,m,1] = Sn[n] = n
Ss[n,m,0] = Sm[m] = m
Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
Sn[n,p] – número de etapas indo numa direção até a borda superior
Sn[m,p] – número de etapas numa direção até a borda inferior

É fácil adivinhar que no primeiro caso não temos absolutamente nenhuma descida e todas as cadeias seguem o mesmo caminho, e já no segundo tudo é igual só que é o contrário, as etapas apenas descerão. Pode-se observar que em valores extremos, um dos fatores parece desaparecer completamente da fórmula. Isso é possível se aumentarmos para zero. A potência zero converte qualquer número em um. Além disso, a potência tem uma invariância da forma:

A^X * B^X = (A*B)^X

Se imaginarmos que, em vez desses números, são nossas etapas médias, isso significa que ambos manteremos o princípio de aninhamento de fractais funcionando, e podemos entender que esta potência não depende de “n e m”. Como resultado, a fórmula geral para o número médio de etapas será:

Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

Se descrevermos esquematicamente como será o princípio de aninhamento de fractais, poderemos representá-lo assim:

Cadeias de produtos

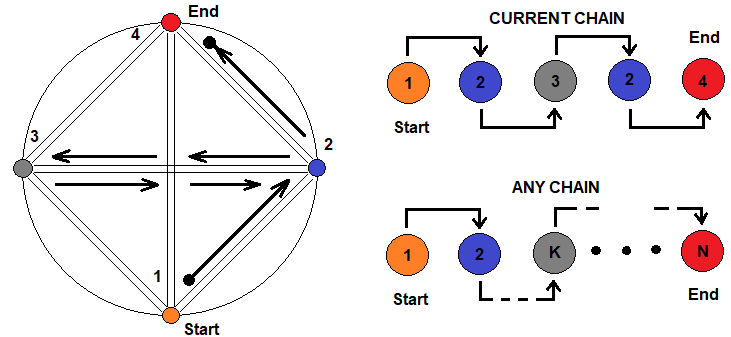
A figura mostra quatro estados que representam diferentes fractais, que podem ser expressos um através do outro. A transição de um estado para outro é possível usando qualquer cadeia. À direita vemos uma cadeia escolhida arbitrariamente, e um pouco abaixo é mostrado que ela pode ser de qualquer comprimento e complexidade, e podemos passar pelo mesmo estado um número ilimitado de vezes. Tudo isso significa que a fórmula de cálculo do número médio de etapas do fractal pode ser representada como uma cadeia de produtos que representam os níveis de aninhamento dos fractais.

Construindo um protótipo de função de potência

O que acontecerá a seguir vem da propriedade de aninhamento dos fractais e da invariância das funções de potência com o mesmo grau, em relação à base. Todos esses princípios matemáticos nos ajudarão no futuro a derivar fórmulas para uma descrição mais profunda dos fractais. Acontece que obtemos duas funções adicionais, cuja forma não conhecemos:

Pn[p] – potência para o multiplicador do limite superior
Pm[p] – potência para o multiplicador do limite inferior

Mas sabemos que:

Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

Se entendemos as funções de potência, podemos construir um protótipo adequado para essa função. Eu escolhi este protótipo:

Pn[p] = 1 , if p >= 0.5
Pn[p] = ( (1 – p)/0.5 ) ^ K
Pm[p] = 1 , if p <= 0.5
Pm[p] = ( p/0.5 ) ^ K
K – potência que regula quão plana é a função

Na verdade, seria mais preciso representar “2” e “4” na forma de polinômios que podem descrever com mais precisão a transição suave de uma determinada potência, mas acho que isso é redundante. Se alguém quiser definir polinômios mais precisos, aqui estão os protótipos para eles:

Pn[p] = C1 * ( (1 – p)/0.5 ) ^ K1 + C2 * ( (1 – p)/0.5 ) ^ K2 … + … + CN * ( (1 – p)/0.5 ) *KN
Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 … + … + CN * ( p/0.5 ) ^ KN
С1 + С2 + … + … СN = 1 – coeficientes de peso da potência correspondente
KN – potência do termo correspondente

Se olharmos atentamente para o polinômio geral, podemos entender que o polinômio que escolhi é a versão mais simples do geral, com um único termo. Todos os princípios aqui apresentados podem ser verificados revisando o “n, m” fracionário, que será, ao mesmo tempo, confirmação indireta adicional do acima mencionado.

Para testar essas suposições, criei o seguinte programa:

Validação de fórmula

Como pode ser visto nos resultados do programa, tudo funciona da maneira que precisamos e isso é suficiente. Para ter certeza disso, basta comparar dois números, caso sejam coincidentes, confirma-se o princípio de aninhamento e a possibilidade de uso de números fracionários “n,m”.

Esquema geral para obter a melhor função a partir de uma família limitada por protótipo

Confirmado o princípio de aninhamento, é necessário decidir como será feita a busca dos coeficientes necessários para o protótipo. Eu escolhi o tipo de pesquisa mais simples e compreensível, nomeadamente a geração de números aleatórios na faixa necessária. O esquema deste método é assim:

Esquema aproximador

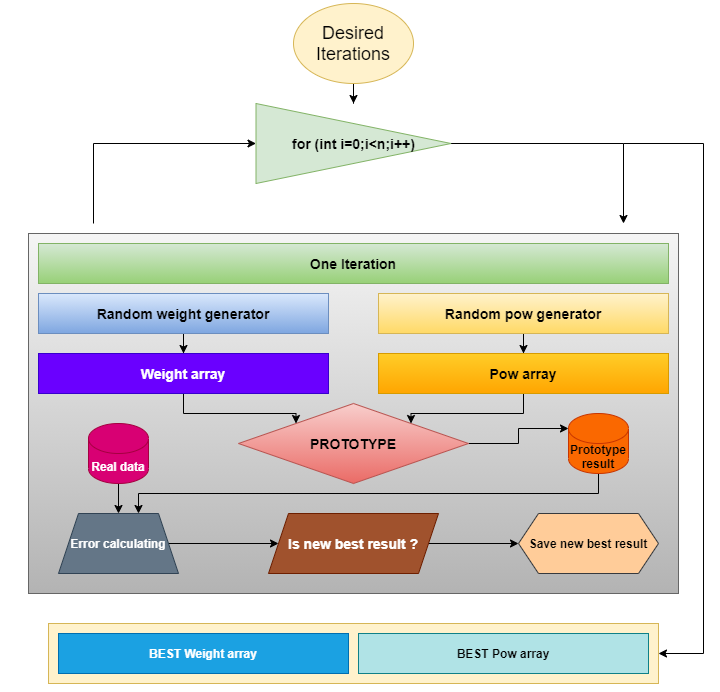
A melhor parte é que esse esquema é adequado para qualquer protótipo de função cujos coeficientes precisam ser selecionados para um melhor ajuste dos dados reais com o modelo matemático. Este esquema será válido posteriormente, pois no final do artigo aplicaremos o mesmo método para processar outro protótipo.

Análise profunda

Agora vamos fazer uma análise mais profunda da estrutura desta fórmula e o que ela descreve. O resultado da fórmula é o número médio de etapas pelas quais o preço passa antes de cruzar um dos limites. Nesse caso, as etapas para cima e para baixo são consideradas iguais, mas na realidade essa igualdade só é possível no caso de um passeio aleatório. Para uma descrição completa de um fractal assimétrico, isso não é suficiente, e é necessário determinar em que realmente consiste o valor dado. É intuitivamente claro que, em teoria, o número médio de etapas, independentemente do tipo, depende tanto do número médio de etapas ao cruzar o limite superior quanto do número médio de etapas ao cruzar o limite inferior. Vamos apresentar esses valores primeiro para o caso de cruzar o limite superior:

SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
S[U] - número médio de etapas, não importa quais, desde que a cadeia de etapas atinja primeiro o limite superior
S[U,u] - número médio de etapas para cima, desde que a cadeia de etapas atinja primeiro o limite superior
S[U,d] - número médio de etapas para baixo, desde que a cadeia de etapas atinja primeiro o limite inferior
P[U] - probabilidade de que o limite superior seja cruzado primeiro
SP[U,ud] - número probabilístico médio de etapas para cruzar o limite superior

Para cruzar a borda inferior, as fórmulas serão semelhantes:

SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
S[D] - número médio de etapas não importa, desde que a cadeia de etapas tenha primeiro atingido o limite inferior
S[D,u] - número médio de etapas para cima, desde que a cadeia de etapas atinja primeiro o limite inferior
S[D,d] – número médio de etapas para baixo, desde que a cadeia de etapas atinja primeiro o limite inferior
P[D] - probabilidade de que o limite inferior seja cruzado primeiro
SP[D,ud] - número probabilístico médio de etapas para cruzar o limite inferior

E é claro que:

S = SP[U,ud] + SP[D,ud]

Para simplificar toda a abordagem, o resultado de todas essas estimativas é que todos os valores resultantes dependem de cinco valores fundamentais:

S[U,u] = SP[U,u]/P[U] - número médio de etapas para cima, desde que a cadeia de etapas atinja primeiro o limite superior
S[U,d] = SP[U,d]/P[U] - número médio de etapas para baixo, desde que a cadeia de etapas atinja primeiro o limite superior
S[D,u] = SP[D,u]/P[D] - número médio de etapas para cima, desde que a cadeia de etapas atinja primeiro o limite inferior
S[D,d] = SP[D,d]/P[D] - número médio de etapas para cima, desde que a cadeia de etapas atinja primeiro o limite inferior
P[U] - probabilidade de que o limite superior seja cruzado primeiro

Procuraremos as fórmulas para dados valores com base nos resultados da operação fractal com diferentes parâmetros de entrada. No último artigo, escolhi os seguintes valores como saída do fractal:

SP[U,u] – número probabilístico médio de etapas para cima, desde que a cadeia de etapas atinja primeiro o limite superior
SP[U,d] – número probabilístico médio de etapas para baixo, desde que a cadeia de etapas atinja primeiro o limite superior
SP[D,u] – número probabilístico médio de etapas para cima, desde que a cadeia de etapas atinja primeiro o limite inferior
SP[D,d] – número probabilístico médio de etapas para baixo, desde que a cadeia de etapas atinja primeiro o limite inferior
P[U] - probabilidade de que o limite superior seja cruzado primeiro
P[D] - probabilidade de que o limite inferior seja cruzado primeiro
S = SP - número médio de quaisquer etapas

Vou agrupar separadamente os elementos que podem ser expressos em termos de valores fundamentais:

SP[U]
S[U,ud] = S[U,u] + S[U,d]
S[D,ud] = S[D,u] + S[D,d]
P[D] = 1 – P[U]
S = SP[U,ud] + SP[D,ud]

Para ter a chance de entender a matemática dos fractais, realizei uma análise bastante extensa e, em suma, tudo pode ser colocado junto num esquema bastante compacto que reflete todo o processo de busca do modelo matemático que obtive:

Sequência de pesquisa de modelo matemático

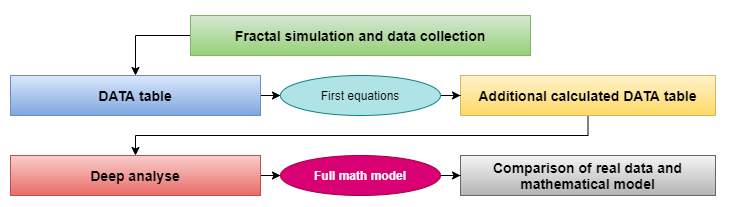
Coleta de dados e conclusões

Como resultado de um exame mais detalhado dos resultados do cálculo do fractal, foi notado que os seis valores que inicialmente determinei ao construir o conceito de um fractal universal estão matematicamente relacionados. Inicialmente, efetuei testes em limites simétricos e tentei isolar dependências entre dados valores, e algo deu certo. Fiz os cálculos para dez casos diferentes:

Índice de teste	Etapas na metade superior do corredor (n)	Etapas na metade inferior do corredor ( m )	Probabilidade de etapa inicial ( p )	Número probabilístico médio de etapas superiores para o limite superior ( SP[U,u] )	Número probabilístico médio de etapas inferiores para o limite superior ( SP[U,d] )	Número probabilístico médio de etapas superiores para o limite inferior ( SP[D,u] )	Número probabilístico médio de etapas inferiores para o limite inferior ( SP[D,d] )	Número probabilístico médio de quaisquer etapas para o limite superior ( SP[U,ud] )	Número probabilístico médio de quaisquer etapas para o limite inferior ( SP[D,ud] )
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1.25	0.5	0.25	1	1.75	1.25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

Abaixo está uma tabela com valores calculados que não são exibidos no log do fractal. Precisaremos deles para avaliar as dependências entre os valores:

Índice de teste	Etapas na metade superior do corredor (n)	Etapas na metade inferior do corredor ( m )	Probabilidade de cruzamento de limite superior ( P(U) )	Probabilidade de cruzamento de limite inferior ( P(D) )	Número médio de quaisquer etapas ao cruzar o limite superior (S[U,ud]) = SP[U,ud]/P[U]	Número médio de quaisquer etapas ao cruzar o limite inferior (S[D,ud]) = SP[D,ud]/P[D]	Média de degraus superiores para o limite superior ( S[U,u] ) = SP[U,u]/P[U]	Número médio de degraus inferiores para o limite superior ( S[U,d] ) = SP[U,d]/P[U]	Número médio de etapas superiores para o limite inferior ( S[D,u] ) = SP[D,u]/(P[D])	Quantidade média etapas inferiores para o limite inferior ( S[D,d] ) = SP[D,d]/(P[D])	Número médio de etapas ( S )
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

Depois de estudar cuidadosamente esta tabela, podemos encontrar as duas primeiras equações de que precisamos para calcular todas as quatro incógnitas, das quais todas as outras quantidades são compostas. Podemos obter essas fórmulas prestando atenção nas colunas “S[U,u], S[U,d], S[D,u], S[D,d]”. É muito interessante que os números aí obtidos tenham a mesma parte fracionária aos pares nas colunas “S[U,u], S[U,d]” e em “ S[D,u], S[D,d]”. Entre outras coisas, pode-se verificar que “S[U,u] > S[U,d]” и “S[D,d] > S[D,u]”. Se subtrairmos esses valores em pares e compararmos com "m, n", então verifica-se que essa diferença é exatamente igual ao número correspondente de etapas para o limite superior ou inferior:

S[U,u] – S[U,d] = n
S[D,d] – S[D,u] = m

Assim, obtemos duas equações muito importantes que nos ajudarão na definição das valores fundamentais. Claro, duas equações não são suficientes para isso, por isso podemos obter mais duas equações que permitirão determinar todas os mesmos valores, procedendo apenas de uma lógica ligeiramente diferente. Partindo do fato de que, se realizarmos experimentos com um fractal por um tempo infinitamente longo, então se perguntarmos sobre a razão da frequência de ocorrência de etapas para cima e para baixo, então será fácil adivinhar que essas frequências são proporcionais a as probabilidades correspondentes.

Essas proporções podem ser obtidas se supomos:

Lim[N0 -- > +infinity] (N0[U]/N0) = p
Lim[N0 -- > +infinity] (N0[D]/N0) = 1-p
Lim[N0 -- > +infinity] (N0[U]/N) = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = S[UD,d]
Lim[N0 -- > +infinity] (N0/N) = S
N0 - número de experimentos elementares realizados com as etapas iniciais (formam uma experiência complexa)
N - número de experimentos complexos que são compostos de simples

Se inserirmos o multiplicador “N0/N0 = 1” em “3” e “4” e organizar corretamente as frações dentro, obteremos:

Lim[N0 -- > +infinity] (N0[U]/N) = Lim[N0 -- > +infinity] (N0[U]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[U]/N0) * Lim[N0 -- > +infinity] (N0/N) = p*S = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = Lim[N0 -- > +infinity] (N0[D]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[D]/N0) * Lim[N0 -- > +infinity] (N0/N) = (p-1)*S = S[UD,d]

O limite do produto pode ser representado como o produto dos limites, se cada um desses limites for um número finito e não for para mais ou menos infinito. Nesse caso, é claro que ambos os limites são exatamente isso. É assim que essas fórmulas são definidas. Como resultado, obtemos as fórmulas correspondentes:

S[UD,u] = S*p
S[UD,d] = S*(1-p)

É melhor expressar esses valores em termos de fundamental, obteremos duas equações ausentes para determinar tudo o que precisamos:

S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)

Como resultado, descobrimos que existem cinco incógnitas nas quatro equações. A quinta incógnita é uma das probabilidades que formam um grupo completo (as probabilidades de atingir um dos limites). Para poder encontrar todas as cinco incógnitas, devemos obter a quinta equação, porque um sistema de equações só pode ter uma solução única se o número de equações for igual ao número de incógnitas. A quinta equação pode ser obtida intuitivamente se soubermos qual é a diferença entre as etapas superior e inferior. Idealmente, este é o limite:

Lim[Nt[U] -- > +infinity] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
Nt[U] = - número ideal de etapas básicas calculadas usando a probabilidade de uma etapa básica para cima
Nt[D] - número ideal de etapas básicas calculado usando a probabilidade de etapa básica para baixo
N0[U] - número real de etapas básicas para cima
N0[D] - número real de etapas básicas para baixo

Da mesma forma, você pode encontrar um limite semelhante usando as probabilidades de cruzar os limites:

Lim[Nb[U] -- > +infinity] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
Nb[U] - número ideal de etapas básicas para cima, calculado usando a probabilidade de cruzar o limite superior
Nb[D] - número ideal de etapas básicas para baixo, calculado usando a probabilidade de cruzar o limite inferior
N0[U] - número real de etapas básicas para cima
N0[D] - número real de etapas básicas para baixo

A partir desses dois limites, podemos fazer um mais complexo, por exemplo, sua soma, diferença ou produto ou quociente. Escolherei o quociente, assim a expressão a seguir será reduzida, o que nos salvará completamente do limite “N0[U] - N0[D]”. Como resultado, dividindo os limites e transformando a equação, obtemos o seguinte:

P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S

Esta será a nossa quinta equação, a partir da qual será possível encontrar imediatamente as probabilidades de cruzar os limites. Como resultado, obtemos um sistema de cinco equações. É assim que vai ficar:

S[U,u] – S[U,d] = n
S[D,d] – S[D,u] = m
S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)
P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

A propósito, é interessante que o sistema original de equações de quatro incógnitas apenas leva à mesma equação no final. Podemos resolver este sistema da maneira clássica, eliminando sucessivamente as variáveis:

--> S[U,u] = n + S[U,d] – excluímos “S[U,u]”
--> S[D,d] = m + S[D,u] – excluímos “S[D,d]”
(n + S[U,d]) * P[U] + S[D,u] * ( 1 – P[U] ) = S*p – substituímos tudo na equação “3”
S[U,d] * P[U] + (m + S[D,u]) * ( 1 – P[U] ) = S*(1-p) – substituímos tudo na equação “4”

Após essas transformações, resta subtrair a equação “3” de “4”, e obtemos a mesma equação que obtivemos intuitivamente, confirmando assim tanto o sistema de equações que recebemos inicialmente. Mas, infelizmente, esse sistema é organizado de forma que não podemos obter os quatro valores restantes dele. Inicialmente, presumi que esse sistema ainda fornecerá tudo o que você precisa, mas não. Para entender o que está faltando, tive que analisar a tabela de dados fractais e identificar consistentemente a fórmula para um desses quatro valores. É muito bom que, tendo encontrado uma fórmula para um desses valores, possamos usar o sistema resultante para encontrar todos os outros valores. No entanto, o sistema é útil.

Algoritmo para calcular todo o modelo matemático

Primeiro, vamos definir as equações inversas e a sua sequência de uso para, sabendo “S[U,u]”, encontrar todos os outros valores. Escolhi esse valor porque consegui encontrar fórmulas para calcular esse valor. Se o usarmos, poderemos encontrar imediatamente o valor “S[U,d]” usando a primeira equação:

S[U,d] = S[U,u] – n

Em seguida, podemos substituir esses valores nas equações “3”, “4” e encontrar os valores ausentes “S[D,u]”, S[D.d]. O valor “S[D,u]” pode ser calculado imediatamente a partir da terceira equação:

S[D,u] = ( S*p – S[U,u] * P[U] ) / ( 1 – P[U] )

Resta obter uma fórmula para a última incógnita. Para fazer isso, substituímos a expressão obtida por "S[U,d]" na quarta equação:

S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 – P[U] ) = ( S*(1-p) - ( S[U,u] – n ) * P[U] ) / ( 1 – P[U] )

A única coisa que falta é o valor "P[U]", que pode ser facilmente obtido resolvendo a quinta equação. Vamos fazer isso:

P[U] * n – (1 - P[U]) * m = 2*p*S – S
--> P[U] * (n + m) = 2 * p * S – S + m
--> P[U] = ( 2 * p * S – S + m ) / (n + m)

Os valores conhecidos neste caso são os seguintes números:

n - número de etapas superiores para o limite superior
m - número de etapas inferiores para o limite inferior
p - probabilidade do etapa inicial para cima
S[U,u] – número médio de etapas superiores, desde que o limite superior seja cruzado
P[U] - probabilidade de cruzar o limite superior

O valor “4” é calculado conforme já definimos:

S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
Pn[p] = 1 , if p >= 0.5
Pn[p] = ( (1 – p)/0.5 ) ^ K
Pm[p] = 1 , if p <= 0.5
Pm[p] = ( p/0.5 ) ^ K
K – potência que regula quão plana é a função

Iremos calcular o coeficiente de "planura" num programa separado um pouco mais tarde. Resta determinar o valor calculado mais importante. Como resultado da análise do valor tabular "S[U,u]" para limites simétricos, identifiquei fórmulas até mesmo para dois valores:

S[U,u] = Summ[ i = 0, n] ( i ) ; if n == m
S[U,d] = Summ[ i = 0, n] ( i-1 ) ; if n == m

O problema é que essas fórmulas funcionam apenas para “p = 0,5” e limites simétricos. É necessário expandir o conceito dessas fórmulas para casos de limites assimétricos, e então será possível generalizá-lo para casos de diferentes valores de “p”. Antes de abordar tais generalizações, é importante notar que os resultados do teste na tabela se aplicam apenas aos casos “m > n”. No caso de “m < n”. As fórmulas já funcionarão para os valores“S[D,d], S[D,u]”. Nesse caso, é necessário criar um espelho análogo do algoritmo para encontrar todas as outras quantidades desconhecidas.

Da mesma forma, definiremos as equações inversas e sua sequência de uso, apenas levando em consideração que já estamos utilizando “ S[D,d] ”. Da mesma forma que no algoritmo anterior, encontraremos o valor “S[D,u]”, usando a segunda equação:

S[D,u] = S[D,d] – m

Em seguida, podemos substituir esses dois valores nas equações "3", "4" e encontrar os valores ausentes “S[U,u]”, S[U.d]. O valor “S[U,d]” pode ser calculado imediatamente a partir da quarta equação:

S[U,d] = ( S*(1-p) - S[D,d] * ( 1 – P[U] ) ) / P[U]

Resta obter uma fórmula para a última incógnita. Para fazer isso, substituímos a expressão obtida por “S[D,u]” na terceira equação:

S[U,u] = ( S*p – ( S[D,d] – m ) * ( 1 – P[U] ) ) / P[U]

Como resultado, obtivemos todos os dados necessários para generalizar as fórmulas “S[U,u], S[D,d]” para os casos “n != m”. Como resultado da análise dos dados da tabela, foram obtidos os seguintes dados:

m > n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i ) + (m-1)/3

E, claro, para o caso oposto:

m < n, p = 0,5
S[D,d] = Summ[ i = 0 … m] ( i ) + (n-1)/3

Para o caso padrão de limites simétricos, naturalmente, tudo isso será mais simples:

m = n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i )
S[D,d] = Summ[ i = 0 … m] ( i )

Protótipos para obter a última equação

Agora vamos definir um protótipo de uma função modificada que irá descrever “S[U,u], S[D,d]” para todos os valores possíveis de “p”. Para construir um protótipo básico funcional, precisamos de três pontos no eixo "p" e algumas suposições sobre a estrutura geral. Acredito que seja suficiente considerar dois tipos de função genérica:

Sp[U,u] = S[U,u] ^ K(p)
Sp[D,d] = S[D,d] ^ K(q)
q = 1-p

O primeiro tipo pode ser um protótipo de trabalho real e uma espécie de marcador de que a estrutura é diferente e uma lógica de pensamento diferente é necessária. Fiz isso e descobri que a função de energia é quase infalivelmente capaz de reunir todos os dados. Claro, podemos criar protótipos mais complexos, que estão mais próximos da verdade, mas acho que isso é redundante aqui. O mais importante é entender a lógica do pensamento, e se alguém quiser lapidar perfeitamente o modelo, isso será feito de forma muito simples, com base nos meus dados. Criei um programa de teste para este propósito:

Funções encontradas com base em protótipos

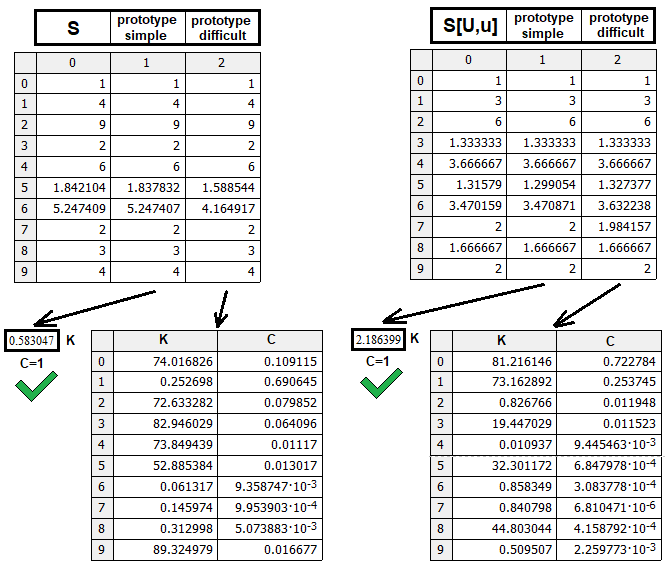
Aqui está uma verificação para ambos os protótipos “S(n,m,p), S[U,u](n,m,p) ”. A verificação do protótipo “S[D,d](n,m,p)” não é necessária, uma vez que esta função é espelhada em “S[U,u](n,m,p)” no sentido de que ”S[D,d](n,m,p) = S[U,u](m,n,p-1)”. Esta figura compara a qualidade dos protótipos encontrados em termos de eficiência. Para encontrá-los, cada protótipo foi testado com o mesmo número de combinações aleatórias de coeficientes de peso e potência na fórmula, e é natural que um protótipo mais simples com o mesmo número de ciclos de busca dê um resultado mais bonito. Mas, se quisermos, podemos fazer cálculos demorados e ver do que os protótipos mais complexos são capazes.

Após a verificação, devemos decidir sobre a estrutura interna da função aninhada “K(p)”, “K(q)”. Em primeiro lugar, sua estrutura interna deve garantir a coincidência obrigatória nos pontos “p=0, p=0.5, p=1”, q=0, q=0.5, q=1”. Conhecemos os valores da função nestes pontos, o que nos permitirá selecionar mais facilmente o protótipo desejado:

p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
p = 0.0 ; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
q = 1.0 ; Sp[D,d] = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-infinity) --> K(0.0) = -infinity

A primeira e a quarta expressões dizem que a potência deve ser igual a um no ponto do passeio aleatório. A segunda e a quinta expressões dizem que a potência deve ser tal que, quando elevado a ela, obtenhamos "n" ou "m", o que pode ser visto na tabela de resultados, que estava acima. E, finalmente, o terceiro e o sexto dizem que a potência deve tender a menos infinito para garantir zero. Este fato implica adicionalmente que os valores "p" e "q" devem estar no denominador do protótipo, porque normalmente a divisão por zero leva apenas a tais valores limites do tipo infinito. Já tínhamos experiência na construção de um protótipo de potência para uma função, ele pode ser tomado como base e retrabalhado. Depois de analisar profundamente o problema, cheguei a este protótipo:

K(p) = 1 + D * Summ(N) (Kn[0] * | (( p – 0.5 )/(0.5*p)) | ^ A[0] + Kn[1] * | (( p – 0.5 )/(0.5*p)) | ^ A[1] + …. + Kn[N] * | (( p – 0.5 )/(0.5*p)) | ^ A[N])
Kn[0] + Kn[1] + …. Kn[N] = Log[S[U,u]-->n] – 1
D = (( p – 0.5 )/(0.5*p)) / | (( p – 0.5 )/(0.5*p)) |
K(q) = 1 + C * Summ(N) (Km[0] * (( q – 0.5 )/(0.5*q)) ^ B[0] + Km[1] * (( q – 0.5 )/(0.5*q)) ^ B[1] + …. + Km[N] * (( q – 0.5 )/(0.5*q)) ^ B[N])
Km[0] + Km[1] + …. Km[N] = Log[S[D,d]-->m] – 1
C = (( q – 0.5 )/(0.5*q)) / | (( q – 0.5 )/(0.5*q)) |
Kn, Km - pesos dos termos correspondentes
A, B - sensibilidade dos termos

A função parece complicada, mas é construída com base em uma lógica simples. Com “p=0.5, q=0.5”, tudo sob o sinal da soma vira para zero e apenas permanece uma unidade, fornecendo assim as condições “1”, “4”. Se “p=1, q=1” as frações correspondentes dentro da soma são transformadas numa unidade, frações essas que são elevadas a uma potência: “|(( p – 0.5 )/(0.5*p)) |”. É importante notar que esses termos estão sob o sinal do módulo, de forma a excluir os valores complexos da função ao subir a uma potência, em vez disso, o sinal é levado em consideração como um fator adicional. A potência deixa de atuar nesses termos e toda a soma se transforma nos números “ Log[S[U,u]-->n] – 1, Log[S[D,D]-->m] - 1”. Somando este número com um, obtemos os valores requeridos da função: “Log[S[U,u]-->n], Log[S[D,d]-->m]”.

Os polinômios de interpolação são construídos de acordo com uma lógica semelhante, um exemplo da qual é o amplamente difundido e conhecido polinômio de Lagrange. Nosso polinômio é feito para uma tarefa específica e é aplicável apenas aqui, sua vantagem é a adaptabilidade máxima à tarefa. Para encontrar a função necessária de uma determinada família de curvas, você só precisa pegar duas matrizes de números.

Implementação e teste do modelo matemático

Graças às expressões obtidas, é muito fácil implementar a funcionalidade de cálculo de qualquer fractal. Precisamos apenas de uma estrutura, que será um contêiner com todos os dados que a função principal retornará. As outras funções serão auxiliares. Para nosso uso, precisamos apenas da última função:

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

Para verificar este modelo matemático, implementei um análogo deste código no MathCad15, se o modelo matemático for composto corretamente, os resultados da tabela coincidirão com o resultado que o modelo matemático nos retornará. Qualquer um pode ver a listagem deste programa, pois estará anexada ao artigo. Não dei esta listagem, porque vai ocupar muito espaço no artigo, mas com certeza você vai precisar ver o resultado. Vamos comparar as matrizes e ter certeza de que o modelo matemático é viável:

Verificando a precisão do modelo matemático

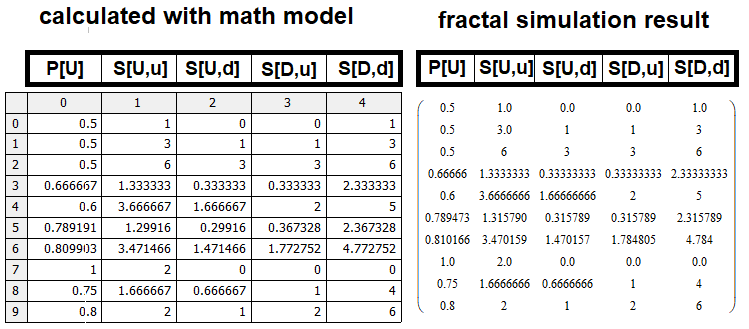
É claro que em alguns lugares existem pequenas rugosidades, mas são exclusivamente devido à eficácia dos nossos protótipos encontrados para os valores “S, S[U,u], S[D,d]”, e um fator adicional de diferenças podem ser erros de simulação, que são mais do que valores maiores de "n, m" que estamos tentando simular, porque somos forçados a limitar a profundidade da simulação em vista da falta do poder de computação dos computadores eletrônicos modernos.

Conclusão

O desenvolvimento desse modelo matemático me levou muito tempo, porque tive que inventar toda a matemática do zero, mas estou feliz com o resultado. Nos próximos artigos tentarei desenvolver vários modelos matemáticos mais universais para que, combinando-os, seja possível calcular qualquer configuração de negociação para suas características principais. Além disso, este modelo matemático é adequado não apenas para descrever processos de precificação, mas também para descrever sinais de negociação e simplificar estratégias complexas, reduzindo-as a outras mais simples. Isso vai levar algum tempo.

Links

Combinatória e teoria da probabilidade para negociação (Parte I): fundamentos

Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/9570

Arquivos anexados |

Baixar como ZIP

Materials.zip (312.85 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Como se tornar um bom programador (Parte 2): mais cinco hábitos que devem ser abandonados para programar melhor em MQL5

Este artigo é uma leitura obrigatória destinada a todos que desejam melhorar sua carreira como programadores. O objetivo desta série de artigos é ajudar o leitor, incluindo experientes, a melhorar suas habilidades de programação. As ideias descritas são aplicáveis tanto a programadores iniciantes em MQL5 quanto a profissionais.

$Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal$ Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal

Neste artigo, continuaremos a estudar fractais e prestaremos muita atenção a resumir todo o material. Tentarei apresentar todos os projetos da maneira mais compacta e compreensível para serem aplicados ao trading.

Como se tornar um bom programador (Parte 3): cinco dicas para programar melhor em MQL5

Perceptron Multicamadas e o Algoritmo Backpropagation (Parte II): Implementação em Python e Integração com MQL5

Um pacote python foi disponibilizado com o proposito de trazer integração com MQL, com isso abre-se as portas para enumeras possibilidades como, exploração de dados, criação e uso de modelos de machine learning. Com essa integração nativa entre MQL5 e Python, abriu-se as portas para muitas possibilidades de uso, podemos construir de uma simples regressão linear a um modelo de aprendizado profundo. Vamos entender como instalar e preparar o ambiente de desenvolvimento e usar algumas das bibliotecas de aprendizado de maquina.