Il modello di regressione di Sultonov (SRM) - che pretende di essere un modello matematico del mercato.
cercare i modelli, descrivere i modelli principali
Tutte le ipotesi di base della teoria della correlazione e della regressione si basano sul presupposto che i dati in studio siano normalmente distribuiti. I vostri input (prezzo) hanno una distribuzione normale?
Tutte le ipotesi di base della teoria della correlazione e della regressione si basano sul presupposto che i dati in studio siano normalmente distribuiti. I vostri input (prezzo) hanno una distribuzione normale?
non l'ha capito
In linea di principio, mostrerò che RMS rileva qualsiasi modello incorporato in una serie di cifre, comprese le serie temporali (RT), credo, indipendentemente dalla natura dell'aspetto di quelle cifre nella serie. Tutte queste e altre sottigliezze saranno discusse usando esempi concreti, inclusa l'analisi di serie casuali.
RMS troverà un modello valido o fittizio, ma a causa della mancanza di normalità della distribuzione il valore predittivo del modello sarà 0. Queste non sono sottigliezze, questo è il fondamento.
Cosa, esattamente, non ha capito?
RMS troverà un modello reale o immaginario, ma a causa della mancanza di normalità della distribuzione, il valore predittivo del modello sarà 0. Questa non è sottigliezza, è la base.
RMS troverà la dipendenza più adeguata, piuttosto che una dipendenza derivata. E sull'assenza o presenza di normalità della distribuzione dei dati iniziali apriamo una discussione separata e lasciamo che gli esperti di questa base parlino qui in parallelo.
Capito..... E giusto - dimentica la normalità! Si mette in mezzo.
P.S. il valore predittivo del modello sarà vicino allo 0
Cominciamo con una funzione lineare.
Immaginiamo che una serie sia data dai numeri Yi = a+bxi:
xi Yi
0,00000001 10,0000
1,00000001 15,0000
2,00000001 20,0000
3,00000001 25,0000
4,00000001 30,0000
5,00000001 35,0000
6,00000001 40,0000
7,00000001 45,0000
8,00000001 50,0000
9,00000001 55,0000
10,00000001 60,0000
11,00000001 65,0000
12,00000001 70,0000
13,00000001 75,0000
14,00000001 80,0000
15,00000001 85,0000
16,00000001 90,0000
17,00000001 95,0000
18,00000001 100,0000
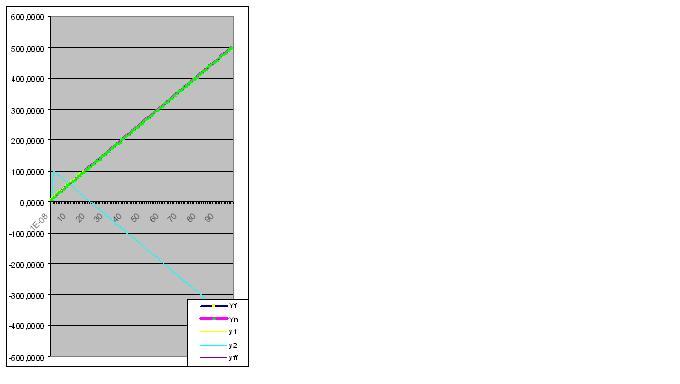
Ecco un grafico dei valori reali e calcolati, l'errore del modello è 2.78163E-14%:
Capito..... E giustamente - al diavolo la normalità! È solo un intralcio.
P.S. il valore predittivo del modello sarà vicino allo 0
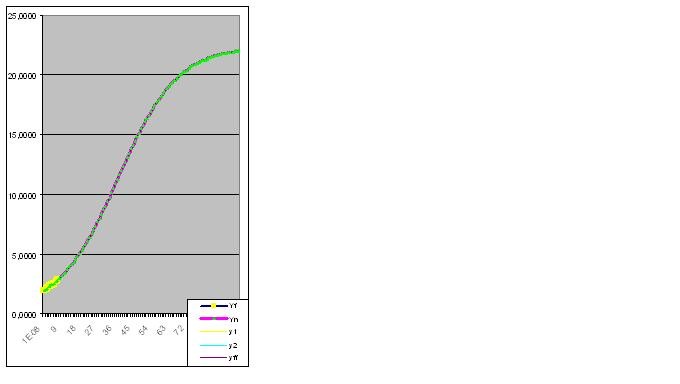
A causa della vostra insistenza, devo iniziare a dimostrare la capacità predittiva del modello analizzando la funzione Y=tg(0,1x)+2 e introducendo le prime 8 coppie di cifre:
xi Yi
0,00000001 2,0000
1,00000001 2,1003
2,00000001 2,2027
3,00000001 2,3093
4,00000001 2,4228
5,00000001 2,5463
6,00000001 2,6841
7,00000001 2,8423
Errore 0,427140953%:
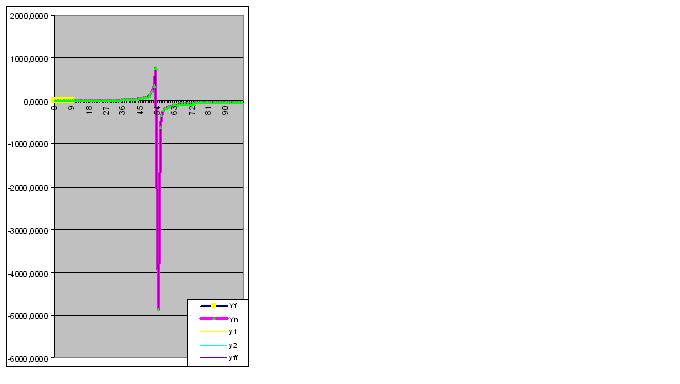
Tuttavia, non appena viene inserita la nona coppia di cifre, il modello predice immediatamente il comportamento "strano" dell'oggetto nel futuro:
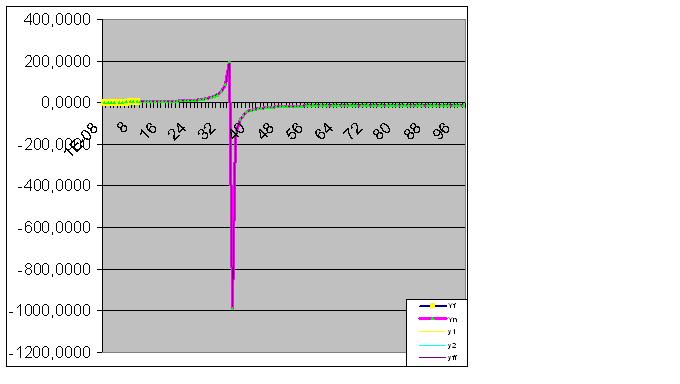
Un ulteriore inserimento di dati avvicina l'"anomalia" prevista ai dati originali:
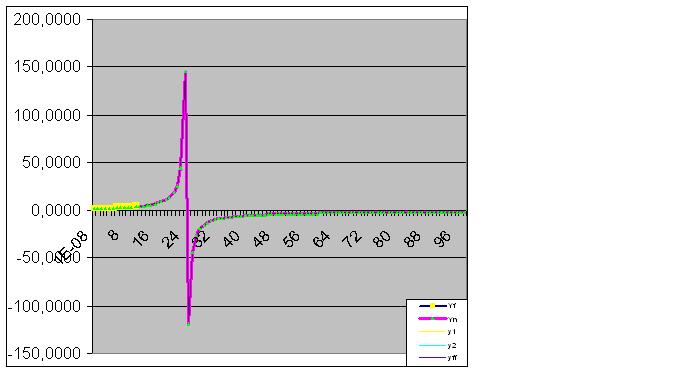
Qui i dati grezzi hanno anche iniziato a eseguire la "finta" prevista:
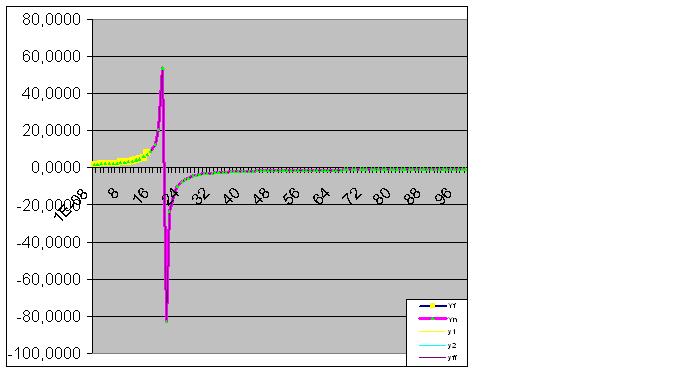
Infine, la predizione è perfettamente realizzata:
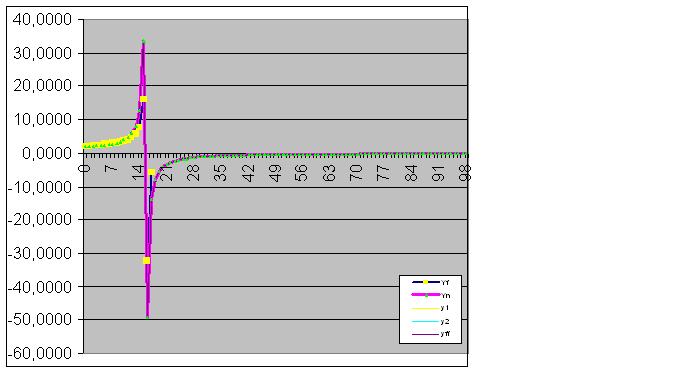
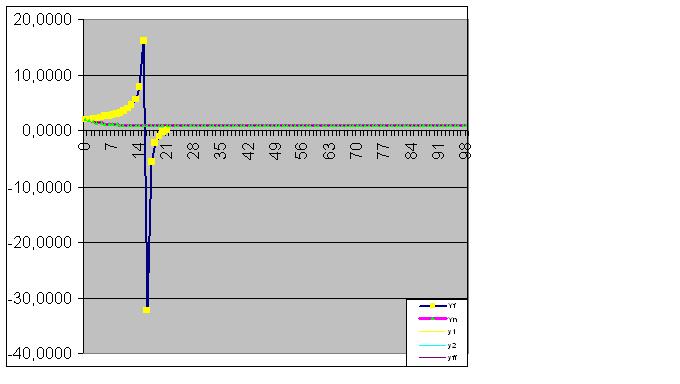
Poi, il modello cattura perfettamente lo stato finale dell'oggetto, in modo che la somma dei valori effettivi della funzione sia uguale all'RMS calcolato con precisione informatica
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Cari membri del forum, non è un segreto che la questione di trovare le dipendenze che descrivono i modelli di base del mercato è importante. Qui cercheremo di affrontare questa questione con tutti i mezzi di analisi disponibili, comprese le varie proposte dei partecipanti su questo tema e il materiale teorico e pratico accumulato in questo momento da tutte le fonti possibili. Come risultato di questo lavoro, se ci soffermiamo anche solo su una visione di questa funzione, penso che considereremo che il tempo e lo sforzo non sono stati spesi invano.
Inizierò dimostrando le capacità di RMS con semplici esempi di descrizioni di modelli noti: lineare, parabola, iperbole, esponente, seno, coseno, tangente, cotangente e altri, così come la loro combinazione, che sono certamente presenti sul mercato. Vi prego di sostenermi in questo impulso con suggerimenti costruttivi e sane critiche, se necessario.