Combinatoria e teoria della probabilità per il trading (Parte I): Le basi

Contenuto

• Introduzione
• In che modo la teoria delle probabilità può essere utile nell'analisi di mercato?
• Specificità della teoria della probabilità applicata al trading manuale e automatico
• Alberi di probabilità e ipotesi
• Informazioni sui frattali
• Schema di Bernoulli
• Creazione del primo frattale
• Riepilogo
• Conclusioni

Introduzione

A mio avviso, il linguaggio della teoria delle probabilità può fornire un livello di comprensione completamente diverso dei processi in atto all'interno del mercato. Dopo aver compreso le specificità della teoria della probabilità, inizierete a pensare in modo completamente nuovo. Idee vaghe o alcuni suggerimenti non provati non causeranno più il desiderio di affrettarsi a fare trading su un conto reale. D'altra parte, capisco che questo nuovo approccio potrebbe non essere comodo per tutti. In questa serie, voglio mostrarvi un approccio reale e corretto al trading. Tutte le decisioni devono basarsi esclusivamente sui numeri, evitando supposizioni come "forse", "e se", "sembra" e simili.

In che modo la teoria delle probabilità può essere utile nell'analisi di mercato?

Mi sono occupato di scienze tecniche per un periodo abbastanza lungo della mia vita, ma la teoria delle probabilità è stata la più difficile per me. Questo perché non comprendevo quanto fossero ampie le sue possibilità. Un vantaggio indiscutibile è rappresentato dalle sue capacità illimitate, che dipendono solo dal vostro ingegno e dalla vostra diligenza, oltre che naturalmente dalla vostra intelligenza. Dopo anni spesi in studi tecnici, mi sono reso conto che l'intelligenza non riguarda la velocità e l'attenzione nell'eseguire gli stessi tipi di operazioni, ma la flessibilità della mente. Se consideriamo, ad esempio, la matematica differenziale, la teoria dei campi vettoriali e scalari, o anche l'algebra scolastica, tutte implicano un certo insieme di regole o raccomandazioni, seguendo le quali è possibile risolvere quasi tutti i problemi. Ogni compito non standard è uno shock per il nostro cervello. Nella teoria della probabilità, esiste un numero infinito di momenti di questo tipo — è qui che molti problemi possono essere risolti solo con approcci completamente differenti. In altre parole, l'intelligenza può essere sviluppata solo attraverso la diligenza e la volontà di risolvere un determinato problema, e la teoria della probabilità può aiutarvi in questo senso.

Il quadro della teoria delle probabilità descrive concetti fondamentali del trading come l'aspettativa matematica, le possibili probabilità di vari eventi, i valori medi, i percentili e altro ancora. La teoria delle probabilità sostiene che non esiste un sistema di trading perfetto e che ogni sistema ha i suoi rischi. Quello che possiamo fare è scegliere solo il sistema di trading i cui rischi non causi troppi disagi. La cosa più importante è interpretare correttamente questi rischi. In altre parole, si passa da un linguaggio impreciso di sensazioni o approssimazioni visive a criteri quantitativi chiari. Naturalmente anche le stime visive sono importanti, ma funzionano meglio se combinate con variabili quantitative. È impossibile descrivere tutti i dettagli e le sfumature in un solo articolo, ma proverò ad includere qui alcune informazioni interessanti. Spero, troviate qualcosa di utile.

Specificità della teoria della probabilità applicata al trading manuale e automatico

Prima di procedere all'utilizzo della teoria delle probabilità per l'analisi del mercato, dobbiamo prima conoscere gli eventi e le loro probabilità. Un evento è un insieme di risultati che soddisfano alcuni criteri o che sono raggruppati secondo un certo criterio in un determinato insieme. Un risultato è un elemento elementare certo che è uguale a ogni altro elemento del gruppo dato. Il gruppo si riferisce a tutti i possibili risultati di un processo. Non è così importante che tipo di processo sia, quale sia la sua fisica o quanto tempo il processo richiede. La cosa importante è che come risultato di questo processo otterremo qualcosa che non esisteva prima del completamento del processo. I risultati che si riferiscono al nostro evento, sono essenzialmente il nostro evento — per comodità, li combiniamo in un unico oggetto. L'idea di cui sopra può essere visualizzata come segue:

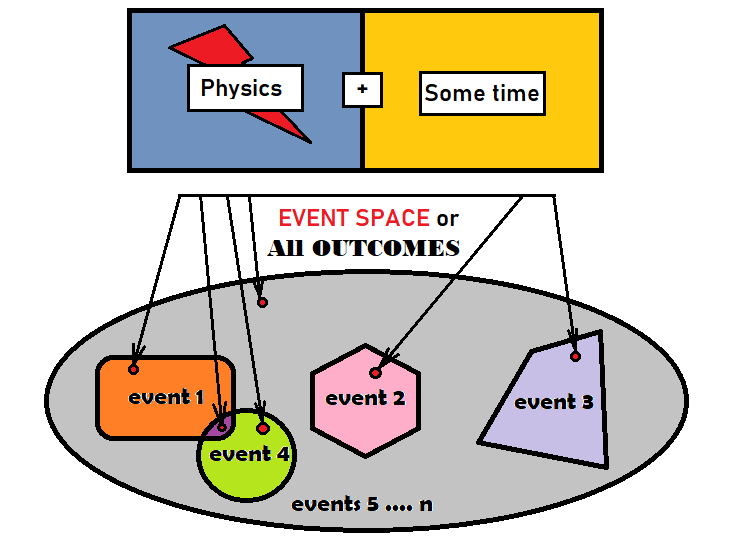
L'ellisse grigia nella figura precedente rappresenta tutti i risultati. In matematica si chiama spazio degli eventi. Questo non significa che lo spazio degli eventi abbia una forma geometrica, ma è abbastanza adatto a descrivere questi concetti. Ci sono 4 eventi all'interno dell'ellisse. Come si può vedere dalla figura, all'interno di ogni evento è presente un piccolo punto rosso. I punti possono essere in numero limitato o illimitato — a seconda del processo in esame. Due degli eventi della figura si intersecano. Tali eventi vengono definiti sovrapposti. Quindi, ci sono alcuni risultati che appartengono a entrambi gli eventi. Tutti gli altri eventi non si sovrappongono, poiché si trovano in parti diverse dell'ellisse e non si intersecano geometricamente. Il resto dell'area grigia può essere considerato l'ultimo evento, oppure può essere suddiviso in parti più piccole fino a quando non rimangono aree grigie.

Ogni evento ha almeno un numero corrispondente, di solito chiamato probabilità. La probabilità indica la frequenza con cui questo evento si manifesterebbe durante le ripetizioni dello stesso processo se potessimo produrre lo stesso esperimento all'infinito. Esistono due tipi di spazi per eventi:

1. Con un numero finito di esiti possibili
2. Con un numero infinito di risultati possibili

Se il numero di esiti è finito, la probabilità può essere calcolata come segue:

• P = S/N , S è il numero di esiti che soddisfano il criterio dell'evento, N è il numero totale di tutti gli esiti nello spazio degli eventi

In alcuni casi, quando il numero di esiti in un certo spazio è infinito, questa probabilità può anche essere determinata, ad esempio utilizzando gli integrali. Nel caso dell'immagine precedente, i valori "S" e "N" possono essere sostituiti dalle aree delle loro forme geometriche.

Non è sempre possibile definire chiaramente quale sia lo spazio dell'evento, così come definire il numero di risultati e la fisica descritta dagli eventi. Queste rappresentazioni grafiche hanno solo lo scopo di aiutare a disegnare analogie per il nostro cervello, in modo che non funzioni più con una certa geometria e non cerchi di capire cosa e perché, ma si abitua all'idea che lavoriamo esclusivamente con probabilità e numeri extra, che corrispondono a queste possibilità. Gli eventi possono anche essere chiamati stati. Se usiamo la logica degli stati, allora la probabilità è esattamente la frequenza di comparsa di uno stato specifico come risultato della ripetizione degli stessi esperimenti. 

Per analogia con le aree delle figure, la somma delle aree di tutte le figure incluse nell'ellisse è esattamente uguale all'area di questa ellisse. In termini matematici, l'area è il numero di risultati che vi rientrano. Quindi:

• N = S[1] + S[2] + ... + S[n]
  
• S è il numero di esiti di un particolare evento
• N è l'insieme dei risultati dello spazio degli eventi

Dividendo entrambi i lati dell'uguaglianza per il valore N, si ottiene una relazione interessante e molto importante che è alla base dell'intera teoria della probabilità:

• 1 = S[1]/N + S[2]/N + ... +S[n]/N

Notare che questo rapporto funziona solo per eventi non sovrapposti. Perché se gli eventi sono congiunti, le aree delle forme si sovrappongono e la somma delle loro aree sarà maggiore dell'area dell'ellisse originale. È simile a un puzzle, in cui l'area di tutti i pezzi del puzzle è esattamente uguale all'immagine risultante. In questo caso, un pezzo del puzzle rappresenta uno degli eventi. Tutte queste frazioni rappresentano le probabilità di eventi specifici:

• 1 = P[1] + P[2] + ... +P[n]

Questo rapporto come base del termine insieme di eventi collettivamente esaustivo. Un insieme di eventi collettivamente esaustivo è l'unità di tutti gli eventi non sovrapposti che formano un certo spazio di eventi. Per un puzzle, un insieme collettivamente esaustivo è costituito da tutti i pezzi del puzzle. La probabilità totale di tutti questi eventi deve essere uguale a uno, il che significa che uno di questi eventi deve necessariamente verificarsi come risultato dell'esperimento. Non sappiamo quale evento si verificherà, ma lo scopriremo dal risultato dell'esperimento.

In base a quanto sopra, qualsiasi insieme di risultati dello spazio eventi selezionato può essere considerato un evento. Ciò significa che un insieme collettivamente esaustivo può essere raccolto in tutti i modi e le combinazioni possibili. Quando operiamo con un numero finito di risultati, può esistere un numero limitato di combinazioni di questo tipo; per un numero infinito di risultati, il numero di combinazioni sarà sempre infinito. Se è noto che il numero di esiti è pari all'infinito, i matematici considerano il concetto di valore casuale. In alcuni casi, i valori casuali possono essere più convenienti da utilizzare, poiché ciò è consentito dal compito. Un valore casuale è un metodo un po' diverso per descrivere lo spazio degli eventi. In questo caso il risultato è l'insieme chiaro di uno o più numeri. Possiamo dire che si tratta di un vettore. Questo modello di considerazione implica il concetto di densità di probabilità. 

Penso che valga la pena almeno di dare un'occhiata superficiale a questi concetti, perché ne avremo bisogno in futuro quando considereremo il resto del materiale e per una certa comprensione da parte nostra. La densità di probabilità è una funzione che descrive l'intero spazio degli eventi. La dimensione di questa funzione è esattamente uguale al numero dei numeri necessari per descrivere ogni risultato in questo spazio degli eventi. Ad esempio, se consideriamo il problema di sparare a un bersaglio in un poligono di tiro, la dimensione di questa funzione sarà pari a due, perché il bersaglio è piatto (bidimensionale). In questo caso, un particolare risultato sarà caratterizzato dalle coordinate X e Y. Questi numeri sono le nostre variabili casuali, quindi possiamo scrivere quanto segue:

• R = R(X,Y)
• R è la densità di probabilità che un proiettile colpisca un punto con coordinate (X,Y)

Le proprietà di questa funzione fanno sì che l'integrale completo da meno a più infinito per tutte le variabili di questa funzione sia uguale a uno, il che dimostra l'equazione sopra. Le probabilità sono determinate solo dagli integrali dell'area in cui è presentata la funzione. I diversi eventi possono essere composti da regioni integrate in modo frammentario. Quindi, è possibile descrivere tutti gli eventi di cui abbiamo bisogno, perché il loro numero è infinito. Questa definizione è sufficiente nell'ambito di questo articolo.

Vorrei aggiungere altri dettagli sulla sovrapposizione degli eventi. Questi eventi sono molto importanti anche per la comprensione del quadro generale nel suo complesso. È chiaro che gli eventi non sovrapposti dovrebbero essere più facili da gestire rispetto a quelli sovrapposti. La teoria della probabilità a volte ha a che fare con la combinazione o la divisione di eventi. Ma qui siamo interessati solo alle probabilità che appaiono come risultato di queste trasformazioni. A questo scopo, utilizzeremo i concetti di somma e prodotto di eventi come l'operazione di inversione. Queste operazioni non hanno lo stesso significato come in matematica. Inoltre, operano solo con le probabilità. Le probabilità di eventi congiunti non possono essere sommate, perché ciò violerebbe l'integrità dell'insieme. In generale, queste 3 operazioni applicate agli eventi sorgente possono descrivere tutti i possibili eventi che possono essere composti da pezzi di eventi sorgente. Utilizzando l'esempio di due eventi sovrapposti, posso mostrare come può apparire sul piano:

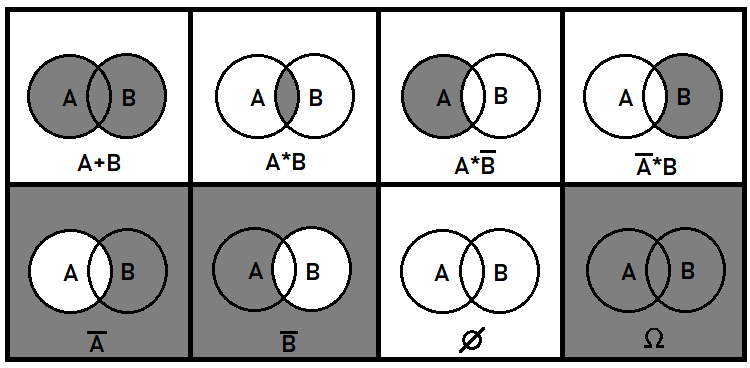
Ulteriori operazioni algebriche possono essere composte da quelle presentate sopra. Ad esempio, la divisione Booleana è equivalente alla terza e alla quarta situazione della figura precedente, poiché la divisione è equivalente alla moltiplicazione per l'inverso dell'evento selezionato. Tecnicamente, i primi due eventi sono sufficienti per descrivere tutti i possibili eventi che possono essere composti da parti di eventi sorgente. I casi con più di due eventi sovrapposti sono molto più difficili. In questo articolo ci occuperemo solo di eventi non sovrapposti.

La matematica dei mercati si basa principalmente sul concetto di passeggiata casuale. Prenderemo in considerazione questo concetto e poi sarà possibile generalizzare questi eventi in base alla presenza di modelli (pattern). Supponiamo di aprire una posizione con stop loss e take profit equamente distanziati dai prezzi di apertura. In questa sede non consideriamo gli spread, le commissioni e gli swap. Quindi, se apriamo una posizione di trading liberamente e facciamo trading a caso in diverse direzioni e in diversi punti del grafico, il rapporto tra profitto e perdita sarà pari a uno. In altre parole, il numero di posizioni redditizie sarà uguale al numero di posizioni perdenti nel trading infinito. In base a quanto detto sopra, il profitto sarebbe pari a zero indipendentemente dalla durata del trading. Se si applicano tutte le commissioni, gli spread e gli swap, il risultato finale sarà negativo.

La camminata casuale può sembrare priva di significato, poiché la matematica di questo processo porta sempre a delle perdite. Ma la camminata casuale può aiutare a calcolare le probabilità di diversi eventi. Questi possono includere la chiusura con stop asimmetrici o il prezzo medio che il grafico supererà in un determinato intervallo di prezzi. Possiamo anche calcolare la durata della posizione e altre variabili utili che possono aiutare a calcolare i rischi o a cercare di massimizzare i profitti o minimizzare le perdite.

Alberi di probabilità e ipotesi

Un esempio molto utile per sviluppare i lobi frontali sono gli alberi degli eventi, o alberi delle probabilità. Questo argomento trae origine dallo schema di Bernoulli, che è alla base di tutti gli alberi delle probabilità. Questo schema esamina le catene di eventi non sovrapposti che si susseguono. Ma prima di ciò, consideriamo la formula della probabilità totale. Studiando questa importante costruzione, possiamo procedere allo schema di Bernoulli e quindi agli alberi di probabilità. La formula si presenta così:

• P(A) = Sum(0 ... i .... n) [ P(H[i]) * P(A|H[i]) ] — probabilità dell'evento A
• P(H[i]) — probabilità dell'ipotesi H[i]
  
• P(A|H[i]) — probabilità che l'evento A si verifichi nell'ambito dell'ipotesi H[i]

Vorrei dire che quando si lavora con le probabilità, è meglio scriverle nello stile delle ipotesi. Ad esempio, la voce P(H[k]|H[i]) significa quanto segue:

1. La probabilità dell'evento H[k] calcolata rispetto allo spazio H[i]

In questo modo è chiaro quale evento è considerato spazio e quale evento è annidato. Il fatto è che ogni evento è uno spazio per eventi più piccolo, all'interno del quale possono esserci altri eventi, che possono servire anche come spazi per eventi, e così via. Secondo questa logica, la voce P(H[i]) può essere scritta come segue:

• P(H[i]|O) — poiché questa probabilità è stimata rispetto a O.
  

Dividiamo ora la formula della probabilità totale in parti per capire cosa c'è dietro. La formula può sembrare difficile a prima vista, quindi cerchiamo di renderla più chiara. Per prima cosa, riscriverò la formula in maniera leggermente diversa:

• P(A) = (S[0] + ... + S[i] + ... + S[n]) / O   =   S[0]/O + ... + S[i]/O + ... + S[n]/O  =  (S[0]/N[0]) * ( N[0]/O ) + ... + (S[i]/N[i]) * ( N[i]/O ) + ... + (S[n]/N[n]) * ( N[n]/O )
• S[i] — l'area del segmento specifico di intersezione dell'ipotesi H[i]
• N[i] — l'area dell'intera ipotesi H[i] (compresa S[i])
• O — tutti gli esiti o l'area dell'intera ellisse

Dopo piccole trasformazioni, che consistono nel moltiplicare il numeratore e il denominatore per il valore N[i], possiamo vedere le probabilità presenti nella formula originale:

• S[i]/N[i] ----> P(A|H[i])
• N[i]/O ----> P(H[i])

Può essere visualizzato graficamente come segue:

 

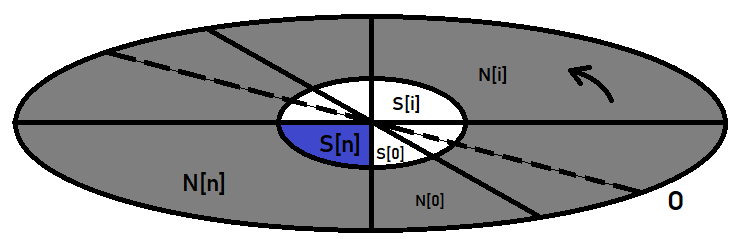
L'ellisse esterna è lo spazio degli eventi. L'ellisse centrale rappresenta il nostro evento, di cui stiamo cercando la probabilità. Supponiamo che sia un orologio: disegnate il diametro dell'ellisse, ruotatelo in senso antiorario e tagliate l'ellisse in segmenti che sono ipotesi. Un'ipotesi è solo un nome speciale per gli eventi. Tuttavia, in realtà si tratta degli stessi eventi, non diversi da quello per cui stiamo calcolando la probabilità.

Questa formula ha un caso particolare, che ci aiuterà a costruire lo schema di Bernoulli. Immaginiamo che l'ellisse centrale sia interamente all’interno di una di queste ipotesi. Si scopre poi che tutti i termini di questa somma, che si riferiscono al resto delle ipotesi, si azzerano automaticamente, perché la probabilità del verificarsi dell'evento A all'interno di queste ipotesi è impossibile o uguale a zero, il che finisce per azzerare questi termini. Di conseguenza, risulta che:

• P(A) = P(H) * P(A|H)
• H — la probabilità dell'ipotesi, all'interno della quale si trova l'evento selezionato.

Inoltre, cosa succede se assumiamo che anche l'evento A sia chiamato ipotesi? Perché no? Un'ipotesi è un evento, quindi qualsiasi evento è un'ipotesi. Supponiamo ora che esista un altro evento B, che si trova all'interno di A. Allora A è un'ipotesi relativa a B e la formula precedente è applicabile a questi due eventi:

• P(B) = P(A) * P(B|A) = P(H) *  P(A|H) *  P(B|A)

Inserendo il rapporto precedente al posto di P(A) — si può notare un certo schema nella costruzione di una formula generale per qualsiasi numero di ipotesi o eventi annidati. Qual è il suo scopo? Questo è il prototipo diretto della formula di Bernoulli, che considereremo tra poco. Ora, c'è un altro fatto interessante da considerare.

Informazioni sui frattali

In accordo con la formula precedente, se P(A) + P(B) = 1, si tratta di un insieme collettivamente esaustivo di eventi. Ciò significa che un gruppo completo può essere composto da due catene arbitrarie di ipotesi che sono annidate l'una nell'altra. Ma queste ipotesi possono essere sovrapposte. Se richiediamo che tutte le possibili ipotesi annidate non si sovrappongano alle ipotesi di altre catene, allora automaticamente tutte le catene saranno non sovrapposte a tutte le catene in questo spazio di eventi. Una rappresentazione grafica di questo modello è piuttosto interessante:

Questo modello è chiamato Frattale, perché una struttura così non può essere costruita fino alla fine, ma può essere costruita all'infinito. Nella figura sopra, la struttura è profonda solo 3 livelli. I rettangoli blu rappresentano la fine di una catena separata di probabilità. Se sommiamo le probabilità di tutte queste catene, esse formeranno un insieme collettivo esaustivo di eventi.

Tali frattali possono essere ben descritti da combinazioni. Le combinazioni si basano sul concetto di fattoriale. Esiste un altro concetto, la permutazione, che si colloca a metà strada tra il fattoriale e la combinazione. La formula di permutazione deriva dalla formula fattoriale e il concetto di combinazione deriva dalla formula di permutazione. Ecco le formule corrispondenti:

• n! - fattoriale del numero n
• P(n,k) = n! / ( n - k )! — permutazioni di N elementi per K elementi
• С(n,k) = n! / ( k! * ( n - k )! ) — combinazioni di N elementi per K elementi

Un fattoriale è il prodotto di tutti i numeri naturali che iniziano con 1 e terminano con n, mentre "0! = 1". Cioè, il fattoriale di zero è uguale a uno. In questo caso si tratta solo di un'eccezione alla regola, ma non ho visto un singolo caso in cui questa eccezione possa interferire con i calcoli o complicare gli algoritmi.

Le permutazioni sono un po' più complicate. Immaginate di avere un mazzo di carte e che questo mazzo abbia un certo numero di carte. Conducete un semplice esperimento: mescolate il mazzo e prendete alcune carte dal mazzo in modo del tutto casuale, mettetele sul tavolo nell'ordine in cui sono state estratte dal mazzo. Quindi, le permutazioni sono il numero di tutti i possibili risultati di questo esperimento, mentre l'ordine delle carte è anche considerato un identificatore unico di un particolare risultato. Tale permutazione è applicabile a qualsiasi elemento desiderato.

La prima carta può essere presa dal mazzo in n modi diversi, la seconda può essere presa in "n-1" modi, dato che la prima carta non è più nel mazzo. E così via, fino alla carta "n-k-1". Per ottenere il numero di tutte le permutazioni possibili, dobbiamo moltiplicare tutti i numeri da "n-k-1" a "n". Questa procedura assomiglia a un fattoriale. Se prendiamo "n!" e lo dividiamo per "n-k" fattori, otterremo il prodotto originale che è esattamente uguale a "(n-k)!". In questo modo si ottiene la formula di permutazione.

La formula di combinazione è un po' più complicata, ma è anche molto facile da dedurre. Abbiamo tutte le possibili permutazioni, ma l'ordine degli elementi non importa — contano solo le carte di questo set. Ora dobbiamo trovare il numero di questi casi, ognuno dei quali ha una serie differente di carte. In realtà, ogni permutazione contiene già uno di questi insiemi unici, ma non ci servono tutti. Cambiamo la logica e proviamo a raccogliere tutte le permutazioni di tutte le combinazioni possibili: si scopre che se prendiamo una combinazione, non importa come riorganizziamo gli elementi in essa contenuti, essi saranno unici. Inoltre, se prendiamo tutte le combinazioni uniche e produciamo tutte le possibili permutazioni al loro interno, otteniamo quanto segue:

• P(n,k) = C(n,k) * P(k,k)

Il numero di tutte le possibili permutazioni uniche all'interno di una combinazione è pari a "P(k,k)", perché dobbiamo raccogliere da "k" varianti tutte le possibili permutazioni per queste "k" varianti. Dividendo entrambe le parti dell'equazione per "P(k,k)", si ottiene la formula di combinazione richiesta:

• C(n,k) = P(n,k)/P(k,k) = n! / ( k! * ( n - k )! )
  

Sia le permutazioni che le combinazioni sono ampiamente utilizzate per i vari problemi di teoria della probabilità. Quando si tratta di applicazioni pratiche, sono le combinazioni ad essere estremamente utili. Le combinazioni sono utilizzate nella costruzione di funzioni frattali per diversi scopi. Forse sarebbe più corretto chiamarle ricorrenti, ma per qualche motivo chiamo queste funzioni frattali (probabilmente perché sono davvero frattali, quindi non si tratta solo di un processo ricorsivo ma di un intero albero di chiamate).

Schema di Bernoulli

Prima di procedere allo studio di tali funzioni frattali, consideriamo la nota formula di Bernoulli. Supponiamo di avere una catena di esperimenti identici che dobbiamo ripetere diverse volte. L'esperimento deve portare alla comparsa o meno di un evento con una certa probabilità. Inoltre, supponiamo di voler trovare la probabilità che in una catena di "n" esperimenti il nostro evento apparirà esattamente "k" volte. La formula di Bernoulli può rispondere a questa domanda:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k) — Formula di Bernoulli
  
• p — la probabilità di occorrenza dell'evento come risultato di un singolo esperimento
• q = 1 - p — la probabilità che l'evento non si verifichi come risultato dell'esperimento

Ricordate la formula derivata in precedenza per le catene probabilistiche? Estendiamola per una catena di lunghezza arbitraria:

• P(n) = P(H[1]|O) *  P(H[2]|H[1]) *  P(H[3]|H[2]) * ... * P(H[k]|H[k-1]) * ... *P(H[n]|H[n-1])
• n — il numero di segmenti della catena
• O — l'insieme dei risultati; può essere indicato come H[0]

Questa formula calcola la probabilità che si verifichi la catena di ipotesi esattamente richiesta. La formula può essere rappresentata visivamente come segue:

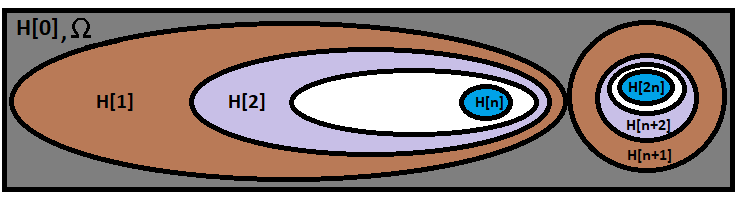
La nostra formula si trova nella prima e più grande ellisse, mentre un'altra catena sulla destra non si sovrappone alla nostra e simboleggia un altro ramo di una combinazione diversa. Esistono esattamente tanti rami di questo tipo quante sono le varianti per il calcolo delle combinazioni nella nostra formula. Non confondete quindi le combinazioni con le varianti di calcolo delle combinazioni. Il numero delle varianti per il calcolo delle combinazioni è pari a:

• n+1 (perché vengono conteggiate anche le combinazioni di esiti positivi "0")
• n è il numero di test indipendenti nella catena degli esperimenti

Immaginiamo ora che le probabilità di tutte queste ipotesi siano uguali a "p" o "q". La formula viene quindi semplificata:

• P(n) = Pow(p,k)*Pow(q,n-k)
• k — quanti fattori uguali a "p" ci sono nel prodotto
• n-k — quanti fattori uguali a "q" ci sono nel prodotto

Assomiglia già alla formula di Bernoulli, ma manca la combinazione. Se si riflette attentamente, diventa chiaro che le varianti delle catene con una probabilità simile e la quantità di "k" e "n-k" è esattamente uguale a "C(n,k)". Poiché tutte le catene di probabilità non si sovrappongono, la probabilità di ottenere una di queste catene è la somma delle probabilità di tutte le catene. Poiché tutte queste probabilità sono uguali, possiamo moltiplicare la probabilità di una catena per il loro numero per ottenere la formula di Bernoulli:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)

Questa formula può essere ulteriormente ampliata, ad esempio, quando è necessario trovare la probabilità di una combinazione non strettamente fissa, ma di un evento che si verifica k e più volte, k e meno volte e tutte le combinazioni simili. In questo caso, sarà la somma delle probabilità di tutte le combinazioni richieste. Ad esempio, la probabilità che l'evento si verifichi più di k volte è calcolata come segue:

• P = Summ(k+1 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i)]

È importante capire che:

• P = Summ(0 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i) ] = 1

in altre parole, tutte le catene possibili formano un insieme di eventi collettivamente esaustivo. Un'altra equazione importante è:

• Summ(0 ... i ... n)[C(n,i)] = Pow(2,n)
  

È logico, dato che ogni segmento della catena di probabilità ha solo due stati: "l'evento si è verificato" e "l'evento non si è verificato". Anche lo stato in cui l'evento non si è verificato è un evento, il che implica che un altro evento è accaduto.

Le combinazioni hanno un'altra interessante proprietà:

• C(n,k) = C(n,n-k)
  

È derivato come segue: calcolare "C(n,n-k)" e confrontarlo con "C(n,k)". Dopo alcune piccole trasformazioni, possiamo vedere che entrambe le espressioni sono identiche. Ho creato un piccolo programma basato su MathCad 15 per verificare tutte le affermazioni di cui sopra: 

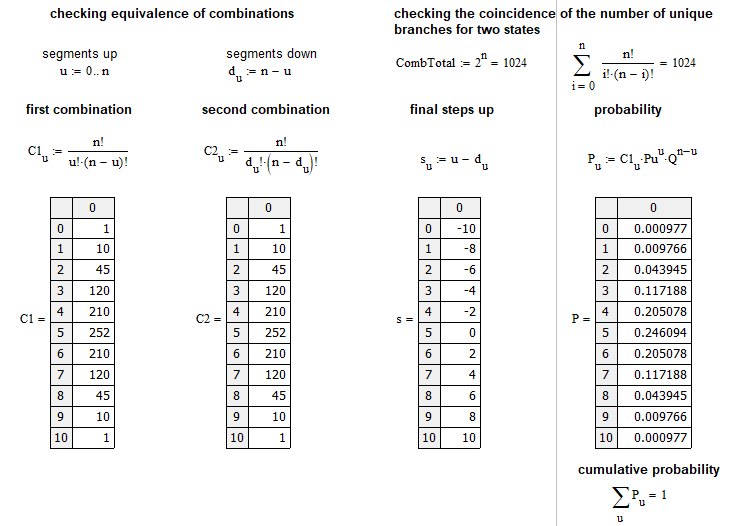
Questo esempio è vicino al mercato. Calcola la probabilità che su n passi il mercato si muova al rialzo di u passi. Un passo è il movimento del prezzo a un certo numero di punti in alto o in basso, rispetto al passo precedente. La matrice grafica delle probabilità per ogni "u" può essere rappresentata come segue:

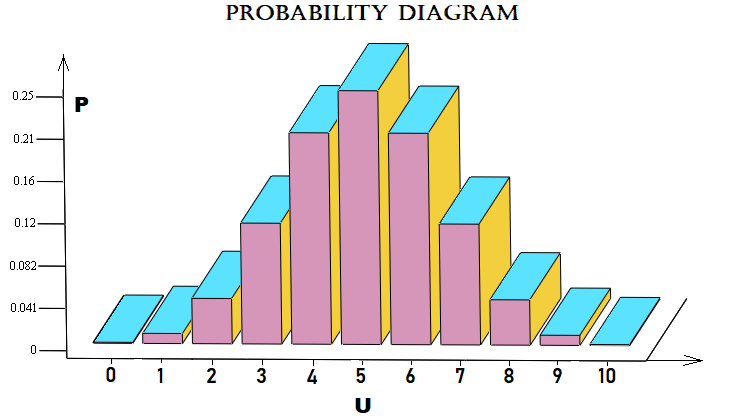
Per semplicità, ho utilizzato uno schema di Bernoulli con 10 passi. Il file è allegato di seguito, in modo da poterlo testare. Non è necessario applicare obbligatoriamente questo schema ai prezzi. Può essere applicato anche agli ordini o a qualsiasi altra cosa.

Creazione del primo frattale

Occorre prestare particolare attenzione ai problemi legati ai livelli di stop loss e take profit. Dovremmo in qualche modo calcolare la probabilità che un'operazione venga chiusa dallo stop loss o dal take profit quando conosciamo i valori dello stop loss e del take profit in punti (distanza dal prezzo corrente). Questo valore può essere calcolato in qualsiasi momento, anche se non è più il prezzo di apertura, poiché tutti questi aspetti dipendono direttamente dai meccanismi di determinazione del prezzo. In questo esempio, voglio dare prova della formula utilizzando i frattali. Nel caso di una passeggiata casuale, questa probabilità può essere calcolata come segue:

• P(TP) = SL / ( TP + SL ) - la probabilità di raggiungere il take profit
• P(SL) = TP / ( TP + SL ) - la probabilità di colpire lo stop loss
• SL — distanza dal punto di stop loss
  
• TP — distanza dal punto di take profit

Queste due probabilità formano un insieme di eventi collettivamente esaustivo:

• P(TP) + P(SL) = 1
  

Secondo questa formula, per il trading casuale, l'aspettativa matematica di tali strategie sarà pari a zero, se si escludono spread, commissioni e swap:

• M = P(TP) * TP - P(SL) * SL = 0

Questo è il caso più semplice quando si imposta un livello di stop fisso. Ma è assolutamente possibile generalizzarla a qualsiasi strategia. Ora dimostriamo la formula utilizzando lo stesso MathCad 15. Lavoro con questo programma da molto tempo. Può produrre calcoli di quasi tutti i livelli di complessità, anche utilizzando la programmazione. In questo esempio, oltre a dimostrare le formule precedenti, vedremo il primo esempio di costruzione di una formula frattale. Iniziamo a delineare il processo di movimento dei prezzi. In questo caso non possiamo utilizzare funzioni continue, ma solo discrete. A tal fine, prendiamo il nostro ordine condizionato e calcoliamo le distanze dei livelli di stop verso l'alto e verso il basso, dopodiché dividiamo questi segmenti in parti con passi uguali, in modo che ogni passo includa un numero intero di passi. Immaginiamo che il prezzo si muova attraverso questi passi. Poiché i passi sono uguali, la probabilità di un passo in una delle due direzioni è pari a 0,5. Abbiamo bisogno di una rappresentazione grafica per implementare il frattale appropriato:

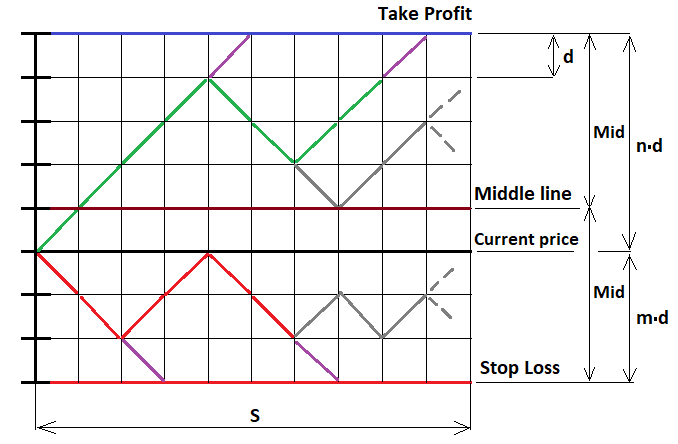
Per risolvere questo problema, consideriamo tre possibili casi di continuazione frattale:

1. Siamo al di sopra della linea mediana ( U > MiddleLine )
2. Siamo al di sotto della linea mediana ( U < MiddleLine )
3. Siamo al livello della linea mediana ( U = MiddleLine )

"U" è il numero totale di passi "u-d" verso l'alto rispetto al prezzo di apertura. Se il punto da cui si intende continuare a costruire il frattale è al di sotto del prezzo, allora U assume valori negativi in base alla funzione. Se ci troviamo sulla linea di mezzo, il numero di passi che possiamo fare senza temere di superare la linea è uno in meno rispetto a Mid. Ma prima di procedere con la costruzione, dobbiamo limitare la costruzione frattale al numero di passi che il prezzo o gli ordini possono fare. Se il numero di passi supera il numero richiesto, dobbiamo interrompere la sua costruzione. In caso contrario, si otterrà una ricorsione infinita, dalla quale sarà impossibile uscire. Il suo tempo di calcolo sarà pari a infinito.

Nella figura, ho disegnato diversi passaggi in viola — in questi punti raccogliamo le probabilità e le sommiamo in una variabile comune. Dopodiché dobbiamo girare la nostra catena verso l'alto o verso il basso, a seconda del confine toccato dalla catena, in modo che possa continuare a muoversi per costruire nuovi livelli frattali annidati. In altri punti, possiamo costruire liberamente livelli frattali completi basati sullo schema di Bernoulli.

Quando è possibile creare un albero basato sullo schema di Bernoulli, dobbiamo prima determinare il numero di passi che possiamo fare, prendendo in considerazione i casi estremi, quando tutti i passi sono solo verso l'alto o solo verso il basso. Per tutti e tre i casi il valore è pari a:

• (n - 1) - U — quando la nostra catena è già al di sopra della linea mediana (poiché un aumento di U provoca una diminuzione della distanza dal limite superiore)
• (m - 1) + U — quando la nostra catena è già al di sotto della linea mediana (poiché una diminuzione di U causa una diminuzione della distanza dal limite inferiore)
• (floor(Mid)-1) — quando la nostra catena si trova esattamente sulla linea mediana
• n — il numero di segmenti superiori
• m — il numero di segmenti inferiori
• floor — la funzione scarta la parte frazionaria (potrebbe non essere necessario)

Per prima cosa dobbiamo calcolare due valori ausiliari:

• Mid = (m+n)/2 — metà della larghezza dell'intervallo (in passi)
• Middle = (m+n)/2 - m — il valore "U" per la linea centrale (in passi)

Questi valori saranno utilizzati in seguito per descrivere la logica di ramificazione frattale. Per ora, creeremo il frattale solo per i casi in cui "n>=m". Tuttavia, questi dati non sono sufficienti per costruire un frattale. Per poter costruire livelli frattali più profondi, è necessario ridefinire "U" per ogni nuova combinazione dello schema di Bernoulli e passarla a un nuovo livello frattale. Inoltre, è necessario incrementare correttamente il numero di passi eseguiti e anche passarli correttamente al livello successivo. Allo stesso modo, dobbiamo raccogliere la probabilità dell'intera catena utilizzando i moltiplicatori del livello frattale successivo e passare la probabilità della catena intermedia al livello successivo, finché il processo non termina con il superamento del confine richiesto. L'immagine seguente spiega queste tre varianti:

  

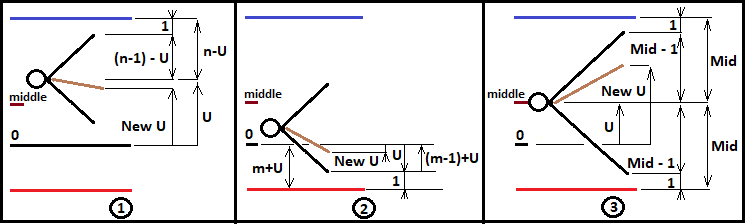
In base a questo diagramma, possiamo ora scrivere a quali valori "NewU" e altri valori ausiliari saranno pari per ogni caso presentato. Consideriamo un esempio di costruzione di un frattale per calcolare la probabilità di attraversamento del limite superiore:

Per il caso 1:

Osserviamo l'immagine superiore e descriviamo matematicamente ciò che sta accadendo. Questa figura mostra un estratto del mio programma in MathCad 15. Il codice completo del programma è allegato di seguito. Qui fornisco i dettagli più importanti che sono alla base del frattale. Il primo rettangolo si trova in un ciclo, che esegue un'iterazione in base a "i" per descrivere tutte le combinazioni possibili. Questa logica può essere ripetuta nell'IDE MetaEditor. Cominciamo con la prima illustrazione del diagramma. Per definire "NewU", dobbiamo prima definire alcune formule fondamentali:

• ( n - 1 ) - U = f — è il numero di passi dell'albero delle combinazioni future (la distanza è determinata dalla distanza dal confine più vicino dell'intervallo frattale)
• u + d = f — lo stesso valore, ma espresso in termini di numero di segmenti ascendenti e discendenti
• s = u - d — il numero di passi finali, espresso in termini di segmenti discendenti e ascendenti
• u = i — questo perché il mio programma usa l'iterazione per "i" (dovrebbe essere ricordato)

Per calcolare tutti i valori richiesti, dobbiamo esprimere "s" attraverso "U" e "i". A tal fine, è necessario escludere la variabile "d". Prima esprimetelo e poi sostituitelo nell'espressione per "s":

1. d = f - u = f - i = ( n - 1 ) - U - i
2. s = i -( n - 1 ) + U + i = -( n - 1 ) + 2*i + U

Quindi, utilizzando la "s" trovata, trovare "NewU" e tutti i valori da passare al livello frattale successivo:

• NewU = s + U = -( n - 1 ) + 2*i + 2*U — la nostra nuova "U" da passare al livello frattale successivo
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( n - 1 ) - U ,i) * Pow(p,i) * Pow(1-p,( n - 1 ) - U -i) — la nostra nuova probabilità della catena "P" di essere passata al livello frattale successivo (ottenuta moltiplicando per la probabilità del nuovo segmento della catena)
• NewS = S + f = S + ( n - 1 ) - U — nuovo "S" da passare al livello frattale successivo

Osservate ora il rettangolo inferiore. Qui gestiamo i casi in cui la catena di passi ha raggiunto il limite superiore dell'intervallo. Due casi dovrebbero essere gestiti qui:

1. Raccolta della probabilità della catena che si interseca con il bordo (sottolineata in rosso)
2. Azioni simili, incrementando nuovi valori che passeremo al livello frattale successivo

Questo caso è molto semplice, poiché esistono solo due varianti possibili:

1. Toccare il confine
2. Ritorno dal confine

Queste azioni non necessitano dello schema di Bernoulli, poiché ogni caso implica un solo passo. La probabilità di inversione viene inoltre moltiplicata per "(1-p)", perché la probabilità di intersezione è "p" e questi due eventi dovrebbero formare un insieme collettivamente esaustivo, come risulta dai calcoli precedenti. I passi vengono incrementati di 1 e "U" viene diminuito di "1", perché si tratta di una riflessione che va verso il basso. Ora abbiamo tutto ciò che serve per costruire correttamente questo caso. Queste regole saranno identiche per la costruzione dei frattali principali, che ci servono per casi completamente diversi.

Per il caso 2:

Il calcolo è quasi simile per questo caso. L'unica differenza è che "f" assume un valore diverso:

• ( m - 1 ) + U = f

Anche in questo caso, esprimere "s" attraverso "U" e "i", utilizzando le stesse formule del caso precedente:

1. d = f - u = f - i = ( m - 1 ) + U - i
2. s = i -( m - 1 ) - U + i = -( m - 1 ) + 2*i - U

Allo stesso modo, trovare tutti gli altri valori che dobbiamo passare al livello frattale successivo:

• NewU = s + U = - ( m - 1 ) + 2*i - nuova "U" da passare al livello frattale successivo
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( m - 1 ) + U ,i) * Pow(p,i) * Pow(1-p,( m - 1 ) + U -i) — la nostra nuova probabilità per la catena "P" di essere passata al livello frattale successivo
• NewS = S + f = S + ( m - 1 ) + U — la nostra nuova "S" da passare al livello frattale successivo

Il rettangolo inferiore è quasi identico al caso precedente, tranne per il fatto che incrementiamo "U" di 1, perché la riflessione sale e quindi "U" aumenta. Le probabilità non vengono raccolte in questo caso, perché non siamo interessati all'intersezione con il bordo inferiore in questo frattale. Ecco l'ultimo caso, quando la catena si è verificata sulla linea centrale dell'intervallo.

Per il caso 3:

Definire "f":

• floor(Mid) - 1 = f

Trovare "s":

1. d = f - i = floor(Mid) - 1 - i
2. s = i - d = -(floor(Mid) - 1) + 2*i

Infine, trovare i valori da passare al livello frattale successivo:

• NewU = s + U = -(floor(Mid) - 1) + 2*i + U
  
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( floor(Mid) - 1,i) * Pow(p,i) * Pow(1-p,floor(Mid) - 1 - i) — la nostra nuova catena di probabilità "P" da passare al livello frattale successivo
• NewS = S + f = S +(floor(Mid) - 1) — il nostro nuovo "S" da passare al livello frattale successivo

Una caratteristica distintiva di questo caso è che il blocco non raccoglie le probabilità, perché le probabilità possono essere raccolte solo ai valori di confine di "U", dove le catene di probabilità vengono anche riflesse nella catena in modo che possano diffondersi ulteriormente. La creazione di un frattale per calcolare la probabilità di attraversare il confine superiore sarà identica, ma le probabilità saranno conteggiate nel secondo caso e non nel primo.

Una caratteristica interessante nella costruzione di tali frattali è la presenza obbligatoria della formula di Bernoulli in tali funzioni. Le combinazioni sono evidenziate in rosa e i prodotti delle probabilità sono indicati in giallo. L'insieme di questi due moltiplicatori forma la formula di Bernoulli.

Verifichiamo ora due cose contemporaneamente: la correttezza della costruzione dell'intero frattale e l'ipotesi che il payoff atteso dipenda solo dalla capacità di previsione. Le fasi possono essere presentate come punti e come operazioni. In quest'ultimo caso i punti devono essere moltiplicati per il coefficiente di proporzionalità appropriato, che dipende dai lotti e dalla dimensione dei tick. In questo caso utilizzeremo i punti - questa rappresentazione è universale:

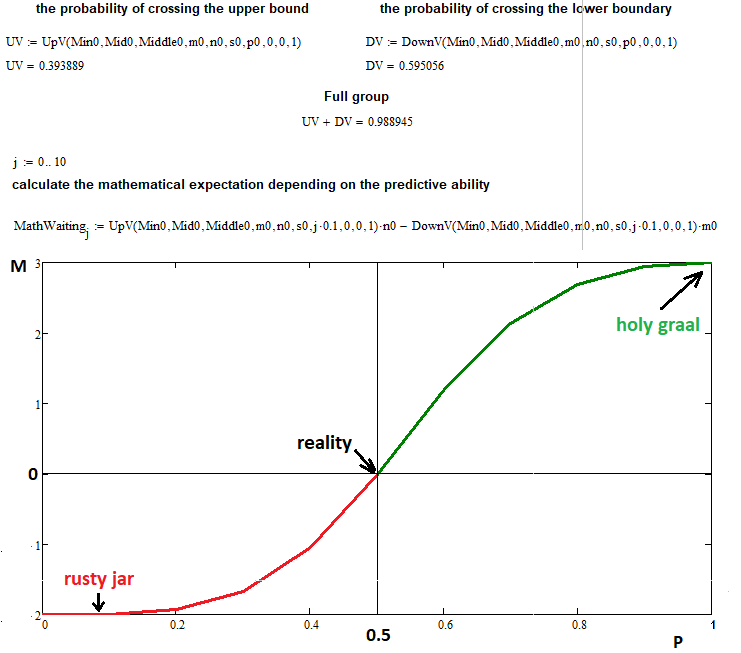
In questo esempio, ho utilizzato i seguenti dati di input per tracciare l'aspettativa matematica rispetto alla probabilità di un passo verso l’alto:

• n = 3 — numero di segmenti superiori
• m = 2 — numero di segmenti inferiori
• s = 22 — numero di passi consentiti per una reazione a catena della funzione frattale (se si aumenta questo valore, si creerà un carico supplementare sul computer, quindi questo numero di passi è sufficiente)
• 0 ... 0.1 ... 0.2 ...... 1,0 — dividendo l'intervallo delle probabilità di salita in 10 parti con un passo di 0,1

Come si può notare, per la probabilità di 0,5 l'aspettativa matematica per le nostre operazioni è pari a zero, come precedentemente previsto dalla formula. Ai punti estremi 0 e 1, il valore della funzione tende a "n" e "-m", il che conferma le nostre ipotesi. Il frattale ha portato a termine con successo il suo compito, anche se ha rivelato un inconveniente: un grande aumento del tempo e della complessità di calcolo. Tuttavia, è abbastanza accettabile aspettare un paio d'ore o addirittura un giorno per compiti simili.

Questo frattale funziona solo per i casi in cui n >= m, cioè quando la distanza dal bordo superiore è maggiore di quella dal bordo inferiore, ma non è necessario fornire questo dato nel frattale. Questa costruzione può essere speculare: se n < m, possiamo calcolare il frattale passando m al posto di n e n al posto di m. Quindi scambiare le probabilità e ottenere il risultato desiderato. Tali frattali possono essere utilizzati non solo per dimostrare formule, ma anche per un processo inverso. Alcune formule possono essere ottenute solo grazie all'uso dei frattali.

Riepilogo

Credo che in questo articolo siano state tratte le seguenti conclusioni molto importanti:

• La teoria della probabilità combinata con la programmazione può fornire una base teorica per descrivere molti processi di mercato.
• I frattali, combinati con le principali disposizioni della teoria della probabilità, possono rispondere alle domande più difficili.
• Abbiamo visto un esempio di creazione di un frattale piuttosto complesso.
• L'intera teoria è stata testata nella pratica utilizzando la programmazione nell'ambiente MathCad 15.
• L'articolo ha dimostrato che lo schema di Bernoulli offre l'opportunità di creare qualsiasi frattale con stati a due fasi.

Conclusioni

Spero che il lettore possa vedere in questo materiale qualcosa di nuovo, che possa essere utilizzato nella pratica del trading. Durante la stesura di questo articolo, ho cercato di trasmettere tutta la potenza della matematica discreta e della teoria della probabilità, in modo da prepararvi a un altro compito difficile — descrivere i processi di mercato utilizzando catene di probabilità frattali. Ho provato a combinare tutte le principali disposizioni della teoria della probabilità in un unico materiale, che può aiutare ulteriormente a risolvere compiti complessi per il trading pratico. Inoltre, ho cercato di eliminare tutti i dettagli irrilevanti. Il prossimo articolo fornirà nuovi esempi di applicazione pratica dei frattali e risposte ad altre importanti domande.