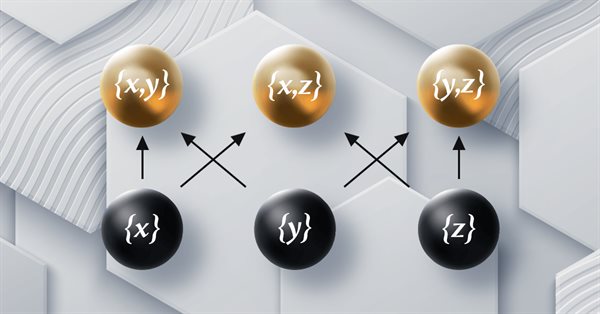
Kategorientheorie in MQL5 (Teil 12): Ordnungsrelationen

Einführung

Im vorangegangenen Artikel haben wir Graphen, die Eckpunkte und Pfeile eines zusammenhängenden Systems, im Rahmen der Kategorientheorie betrachtet und untersucht, wie verschiedene Pfade mit ihren Attributen zur Definition verschiedener Trailing-Stop-Methoden für ein typisches Handelssystem verwendet werden können.

In diesem Artikel befassen wir uns mit Ordnungsrelation im Rahmen der Kategorientheorie und der Frage, wie sie, wie in unserem vorherigen Artikel, Handels-Setups durch Trailing-Stops ergänzen können. Bei Ordnungen geht es ganz einfach darum, die „Größe“ verschiedener Elemente, die typischerweise in einer Menge vorkommen, zu ordnen. Sie verdeutlichen die Idee, dass die Elemente einer bestimmten Menge nach mehreren Kriterien geordnet werden können. Die Kategorientheorie fügt dem eine weitere Dimension hinzu, indem sie den Begriff der Menge der Mengen und sogar der Menge der Menge der Mengen (usw.) einführt. In diesem Artikel befassen wir uns daher mit den festgelegten Rangordnungen.

Insbesondere werden wir uns auf Muster in geordneten Mengen konzentrieren, um Handelsausstiege zu generieren. Es gibt eine Vielzahl von Mustern, die dabei in Betracht gezogen werden könnten, da unsere Liste von Preisaktionsmustern über Indikatormuster bis hin zu allgemeinen Multi-Asset-Indexmustern reichen könnte. In Anlehnung an die Schritte eines grundlegenden Handelssystems, die wir in früheren Artikeln betrachtet haben, werden wir jedoch die drei Intra-Schritte zwischen dem ersten und dem letzten Schritt unseres fünfstufigen Prozesses in Teilmengen umwandeln, um unsere geordneten Mengenmuster abzuleiten.

Das Verständnis von Ordnungen in der Kategorientheorie

Nach der Ordnungstheorie gibt es hauptsächlich drei Arten von Ordnungsrelationen: Quasiordnungen, Halbordnung und Totalordnungen. Lineare Ordnungsrelationen werden auch als Totalordnungen bezeichnet. Quasiordnungenen sind Rangordnungen von Mengenelementen, bei denen jedes Element der Menge mit allen anderen Elementen verglichen wird (Reflexivität) und die Ergebnisse jedes Vergleichs logische Auswirkungen auf andere Elementvergleiche haben (Transitivität). Quasiordnungenen tragen der Mehrdeutigkeit Rechnung: Wenn zwei Elemente gemäß der Binäroperation den gleichen Wert haben, können beide in die Ausgabemenge aufgenommen werden. Auch Quasiordnungenen können undefinierte Ergebnisse enthalten, die auftreten, wenn zwei Elemente nicht verglichen werden können, z. B. aufgrund von grundlegender Unähnlichkeit. Halbordnungen sind eine Art von Quasiordnungenen, die ein zusätzliches Konzept der Antisymmetrie einführen. Das bedeutet, dass nur eines der beiden Elemente in die Ausgabemenge aufgenommen wird, wenn bei der vergleichenden Binäroperation festgestellt wird, dass sie denselben Wert haben. Daher die Bezeichnung „Halb-“, da nur eines von mehreren gleichen Elementen ausgegeben wird. Schließlich sind lineare Ordnungsrelationen, die diesem Trend entsprechen, eine spezielle Form von Halbordnungen, bei denen es keine unbestimmten Ergebnisse gibt. Das bedeutet, dass alle Elemente vergleichbar sind. Wie bereits über die Quasiordnungenen gesagt, können einige Elemente unvergleichbar sein, was bedeutet, dass die binäre Operation ein undefiniertes Ergebnis liefert. Dies ist bei linearen Ordnungen nicht der Fall.

Formal ist also eine Menge S mit einer binären Beziehung R gegeben,

R ⊆ S x S

R würde allenfalls als Quasiordnung gelten:

s, s', s" ∈ S

haben wir Reflexivität, die formal wie folgt dargestellt wird:

s ≦ s

als auch die Transitivität, die durch impliziert wird:

s ≦ s' und s' ≦ s" bedeutet s ≦ s"

Halbordnungen, wie oben erwähnt, würden die Halbordnungen antisymmetrisch machen, sodass wenn:

s ≦ s' und s' ≦ s dann s = s'

was bedeutet, dass nur eines von s bzw. s' in der Ausgabe dargestellt wird.

Lineare Ordnungen würden Halbordnungen vergleichbar machen, sodass es für zwei beliebige Elemente eine eindeutige Beziehung zwischen beiden gibt:

s ≦ s' oder s' ≦ s

was bedeutet, dass undefinierte Ausgaben nicht berücksichtigt werden.

Wie bereits erwähnt, sind diese Ordnungsformate nützlich, um Muster zu markieren, die bei der Entscheidungsfindung in jedem Handelssystem helfen können. In diesem Artikel werden wir die in früheren Artikeln verwendeten schrittinternen, monoiden Mengen von Rückblickzeitraum, angewandtem Preis und Indikator wiederherstellen, während wir der Einfachheit halber die Endmengen von Zeitrahmen und Handelsaktion beibehalten. Der primär getestete Parameter ist die Entscheidungsreihenfolge, wie dies auch im vorherigen Artikel der Fall war. Da wir jedoch Halbordnungen berücksichtigen werden, besteht die Möglichkeit undefinierter Ergebnisse. Das bedeutet, dass die Reihenfolge der monoiden Mengen, die die Entscheidungspunkte darstellen, kleiner sein kann als die 3 Eingaben. Manchmal sind es auch 2 oder sogar 1. Dies bedeutet, dass wir in bestimmten Situationen möglicherweise nur 3 oder 4 Entscheidungen treffen müssen, anstatt der standardmäßigen 5, wenn wir beurteilen, ob wir unseren Stop-Loss ändern müssen.

Anwendung der Ordnungstheorie in MQL5

In diesem Artikel werden wir nicht auf die Quasiordnungenen eingehen, da ein solcher Artikel zu lang wäre. Vielmehr werden wir uns auf Halbordnungen und lineare Ordnungen konzentrieren. Da wir bereits über die Datenstrukturen verfügen, die unsere fünf Handelsschritte gemäß dem vorangegangenen Artikel definieren, ist das Wichtigste, was für die Implementierung der Ordnungstheorie noch aussteht, die binären Funktionen, die unsere Datenstrukturen verarbeiten und eine Menge ausgeben (typischerweise eine Teilmenge der Eingaben). Da wir uns auf Halbordnungen und lineare Ordnungen konzentrieren, gibt es für jeden eine Funktion.

Es mag sinnvoll sein, die Unterschiede und die relativen Vorteile der beiden Formen der Ordnungen, die wir in diesem Artikel betrachten, hervorzuheben. Wie bereits erwähnt, erlauben Halbordnungen im Gegensatz zu linearen Ordnungen undefinierte Klassifikationen. Dies kann in einer Reihe von Szenarien nützlich sein. Betrachten wir ein einfaches Beispiel für die Einstufung von Kursbalken in einem Chart als auf- oder abwärts. In diesem Prozess werden Sie zwangsläufig auf eine langbeinige Doji-Kerze stoßen, die streng genommen weder auf- oder abwärts gerichtet ist. Bei einer linearen Klassifizierung müsste dieser Datenpunkt weggelassen werden, da er das Vergleichbarkeitsaxiom verletzen würde.

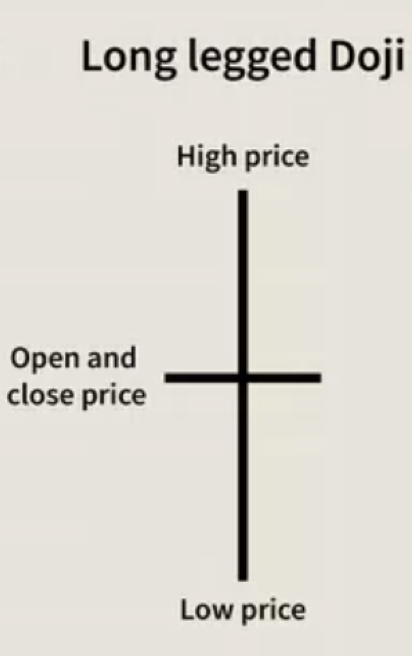
Bei der Halbordnung jedoch wäre der Ausgabesatz durch die Einbeziehung dieses Datenpunkts und damit seines Ergebnisses vollständiger und repräsentativer für den Datensatz. Um zu zeigen, warum dies von Bedeutung ist, neigen „langbeinige“ Doji-Kerzen und andere Kerzen wie der Gravestone Doji und der Dragonfly Doji dazu, in wichtigen Preisunterstützungs- und -widerstandsregionen zu erscheinen. Wenn Ihre Klassifizierung also eines dieser Muster auslässt, werden Ihre Analysen und damit auch Ihre Prognosen zwangsläufig weniger genau sein, denn für die meisten Handelssysteme spielen die langfristigen Preisunterstützungs- und -widerstandsregionen eine entscheidende Rolle bei der Festlegung von Handels-Setups. Die Hinzufügung der Antisymmetrieeigenschaft bei der Erstellung von Halbordnungen kann somit zur besseren Filterung von Handelssignalen genutzt werden.

Eine Fallstudie über ein Handelssystem, das sich von unserem 5-Schritte-Prozess unterscheidet, den wir in früheren Artikeln betrachtet haben, könnte Preisbalkenmuster vektorisiert haben. Indem wir jede Preisbalkenformation als Vektor haben, der einfach ein Array von Gewichten ist, können wir vergleichen, wie ähnlich verschiedene Muster sind. Wenn wir über einen angemessenen Zeitraum trainieren und eventuelle Kursformationen für eine beträchtliche Anzahl von vektorisierten Mustern identifizieren, können wir jedes neue Muster mit dem vergleichen, was trainiert wurde, und auf der Grundlage des euklidischen Abstands zu diesen trainierten Mustern kann das Muster, das unserem neuen Muster am nächsten kommt, mit seiner Postkursformation als wahrscheinlichstes Ergebnis unseres neuen Musters dienen.

Lineare Ordnungen können in Fällen der Portfolioanalyse Halbordnungen vorgezogen werden. Bei einer Vielzahl von Vermögenswerten, die bewertet oder in ein Portfolio aufgenommen werden müssen, wäre eine lineare Anordnung mit strenger einheitlicher Gewichtungsanforderung (Vergleichbarkeit) ein Kinderspiel. Dafür gibt es eine Reihe von Gründen, von denen einige als selbstverständlich angesehen werden. Lineare Ordnungen ermöglichen eine sequentielle Bewertung der Anlagen, was einen rationellen Prozess ermöglicht. Unabhängig von der Anzahl der Vermögenswerte werden die Prioritäten bereits durch die Gewichtung der Vermögenswerte festgelegt, die ein Wert sein kann, der alles vom in der Vergangenheit realisierten Wert bis zum künftigen potenziellen Risiko quantifiziert. Dies führt nicht nur zu mehr Effizienz, sondern bietet dem Händler auch die Möglichkeit, nicht alle möglichen Vermögenswerte zu berücksichtigen, indem er sich auf diese konzentriert.

Diese Priorisierung bedeutet, dass die wichtigsten Vermögenswerte bei ihren Investitionsentscheidungen zuerst berücksichtigt werden, was zu der kritischen Frage der Vermögensverteilung führt. Wie werden die einzelnen Vermögenswerte innerhalb des Portfolios eingeteilt? Bei einer linearen Anordnung kann die Gewichtung jedes Vermögenswerts oft als fairer Näherungswert dafür dienen, wie viel Kapital für den Erwerb des Vermögenswerts eingesetzt werden sollte, was bei einer Halbordnung schwieriger zu bewerkstelligen wäre.

Fallstudie: Entwicklung eines Handelssystems mit Ordnungsrelation

Die gewählte Handelsstrategie, die auf dem System aufbaut, das wir in den vorangegangenen Artikeln betrachtet haben, beinhaltet die Auswahl der Zwischenschritte 2 bis 4 unserer 5-Schritte-Methode. Wir werden diese nach der Methode der Halbordnung in einem Handelssystem und nach der linearen Ordnung in einem anderen System auswählen.

Für die Auswahl der Teilreihenfolge sind alle unsere Monoidmengen auf Anhieb unvergleichbar, da wir eine Rückblickperiode haben, die ein Ganzzahlentyp ist, wir haben einen angewandten Preis, der eine Enumeration ist, und schließlich einen Indikatortyp, der streng genommen auch eine String-Auswahl ist. Um also eine gewisse Fähigkeit zur Verwendung des binären Operators einzuführen:

≦

Wir werden nur ein Paar der Sätze normalisieren und den dritten in seinem Standardformat belassen. Die Eingaben der Funktion, die den Halbordnungen ausführt, sind naturgemäß Preisaktionen. Die Preisparameter, die wir als Inputs für unsere Funktionen von Halbordnungen betrachten, sind Autokorrelationsindizes. Wir werden einfach Indizes verschiedenen Autokorrelationsmustern zuordnen, und für jeden Index werden wir ein bestimmtes Paar von Sets normalisiert haben, das dann unsere ausgewählte Set-Reihenfolge für unser Handelssystem bestimmen wird. Bei Halbordnungen bedeutet das Vorhandensein unbestimmter Mengen, dass nur zwei Mengen ausgewählt werden, was bedeutet, dass wir mit ziemlicher Sicherheit immer mit einem 4-Schritt-Prozess enden werden und nicht mit dem 5-Schritt-Prozess, den wir bisher verwendet haben.

Bei linearen Ordnungen werden jedoch alle monoiden Mengen normalisiert. Dies sollte uns die vollen 5 Schritte geben, die wir in Betracht gezogen haben, und wie bei den Halbordnungen wird die Eingabe für die lineare Ordnungsfunktion unser Autokorrelationsindex sein. Die Zuordnung des Autokorrelationsindexes wird rudimentär sein, wie aus der folgenden Auflistung ersichtlich ist.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CTrailingCT::Ordering(int Lookback)
   {
      m_low.Refresh(-1);
      m_high.Refresh(-1);
      m_close.Refresh(-1);
      
      double _c[],_l[],_h[];
      
      ArrayResize(_c,Lookback);ArrayInitialize(_c,0.0);
      ArrayResize(_l,Lookback);ArrayInitialize(_l,0.0);
      ArrayResize(_h,Lookback);ArrayInitialize(_h,0.0);
      
      for(int i=0;i<Lookback;i++)
      {
         _c[i]=m_close.GetData(i);
         _l[i]=m_low.GetData(Lookback+i);
         _h[i]=m_high.GetData(Lookback+i);
      }
      
      double _r_h=0.0,_r_l=0.0;
      
      if(MathCorrelationSpearman(_c,_l,_r_l) && MathCorrelationSpearman(_c,_h,_r_h))
      {
         if(_r_l>=__PHI){ LongIndex(5); }
         else if(_r_l>=1.0-__PHI){ LongIndex(4); }
         else if(_r_l>=0.0){ LongIndex(3); }
         else if(_r_l>=(-1.0+__PHI)){ LongIndex(2); }
         else if(_r_l>=(-__PHI)){ LongIndex(1); }
         else{ LongIndex(0);}
         
         if(_r_h>=__PHI){ ShortIndex(5); }
         else if(_r_h>=1.0-__PHI){ ShortIndex(4); }
         else if(_r_h>=0.0){ ShortIndex(3); }
         else if(_r_h>=(-1.0+__PHI)){ ShortIndex(2); }
         else if(_r_h>=(-__PHI)){ ShortIndex(1); }
         else{ ShortIndex(0);}
         
         return(true);
      }
      
      return(false);
   }

Zu Beginn wird unser Code für die Verarbeitung von Halbordnungen in die Kauf- und Verkaufs-Trailing-Stop-Verarbeitungsfunktionen eingebettet, wie im Anhang am Ende des Artikels beschrieben. Bemerkenswert ist hier, dass jeder zugewiesene Index im Wesentlichen nur zwei Mengen abbildet, da die dritte Menge nicht definiert ist. Die durch die einzelnen möglichen Indizes definierte Reihenfolge bedeutet, dass der erste zugewiesene Satz eine höhere Gewichtung hat als der letzte zugewiesene Satz. Die Notwendigkeit, eine Normalisierungsfunktion zu entwickeln, die den einzelnen Werten ein physisches Gewicht verleiht, wird daher verneint, da sie das Endergebnis nicht wesentlich beeinflussen wird.

Ebenso wird die lineare Ordnungsfunktion wie folgt aufgeführt:

	ENUM_TIMEFRAMES _timeframe=GetTimeframe(m_timeframe,__TIMEFRAMES);
         
         int _lookback=m_default_lookback;
         ENUM_APPLIED_PRICE _appliedprice=__APPLIEDPRICES[m_default_appliedprice];
         double _indicator=m_default_indicator;
         
         if(m_long_index==0)
         {
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe);
            _indicator=GetIndicator(_lookback,_timeframe,_appliedprice);
         }
         else if(m_long_index==1)
         {
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _indicator=GetIndicator(_lookback,_timeframe,_appliedprice);
         }
         else if(m_long_index==2)
         {
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,__LOOKBACKS[m_default_lookback],_timeframe);
            _indicator=GetIndicator(m_default_lookback,_timeframe,_appliedprice);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
         }
         else if(m_long_index==3)
         {
            _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,m_default_lookback,_timeframe);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
         }
         else if(m_long_index==4)
         {
            _indicator=GetIndicator(__LOOKBACKS[m_default_lookback],_timeframe,__APPLIEDPRICES[m_default_appliedprice]);
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe);
         }
         else if(m_long_index==5)
         {
            _lookback=GetLookback(m_lookback,__LOOKBACKS,_timeframe);
            _indicator=GetIndicator(_lookback,_timeframe,__APPLIEDPRICES[m_default_appliedprice]);
            _appliedprice=GetAppliedprice(m_appliedprice,__APPLIEDPRICES,_lookback,_timeframe);
         }
         //
         int _trade_decision=GetTradeDecision(_timeframe,_lookback,_appliedprice,_indicator);

Bemerkenswert ist dabei, dass jeder Index alle Mengen vollstä#ndig auflistet, da die Vergleichbarkeit eine Voraussetzung für alle Mengen ist. Und wie bereits erwähnt, wird auf die Zuweisung von Gewichtungszahlen für jeden Satz, die dann bei der Sortierung verwendet werden, verzichtet, da die verwendete Indizierung eine Gewichtungsreihenfolge impliziert, die wie oben gezeigt umgesetzt wird.

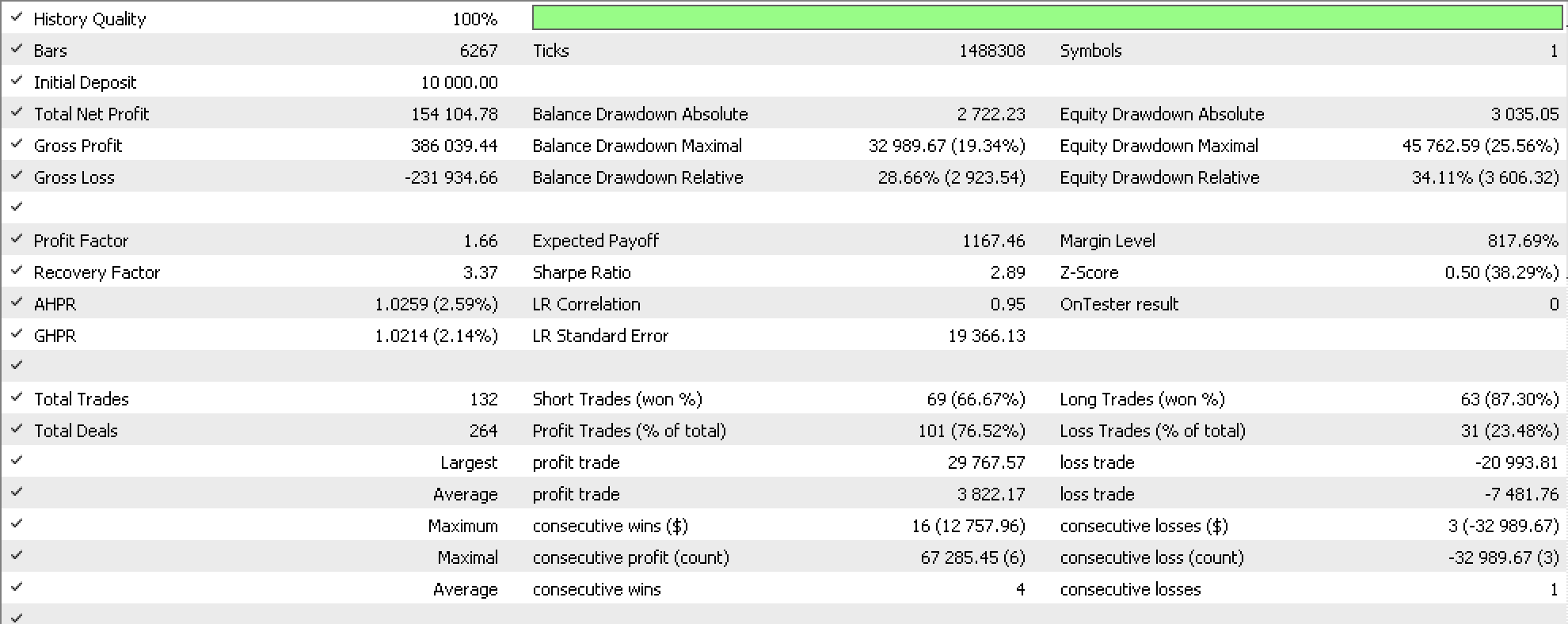
Wenn wir Tests mit unseren neuen Trailing-Klassen auf einer Signalklasse der Bibliothek Awesome Oscillator mit fester Marge für das Symbol USDJPY für die letzten 12 Monate durchführen, erhalten wir die folgenden Berichte für jede der Ordnungsmethoden. Der erste ist der Bericht über die Methode von Halbordnungen.

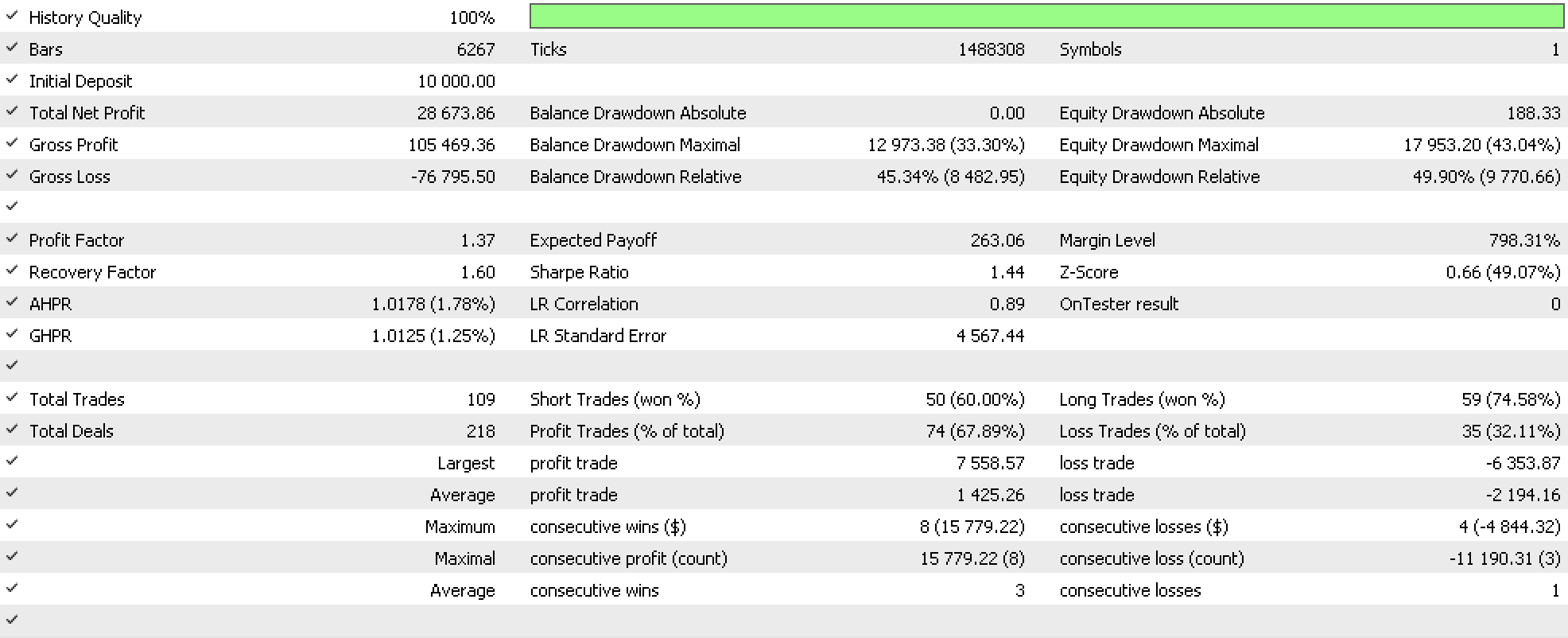
Unser Expertenberater erzielt mehr als 100.000 Euro Gewinn mit Einstellungen, die, wie immer in diesen Artikelserien, keine Kursziele für Take-Profit oder Stop-Loss verwenden, sondern Positionen nur so lange halten, bis der Signalindikator entscheidet, dass sie geschlossen werden sollten. Da wir unseren Trailing-Stop verfeinern, waren die meisten profitablen geschlossenen Positionen tatsächlich auf unseren Trailing-Stop zurückzuführen, was für die Vorzüge von Halbordnungen bei der Generierung zuverlässiger Trailing-Stop-Angaben spricht. Wir haben auch lineare Ordnungsrelation auf Basis von Trailing-Stops getestet, was den folgenden Bericht ergab.

Überraschenderweise ist dieses Ergebnis nicht so gewinnbringend wie das, das wir mit Halbordnungen („mehrdeutigen“ akkommodierenden) hatten. Seltsamerweise ist der Aktienverlust bei weniger Geschäften noch größer. Um endgültige Schlussfolgerungen ziehen zu können, sind Tests über längere Zeiträume und mit mehreren Symbolen erforderlich, aber es könnte sicher sein, dass Halbordnungen vielversprechender sind als lineare Ordnungen.

Schlussfolgerung

In diesem Artikel wurde die Wirksamkeit von Halbordnungen im Vergleich zu linearen Ordnungen beim Setzen und Ändern von Trailing-Stops für einen typischen Expert Advisor untersucht. Zuvor haben wir die relativen Vorteile dieser beiden Ordnungsprinzipien erwogen und das Ankerordnungsprinzip der beiden, nämlich die Quasiordnungen, nicht betrachtet, da dies den Artikel zu lang gemacht hätte, ohne einen sinnvollen Beitrag zum Inhalt zu leisten. Denken Sie daran, dass Halbordnungen eine spezielle Form von Quasiordnungen sind, während lineare Ordnungen ebenfalls eine spezielle Form von Halbordnungen sind. Da es bei der grundlegenden Definition dieser Ordnungstypen viele Überschneidungen gibt, haben wir uns auf die letzten beiden konzentriert.

Die Methoden der Theorien von Halbordnungen und linearen Ordnungen wurden aufgrund ihrer spezifischen Vorteile genutzt. Halbordnungen ermöglichen mehr Flexibilität bei der Klassifizierung von Rohdatensätzen, was zu einer umfassenderen und genaueren Analyse führen kann. Umgekehrt erfordert eine lineare Ordnung, die strenger ist, eine Normalisierung der Rohdaten, um die Vergleichbarkeit zu gewährleisten, was zu einer allgemeinen Priorisierung und Effizienz bei der Entscheidungsfindung führt.

Diese Ordnungsmethoden haben das Potenzial, in diesen Ordnungsreihen weiter erforscht und verfeinert zu werden, wenn wir damit beginnen, die bereits behandelten Konzepte in einige neue zu integrieren, die wir uns ansehen werden.