MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 12): Das Newton-Polynom

Einführung

Die Zeitreihenanalyse spielt nicht nur eine wichtige Rolle bei der Unterstützung der Fundamentalanalyse, sondern kann auf sehr liquiden Märkten wie dem Devisenmarkt der Hauptfaktor für Entscheidungen darüber sein, wie man sich an den Märkten positioniert. Herkömmliche technische Indikatoren neigen dazu, dem Markt stark hinterherzuhinken, was sie bei den meisten Händlern in Ungnade fallen ließ, was zum Aufkommen von Alternativen führte, von denen die neuronalen Netze derzeit vielleicht die wichtigste sind. Aber was ist mit polynomieller Interpolation?

Sie bieten einige Vorteile, vor allem weil sie leicht zu verstehen und umzusetzen sind, da sie die Beziehung zwischen vergangenen Beobachtungen und zukünftigen Prognosen in einer einfachen Gleichung explizit darstellen. Dies hilft zu verstehen, wie sich vergangene Daten auf zukünftige Werte auswirken, was wiederum zur Entwicklung umfassender Konzepte und möglicher Theorien über das Verhalten der untersuchten Zeitreihen führt.

Da sie sowohl an lineare als auch an quadratische Beziehungen angepasst werden können, sind sie außerdem flexibel für verschiedene Zeitreihen und vielleicht noch relevanter für Händler, da sie in der Lage sind, mit verschiedenen Markttypen zurechtzukommen (z. B. zwischen schwankenden und trendigen oder volatilen und ruhigen Märkten).

Außerdem sind sie in der Regel nicht rechenintensiv und im Vergleich zu alternativen Ansätzen wie neuronalen Netzen relativ leicht. Das oder die in diesem Artikel untersuchten Modelle haben keinerlei Speicherbedarf, wie er beispielsweise bei einem neuronalen Netz besteht, bei dem je nach seiner Architektur die Speicherung einer Menge optimaler Gewichte und Verzerrungen nach jedem Training erforderlich ist.

Formal ist das Newtonsche Interpolationspolynom N(x) durch folgende Gleichung definiert:

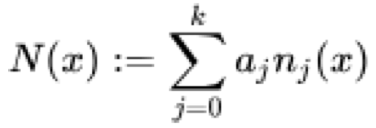
wobei alle x j in der Reihe eindeutig sind und a j die Summe der geteilten Differenzen ist, während n j (x) die Produktsumme der Basiskoeffizienten für x ist, die formal wie folgt dargestellt wird:

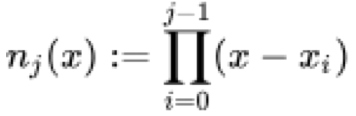
Die Formeln für die geteilten Differenzen und die Basiskoeffizienten können leicht unabhängig voneinander nachgeschlagen werden, aber wir wollen versuchen, ihre Definitionen hier so informell wie möglich zu formulieren.

Geteilte Differenzen sind ein sich wiederholender Divisionsprozess, bei dem die Koeffizienten für x bei jedem Exponenten festgelegt werden, bis alle x Exponenten aus dem bereitgestellten Datensatz ausgeschöpft sind. Betrachten wir zur Veranschaulichung das folgende Beispiel mit drei Datenpunkten:

(1,2), (3,4), und (5,6)

Damit die geteilte Differenz verwendet werden kann, müssen alle x-Werte eindeutig sein. Aus der Anzahl der bereitgestellten Datenpunkte lässt sich der höchste Exponent von x im abgeleiteten Polynom der Newton-Form ableiten. Hätten wir zum Beispiel nur 2 Punkte, dann wäre unsere Gleichung einfach linear in der Form:

y = mx + c.

Das bedeutet, dass unser höchster Exponent eins ist. Für unser Drei-Punkte-Beispiel ist der höchste Exponent also 2, was bedeutet, dass wir 3 verschiedene Koeffizienten für unser abgeleitetes Polynom benötigen.

Die Ermittlung jedes dieser 3 Koeffizienten ist ein schrittweiser, iterativer Prozess, bis wir zum dritten Koeffizienten gelangen. In den oben genannten Links finden Sie Formeln, aber am besten lässt sich dies anhand einer Tabelle wie der folgenden veranschaulichen:

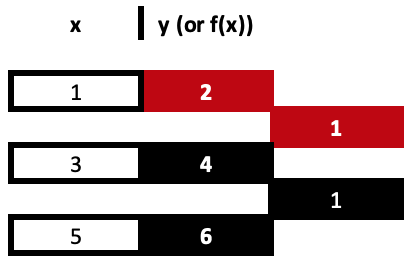
Unsere erste Spalte mit den geteilten Differenzen ergibt sich also aus der Division der Differenz zwischen den y-Werten und der Veränderung der jeweiligen x-Werte. Denken Sie daran, dass alle x-Werte eindeutig sein müssen. Diese Berechnungen sind sehr einfach und geradlinig, aber sie lassen sich leichter anhand einer Tabelle wie oben gezeigt nachvollziehen als anhand der typischen Formeln, auf die in den gemeinsamen Links verwiesen wird. Beide Ansätze führen zu demselben Ergebnis.

= (4 - 2) / (3 - 1)

Das gibt uns unseren ersten Koeffizienten, 1.

= (6 - 4) / (5 - 3)

Das gibt uns den zweiten Koeffizienten mit gleichem Wert. Die Koeffizienten sind rot hervorgehoben.

In unserem Beispiel mit 3 Datenpunkten würde der Endwert seine y-Differenzen aus den soeben berechneten Werten erhalten, aber seine x-Nenner

wären die beiden Extremwerte in der x-Reihe, da ihre Differenz der Divisor sein wird, sodass unsere Tabelle wie folgt aussehen würde:

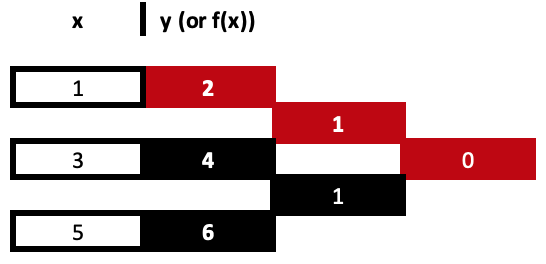
Mit unserer ausgefüllten Tabelle oben haben wir 3 abgeleitete Werte, aber nur 2 davon werden für die Berechnung der Koeffizienten verwendet. Dies führt uns also zu den Produktsummen der „Basispolynome“. So ausgefallen es auch klingt, es ist wirklich einfach, sogar noch einfacher als die geteilten Unterschiede. Zur Veranschaulichung: Auf der Grundlage der aus der obigen Tabelle abgeleiteten Koeffizienten würde unsere Gleichung für die drei Punkte lauten:

y = 2 + 1*(x - 1) + 0*(x - 1)*(x - 3)

dies führt zu:

y = x + 1

Die hinzugefügten Klammern sind alles, was die Basispolynome ausmacht. Der x n-Wert ist einfach der jeweilige x-Wert für jeden abgetasteten Datenpunkt. Nun zurück zu den Koeffizienten, und Sie werden feststellen, dass wir in der Regel nur die oberen Werte der Tabelle verwenden, um diese Klammerwerte voranzustellen, und wenn wir nach rechts fortschreiten, indem wir kürzere Spalten in der Tabelle erhalten, stellen die oberen Werte längere Klammersequenzen vor, bis alle vorgesehenen Datenpunkte berücksichtigt sind. Wie bereits erwähnt, je mehr Datenpunkte interpoliert werden, desto mehr Exponenten von x und damit desto mehr Spalten haben wir in unserer Ableitungstabelle.

Bevor wir uns der Umsetzung zuwenden, wollen wir dies noch einmal anschaulich illustrieren. Angenommen, wir haben 7 Datenpunkte für Wertpapierkurse, wobei die x-Werte einfach der Preisbalkenindex sind, wie unten gezeigt:

0	1.25590
1	1.26370
2	1.25890
3	1.25395
4	1.25785
5	1.26565
6	1.26175

Unsere Tabelle, die die Koeffizientenwerte weitergibt, würde sich wie folgt um 8 Spalten erweitern:

Tabelle mit 8 Spalten mit geteilten Differenzen:

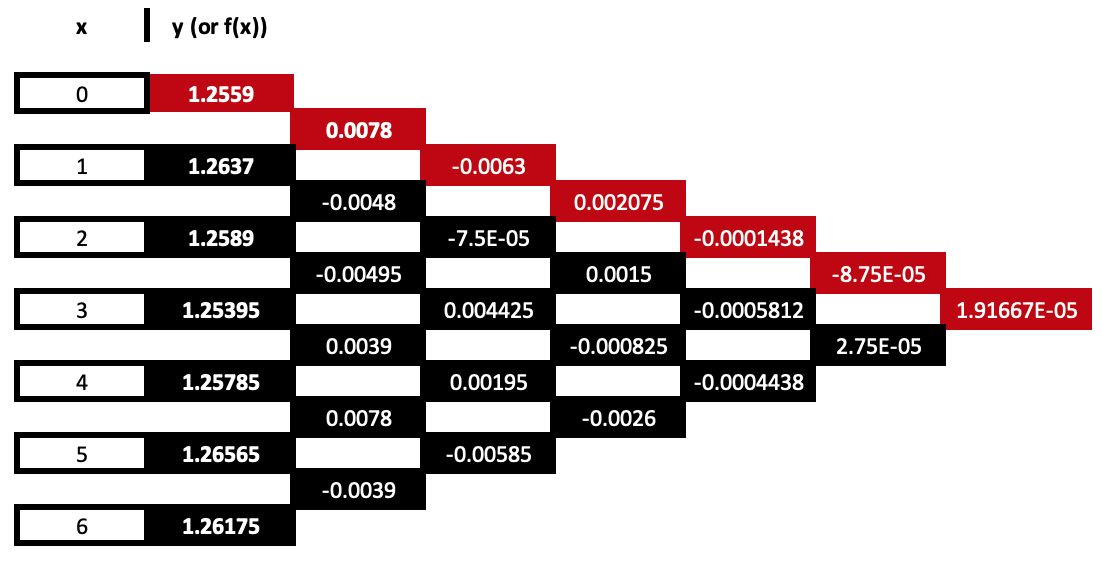
Mit den rot hervorgehobenen Koeffizienten würde die Gleichung demnach wie folgt lauten:

y = 1,2559 + 0,0078*(x - 0) - 0,0063*(x - 0)*(x - 1) + ...

Diese Gleichung geht, wie man sieht, bis zum Exponenten 6, wenn man die sieben Datenpunkte betrachtet, und ihre Hauptfunktion könnte wohl in der Vorhersage des nächsten Wertes bestehen, indem man einen neuen x-Index in die Gleichung eingibt. Wenn die Beispieldaten „als Zeitreihe“ eingestellt wurden, wäre der nächste Index -1, andernfalls wäre er 8.

MQL5-Implementierung:

Die Umsetzung in MQL5 ist mit minimalem Programmieraufwand möglich, obwohl ich keine Bibliotheken gefunden habe, die es ermöglichen, diese Ideen beispielsweise aus vorcodierten Klasseninstanzen auszuführen.

Um dies zu erreichen, müssen wir im Wesentlichen zwei Dinge tun. Zunächst benötigen wir eine Funktion, mit der wir die Koeffizienten für x für unsere Gleichung aus unserem Stichproben-Datensatz berechnen können. Zweitens brauchen wir auch eine Funktion, die einen Prognosewert mit Hilfe unserer Gleichung verarbeitet, wenn ein x-Wert vorliegt. Das hört sich alles ziemlich einfach an, aber wenn man bedenkt, dass wir dies in einer skalierbaren Art und Weise tun wollen, muss man bei den Verarbeitungsschritten ein paar Vorbehalte beachten.

Bevor wir uns damit befassen, sollten wir uns vielleicht fragen, was mit „skalierbarer Weise“ gemeint ist. Damit meine ich einfach Funktionen, die geteilte Differenzen verwenden können, um Koeffizienten für Datensätze zu ermitteln, deren Größe nicht vorgegeben ist. Es mag offensichtlich klingen, aber wenn wir unser allererstes Beispiel mit 3 Datenpunkten betrachten, wird die MQL5-Implementierung dieses Verfahrens zur Ermittlung der Koeffizienten weiter unten beschrieben.

Die folgende Auflistung folgt einfach den Gleichungen, um die geteilte Differenz für die beiden Paare innerhalb der abgetasteten Daten zu erhalten, und iteriert dieses Verfahren, um auch den letzten Wert zu erhalten. Wenn wir nun eine Stichprobe mit 4 Datenpunkten hätten, würde die Interpolation ihrer Gleichung eine andere Funktion erfordern, da wir mehr Schritte machen müssen als im obigen 3-Punkte-Beispiel.

Wenn wir also eine skalierbare Funktion haben, wäre sie in der Lage, n große Datensätze zu verarbeiten und n-1 Koeffizienten auszugeben. Dies wird durch die folgende Auflistung realisiert:

//+------------------------------------------------------------------+
//| INPUT PARAMETERS                                                 |
//|     X   -   vector with x values of sampled data                 |
//|     Y   -   vector with y values of sampled data                 |
//| OUTPUT PARAMETERS                                                |
//|     W   -   vector with coefficients.                            |                                          |
//+------------------------------------------------------------------+
void Cnewton::Set(vector &W, vector &X, vector &Y)
{  vector _w[];
   ArrayResize(_w, int(X.Size() - 1));
   int _x_scale = 1;
   int _y_scale = int(X.Size() - 1);
   for(int i = 0; i < int(X.Size() - 1); i++)
   {  _w[i].Init(_y_scale);
      for(int ii = 0; ii < _y_scale; ii++)
      {  if(X[ii + _x_scale] != X[ii])
         {  if(i == 0)
            {  _w[i][ii] = (Y[ii + 1] - Y[ii]) / (X[ii + _x_scale] - X[ii]);
            }
            else if(i > 0)
            {  _w[i][ii] = (_w[i - 1][ii + 1] - _w[i - 1][ii]) / (X[ii + _x_scale] - X[ii]);
            }
         }
         else
         {  printf(__FUNCSIG__ + " ERR!, identical X value: " + DoubleToString(X[ii + _x_scale]) + ", at: " + IntegerToString(ii + _x_scale) + ", and: " + IntegerToString(ii));
            return;
         }
      }
      _x_scale++;
      _y_scale--;
      W[i + 1] = _w[i][0];
      if(_y_scale <= 0)
      {  break;
      }
   }
}

Diese Funktion arbeitet mit zwei verschachtelten for-Schleifen und zwei Ganzzahlen, die Indizes für x- und y-Werte enthalten. Es mag nicht der effizienteste Weg sein, dies zu implementieren, aber es funktioniert und in Ermangelung einer Standardbibliothek, die dies implementiert, würde ich dazu ermutigen, es zu erforschen und sogar Verbesserungen daran vorzunehmen, je nach Anwendungsfall.

Die Funktion für die Verarbeitung des nächsten y bei einer x-Eingabe und allen Koeffizienten unserer Gleichungen ist ebenfalls unten angegeben:

//+------------------------------------------------------------------+
//| INPUT PARAMETERS                                                 |
//|     W   -   vector with pre-computed coefficients                |
//|     X   -   vector with x values of sampled data                 |
//|     XX  -   query x value with unknown y                         |
//| OUTPUT PARAMETERS                                                |
//|     YY  -   solution for unknown y.                              |  
//+------------------------------------------------------------------+
void Cnewton::Get(vector &W, vector &X, double &XX, double &YY)
{  YY = W[0];
   for(int i = 1; i < int(W.Size()); i++)
   {  double _y = W[i];
      for(int ii = 0; ii < i; ii++)
      {  _y *= (XX - X[ii]);
      }
      YY += _y;
   }
}

Dies ist auch einfacher als unsere vorherige Funktion, obwohl sie auch eine verschachtelte Schleife hat. Wir verfolgen nur die Koeffizienten, die wir in der Set-Funktion erhalten haben, und ordnen sie dem entsprechenden Newton-Basis-Polynom zu.

Anwendungen:

Die Anwendungsmöglichkeiten sind vielfältig, und in diesem Artikel werden wir untersuchen, wie diese Methode als Signal, als Trailing-Stop-Methode und als Geldmanagement-Methode eingesetzt werden kann. Bevor diese kodiert werden, ist es normalerweise eine gute Idee, eine Ankerklasse mit den beiden Funktionen zu haben, die die Interpolation implementieren, deren Code oben aufgeführt ist. Für eine solche Klasse wird die Schnittstelle wie folgt aussehen:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnewton
{
private:

public:
                     Cnewton();
                    ~Cnewton();
   void              Set(vector &W, vector &X, vector &Y);
   void              Get(vector &W, vector &X, double &XX, double &YY);
};

Signal

Die Dateien der Klassen der standardmäßigen Signale für Experten, die in der MQL5-Bibliothek enthalten sind, dienen wie immer als guter Leitfaden für die Entwicklung einer eigenen Implementierung. In unserem Fall wären die erste offensichtliche Wahl für die Eingabe von Stichprobendaten zur Erstellung des Polynoms die Schlusskurse von Rohtiteln. Um ein Polynom auf der Grundlage von Schlusskursen zu erstellen, würden wir zunächst die x- und y-Vektoren mit den Indizes der Kursbalken bzw. den tatsächlichen Schlusskursen füllen. Diese beiden Vektoren sind die Schlüsseleingaben für unsere Funktion „set“, die für die Ermittlung der Koeffizienten zuständig ist. Es ist jedoch möglich, Alternativen zu verwenden, wie z.B. die Sitzungen eines Handelstages oder einer Handelswoche, vorausgesetzt natürlich, dass sich keine dieser Sitzungen in der Datenprobe wiederholt, d.h. dass sie alle nur einmal vorkommen, z.B. wenn Ihr Handelstag 4 Sitzungen hat, dann können Sie nicht mehr als 4 Datenpunkte zur Verfügung stellen und die Sitzungsindizes 0, 1, 2 und 3 können nur einmal im Datensatz vorkommen.

Nachdem wir unsere x- und y-Vektoren gefüllt haben, sollte der Aufruf der Funktion „set“ die vorläufigen Koeffizienten für unsere Polynomgleichung liefern. Wenn wir diese Gleichung mit diesen Koeffizienten und dem nächsten x-Wert mit der Funktion „get“ ausführen, erhalten wir die Projektion für den nächsten y-Wert. Da unsere y-Eingabewerte in der Set-Funktion Schlusskurse waren, würden wir den nächsten Schlusskurs suchen. Der Code dafür ist weiter unten zu finden:

   double _xx = -1.0;//m_length + 1.0,
   double _yy = 0.0;
   __N.Get(_w, _xx, _yy);

Zusätzlich zur Ermittlung des nächsten projizierten Schlusskurses geben die Check-Open-Funktionen der Klasse der Expertensignale in der Regel eine ganze Zahl im Bereich von 0 bis 100 aus, die angibt, wie stark das Kauf- oder Verkaufssignal ist. In unserem Fall müssen wir daher einen Weg finden, den voraussichtlichen Schlusskurs als einfache ganze Zahl darzustellen, die in diesen Bereich passt.

Um diese Normalisierung zu erhalten, wird die voraussichtliche Preisänderung bei Börsenschluss als Prozentsatz der aktuellen Preisspanne zwischen Hoch und Tief ausgedrückt. Dieser Prozentsatz wird dann als ganze Zahl im Bereich von 0 bis 100 ausgedrückt. Dies bedeutet, dass negative Schlusskursänderungen in der Funktion „Prüfung auf offene Kauf-Positionen“ automatisch gleich Null sind, ebenso wie positive Prognoseänderungen in der Funktion „Prüfung auf offene Verkaufs-Positionen“.

   m_high.Refresh(-1);
   m_low.Refresh(-1);
   m_close.Refresh(-1);
   int _i = StartIndex();
   double _h = m_high.GetData(m_high.MaxIndex(_i,m_length));
   double _l = m_low.GetData(m_low.MinIndex(_i,m_length));
   double _c = m_close.GetData(0);
//
   if(_yy > _c)
   {  _result = int(round(((_yy - _c) / (fmax(_h, fmax(_yy, _c)) - fmin(fmin(_yy, _c), _l))) * 100.0));
   }

Bei der Erstellung von Prognosen mit Hilfe der Polynomgleichung ist die einzige Variable, die wir verwenden, die Länge des Rückblickzeitraums (der den Umfang der Stichprobendaten festlegt). Diese Variable wird mit „m_length“ bezeichnet. Wenn wir Optimierungen nur für diesen Parameter für das Symbol EURJPY auf dem 1-Stunden-Zeitrahmen über das Jahr 2023 durchführen, erhalten wir die folgenden Berichte.

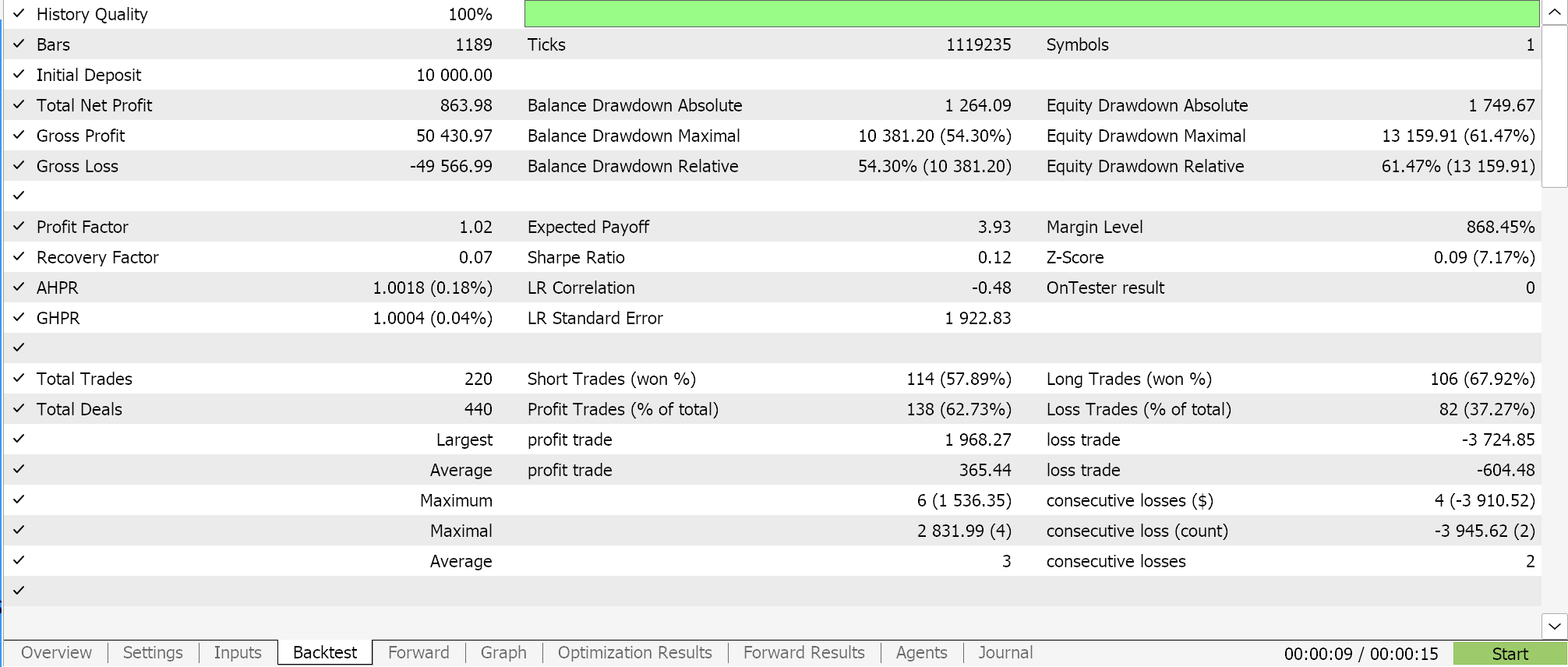
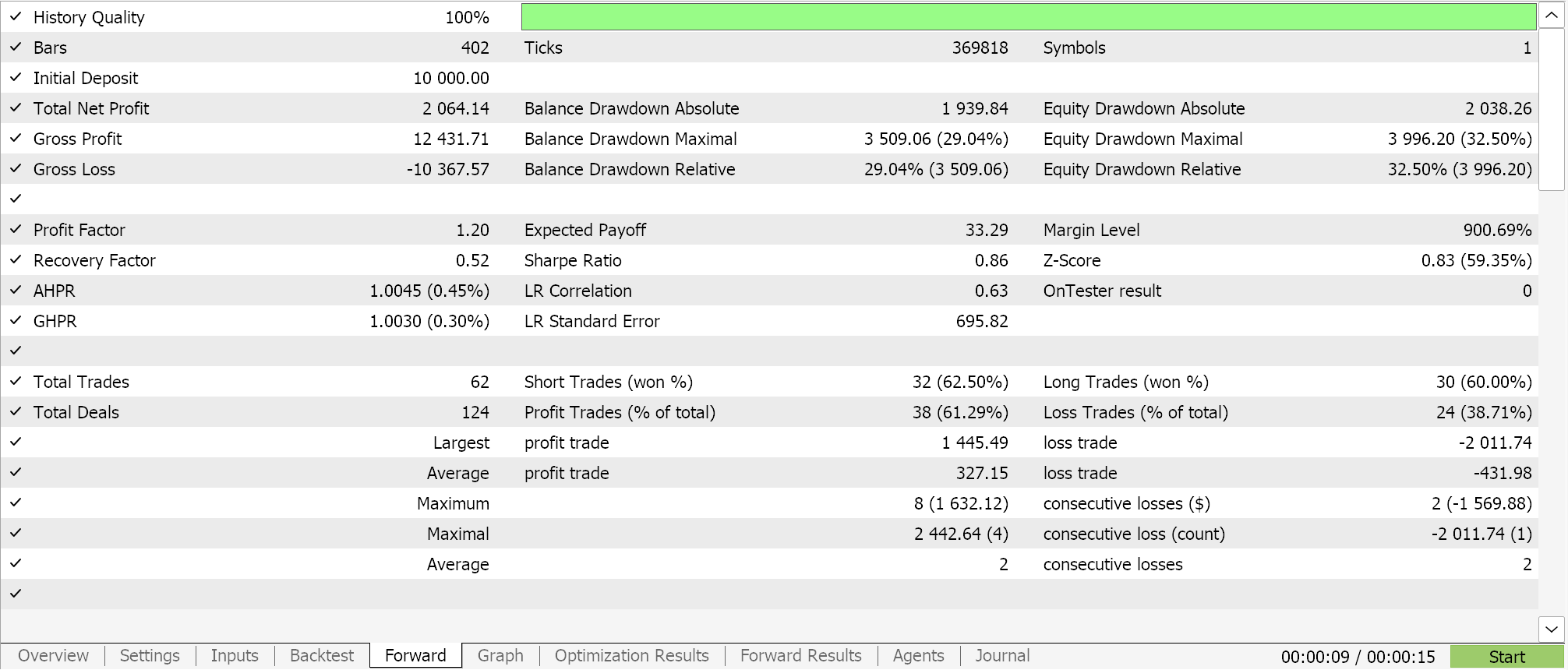
Ein vollständiger Durchlauf über das ganze Jahr ergibt dieses Salden-/Kapitalkurve

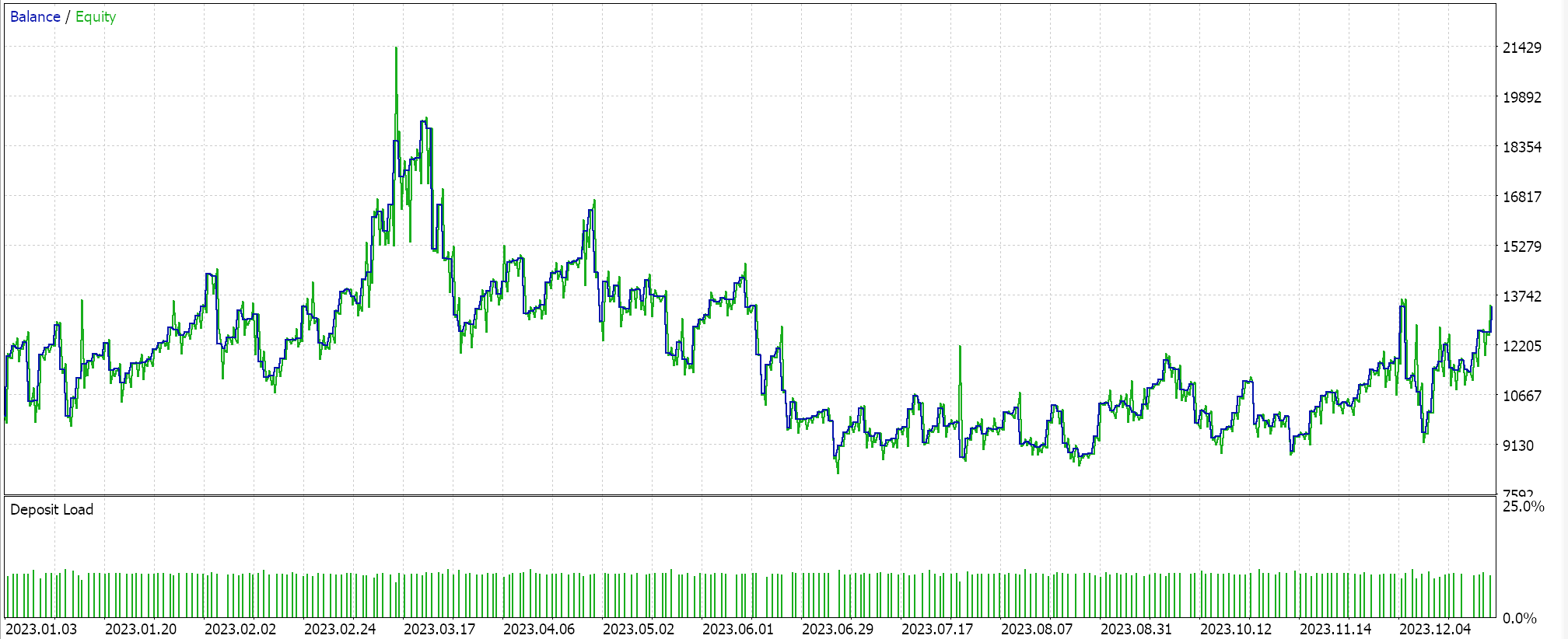
Trailing-Stop

Neben der Klasse der Expertensignale können wir mit dem Assistenten einen Expertenberater zusammenstellen, indem wir auch eine Methode zum Setzen und Anpassen des Trailing-Stops für offene Positionen auswählen. In der Bibliothek sind Methoden enthalten, die Parabolic Sar und gleitende Durchschnitte verwenden, aber insgesamt ist ihre Anzahl viel geringer als die der Signalbibliothek. Wenn wir diese Anzahl verbessern wollen, indem wir eine Klasse hinzufügen, die das Newtonsche Polynom verwendet, dann müssten unsere Stichprobendaten wohl Preisspannen sein.

Wenn wir also dieselben Schritte befolgen, die wir oben bei der Projektion des nächsten Schlusskurses unternommen haben, wobei die wichtigste Änderung die Daten für den y-Vektor sind, die in diesem Fall nun die Preisbalkenbereiche sind, dann würde unsere Quelle wie folgt aussehen:

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingNP::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

   ...

//---
   m_high.Refresh(-1);
   m_low.Refresh(-1);
   vector _x, _y;
   _x.Init(m_length);
   _y.Init(m_length);
   for(int i = 0; i < m_length; i++)
   {  _x[i] = i;
      _y[i] = (m_high.GetData(StartIndex()+i)-m_low.GetData(StartIndex()+i));
   }
   vector _w;
   _w.Init(m_length);
   _w[0] = _y[0];
   __N.Set(_w, _x, _y);
   double _xx = -1.0;
   double _yy = 0.0;
   __N.Get(_w, _x, _xx, _yy);
//---

   ...

//---
   return(sl != EMPTY_VALUE);
}

Ein Teil dieser prognostizierten Spanne wird dann verwendet, um die Größe des Stop-Loss der Position festzulegen. Der verwendete Anteil ist ein optimierbarer Parameter „m_stop_level“, und bevor der neue Stop-Loss gesetzt wird, addieren wir den minimalen Stop-Abstand zu diesem Delta, um Maklerfehler zu vermeiden. Diese Normalisierung wird durch den nachstehenden Code erfasst:

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingNP::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check
   
   ...

//---
   sl = EMPTY_VALUE;
   tp = EMPTY_VALUE;
   delta = (m_stop_level * _yy) + (m_symbol.Point() * m_symbol.StopsLevel());
//---
   if(price - base > delta)
   {  sl = price - delta;
   }
//---
   return(sl != EMPTY_VALUE);
}

Wenn wir mit dem MQL5-Assistenten einen Experten zusammenstellen, der die Signalklasse Awesome Oscillator aus der Bibliothek verwendet, und versuchen, nur für die ideale Polynomlänge zu optimieren, und zwar für dasselbe Symbol, denselben Zeitrahmen und dieselbe 1-Jahres-Periode wie oben, erhalten wir den folgenden Bericht als unseren besten Fall:

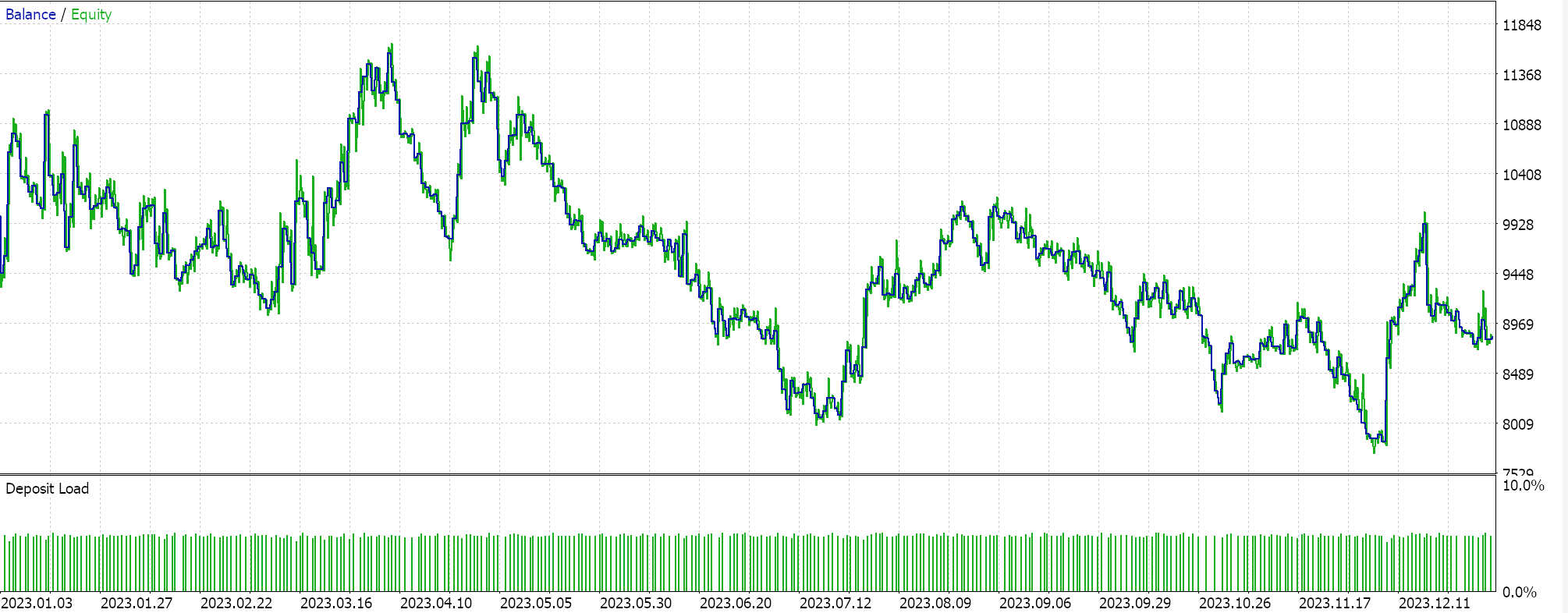
Die Ergebnisse sind bestenfalls mäßig. Interessanterweise erhalten wir bessere Ergebnisse, wenn wir zur Kontrolle denselben Expert Advisor mit einem auf dem gleitenden Durchschnitt basierenden Trailing-Stop verwenden, wie in den unten stehenden Berichten angegeben:

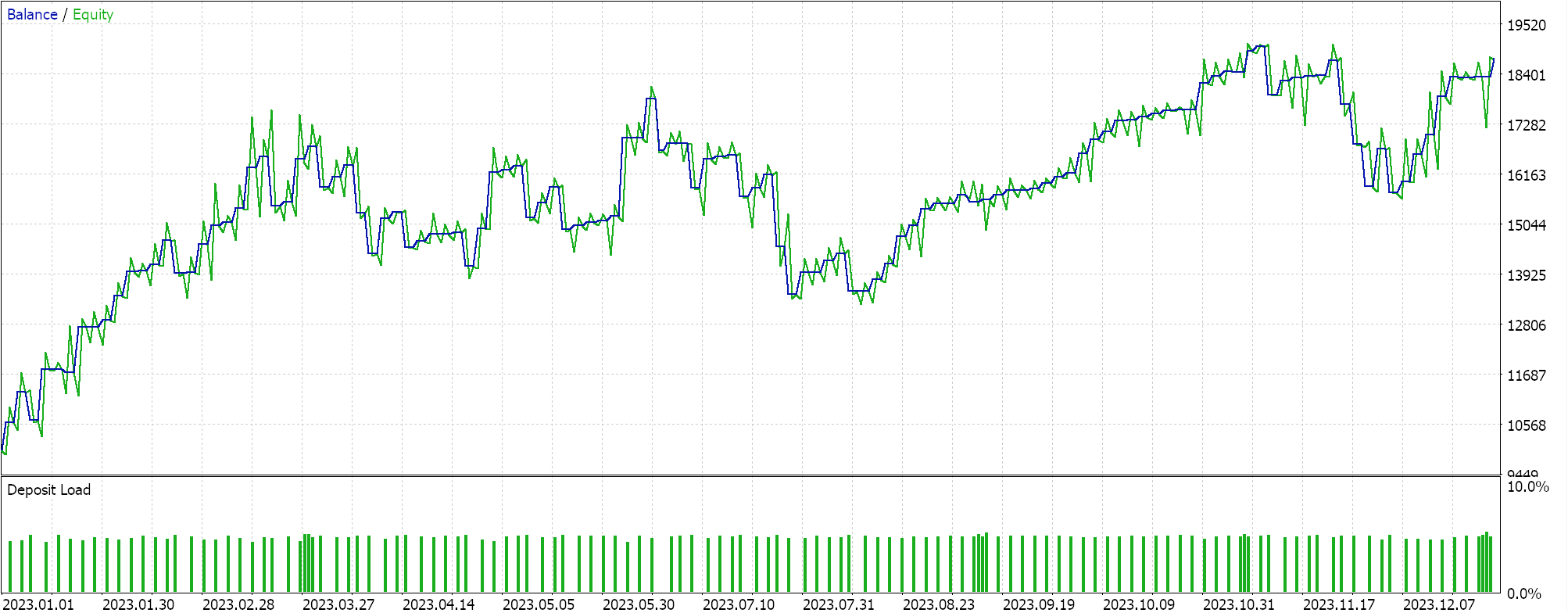
Diese besseren Ergebnisse können darauf zurückgeführt werden, dass mehr Parameter optimiert wurden als nur der eine, den wir mit dem Polynom hatten, und dass die Kopplung mit einem anderen Expertensignal zu völlig anderen Ergebnissen führen könnte. Für die Zwecke von Kontrollversuchen könnten diese Berichte jedoch als Leitfaden für das Potenzial des Newtonschen Polynoms bei der Verwaltung von Stop-Loss-Positionen dienen.

Geld-Management

Schließlich betrachten wir, wie Newton-Polynome bei der Positionsbestimmung helfen können, die von der dritten Art der eingebauten Assistenten-Klassen mit der Bezeichnung „CExpertMoney“ gehandhabt wird. Wie also könnte unser Polynom dabei helfen? Es gibt sicherlich viele Richtungen, die man einschlagen kann, um eine optimale Nutzung zu finden. Wir werden jedoch Änderungen in der Bar-Range als einen Indikator für die Volatilität und somit als einen Leitfaden für die Anpassung einer festen Margin-Positionsgröße betrachten. Unsere einfache These ist, dass wir, wenn wir eine steigende Preisspanne prognostizieren, unsere Position entsprechend verkleinern würden, aber wenn sie nicht steigt, dann tun wir nichts. Wir werden keine Erhöhungen aufgrund des prognostizierten Rückgangs der Volatilität haben.

Unser Quellcode, der uns dabei hilft, ist weiter unten zu finden, wobei die ähnlichen Teile wie die oben beschriebenen herausgearbeitet wurden.

//+------------------------------------------------------------------+
//| Optimizing lot size for open.                                    |
//+------------------------------------------------------------------+
double CMoneySizeOptimized::Optimize(double lots)
{  double lot = lots;
//--- 0 factor means no optimization
   if(m_decrease_factor > 0)
   {  m_high.Refresh(-1);
      m_low.Refresh(-1);
      vector _x, _y;
      _x.Init(m_length);
      _y.Init(m_length);
      for(int i = 0; i < m_length; i++)
      {  _x[i] = i;
         _y[i] = (m_high.GetData(StartIndex() + i) - m_low.GetData(StartIndex() + i)) - (m_high.GetData(StartIndex() + i + 1) - m_low.GetData(StartIndex() + i + 1));
      }
      vector _w;
      _w.Init(m_length);
      _w[0] = _y[0];
      __N.Set(_w, _x, _y);
      double _xx = -1.0;
      double _yy = 0.0;
      __N.Get(_w, _x, _xx, _yy);
      //---
      if(_yy > 0.0)
      {  double _range = (m_high.GetData(StartIndex()) - m_low.GetData(StartIndex()));
         _range += (m_decrease_factor*m_symbol.Point());
         _range += _yy;
         lot = NormalizeDouble(lot*(1.0-(_yy/_range)), 2);
      }
   }
//--- normalize and check limits

...

//---
   return(lot);
}

Noch einmal: Wenn wir die Optimierungen NUR für den polynomialen Rückblick auf einen Expertenberater ausführen, der dieselbe Signalklasse verwendet, die wir mit dem nachlaufenden Expertenberater für dasselbe Symbol, denselben Zeitrahmen und denselben Zeitraum hatten, erhalten wir die folgenden Berichte:

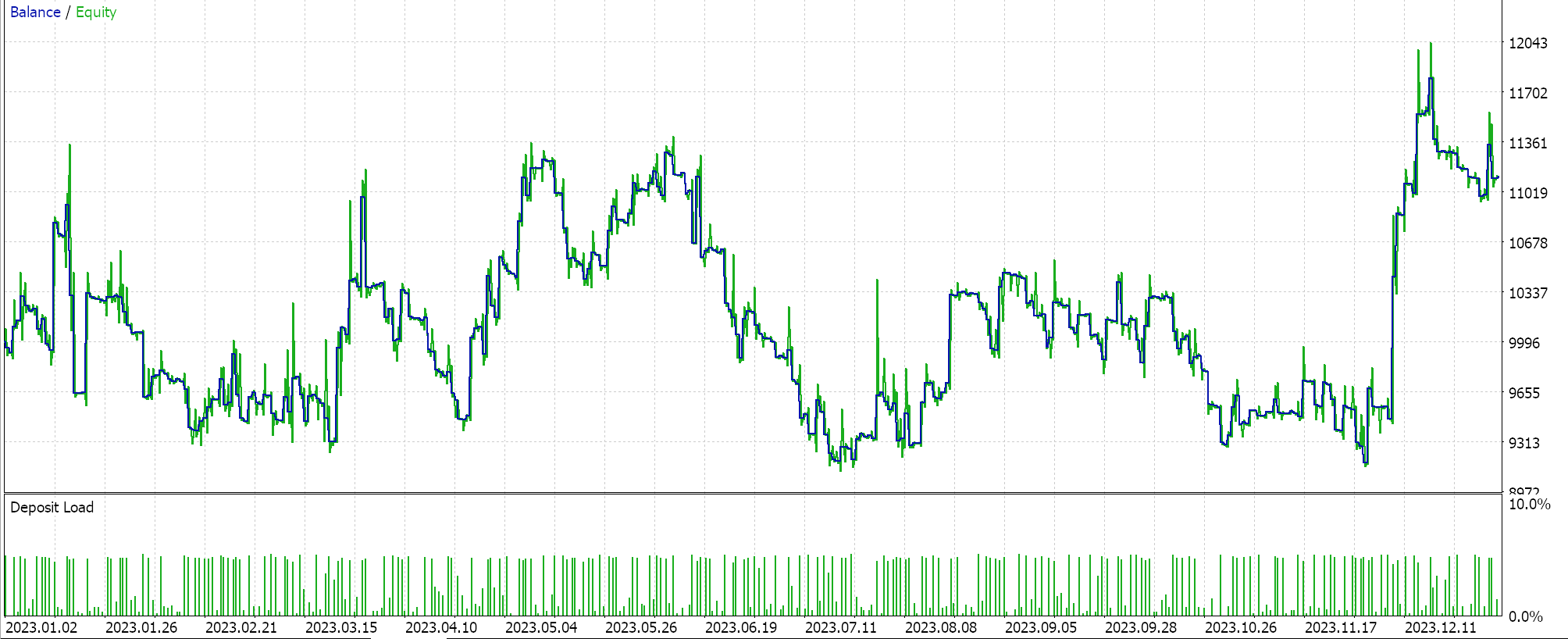
Bei diesem Expertenberater wurde im Assistenten keine Trailing-Stop-Methode ausgewählt, und er verwendet im Wesentlichen die Rohsignale des Awesome-Oszillators, wobei die einzigen Änderungen in der Verringerung der Positionsgröße bestehen, wenn Volatilität prognostiziert wird.

Zur Kontrolle verwenden wir die eingebaute „größenoptimierte“ Geldmanagementklasse auf einem Experten mit ähnlichem Signal und ebenfalls ohne Trailing-Stop. Dieser Experte erlaubt nur die Anpassung des Reduktionsfaktors, der einen Nenner für einen Bruch bildet, der die Positionsgröße im Verhältnis zu den vom Expertenberater erlittenen Verlusten reduziert. Wenn wir Tests mit den besten Einstellungen durchführen, erhalten wir die folgenden Berichte.

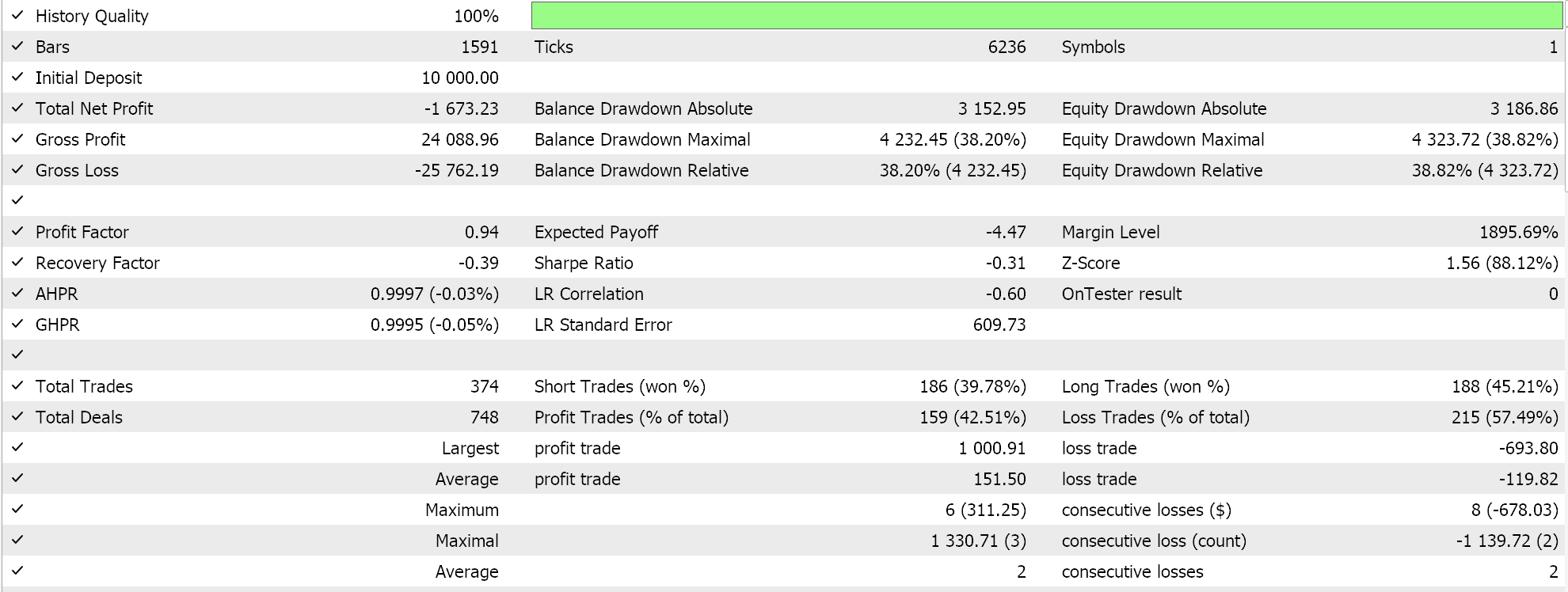
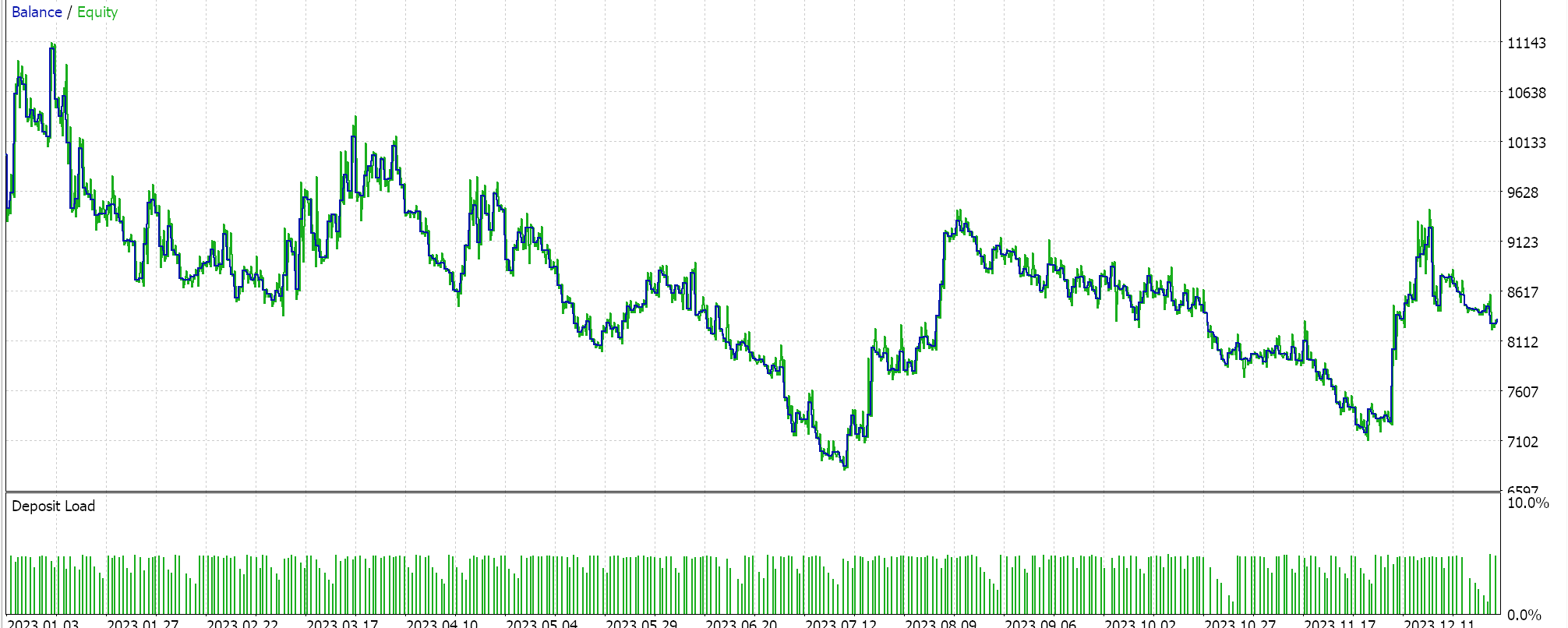
Die Ergebnisse sind eindeutig blass im Vergleich zu dem, was wir mit dem Newton-Polynom-Geldmanagement erreicht hatten, was wiederum, wie wir bei den Trailing-Klassen gesehen haben, nicht per se eine Anklage gegen positionsgrößenoptimierte Experten ist, aber für unsere Vergleichszwecke könnte es bedeuten, dass das Newton-Polynom-basierte Geldmanagement, so wie wir es implementiert haben, eine bessere Alternative ist.

Schlussfolgerung

Abschließend haben wir uns mit dem Newtonschen Polynom befasst, einer Methode, die aus einer Reihe von Datenpunkten eine Polynomgleichung ableitet. Dieses Polynom und die Zahlenwand, die im letzten Artikel betrachtet wurde, oder die eingeschränkte Boltzmann-Maschine davor stellen Einführungen in Ideen dar, die über das hinausgehen, was in dieser Serie betrachtet wird.

Es gibt eine entstehende Denkschule, die sich dafür ausspricht, bei der Analyse der Märkte an den bewährten Methoden festzuhalten, und diese Artikel sind nicht per se dagegen, aber wenn wir uns in einer Situation befinden, in der alles von BTC über Aktien bis hin zu Anleihen und sogar Rohstoffen ziemlich stark korreliert ist, könnte dies ein Vorbote für systemische Ereignisse sein? In Zeiten, in denen das Geld locker sitzt, ist es leicht, einen Vorteil zu vernachlässigen. Daher können diese Serien als Mittel betrachtet werden, um neue und oft ungeliebte Ansätze zu fördern, die eine dringend benötigte Absicherung bieten könnten, während wir alle ins Ungewisse waten.

Wie aus den obigen Testberichten hervorgeht, haben Newtons Polynome ihre Grenzen, die in erster Linie auf ihre Unfähigkeit zurückzuführen sind, weißes Rauschen herauszufiltern, was bedeutet, dass sie gut funktionieren können, wenn sie mit anderen Indikatoren kombiniert werden, die dieses Problem lösen. Der MQL5-Assistent ermöglicht die Verknüpfung mehrerer Signale zu einem einzigen Expertenratgeber, sodass ein Filter oder sogar mehrere Filter verwendet werden können, um ein besseres Expertensignal zu erhalten. Die Trailing-Klasse und die Money-Management-Module lassen dies nicht zu, sodass weitere Tests durchgeführt werden müssten, um herauszufinden, welche Trailing- und Money-Management-Klassen am besten mit dem Signal funktionieren.

Die Unfähigkeit, weißes Rauschen zu filtern, kann also auf die Tendenz von Polynomen zurückgeführt werden, sich zu sehr an die abgetasteten Daten anzupassen, indem sie alle Wiggles erfassen, anstatt die zugrunde liegenden Muster zu verarbeiten. Dies wird oft als „Erinnerungsrauschen“ bezeichnet und führt zu einer schlechten Leistung bei Daten, die nicht in der Stichprobe enthalten sind. Finanzielle Zeitreihen haben in der Regel auch wechselnde statistische Eigenschaften (Mittelwert, Varianz...) und eine nichtlineare Dynamik, bei der abrupte Preisänderungen die Norm sein können. Die Newtonschen Polynome, die auf glatten Polynomkurven basieren, können solche Feinheiten nur schwer erfassen. Da sie nicht in der Lage sind, wirtschaftliche Stimmungen und Fundamentaldaten zu berücksichtigen, sollten sie, wie oben erwähnt, mit geeigneten Finanzindikatoren kombiniert werden.