MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 11): Number Walls

Einführung

Für einige wenige Zeitreihen ist es möglich, eine Formel für den nächsten Wert in den Sequenzen zu entwickeln, die auf den vorhergehenden Werten basiert, die innerhalb der Sequenz auftraten. Number Walls, Zahlenwände, ermöglichen dies, indem im Vorfeld eine „Zahlenwand“ in Form einer Matrix über die so genannte Kreuzregel erzeugt wird. Bei der Erstellung dieser Matrix geht es in erster Linie darum, festzustellen, ob die betreffende Folge konvergent ist, und der Zahlenwand-Kreuzregel-Algorithmus beantwortet diese Frage gerne, wenn nach einigen Zeilen der Anwendung die nachfolgenden Zeilen in der Matrix nur noch Nullen sind.

In diesem veröffentlichen Artikel, das diese Konzepte aufzeigt, wurde die Laurent Power Series alias Formal Laurent Series (FLS) als Rahmen für die Darstellung dieser Sequenzen mit ihrer Arithmetik im Polynomformat unter Verwendung von Cauchy-Produkten verwendet.

Im Allgemeinen erfüllen LFSR-Sequenzen eine Rekursionsbeziehung, sodass die Linearkombination aufeinanderfolgender Terme immer Null ist, wie in der folgenden Gleichung dargestellt:

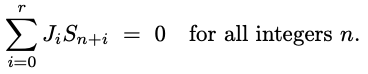
Wenn die Sequenz Sn ein linear wiederkehrendes oder linear rückgekoppeltes Schieberegister (linear feedback shift register, LFSR) ist und es einen Nicht-Null-Vektor |Ji| (die Beziehung) der Länge r + 1 gibt.

Dies impliziert eine Vektorbeziehung, deren Elemente die x-Koeffizienten (Konstanten sind Koeffizienten von x hoch Null) sind. Dieser Vektor hat per Definition einen Betrag von mindestens 2.

Um dies zu veranschaulichen, können wir einige einfache Beispiele betrachten, wobei das erste eine Folge von Kubikzahlen ist. Wir alle wissen, dass kubische Zahlen von Null an aufwärts aufgezählt werden, wobei jeder Wert ein Kubus seiner Indexposition ist; und wenn wir diese in eine Zahlenwandmatrix einspeisen würden, sähe die anfängliche Darstellung wie folgt aus:

Die Nullen und Einsen, die als Zeilen über der Sequenz angegeben sind, sind immer implizit und helfen bei der Anwendung der Kreuzregel, um alle fehlenden Werte innerhalb der Matrix zu übertragen. Bei der Anwendung der Kreuzregel sollte für alle 5 Werte in der Matrix, die ein einfaches Kreuzformat haben, das Produkt der äußeren vertikalen Werte, wenn es zum Produkt der äußeren horizontalen Werte addiert wird, immer dem Quadrat des Mittelwertes entsprechen.

Wendet man diese Regel auf die obige Grundfolge von Kubikzahlen an, erhält man die unten dargestellte Matrix:

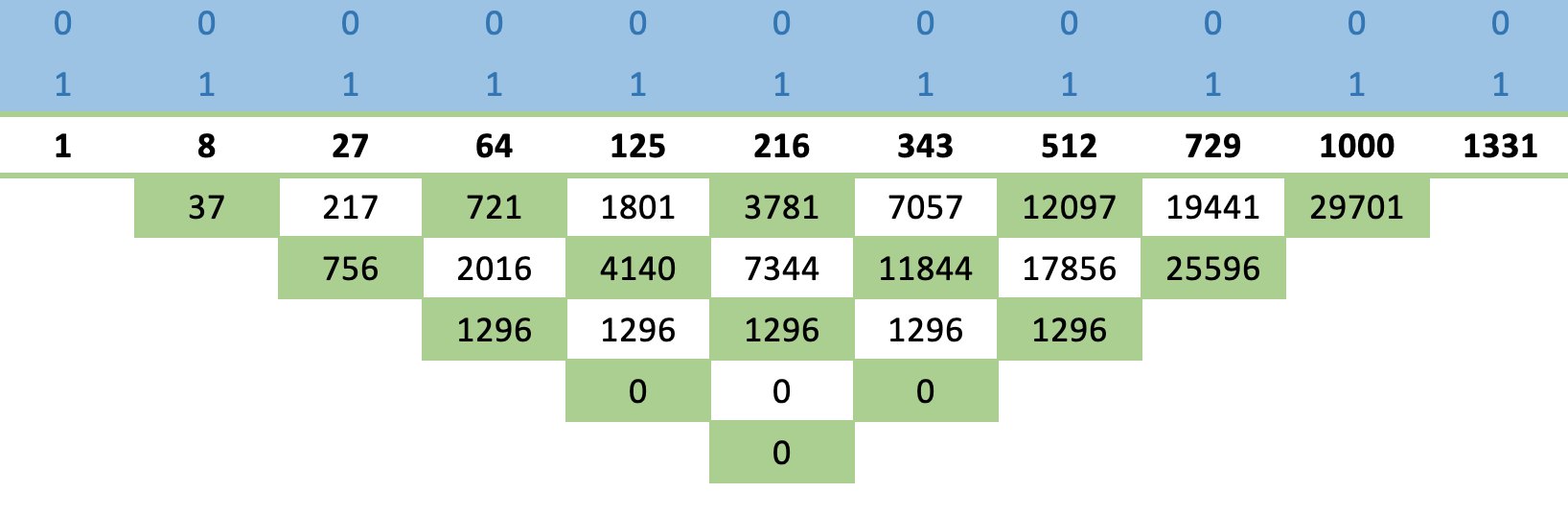
Um die Kreuzregel zu veranschaulichen: Die Zahl unter 216, also 3781, ergibt ich aus der Differenz des Quadrates von 216 und dem Produkt von 125 und 343, die durch die Zahl über 216, also 1, dividiert wird.

Die Tatsache, dass wir in der Lage sind, so schnell Zeilen mit Nullen zu erhalten, signalisiert, dass diese Folge tatsächlich konvergent ist, und eine Formel für ihre nachfolgenden Werte kann leicht abgeleitet werden.

Doch bevor wir uns mit Formeln befassen, wollen wir ein weiteres Beispiel betrachten, die Fibonacci-Reihe. Wenn wir diese Folge in unserer Matrix anwenden und die lange Kreuzregel wie oben anwenden, erhalten wir die Zeilen mit Nullen noch schneller!

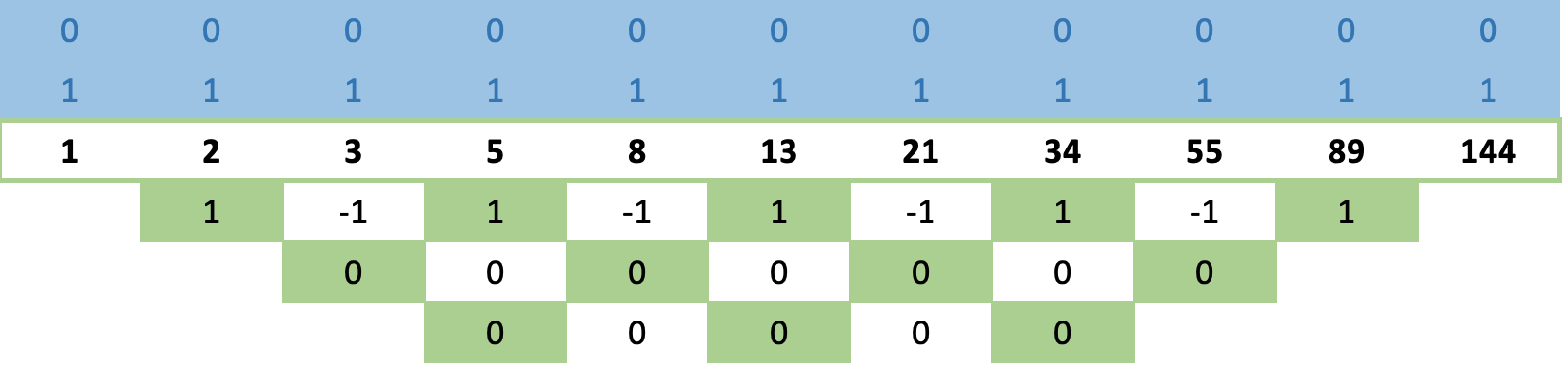
Dies erscheint sicherlich seltsam, da man erwarten würde, dass die Fibonacci-Reihe komplexer ist als kubische Zahlen und daher länger braucht, um zu konvergieren, aber nein! sie konvergiert bereits in der 2. Zeile.

Um die Formulierung einer konvergenten Reihe, wie die beiden oben betrachteten Beispiele, abzuleiten, würden wir innerhalb der Zahlenwandmatrix die Folge durch ein formelhaftes Format ersetzen, das jeden Wert in der Folge durch denselben Wert minus den mit x multiplizierten vorherigen Wert ersetzt. Dies sieht folgendermaßen aus:

Von hier aus wenden wir einfach unsere Kreuzregel an, wie wir es mit den obigen Sequenzen getan haben, und erzeugen polynomial formatierte Werte für die folgenden Zeilen. Interessanterweise können wir bei einer konvergenten Folge auch mit den Polynomwerten nach einigen Durchläufen der langen Kreuzregel immer noch Zeilen mit Nullen erhalten. Dies wird im Folgenden anhand der Fibonacci-Folge veranschaulicht.

Was machen wir dann mit diesen polynomischen Werten? Nun, es stellt sich heraus, dass, wenn wir die letzte Gleichung mit 0 gleichsetzen und für die höchste Potenz von x lösen, die x-Koeffizienten, die wir auf der gegenüberliegenden Seite übrig haben, Vielfache für vorherige Werte in der Folge sind, die sich zum nächsten Wert summieren.

Mit der letzten Gleichung, die wir für die Fibonacci-Folge erhalten haben, können wir also die höchste Potenz von x^2 bestimmen, die uns bleibt: 1 + x ;

Denken Sie daran, dass die 1 für x^0 steht und im Grunde ein Koeffizient für die Sequenznummer vor der Sequenznummer ist, deren Koeffizient x ist. Im Klartext bedeutet dies, dass in einer Fibonacci-Reihe jede Zahl die Summe zweier vorheriger Zahlen in der Folge ist.

Wie sieht die Polynomgleichung für die kubische Folge aus? Es braucht mehr Zeilen, um zu konvergieren, wie oben gezeigt, und ist daher komplexer, als wenn man die Gleichung als Würfel ausdrücken würde, was man erwarten würde.

Wie sieht es mit nicht konvergenten Reihen aus, welche Art von Matrizen würde man in diesen Szenarien erzeugen? Um dies zu veranschaulichen, könnten wir uns die Kursfolge eines regulären Devisenpaares ansehen, zum Beispiel EURUSD. Wenn wir versuchen, eine Zahlenwandmatrix (ohne die Formel) zu generieren, um die Konvergenz an einer Folge von EURUSD-Tagesschlusskursen für die ersten 5 Handelstage des Jahres 2024 zu testen, würden wir eine Wand erhalten, die für die ersten 5 Zeilen etwa so aussieht.

Es versteht sich von selbst, dass wir innerhalb der ersten Zeilen keine Konvergenz erhalten, und es ist bei weitem nicht klar, ob wir jemals streng konvergent werden, obwohl der Trend der Wand gegen Null geht, was beruhigend sein sollte. Dies beeinträchtigt die Anwendbarkeit von Zahlenwänden für unsere Zwecke, und in der Tat ist dieser Vorprüfungsprozess in der Regel auch rechenintensiv, und hier kommt die Toeplitz-Matrix ins Spiel.

Wenn wir eine Matrix erstellen, bei der alle Zeilen auf irgendeine Weise miteinander in Beziehung stehen, indem wir eine gleitende Wiederholung der Sequenzzeile verwenden, ist die Determinante dieser Matrix gleich Null, wenn die Sequenz konvergent ist. Dies ist eine recheneffizientere Methode, um auf Konvergenz zu testen, und darüber hinaus gibt sie an, wie hoch die Wahrscheinlichkeit ist, dass eine Sequenz konvergiert, basierend auf der Größe der Determinante.

Wir könnten also die Kreuzregel auf der Formelmatrix auf eine beliebige Sequenz übertragen und die Größe der Determinante verwenden, um den Prognosewert der Formel „abzuzinsen“. Alternativ können wir einen absoluten Schwellenwert für die Determinante festlegen, bei dessen Überschreitung wir das Ergebnis unserer Formel ignorieren.

All dies sind mögliche Lösungen für nicht-konvergente Finanz- und andere Zeitreihen und sie sind sicherlich nicht perfekt, aber lassen Sie uns untersuchen, welches Potenzial sie haben, wenn sie in MQL5 implementiert sind.

MQL5-Implementierung

Um diese Ideen in MQL5 zu veranschaulichen, werden wir sie in einer Instanz der Expert Trailing-Klasse implementieren, die mit der integrierten Awesome Oscillator-Klasse gepaart ist, um einen einfachen Expert Advisor zu erstellen. Die Instanz der Trailing-Klasse verwendet die Zahlenwand, um die Größe des Trailing-Stop-Loss- und Take-Profit-Levels zu bestimmen.

Bei der Implementierung mit MQL5 werden wir die integrierten Datentypen Matrix und Vektor aufgrund ihrer zusätzlichen Funktionen und minimalen Codeanforderungen häufig verwenden. Wir können eine Sequenz auf Konvergenz überprüfen, indem wir eine typische (nicht formelhafte) Zahlenwand aufbauen und prüfen, ob wir eine Zeile mit Nullen erhalten, aber angesichts der Art und Komplexität von Finanzzeitreihen ist es eine Selbstverständlichkeit, dass die Matrix nicht konvergiert, und daher ist es besser, die Formel für den nächsten Wert in der Sequenz zu berechnen, wie sie sich aus der untersten Zeile der letzten Spalte nach der Fortentwicklung ergibt.

Zur Erstellung der Wand verwenden wir Vektoren, um Koeffizienten in x zu speichern. Die Multiplikation zweier solcher Vektoren bei der Lösung der unbekannten Zeile wäre gleichbedeutend mit einer Kreuzkorrelation, da die resultierenden Vektorwerte die x-Koeffizienten wären, wobei eine höhere Indexierung einen höheren Exponenten für x bedeutet. Dies ist eine integrierte Funktion, aber wenn es um die Division geht, müssen wir die Größe der beiden Quotientenvektoren ändern, um sicherzustellen, dass sie übereinstimmen, wobei ein Größenunterschied einfach bedeutet, dass sie nicht in x Exponenten übereinstimmen.

Um zu bestimmen, um wie viel die offene Position TP und SL angepasst werden soll, werden die Indikatorwerte des gleitenden Durchschnitts als Eingangssequenz für unsere Zahlenwand verwendet. Jeder Indikator kann verwendet werden, obwohl dieser oder ein Bollinger-Band- oder ein Envelope-Indikator für die Anpassung des Trailing-Stops besser geeignet sein könnte.

MQL5-Vektoren können problemlos Indikatorwerte kopieren und laden, sobald ein Handle definiert ist. Sehen wir uns den nachstehenden Quellcode für einen typischen Check-Trailing-Stop-Code an (der sowohl für Kauf- als auch für Verkaufspositionen verwendet werden kann)

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingLFSR::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

...

//---
   vector _t, _p;
   _p.Init(2);
   _t.CopyIndicatorBuffer(m_ma.Handle(), 0, 0, 2);
   double _s = 0.0;
   for(int i = 1; i >= 0; i--)
   {  _s = 0.0;
      _p[i] = GetOutput(i, _s);
   }
   double _o = SetOutput(_t, _p);
//---
  
...

}

Wir sehen, dass sich unsere Entscheidungsfindung um zwei Funktionen herum entwickelt, nämlich um „get output“ und „set output“. Die Ausgabe von get ist die wichtigste, da sie die Zahlenwand aufbaut und Polynomkoeffizienten für eine Gleichung liefert, die den nächsten Wert in der Folge löst. Die get-Ausgabe wird wie unten angegeben aufgelistet:

//+------------------------------------------------------------------+
//| LFSR Output.                                                     |
//+------------------------------------------------------------------+
double CTrailingLFSR::GetOutput(int Index, double &Solution)
{  double _output = 0.0;
   vector _v;
   _v.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   Solution = Solvability(_v);
   _v.Resize(m_length + 1);
   for(int i = 2; i < 2 + m_length; i++)
   {  for(int ii = 2; ii < 2 + m_length; ii++)
      {  if(i == 2)
         {  vector _vi;
            _vi.Init(1);
            _vi[0] = _v[m_length - ii + 1];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(i == 3)
         {  vector _vi;
            _vi.Init(2);
            _vi[0] = m_numberwall.row[i - 1].column[ii][0];
            _vi[1] = -1.0 * m_numberwall.row[i - 1].column[ii - 1][0];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(ii < m_length + 1)
         {  m_numberwall.row[i].column[ii] = Get(m_numberwall.row[i - 2].column[ii], m_numberwall.row[i - 1].column[ii - 1], m_numberwall.row[i - 1].column[ii + 1], m_numberwall.row[i - 1].column[ii]);
         }
      }
   }
   vector _u = Set();
   vector _x;
   _x.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   _u.Resize(fmax(_u.Size(),_x.Size()));
   _x.Resize(fmax(_u.Size(),_x.Size()));
   vector _y = _u * _x;
   _output = _y.Sum();
   return(_output);
}

Unsere gemeinsame Auflistung oben ist grundsätzlich 2-teilig. Bauen wir die Wand, um die Koeffizienten der Gleichung unter Verwendung der Gleichung mit den aktuellen Sequenzmesswerten zur Projektion zu erhalten. Im ersten Teil ist die Funktion get der Schlüssel zum Multiplizieren der erzeugten Gleichungen und zum Lösen der Gleichung für die nächste Zeile. Die Liste ist nachstehend aufgeführt:

//+------------------------------------------------------------------+
//| Get known Value                                                  |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Get(vector &Top, vector &Left, vector &Right, vector &Center)
{  vector _cc, _lr, _cc_lr, _i_top;
   _cc = Center.Correlate(Center, VECTOR_CONVOLVE_FULL);
   _lr = Left.Correlate(Right, VECTOR_CONVOLVE_FULL);
   ulong _size = fmax(_cc.Size(), _lr.Size());
   _cc_lr.Init(_size);
   _cc.Resize(_size);
   _lr.Resize(_size);
   _cc_lr = _cc - _lr;
   _i_top = 1.0 / Top;
   vector _bottom = _cc_lr.Correlate(_i_top, VECTOR_CONVOLVE_FULL);
   return(_bottom);
}

Ebenso verwendet die Funktion set den untersten Vektor, der die zuletzt übertragenen Koeffizienten enthält, um den nächsten Sequenzwert zu ermitteln; die Auflistung ist unten zu finden:

//+------------------------------------------------------------------+
//| Set Unknown Value                                                |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Set()
{  vector _formula = m_numberwall.row[m_length + 1].column[m_length + 1];
   vector _right;
   _right.Copy(_formula);
   _right.Resize(ulong(fmax(_formula.Size() - 1, 1.0)));
   double _solver = -1.0 * _formula[int(_formula.Size() - 1)];
   if(_solver != 0.0)
   {  _right /= _solver;
   }
   return(_right);
}

Innerhalb einer Check-Trailing-Funktion rufen wir die Get-Output-Funktion zweimal auf, da wir nicht nur die aktuelle Prognose, sondern auch die vorherige erhalten müssen, um die Normalisierung unserer Ausgaben zu unterstützen, da die meisten Sequenzen und insbesondere Finanzzeitreihen nicht konvergieren (wie in der Einleitung erwähnt). Es ist nicht ungewöhnlich, sehr große Werte zu erhalten, die um mehrere Größenordnungen über den typischen Sequenzwerten liegen, oder sogar einen negativen Wert, wenn offensichtlich nur positive Werte erwartet werden.

Bei der Normalisierung verwenden wir also eine sehr kurze und einfache Ausgabefunktion, die im Folgenden beschrieben wird:

//+------------------------------------------------------------------+
//| Normalising Output to match Indicator Value                      |
//+------------------------------------------------------------------+
double CTrailingLFSR::SetOutput(vector &True, vector &Predicted)
{  return(True[1] - ((True[0] - True[1]) * ((Predicted[0] - Predicted[1]) / fmax(m_symbol.Point(), fabs(Predicted[0]) + fabs(Predicted[1])))));
}

Wir normalisieren lediglich den projizierten Wert, damit seine Größe innerhalb des Bereichs der Sequenzwerte liegt, und wir erreichen dies, indem wir Sequenzänderungen sowohl für den vorhergesagten als auch für den wirklichen Wert verwenden.

Außerdem messen wir bei der typischen Überprüfung des Trailing-Stops die Lösbarkeit innerhalb der Get-Output-Funktion an ihrem Anfang. Diese Metrik wird als Schwellenwertfilter verwendet, um festzustellen, ob wir die Vorhersage ignorieren sollten, wobei die These lautet, dass größere Determinantenwerte (die wir als Lösbarkeit bezeichnen) auf eine größere Unfähigkeit zur Konvergenz hinweisen. Es genügt zu sagen, dass auch eine Matrix mit einer kleinen Determinante nicht konvergiert, aber wir nehmen an, dass sie eher konvergiert, wenn sie mit mehr Zeilen zum Aufbau der Zahlenwand versehen ist, als eine Matrix mit einer höheren Determinante.

Wenn man dies alles zusammennimmt, erhält man die Instanz der Trailing-Klasse, die am Ende des Artikels angehängt ist, und obwohl vorläufige Tests darauf hindeuten, dass sie rechenintensiv ist, stellt sie meiner Meinung nach eine Idee dar, die verfeinert und sogar mit verschiedenen Strategien gepaart werden könnte, um ein robusteres Handelssystem zu entwickeln.

Der beigefügte Code zur Trailing-Klasse in MQL5 kann mit einem Assistenten leicht zusammengesetzt werden, um eine Vielzahl von Expert Advisors je nach Wahl der Signalklasse und des Money Managements zu erstellen. Wie immer finden Sie hier eine Anleitung, wie Sie vorgehen können.

Zusätzliche Hinweise

Bei den bis hierher betrachteten Zahlenwänden im gemeinsamen Code und den obigen Abbildungen wurden ganze Wertpapierkurse verwendet, die keine Nullen enthielten. Wenn wir beispielsweise Änderungen des Wertpapierpreises und nicht nur des Rohpreises prognostizieren wollen, würden wir idealerweise eine Inputreihe von Preisänderungen haben. Sobald wir anfangen, uns mit Veränderungen im Gegensatz zum absoluten Preis zu befassen, stoßen wir nicht nur auf negative Werte, sondern können auch einige Nullen haben, und das wird nicht selten der Fall sein.

Auf den ersten Blick mögen Nullen harmlos erscheinen, aber beim Aufbau von Zahlenwände stellen sie eine Herausforderung bei der Bestimmung der Werte in der nächsten Zeile dar. Betrachten Sie das folgende Beispiel:

Mit unserer grundlegenden Kreuzregel zum Lösen eines unbekannten Wertes stoßen wir auf ein Problem, da ein bekannter Wert gleich Null ist und wir daher bei der Multiplikation mit unserer Unbekannten mit leeren Händen dastehen. Um dies zu umgehen, bietet sich die Log-Cross-Regel an. Und hier ist seine Darstellung, wenn wir das Bild oben erweitern:

Wir können mit einiger Sicherheit die Null über unserer aktuellen Zeile umgehen, indem wir die folgende Formel anwenden:

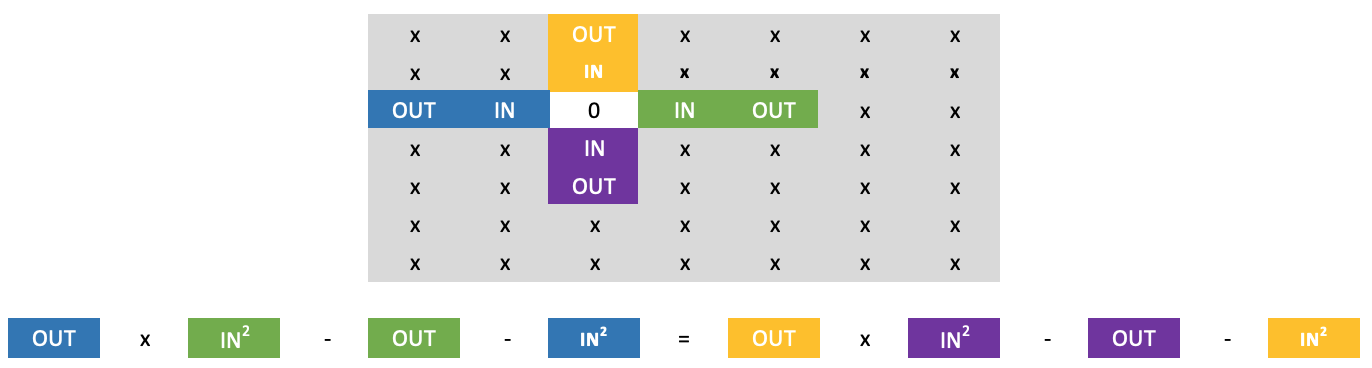
Ich erwähne das mit „einigem Vertrauen“, weil Zahlenwände eine ganz besondere Eigenschaft haben, wenn es darum geht, Nullen einzuschließen. Es stellt sich heraus, dass in jeder Zahl, die Nullen enthält, diese entweder einzeln oder in quadratischer Form vorkommen, d. h. sie können 1 x 1 (einzeln) oder 2 x 2 oder 3 x 3 usw. sein. Das heißt, wenn wir in einer beliebigen Zeile zwischen zwei Zahlen eine Null finden, ist die darunter liegende Zahl keine Null. Jeder kann jedoch sehen, dass wir bei Anwendung der Regel des langen Kreuzes eine zusätzliche Unbekannte in Form des niedrigsten äußeren Wertes in der Wand haben. Dies ist jedoch kein Problem, da sie mit unserer bekannten Null multipliziert wird, wodurch wir die Gleichung lösen können, ohne ihren Wert eingeben zu müssen.

Das Problem, auf das die Regel des langen Kreuzes abzielt, gilt ausschließlich für konvergierende Zahlenwände, und wie wir in den obigen Abbildungen gesehen haben, ist dies bei finanziellen Zeitreihen nur selten der Fall. Sollte dies also in Betracht gezogen werden? Dies sollte ehrlich gesagt für jede einzelne Sequenz festgelegt werden, je nachdem, auf welche Zeitreihe ein Handelssystem ausgerichtet ist. Einige könnten sich dafür entscheiden, es auch auf Finanzreihen anzuwenden, wenn die „Lösbarkeit“ oder die Determinante der Toeplitz-Matrix einen notwendigen Schwellenwert erreicht, andere könnten den Bau der Wand beenden und mit den Vektorkoeffizienten arbeiten, die sie zu diesem Zeitpunkt haben (wenn sie auf Nullen stoßen), um die Polynomgleichung für die Prognose zu erstellen. Es gibt diese und vielleicht noch ein paar andere Optionen, und die Wahl wird vom jeweiligen Händler abhängen.

Die lange Kreuzregel ist einfallsreich, wenn man bei der Fortpflanzung einer Zahlenwand nur auf eine Null stößt. Befinden sich die Nullen jedoch in einem größeren Quadrat (da Nullen in einer Wand immer das Format n x n einnehmen), dann wäre sie nicht von großem Nutzen, und in diesen Fällen wird oft die Hufeisenregel in Betracht gezogen. Bei dieser Regel werden die Werte der an dieses Quadrat angrenzenden Sequenzen um einen bestimmten Faktor skaliert, sobald ein großes Quadrat mit Nullen entsteht.

Diese vier Faktoren, einer für jede Seite eines Quadrats, haben eine einzigartige Eigenschaft, die sich mit der folgenden Formel zusammenfassen lässt:

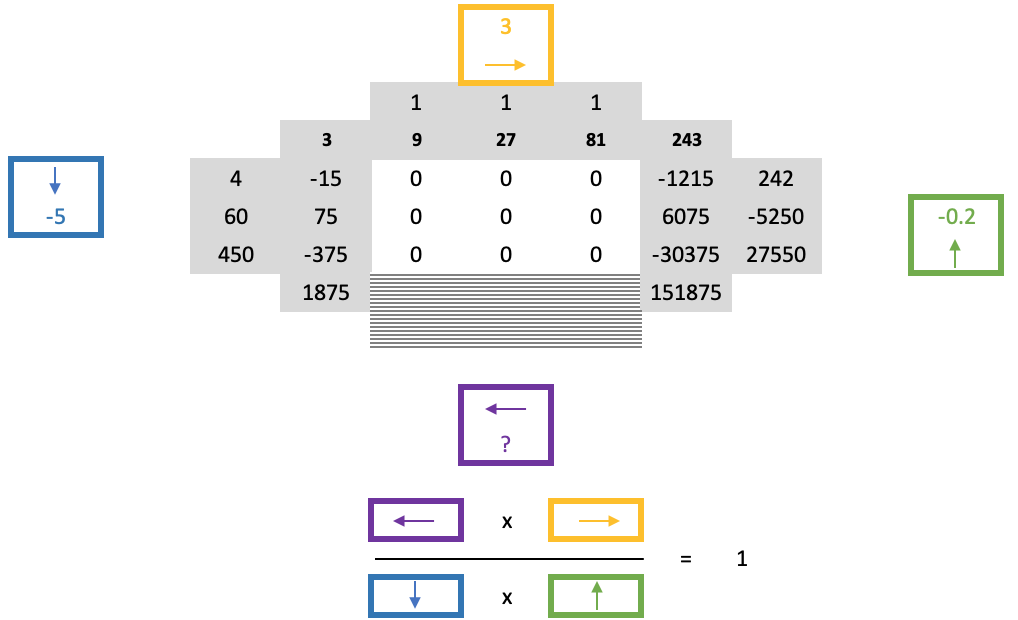
Wenn also eine große Tranche von Nullen auftritt, sind die oberen und seitlichen Zahlen, die diese Nullen begrenzen, bereits bekannt, und da wir die Breite der Nullenquadrate kennen, kennen wir im Wesentlichen auch ihre Höhe, was bedeutet, dass wir wissen, wo wir die unbekannten Grenzwerte bewerten müssen. Aus der obigen Gleichung lassen sich die unmittelbaren Grenzwerte unten ableiten, indem man den unteren Skalierungsfaktor ausrechnet und seine Zahlen berechnet, normalerweise von links nach rechts.

Von diesem Punkt aus mit der gewöhnlichen Kreuzregel fortzufahren, wäre jedoch immer noch schwierig, da die Nullen im Quadrat die Anwendung der Regel bei der Bestimmung der Zeile unterhalb der gerade gelösten Grenzreihe erschweren. Die Lösung dieses Problems ist der „zweite Teil“ der Hufeisenregel und beruht auf der folgenden, etwas langatmigen Formel:

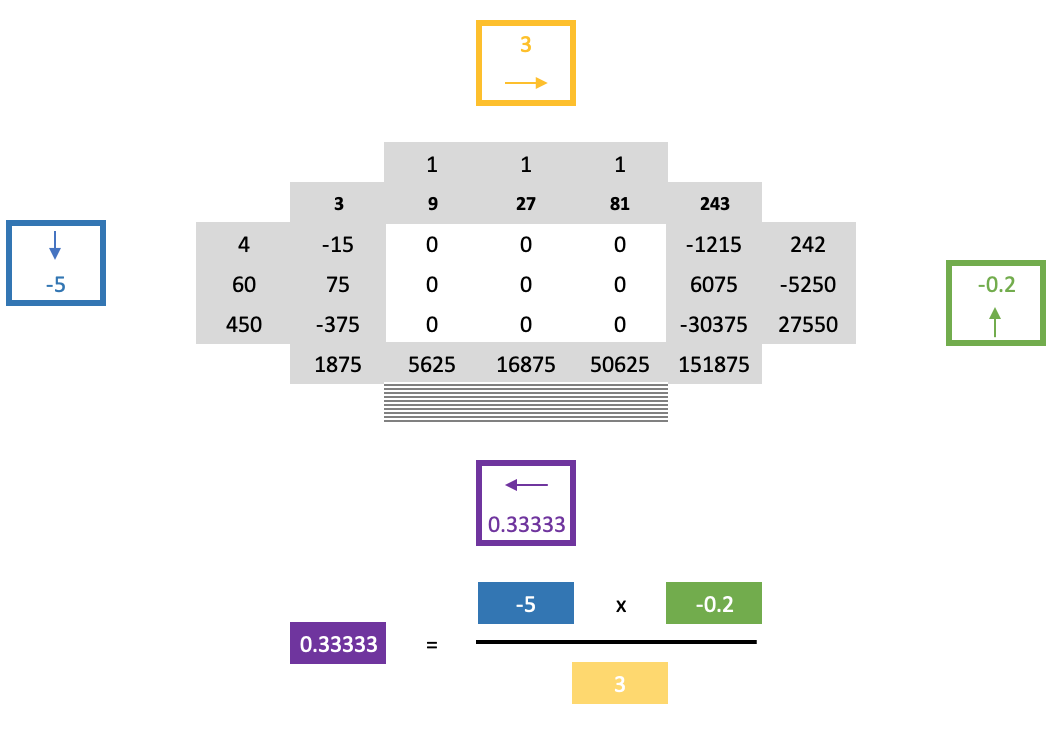
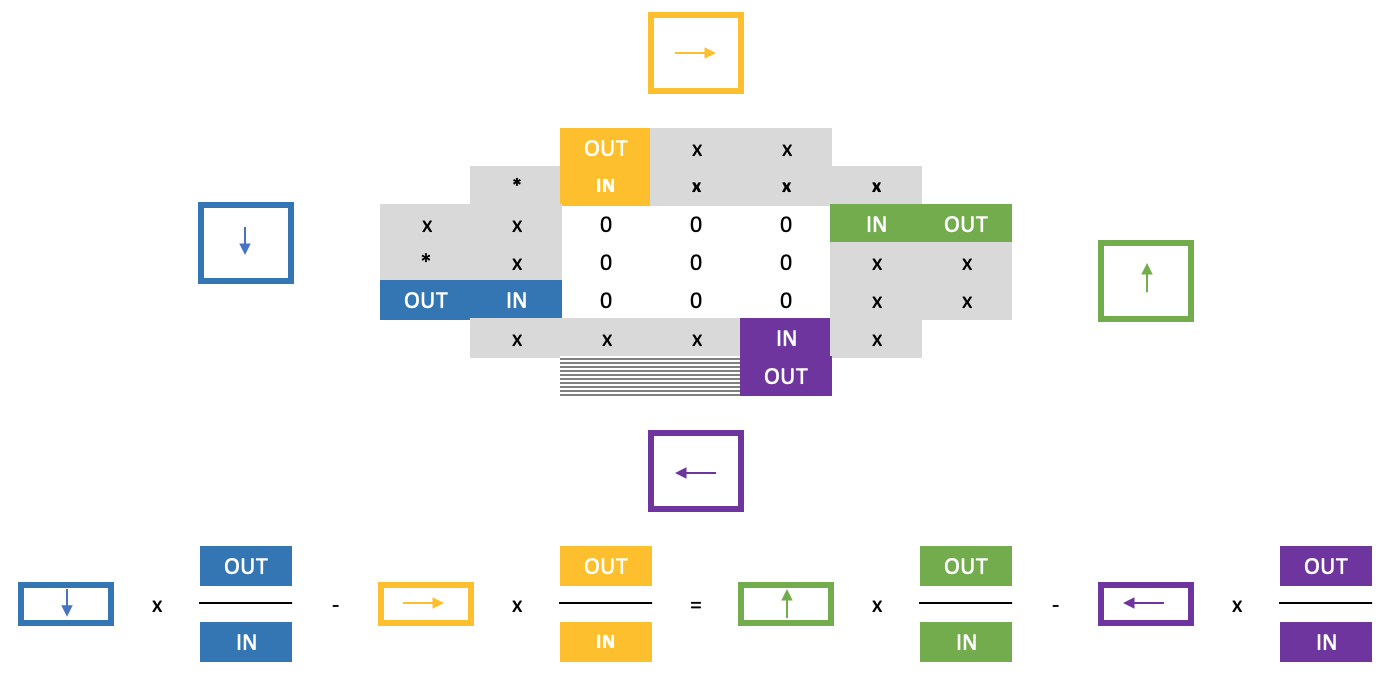
Das bereits oben erwähnte Papier zu diesem Thema hebt nicht nur viele der hier genannten Punkte hervor, sondern spricht auch ein wenig über die Pagodenvermutung. In seiner einfachsten Form ist dies die Summierung einer Gruppe von Zahlenmengen, wobei jede enthaltene Menge gleich groß ist, sodass, wenn jede der eingeschlossenen Mengen als ein Polygon konstruiert wird, bei dem jeder Scheitelpunkt eine der Zahlen in seiner Menge darstellt, diese Polygone zusammengeklebt werden können, um ein größeres komplexes Gitter zu bilden, mit der Bedingung, dass an jedem verbundenen Scheitelpunkt alle Polygonscheitelpunkte die gleiche Zahl haben. Dies geschieht natürlich unter der Bedingung, dass jede Scheitelpunktnummer auf einem beliebigen Polygon innerhalb dieser Menge eindeutig ist.

Dies hat erstens interessante pittoreske Konsequenzen für 3-Zahlenmengen, die eine Pagode bilden, da sich herausstellt, dass, wenn die Zahlen jeder Menge in einer Sequenz überlagert werden, sehr interessante sich wiederholende Muster in der sich ausbreitenden Zahlenwand beobachtet werden können, und das Papier zeigt einige dieser Bilder.

Für Handelszwecke stellt dieser „neuartige“ Klassifizierungsansatz jedoch eine weitere Möglichkeit dar, Finanzzeitreihen zu betrachten, die, um ehrlich zu sein, einen eigenständigen Artikel erfordern sollte, aber es genügt zu sagen, dass wir einige Möglichkeiten verallgemeinern können, wie wir Pagodensequenzen für unsere Zwecke einsetzen können.

Aus dem Stegreif könnte es ratsam sein, sich auf dreieckige Pagoden zu beschränken und nicht auf Formen mit höheren Dimensionen, da diese in der Regel mehr Möglichkeiten bieten und daher komplexer sind, wie sie zusammengefügt werden können. Wenn wir dies akzeptieren könnten, dann bestünde unsere Aufgabe erstens darin, unsere Finanzreihen zu normalisieren, um die Wiederholung von Werten zu berücksichtigen, die, wie bereits hervorgehoben, eine Voraussetzung für die Definition der Pagoden ist, und das Ausmaß, in dem diese Normalisierung vorgenommen wird, müsste sorgfältig geprüft werden, da verschiedene Iterationen zwangsläufig zu unterschiedlichen Ergebnissen führen.

Zweitens müssen wir, sobald wir mit einem bestimmten Normalisierungsschwellenwert zufrieden sind, die Anzahl der Dreiecke in unserer Pagode, d. h. die Gruppengröße, festlegen. Beachten Sie, dass mit zunehmender Größe der Gruppe die Notwendigkeit, alle Dreiecke direkt miteinander zu verbinden, abnimmt. So sind in einer Pagode mit 3 Dreiecken alle Dreiecke miteinander verbunden, aber mit zunehmender Zahl der Dreiecke kann jedes Dreieck höchstens 3 Verbindungen haben, was bedeutet, dass in einer Pagode mit 6 Dreiecken nur das unterste Dreieck in der Mitte Verbindungen an allen Ecken hat und alle anderen Dreiecke nur an zwei Ecken Verbindungen haben.

Diese zunehmende Komplexität bei der Verbindung der Dreiecke mit zunehmender Gruppengröße könnte darauf hindeuten, dass die Bestimmung der optimalen Gruppengröße zusammen mit der Festlegung des Normalisierungsschwellenwerts erfolgen sollte, da letzterer uns unsere wiederholten Daten liefert, die für die Erstellung der Verbindungen zwischen den Dreiecken entscheidend sind.

Schlussfolgerung

Um abzuschließen, wir haben uns mit Number Walls, den Zahlenwänden, beschäftigt, einem Zahlenraster, das aus einer untersuchten Sequenzzeitreihe generiert wird, und gesehen, wie es bei der Vorhersage durch die richtige Einstellung der offenen Position TP & SL im gemeinsamen Codebeispiel verwendet werden kann. Darüber hinaus haben wir uns mit dem verwandten Konzept der Pagodenvermutungen befasst, die in einem Aufsatz über Zahlenwände im Mittelpunkt standen, und einige Ideen vorgelegt, wie sie eine weitere Möglichkeit zur Klassifizierung von Finanzzeitreihen darstellen könnten.

Epilog

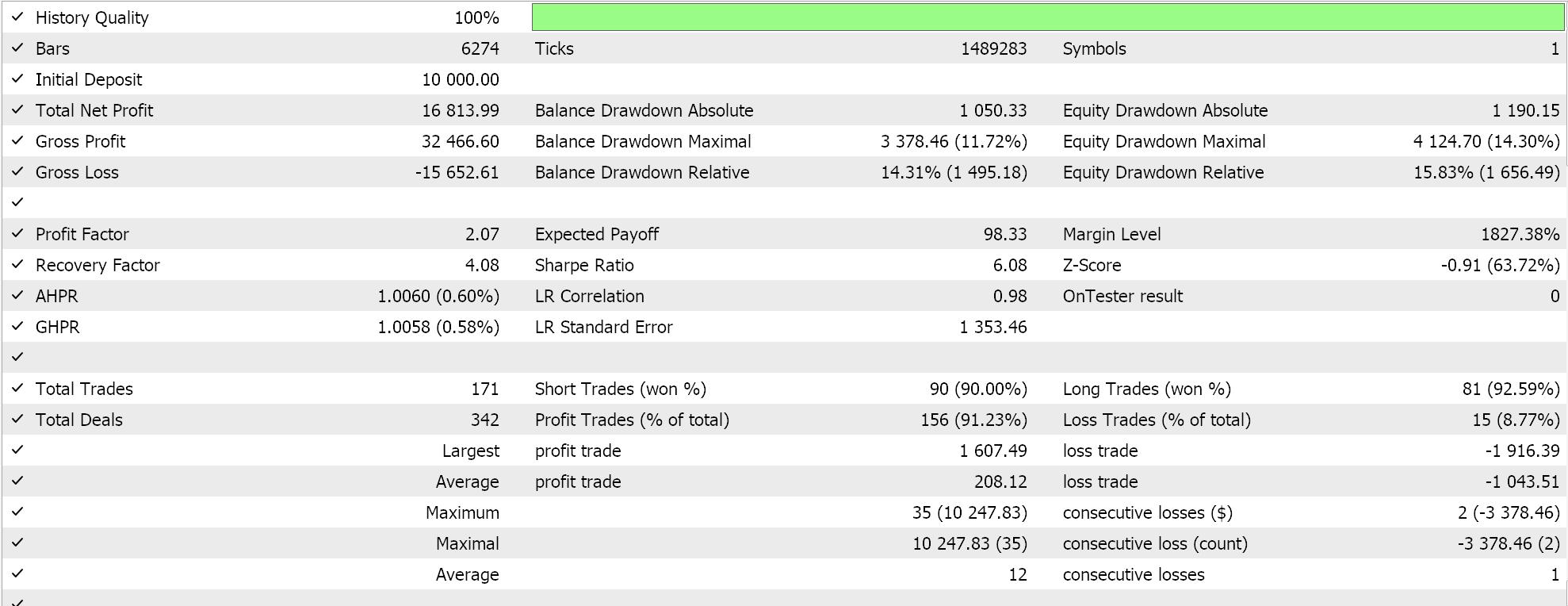
Vergleichende Tests der von den Assistenten zusammengestellten Fachberater sind unten aufgeführt. Beide verwenden das großartige Oszillatorsignal und haben im Prinzip ähnliche Eingänge wie hier angegeben:

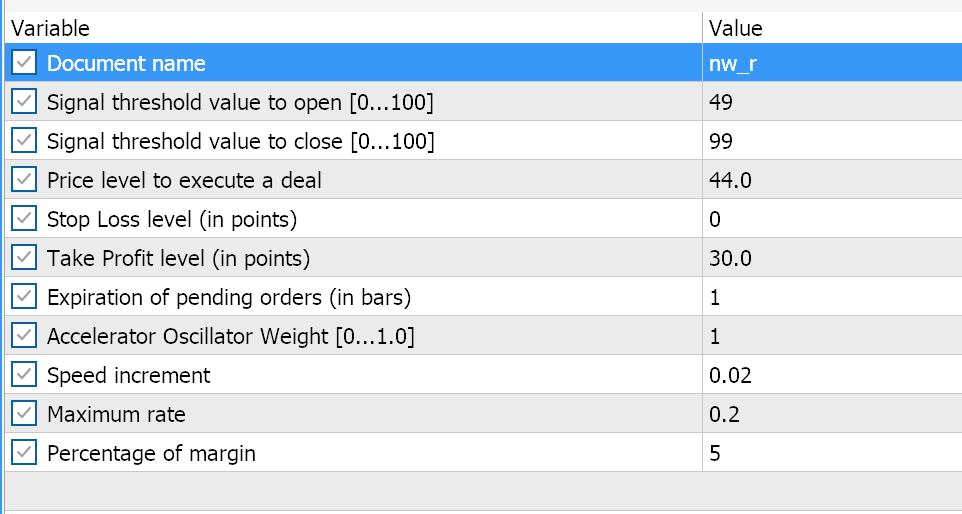
Der Unterschied zwischen ihnen besteht darin, dass der eine Experte den Parabolic Sar zum Nachziehen und Schließen offener Positionen verwendet, während der andere den in diesem Artikel vorgestellten Number-Wall-Algorithmus einsetzt. Allerdings unterscheiden sich ihre Berichte trotz des gleichen Signals, wenn sie auf dem EURUSD im letzten Jahr auf dem stündlichen Zeitrahmen getestet werden. Im Folgenden wird zunächst der parabolische Sar-Trailing-Stop-Experte vorgestellt.

Und der Bericht zur Number Wal ist auch unten angegeben:

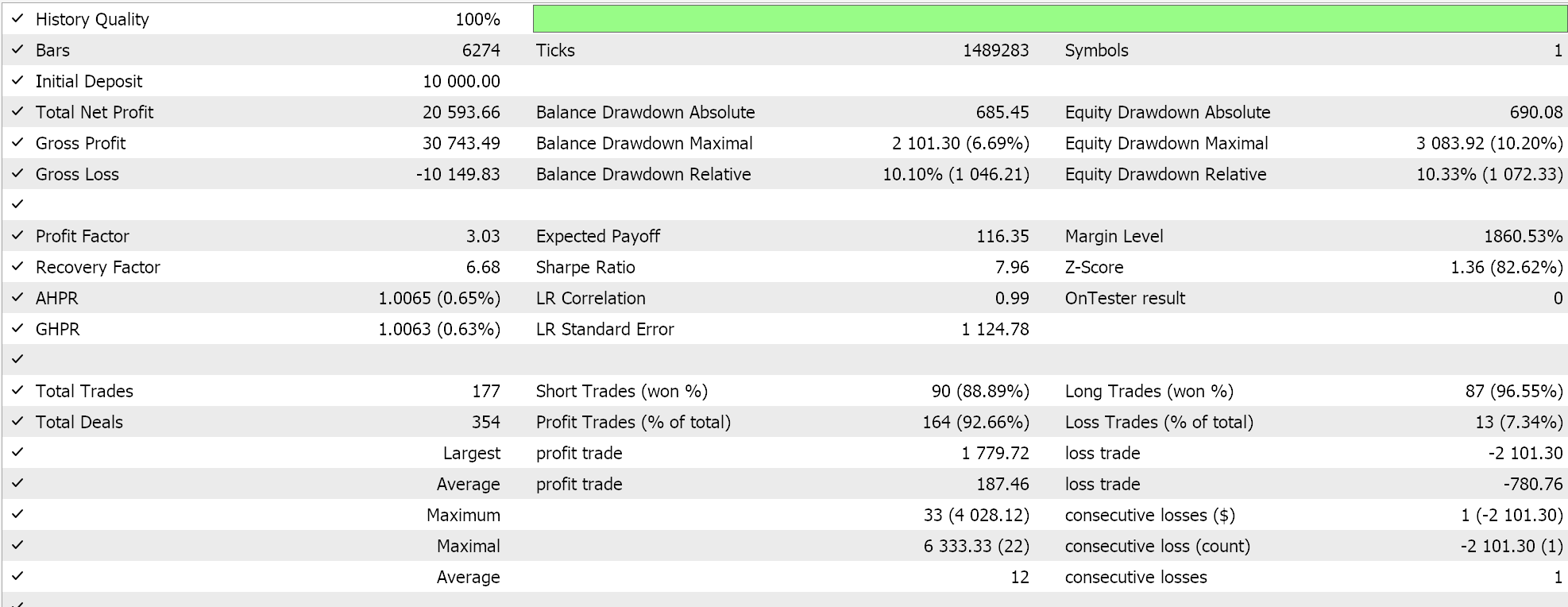
Der Gesamtunterschied im Ergebnis ist nicht signifikant, aber er könnte entscheidend sein, wenn er nicht nur über längere Zeiträume, sondern auch in verschiedenen Expertenklassen wie Geldmanagement oder sogar Signalerzeugung getestet und ausprobiert wird.