A transformação Box-Cox
Victor | 10 março, 2014
Introdução
Enquanto as capacidades do PC aumentarem, negociantes e analistas do Forex têm mais possibilidades de utilização de algoritmos matemáticos complexos e altamente desenvolvidos, que exigem recursos computacionais consideráveis. Mas a adequação dos recursos computacionais não pode resolver os problemas dos negociantes sozinho. Os algoritmos eficientes para análise de cotações do mercado também são necessários.
Atualmente, áreas como estatística matemática, economia e econometria fornecem um grande número de métodos, modelos e algoritmos eficientes em bom funcionamento, ativamente utilizados pelos negociadores para a análise de mercado. Na maioria das vezes estes são métodos paramétricos padrão criados com um pressuposto de estabilidade de sequências pesquisadas e a normalidade da sua lei de distribuição.
Mas não é um segredo que a cotação do Forex são sequências que não podem ser classificadas como sendo estáveis e tendo uma lei de distribuição normal. Portanto, não podemos usar métodos paramétricos "padrão" de estatística matemática, econometria, etc. quando se analisa cotações.
No artigo "Transformação Box-Cox e a ilusão da "normalidade" de séries macroeconômicas [1] A.N. Porunov escreve o seguinte:
"Os analistas econômicos muitas vezes têm de lidar com dados estatísticos que não passam no teste de normalidade por um motivo ou outro. Nesta situação, há duas opções: ou recorrer a métodos não paramétricos, que necessitam de uma quantidade razoável de formação matemática, ou usar técnicas especiais, que permitem converter a "estatística anormal" original em "normal", o que também é uma tarefa bastante complexa".
Apesar do fato de que a cotação de A.N.Porunov refere-se a analistas econômicos, ela pode ser totalmente atribuída a tentativas de analisar as cotações do Forex "anormais", utilizando métodos paramétricos de estatística matemática e econometria. A grande maioria destes métodos tem sido desenvolvido para analisar as sequências que tem a lei de distribuição normal. Mas, na maioria dos casos, o fato da "anormalidade" dos dados inicial é simplesmente ignorada. Além disso, os métodos mencionados muitas vezes exigem não só uma distribuição normal, mas também sequências iniciais de estacionariedade.
Regressão, dispersão (ANOVA) e alguns outros tipos de análise, podem ser chamados de métodos "padrão" que requerem a normalidade de dados inicial. Não é possível listar todos os métodos paramétricos que têm limitações quanto a normalidade da lei de distribuição, uma vez que ocupam toda a área, digamos, da econometria, com exceção de seus métodos não paramétricos.
Para ser justo, deve-se acrescentar que os métodos paramétricos "padrão" têm sensibilidade diferente ao desvio da lei de distribuição de dados inicial do valor normal. Portanto, o desvio da "normalidade" durante o uso de tais métodos não necessariamente leva a consequências desastrosas, mas, é claro, não aumenta a precisão e a confiabilidade dos resultados obtidos.
Tudo que levanta a questão sobre a necessidade de mudar para métodos não paramétricos de análise e previsão das cotações. No entanto, os métodos paramétricos permanecem muito atraentes. Isto pode ser explicado pela sua prevalência e uma quantidade suficiente de dados, algoritmos já prontos e exemplos da sua aplicação. Para usar esses métodos corretamente, é necessário lidar com pelo menos duas questões relacionadas com as sequências iniciais de - instabilidade e "anormalidade".
Embora não possamos influenciar a estabilidade das sequências iniciais, podemos tentar alinhar a sua lei de distribuição para mais próximo da normal. Para resolver este problema, existem várias transformações. As mais conhecidas são descritas resumidamente no artigo "O uso da técnica de transformação Box-Cox na análise estatística e econômica" [2]. Neste artigo, vamos considerar apenas uma delas - a transformação Box-Cox [1], [2], [3].
Devemos salientar aqui que o uso da transformação Box-Cox, tal como qualquer outro tipo de transformação, pode somente executar a lei de distribuição da sequência inicial mais ou menos perto da normal. Isso significa que a utilização desta transformação não garante que a sequência resultante terá a lei de distribuição normal.
1. A transformação Box-Cox
Para a sequência X original do comprimento N
![]()
O único parâmetro de transformação Box-Cox é encontrado como segue:
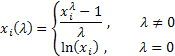
onde ![]() .
.
Como você pode ver, esta transformação tem apenas um parâmetro - lambda. Se o valor de lambda é igual a zero, a transformação logarítmica da sequência inicial é realizada, no caso em que o valor de lambda difere de zero, a transformação é por lei exponencial. Se o parâmetro lambda for igual a um, a lei de distribuição da sequência inicial permanece inalterada, embora a sequência desloque, como unidade, é subtraída de cada um dos seus valores.
Dependendo do valor de lambda, a transformação Box-Cox inclui os seguintes casos especiais:
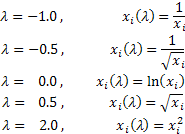
A utilização da transformação Box-Cox exige que todos os valores da sequência de entrada sejam positivos e diferentes de zero. Se a sequência de entrada não atende a esses requisitos, ela pode ser movida para a área positiva, pelo volume que garante a "positividade" de todos os seus valores.
Vamos examinar apenas o parâmetro único de transformação Box-Cox por agora, preparando os dados de entrada para ele de uma forma adequada. A fim de evitar valores negativos ou nulos nos dados de entrada, nós vamos sempre encontrar o menor valor da sequência de entrada e deduzí-lo a partir de cada elemento da sequência, adicionalmente realizando um pequeno deslocamento igual a 1e-5. Tal mudança adicional é necessária para proporcionar um deslocamento de sequência garantido à área positiva, no caso em que seu valor mais baixo é igual a zero.
Na verdade, não é necessário aplicar esse deslocamento nas sequências "positivas". Mas vamos usar o mesmo algoritmo, no entanto, para reduzir a probabilidade de obter valores extremamente grandes ao aumentar a capacidade durante a transformação. Assim, qualquer sequência de entrada estará localizada na área positiva após o deslocamento e terá o menor valor próximo a zero.
Fig. 1, mostra as curvas de transformação Box-Cox, com valores diferentes do parâmetro lambda. Fig. 1, foi tirada do artigo "Transformação Box-Cox" [3]. A grade horizontal no gráfico é dada em uma escala logarítmica.
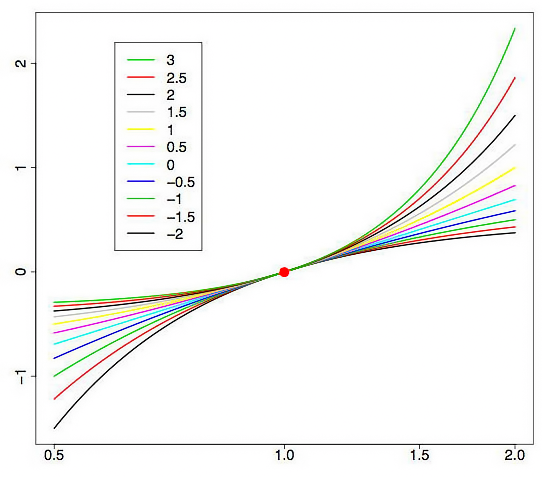
Fig. 1. Transformação Box-Cox no caso de diversos valores do parâmetro lambda
Como podemos ver, as "caudas" da distribuição inicial podem ser "esticadas" ou "apertadas". A curva superior na fig. 1 corresponde com lambda=3, enquanto que a inferior - com lambda=-2.
Para que a lei de distribuição da sequência resultante seja a mais próxima da lei normal quanto possível, o valor ideal do parâmetro lambda deve ser selecionado.
Uma maneira de determinar o valor ideal deste parâmetro é maximizar o logaritmo da função de verossimilhança:
![]()
onde
![]()
Isso significa que precisamos selecionar o parâmetro lambda, em que esta função atinge o seu valor máximo.
O artigo sobre as "transformações Box-Cox" [3] brevemente trata de outra maneira para determinar o valor ideal deste parâmetro com base na procura do mais alto valor do coeficiente de correlação entre os quantis da função de distribuição normal e a sequência transformada classificada. Ao que parece, é possível encontrar alguns outros métodos de otimização do parâmetro lambda, mas primeiro vamos discutir pesquisando o máximo logaritmo da função de verossimilhança mencionado anteriormente.
Existem maneiras diferentes de encontrá-lo. Por exemplo, podemos usar uma simples pesquisa. Para fazer isto, devemos calcular o valor da função de verossimilhança dentro de um intervalo selecionado, mudando o valor do parâmetro lambda em um declive baixo. Além disso, devemos selecionar o parâmetro lambda ideal, em que a função de verossimilhança tem o maior valor.
A distância do declive determinará a precisão do cálculo do valor ideal do parâmetro lambda. Quanto menor for o declive, maior a precisão, embora a quantidade necessária de cálculos é proporcionalmente aumentada neste caso. Vários algoritmos de busca para os algoritmos genéticos de função máxima/mínima e alguns outros métodos podem ser usadospara aumentar a eficiência dos cálculos.
2. Transformação na lei de distribuição normal
Uma das tarefas mais importantes da transformação Box-Cox é a redução da lei de distribuição da sequência de entrada para a forma "normal". Vamos tentar descobrir, o quanto essa questão pode ser bem resolvida com a ajuda desta transformação.
Para evitar qualquer distração e repetições desnecessárias, vamos usar o algoritmo de busca para o mínimo da função pelo método de Powell. Este algoritmo foi descrito nos artigos de "Previsão de séries temporais utilizando aproximação exponencial" e "Previsão de séries temporais utilizando aproximação exponencial" (continuado)".
Devemos criar a classe CBoxCox para procurar o valor ideal do parâmetro de transformação. Nesta classe, a função de verossimilhança acima mencionada, será realizada como objetiva. A classe PowellsMethod [4], [5] é utilizada como básica, realizando diretamente o algoritmo de busca.
//+------------------------------------------------------------------+ //| CBoxCox.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //+------------------------------------------------------------------+ //| CBoxCox class | //+------------------------------------------------------------------+ class CBoxCox:public PowellsMethod { protected: double Dat[]; // Input data double BCDat[]; // Box-Cox data int Dlen; // Data size double Par[1]; // Parameters double LnX; // ln(x) sum public: void CBoxCox(void) { } void CalcPar(double &dat[]); double GetPar(int n) { return(Par[n]); } private: virtual double func(const double &p[]); }; //+------------------------------------------------------------------+ //| CalcPar | //+------------------------------------------------------------------+ void CBoxCox::CalcPar(double &dat[]) { int i; double a; //--- Lambda initial value Par[0]=1.0; Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayResize(BCDat,Dlen); LnX=0; for(i=0;i<Dlen;i++) { //--- input data a=dat[i]; Dat[i]=a; //--- ln(x) sum LnX+=MathLog(a); } //--- Powell optimization Optimize(Par); } //+------------------------------------------------------------------+ //| func | //+------------------------------------------------------------------+ double CBoxCox::func(const double &p[]) { int i; double a,lamb,var,mean,k,ret; lamb=p[0]; var=0; mean=0; k=0; if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;} // Lambda > 5.0 else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0 //--- Lambda != 0.0 if(lamb!=0) { for(i=0;i<Dlen;i++) { //--- Box-Cox transformation BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb; //--- average value calculation mean+=BCDat[i]/Dlen; } } //--- Lambda == 0.0 else { for(i=0;i<Dlen;i++) { //--- Box-Cox transformation BCDat[i]=MathLog(Dat[i]); //--- average value calculation mean+=BCDat[i]/Dlen; } } for(i=0;i<Dlen;i++) { a=BCDat[i]-mean; //--- variance var+=a*a/Dlen; } //--- log-likelihood ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX; return(k+ret); } //------------------------------------------------------------------------------------
Agora, tudo o que temos que fazer para encontrar o valor ideal do parâmetro lambda é referir ao método CalcPar da classe mencionada, fornecendo-lhe a ligação com a matriz que contém os dados de entrada. Podemos adquirir o valor ideal do parâmetro obtido, referindo o método GetPar. Como já foi dito anteriormente, o dado de entrada deve ser positivo.
A classe PowellsMethod implementa o algoritmo de busca para o mínimo da função de muitas variáveis, mas no nosso caso, apenas um único parâmetro é otimizado. Isso lida com o fato de que a dimensão da matriz Par[] é igual a um. Isso significa que a matriz contém apenas um valor. Teoricamente, podemos usar uma variável padrão ao invés da matriz de parâmetros neste caso, mas, isso exigiria a implementação de mudanças dentro do código da classe básica PowellsMethod. Presumivelmente, não haverá qualquer problema se compilarmos o código MQL5 fonte usando as matrizes contendo apenas um elemento.
Devemos levar em consideração o fato de que a função CBoxCox::func() contém uma limitação de alcance dos valores admissíveis dos parâmetros lambda. No nosso caso, este intervalo é limitado a valores de -5 a 5. Isto é feito a fim de evitar a obtenção de valores muito grandes ou muito pequenos ao aumentar os dados de entrada para o grau lambda.
Além disso, se obtermos valores muito grandes ou muito pequenos de lambda durante a otimização, isso pode indicar que a sequência é de pouca utilidade para o tipo de transformação selecionada. Por isso, seria sensato, em qualquer caso, não exceder alguns intervalos razoáveis ao calcular o valor lambda.
3. Sequências aleatórias
Vamos escrever um script teste que realizará a transformação Box-Cox da sequência pseudo-aleatória formada por nós usando a classe CBoxCox.
Abaixo está o código-fonte de um script.
//+------------------------------------------------------------------+ //| BoxCoxTest1.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" #include "RNDXor128.mqh" CBoxCox Bc; RNDXor128 Rnd; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; //--- data size n=1600; //--- input array preparation ArrayResize(dat,n); //--- transformed data array ArrayResize(bcdat,n); Rnd.Reset(); //--- random sequence generation for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp(); //--- input data shift min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; //--- optimization by lambda Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;} else {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);} // Lambda == 0.0 //--- dat[] <-- input data //--- bcdat[] <-- transformed data } //-----------------------------------------------------------------------------------
A sequência pseudo-aleatória com a lei exponencial de distribuição é utilizada como dado de entrada transformado no script mostrado. O comprimento da sequência é definido na variável n e é igual a 1600 valores neste caso.
A classe RNDXor128 (George Marsaglia, Xorshift RNG) é usada para a geração de uma sequência pseudo-aleatória. Essa classe foi descrita no artigo de "Análise das principais características das séries temporais" [6]. Todos os arquivos necessários para a compilação do script BoxCoxTest1.mq5 estão no arquivo Box-Cox-Tranformation_MQL5.zip. Esses arquivos devem estar localizados em um diretório para compilação bem-sucedida.
Quando o script mostrado é executado, a sequência de entrada é formada, movida para a área de valores positivos e a busca do valor ideal do parâmetro lambda é executada. Em seguida, a mensagem contendo o valor de lambda obtido e o número das transmissões de pesquisa do algoritmo são exibidos. A sequência transformada será criada na matriz de informações bcdat[] como resultado.
Este script em sua forma atual permite apenas preparar a sequência transformada para a sua utilização posterior, e não implementa quaisquer alterações. Ao escrever este artigo, o tipo de análise descrito no artigo "Análise das principais características das séries temporais" [6] foi selecionado para a avaliação dos resultados da transformação. Os scripts utilizados para isto, não são mostrados neste artigo para reduzir o volume dos códigos publicados. Apenas os resultados gráficos da análise já feitos são apresentados abaixo.
A Fig. 2 mostra o histograma e o gráfico fornecido pela escala de distribuição normal para a sequência pseudo-aleatória com a lei de distribuição exponencial usada no script BoxCoxTest1.mq5. Resultado do teste de Jarque-Bera JB=3241.73, p=0.000. Como podemos observar, a sequência de entrada não é ao todo "normal" e, como esperado, sua distribuição é semelhante a exponencial.
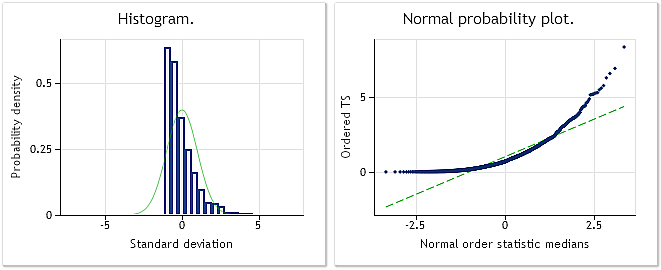
Fig. 2. Sequência pseudo-aleatória com a lei de distribuição exponencial. Teste de Jarque-Bera JB=3241.73, p=0.000.
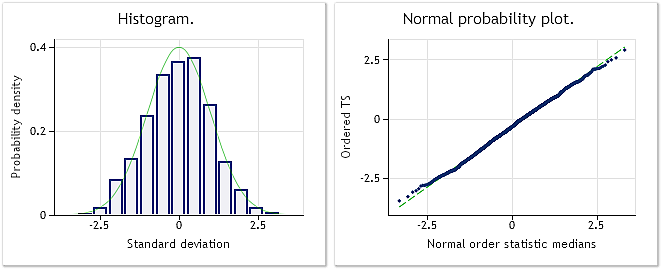
Fig. 3. Sequência transformada. Parâmetro lambda=0.2779, teste de Jarque-Bera JB=4.73, р=0.094
A fig.3 mostra o resultado da análise da sequência transformada (script BoxCoxTest1.mq5, matriz bcdat[]). A lei de distribuição da sequência transformada é muito mais próxima a normal, o que também é confirmado pelos resultados do teste Jarque-Bera JB=4.73, p=0.094. O valor do parâmetro lambda obtido=0,2779.
A transformação Box-Cox provou-se adequada o suficiente neste exemplo. Parece que a sequência resultante tornou-se muito mais próxima a "normal" e o resultado do teste de Jarque-Bera diminuiu de JB=3241.73 para JB=4.73. Isto não é surpresa, uma vez que a sequência escolhida evidentemente se encaixa muito bem nesse tipo de transformação.
Vamos examinar outro exemplo da transformação de Box-Cox da sequência pseudo-aleatória. Devemos criar uma sequência de entrada "adequada" para a transformação Box-Cox, considerando sua natureza de lei exponencial. Para conseguir isso, precisamos gerar uma sequência pseudo-aleatória (que já tem a lei de distribuição próxima a normal) e, em seguida, distorcê-la, aumentando todos os seus valores para a potência de 0.35. Podemos esperar que a transformação Box-Cox retornará a distribuição normal original para a sequência de entrada com grande precisão.
Abaixo está o código-fonte do script do texto BoxCoxTest2.mq5.
Este script difere do anterior apenas pelo fato de que uma outra sequência de entrada é gerada no mesmo.
//+------------------------------------------------------------------+ //| BoxCoxTest2.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" #include "RNDXor128.mqh" CBoxCox Bc; RNDXor128 Rnd; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; //--- data size n=1600; //--- input data array ArrayResize(dat,n); //--- transformed data array ArrayResize(bcdat,n); Rnd.Reset(); //--- random sequence generation for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm(); //--- input data shift min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35); //--- optimization by lambda Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda; } else { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]); } // Lambda == 0.0 //-- dat[] <-- input data //-- bcdat[] <-- transformed data } //-----------------------------------------------------------------------------------
A sequência pseudo-aleatória de entrada com a lei de distribuição normal é gerada no script mostrado. Ela é deslocada para a área de valores positivos e, em seguida, todos os elementos desta sequência são elevados à potência de 0.35. Após a conclusão da operação do script, a matriz dat[] contém a sequência de entrada, enquanto bcdat[] a transformada.
A fig. 4 mostra as características da sequência de entrada que perdeu sua distribuição normal original por causa da elevação à potência de 0.35. Neste caso, o teste de Jarque-Bera mostra JB=3609.29, p= 0.000.
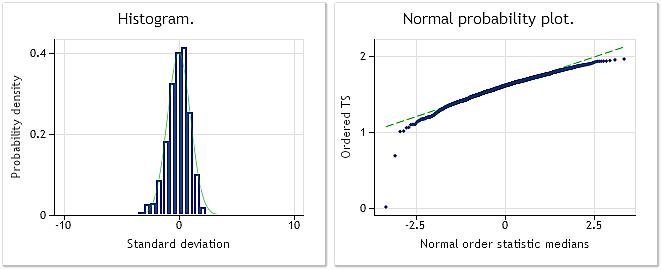
Fig. 4. Sequência pseudo-aleatória de entrada. Teste Jarque-Bera JB=3609.29, p=0.000.
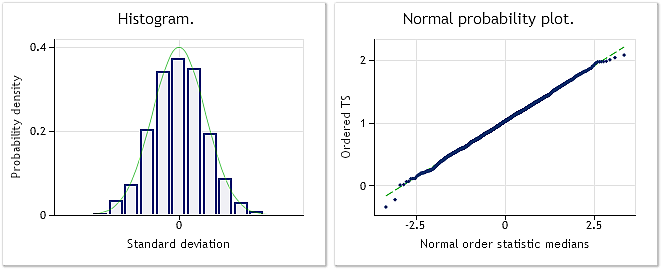
Fig. 5. Sequência transformada. Parâmetro lambda=2.9067, teste de Jarque-Bera JB=0.30, р=0.859
Como mostrado na fig. 5, a sequência transformada tem a lei de distribuição próxima o suficiente da normal, o que também é confirmado pelo valor do teste de Jarque-Bera JB=0.30, p=0.859.
Estes exemplos do uso da transformação Box-Cox têm demonstrado resultados muito bons. Mas, não devemos esquecer, que em ambos os casos temos lidado com as sequências que foram mais convenientes para esta transformação. Portanto, estes resultados podem ser vistos simplesmente como uma confirmação do desempenho do algoritmo que temos criado.
4. Cotações
Depois de ter confirmado o desempenho normal do algoritmo implementando a transformação Box-Cox, devemos tentar aplicá-lo a cotações do Forex reais, conforme queremos reduzi-las à lei de distribuição normal.
Nós vamos usar as sequências que foram descritas no artigo de "Previsão de séries temporais utilizando aproximação exponencial (continuado)" [5] como cotações de teste. Eles são colocados no diretório \ Dataset2 do arquivo Box-Cox-Tranformation_MQL5.zip e fornecem cotações reais de 1200 valores dos quais foram salvos nos arquivos apropriados. A pasta \Dataset2 extraída deve ser colocada no diretório \MQL5\Files do terminal para fornecer acesso a esses arquivos.
Vamos supor que estas cotações não são sequências estacionárias. Portanto, não vamos estender os resultados da análise para a chamada população em geral, mas apenas considerá-los como características desta sequência de comprimento finito particular.
Além disso, deve-se mencionar mais uma vez que, se não houver estacionariedade, os fragmentos de cotações diferentes do mesmo par de moedas seguem amplamente as leis de distribuição diferentes.
Vamos criar um script que permite ler os valores de sequência de um arquivo e executar a sua transformação Box-Cox. A partir dos scripts testes mostrados acima, ele vai diferir apenas no modo de formação da sequência de entrada. Abaixo está o código-fonte de um script, enquanto o script BoxCoxTest3.mq5 está localizado no arquivo anexado.
//+------------------------------------------------------------------+ //| BoxCoxTest3.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" CBoxCox Bc; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; string fname; //--- input data file fname="Dataset2\\EURUSD_M1_1200.txt"; //--- data reading if(readCSV(fname,dat)<0){Print("Error."); return;} //--- data size n=ArraySize(dat); //--- transformed data array ArrayResize(bcdat,n); //--- input data array min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; //--- lambda parameter optimization Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;} else {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);} // Lambda == 0.0 //--- dat[] <-- input data //--- bcdat[] <-- transformed data } //+------------------------------------------------------------------+ //| readCSV | //+------------------------------------------------------------------+ int readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //-----------------------------------------------------------------------------------
Todos os valores (há 1200 deles no nosso caso), são importados para a matriz dat[] nesse script a partir do arquivo de cotações, o nome do qual é definido na variável fname. Mais adiante, a mudança da sequência inicial, buscando pelo valor do parâmetro ideal, e a transformação Box-Cox são realizados na forma como foi descrito acima. Depois que o script foi executado, o resultado da transformação é colocado na matriz bcdat[].
Como pode ser visto a partir do código-fonte mostrado, a sequência das cotações EURUSD M1 foi selecionada no script para a transformação. O resultado da análise da sequência original e transformada é mostrado na fig. 6 e 7.
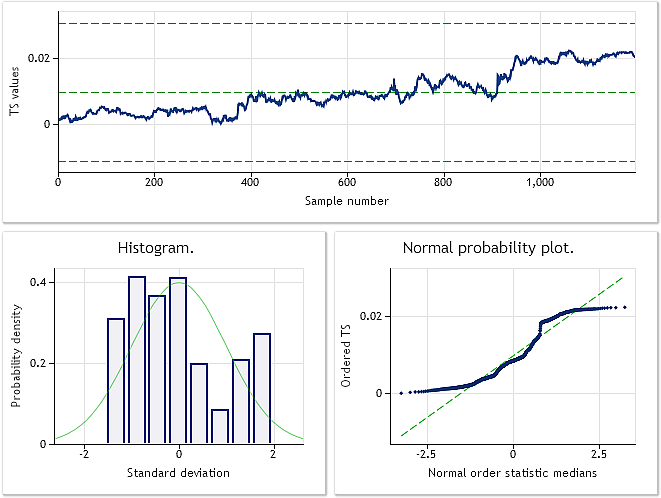
Fig. 6. Sequência de entrada EURUSD M1. Teste Jarque-Bera JB=100.94, p=0.000.
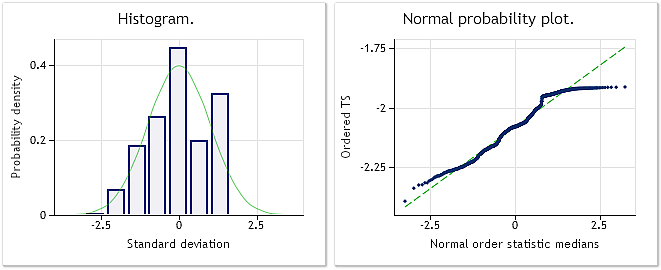
Fig. 7. Sequência transformada. Parâmetro lambda=0.4146, teste de Jarque-Bera JB=39.30, р=0.000
De acordo com as características mostradas na fig. 7, o resultado da transformação da cotação EURUSD M1 não é tão impressionante como os resultados da transformação das sequências pseudo-aleatórias mostradas anteriormente. A transformação de Box-Cox não é capaz de lidar com todos os tipos de sequências de entrada, apesar de ser considerado bastante universal. Por exemplo, é impraticável esperar que a transformação da lei exponencial transforme as duas distribuição do topo em uma normal.
Embora a lei de distribuição representada na fig. 7 dificilmente pode ser considerada normal, ainda podemos ver uma diminuição considerável dos valores de teste Jarque-Bera, como nos exemplos anteriores. Enquanto JB=100.94 para a sequência original, ele mostra JB=39.30 após a transformação. Isso significa que a lei de distribuição conseguiu aproximar os valores normais, em certa medida, após a transformação.
Aproximadamente os mesmos resultados foram obtidos ao transformar fragmentos diferentes de outras cotações. Todas as vezes, a transformação Box-Cox trouxe a lei de distribuição mais para perto da normal, para uma maior ou menor extensão. No entanto, ela nunca se tornou normal.
Uma série de experimentos com várias transformações de cotações permitem tirar a tão esperada conclusão - a transformação Box-Cox permite levar a lei de distribuição de cotações Forex próximo a da normal, mas não pode garantir alcançar a verdadeira normalidade da lei de distribuição de dados transformados.
é sensato realizar a transformação que ainda não trouxe a sequência original para a normal? Não há uma resposta definitiva para esta questão. Em cada caso específico, devemos tomar uma decisão individual sobre a necessidade da transformação Box-Cox. Neste caso, muito vai depender do tipo de métodos paramétricos que são usadosna análise e citações sensibilidade destes métodos para o desvio dos dados iniciais a partir da lei de distribuição normal.
5. Remoção de tendência
A parte superior da fig. 6 mostra o gráfico da sequência original EURUSD M1 usado no script BCTransform.mq5. Pode ser facilmente visto que os seus valores estão aumentando de modo quase uniforme ao longo de toda a sequência. Em uma primeira aproximação, podemos concluir que a sequência contém a tendência linear. A presença de tal "modismo" sugere que devemos tentar excluir a tendência antes de realizar várias transformações e analisar a sequência recebida.
A remoção de uma tendência, das sequências de entrada analisadas,provavelmente não deve ser considerada como um método adequado para absolutamente todos os casos. Mas vamos supor que nós estamos analisando a sequência mostrada na fig. 6 para encontrar os componentes periódicos (ou cíclicos) na mesma. Neste caso, podemos seguramente subtrair a tendência linear a partir da sequência de entrada após a definição dos parâmetros de tendência.
A remoção de uma tendência linear não afetará a detecção de componentes periódicos. Ela ainda pode ser útil e tornar os resultados tal análise mais precisos ou confiáveis, até certo ponto, dependendo do método de análise selecionado.
Se decidirmos que uma remoção de tendência pode ser útil em alguns casos, então provavelmente fará sentido examinar como a transformação Box-Cox lida com uma sequência após uma tendência ter sido excluída da mesma.
Em qualquer situação, ao remover uma tendência teremos que decidir qual curva deve ser usada para a aproximação da tendência? Esta pode ser uma linha reta, curvas de ordem superior, médias móveis, etc. Neste caso, vamos escolher, se assim posso dizer, a versão extrema, a fim de não ser distraído com a questão de seleção da curva ideal. Usaremos os incrementos da sequência original, ou seja, as diferenças entre seus valores atuais e anteriores, em vez da própria sequência original.
Assim que discutimos a análise dos incrementos, é impossível não comentar sobre alguns pontos relacionados.
Em vários artigos e fóruns a necessidade de transição para análise do incremento justifica-se de tal forma que ele pode deixar a impressão errada sobre as propriedades de tal transição. A transição para análise do incremento é muitas vezes descrita como uma espécie de transformação que é capaz de transformar uma sequência original em uma estacionária ou normalizar sua lei de distribuição. Mas é verdade? Vamos tentar responder esta pergunta.
Devemos começar pelo fato de que a essência da transição para análise do incremento é composta de uma ideia muito simples de divisão de uma sequência original em dois componentes. Nós podemos demonstrar isso como segue.
Suponha que temos a sequência de entrada
![]()
E decidimos dividí-la, por qualquer motivo, em uma tendência e alguns elementos restantes que apareceram após a subtração dos valores da tendência a partir dos elementos da sequência original. Suponha que tenhamos decidido usar uma média móvel simples, com um período de nivelamento igual aos dois elementos da sequência para uma aproximação de tendência.
Tal média móvel pode ser calculada como a soma de dois elementos de sequências adjacentes divididos por dois. Neste caso, o resíduo da subtração da média a partir da sequência original será igual a diferença entre os mesmos elementos adjacentes divididos por dois.
Vamos denotar o valor da média mencionado acima como S, enquanto que o resíduo será D. No caso de movermos o fator permanente 2 para a parte esquerda da equação para maior clareza, obteremos como se segue:
![]()
Depois de completar nossas transformações simples de modo correto, dividimos a nossa sequência original em dois componentes, um dos quais é a soma dos valores de sequências adjacentes, e o outro consiste das diferenças. Estas são exatamente as sequências que chamamos de incrementos, enquanto as somas formam a tendência.
Neste aspecto, seria mais razoável considerar os incrementos como uma parte da sequência original. Portanto, não devemos esquecer que, se mudamos para a análise dos incrementos, então a outra parte da sequência definida pelas somas é muitas vezes simplesmente desconsiderada, a menos que não analisemos a mesma separadamente, é claro.
A maneira mais fácil para obter uma idéia de que tipo de benefícios podemos receber com esta divisão da sequência é aplicar o método espectral.
Diretamente a partir das expressões indicadas acima, podemos deduzir que o componente S é o resultado da filtração da sequência original, com a utilização do filtro de baixa frequência, tendo as características de impulso h=1.1. Por conseguinte, o componente D é um resultado da filtração com a utilização do filtro de frequência elevada tendo as características de impulso h=-1.1. A fig. 8 exibe de maneira nominal as características da frequência de tais filtros.
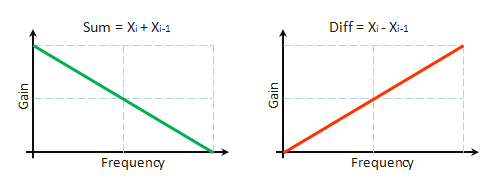
Fig. 8. Características de amplitude da frequência
Suponha que tenhamos mudado da análise direta da própria sequência para a análise de suas diferenças. O que podemos esperar aqui? Existem várias opções nesse caso. Vamos dar uma breve olhada em apenas algumas delas.
- No caso da energia básica do processo analisado estar concentrada na região de baixa frequência da sequência original, a transição à análise das diferenças apenas suprimirá essa energia, tornando-a mais complexa ou mesmo impossível de dar continuidade a análise;
- No caso da energia básica do processo analisado estar concentrada na região de alta frequência da sequência original, a transição à análise das diferenças podem conduzir a efeitos positivos devido a filtração dos componentes de baixa frequência de interferência. Mas isso é possível apenas no caso em que uma filtração não afeta significativamente as propriedades dos processos analisados;
- Também podemos citar o caso em que a energia do processo analisado é distribuída uniformemente por toda a gama de frequência da sequência. Nesse caso, vamos irreversivelmente distorcer o processo após a transição para a análise de suas diferenças, suprimindo a sua parte de baixa frequência.
Da mesma forma, podemos tirar conclusões sobre os resultados da transição à análise de diferenças para quaisquer outras combinações de tendência, tendência de curto prazo, ruído de interferência e assim por diante. Mas em qualquer caso, a transição à análise de diferenças não conduzirá a uma forma estacionária do processo analisado e não normalizará o processo de distribuição.
Com base no dito acima, podemos concluir que a sequência não "melhora" automaticamente após a transição à análise de diferenças. Podemos supor que, em alguns casos, é melhor analisar tanto a sequência de entrada quanto as diferenças, juntamente com a soma dos seus valores adjacentes, para receber um conhecimento mais claro da sequência de entrada, enquanto que devem ser feitas as conclusões finais sobre as propriedades dessa sequência com base na análise conjunta de todos os resultados obtidos.
Vamos voltar ao assunto do nosso artigo e ver como a transformação Box-Cox se comporta no caso da transição à análise dos incrementos da sequência EURUSD M1 mostrada na fig.6. Para fazer isso, usaremos o script BoxCoxTest3.mq5 mostrado anteriormente, nos quais vamos substituir os valores de sequência com as diferenças (incrementos), após calcular esses valores de sequência a partir do arquivo. Visto que não foram implementadas outras alterações ao código-fonte do script, não há nenhum ponto que precise editá-lo. Em vez disso, mostraremos apenas os resultados de sua análise de funcionamento.
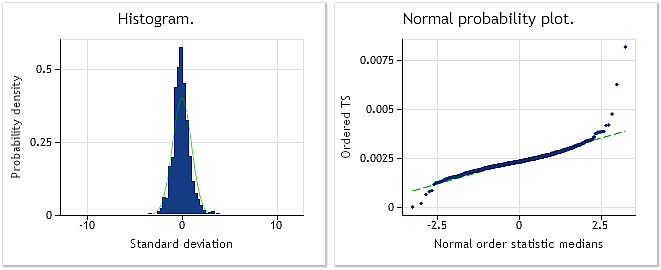
Fig. 9. Incrementos EURUSD M1. Teste Jarque-Bera JB=32494.8, p=0.000.
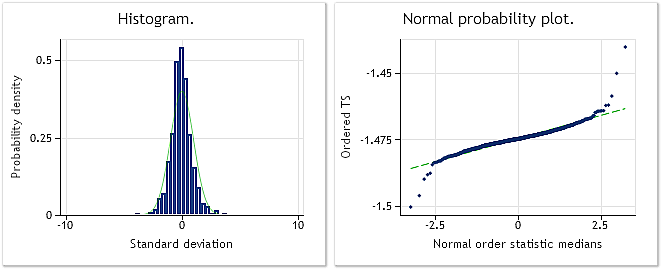
Fig. 10. Sequência transformada. Parâmetro lambda=0.6662, teste de Jarque-Bera JB=10302.5, р=0.000
A fig. 9 mostra as características da sequência que consiste de incrementos (diferenças) EURUSD M1, enquanto que a fig. 10 mostra suas características obtidas após a transformação Box-Cox. Apesar do fato de o valor do teste Jarque-Bera ter diminuído mais de três vezes a partir de JB=32494.8 para JB=10302.5 após a transformação, a lei de distribuição da sequência transformada ainda está longe de ser normal.
No entanto, não devemos saltar para conclusões precipitadas pensando que a transformação Box-Cox não consegue lidar com a transformação dos incrementos corretamente. Nós consideramos apenas um caso especial. Lidando com outras sequências de entrada, podemos obter resultados completamente diferentes.
6. Exemplos citados
Todos os exemplos citados anteriormente da transformação Box-Cox se relacionam com o caso em que a lei de distribuição da sequência original deve ser reduzida para a normal, ou, talvez, para a lei que seja mais próxima do normal quanto possível. Como já foi mencionado no início, tal transformação pode ser necessária quando se utilizam os métodos de análise paramétrica, o que pode ser muito sensível ao desvio de uma lei de distribuição da sequência examinada a partir da normal.
Exemplos apresentados tem demonstrado que em todos os casos após a transformação, de acordo com os resultados do teste Jarque-Bera, temos de fato recebido as sequências que têm a lei de distribuição estando mais perto da normal em comparação as sequências originais. Este fato demonstra claramente a versatilidade e eficiência da transformação Box-Cox.
Mas não devemos superestimar as possibilidades da transformação Box-Cox e supor que qualquer sequência de entrada será transformada estritamente em uma normal. Como pode ser visto a partir dos exemplos acima, isto está longe da verdade. Nem a sequência original ou transformada podem ser consideradas normais para as cotações reais.
A transformação Box-Cox tem sido considerada até o momento apenas na sua forma mais visual de parâmetro único. Isto tem sido feito para simplificar o primeiro contato com ela. Esta abordagem justifica-se a demonstrar as capacidades desta transformação, mas para efeitos práticos, provavelmente seria melhor usar uma forma mais geral de sua apresentação.
7. A forma geral da transformação Box-Cox
Deve ser lembrado que a transformação Box-Cox é aplicável somente às sequências com valores positivos e diferentes de zero. Na prática, esta exigência é facilmente cumprida com um simples deslocamento de uma sequência para a área positiva, mas a magnitude da mudança dentro da área positiva pode ter um impacto direto sobre o resultado da transformação.
Portanto, o valor do deslocamento pode ser considerado como um parâmetro de transformação adicional, otimize-o juntamente com o parâmetro lambda, não permitindo que os valores da sequência entrem na área negativa.
Para a sequência X original do comprimento N:
![]()
as expressões que determinam a forma mais geral dos dois parâmetros de transformação Box-Cox são as seguintes:
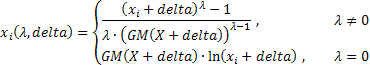
onde:
![]() ;
;
GM() - média geométrica.
A média geométrica da sequência pode ser calculada da seguinte forma:
![]()
Como podemos ver, dois parâmetros já são utilizados nas expressões mostradas - lambda e delta. Agora, temos que otimizar ambos destes parâmetros simultaneamente durante a transformação. Apesar da ligeira complicação do algoritmo, a introdução de um parâmetro adicional pode, certamente, aumentar a eficácia da transformação. Além disso, os fatores de normalização adicionais apareceram nas expressões comparadas com a transformação utilizada anteriormente. Com estes fatores o resultado de transformação vai manter sua dimensão durante a alteração do parâmetro lambda.
Mais informação sobre a transformação Box-Cox pode ser encontrada em [7], [8]. Algumas outras transformações do mesmo tipo são descritas resumidamente em [8].
Aqui estão as principais características da mais presente forma de transformação geral:
- A transformação em si requer que a sequência de entrada contenha apenas valores positivos. A inclusão do parâmetro delta adicional permite realizar automaticamente o deslocamento necessário da sequência ao executar algumas condições definidas;
- Ao selecionar o valor ideal do parâmetro delta, sua magnitude deve garantir "positividade" de todos os valores da sequência;
- A transformação é contínua no caso de alteração do parâmetro lambda incluindo as mudanças próximas do seu valor zero;
- O resultado da transformação mantém sua dimensão no caso de alteração do valor do parâmetro de lambda.
O critério logaritmo da função de verossimilhança foi utilizado em todos os exemplos citados anteriormente ao buscar o valor ideal do parâmetro lambda. Naturalmente, esta não é a única maneira de estimar o valor ideal dos parâmetros de transformação.
Como exemplo, podemos citar o método da otimização de parâmetros, em que o valor máximo do coeficiente de correlação, entre uma sequência transformada classificada de forma ascendente e uma sequência de quantis de função de distribuição normal, é procurado. Esta variante foi anteriormente mencionada no artigo. Os valores dos quantis de função de distribuição normal podem ser calculados de acordo com as expressões sugeridas por James J. Filliben [9].
As expressões que determinam a forma geral da transformação de dois parâmetros são certamente mais difíceis que as anteriormente consideradas. Talvez, esta seja razão do fato pelo qual tal tipo de transformação é muito raramente usado em pacotes matemáticos e estatísticos. As expressões citadas foram realizadas em MQL5 para ter a possibilidade de usar a transformação Box-Cox de uma forma mais geral, se necessário.
O arquivo CFullBoxCox.mqh contém o código-fonte da classe CFullBoxCox que realiza a pesquisa do valor ideal dos parâmetros de transformação. Como já foi mencionado, o processo de otimização é baseado no cálculo do coeficiente de correlação.
//+------------------------------------------------------------------+ //| CFullBoxCox.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //+------------------------------------------------------------------+ //| CFullBoxCox class | //+------------------------------------------------------------------+ class CFullBoxCox:public PowellsMethod { protected: int Dlen; // data size double Dat[]; // input data array double Shift[]; // input data array with the shift double BCDat[]; // transformed data (Box-Cox) double Mean; // transformed data average value double Cdf[]; // Quantile of the distribution cumulative function double Scdf; // Square root of summ of Quantile^2 double R; // correlation coefficient double DeltaMin; // Delta minimum value double DeltaMax; // Delta maximum value double Par[2]; // parameters array public: void CFullBoxCox(void) { } void CalcPar(double &dat[]); double GetPar(int n) { return(Par[n]); } private: double ndtri(double y0); // the function opposite to the normal distribution function virtual double func(const double &p[]); }; //+------------------------------------------------------------------+ //| CalcPar | //+------------------------------------------------------------------+ void CFullBoxCox::CalcPar(double &dat[]) { int i; double a,max,min; Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayResize(Shift,Dlen); ArrayResize(BCDat,Dlen); ArrayResize(Cdf,Dlen); //--- copy the input data array ArrayCopy(Dat,dat); Scdf=0; a=MathPow(0.5,1.0/Dlen); Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1]; Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0]; a=Dlen+0.365; for(i=1;i<(Dlen-1);i++) { //--- calculation of the distribution cumulative function Quantile Cdf[i]=ndtri((i+0.6825)/a); //--- calculation of the sum of Quantile^2 Scdf+=Cdf[i]*Cdf[i]; } //--- square root of the sum of Quantile^2 Scdf=MathSqrt(Scdf); min=dat[0]; max=min; for(i=0;i<Dlen;i++) { //--- copy the input data a=dat[i]; Dat[i]=a; if(min>a)min=a; if(max<a)max=a; } //--- Delta minimum value DeltaMin=1e-5-min; //--- Delta maximum value DeltaMax=(max-min)*200-min; //--- Lambda initial value Par[0]=1.0; //--- Delta initial value Par[1]=(max-min)/2-min; //--- optimization using Powell method Optimize(Par); } //+------------------------------------------------------------------+ //| func | //+------------------------------------------------------------------+ double CFullBoxCox::func(const double &p[]) { int i; double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret; lam=p[0]; del=p[1]; k1=0; k2=0; if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;} // Lambda > 5.0 else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;} // Lambda < -5.0 if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;} // Delta > DeltaMax else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin gm=0; for(i=0;i<Dlen;i++) { Shift[i]=Dat[i]+del; gm+=MathLog(Shift[i]); } //--- geometric mean gm=MathExp(gm/Dlen); gmpow=lam*MathPow(gm,lam-1); mean=0; //--- Lambda != 0.0 if(lam!=0) { for(i=0;i<Dlen;i++) { a=(MathPow(Shift[i],lam)-1.0)/gmpow; //--- transformed data (Box-Cox) BCDat[i]=a; //--- average value mean+=a; } } //--- Lambda == 0.0 else { for(i=0;i<Dlen;i++) { a=gm*MathLog(Shift[i]); //--- transformed data (Box-Cox) BCDat[i]=a; //--- average value mean+=a; } } mean=mean/Dlen; //--- sorting of the transformed data array ArraySort(BCDat); a=0; b=0; for(i=0;i<Dlen;i++) { c=(BCDat[i]-mean); a+=Cdf[i]*c; b+=c*c; } //--- correlation coefficient ret=a/(Scdf*MathSqrt(b)); return(k1+k2-ret); } //+------------------------------------------------------------------+ //| The function opposite to the normal distribution function | //| Prototype: | //| Cephes Math Library Release 2.8: June, 2000 | //| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier | //+------------------------------------------------------------------+ double CFullBoxCox::ndtri(double y0) { static double s2pi =2.50662827463100050242E0; // sqrt(2pi) static double P0[5]={-5.99633501014107895267E1, 9.80010754185999661536E1, -5.66762857469070293439E1, 1.39312609387279679503E1, -1.23916583867381258016E0}; static double Q0[8]={ 1.95448858338141759834E0, 4.67627912898881538453E0, 8.63602421390890590575E1, -2.25462687854119370527E2, 2.00260212380060660359E2, -8.20372256168333339912E1, 1.59056225126211695515E1, -1.18331621121330003142E0}; static double P1[9]={ 4.05544892305962419923E0, 3.15251094599893866154E1, 5.71628192246421288162E1, 4.40805073893200834700E1, 1.46849561928858024014E1, 2.18663306850790267539E0, -1.40256079171354495875E-1,-3.50424626827848203418E-2, -8.57456785154685413611E-4}; static double Q1[8]={ 1.57799883256466749731E1, 4.53907635128879210584E1, 4.13172038254672030440E1, 1.50425385692907503408E1, 2.50464946208309415979E0, -1.42182922854787788574E-1, -3.80806407691578277194E-2,-9.33259480895457427372E-4}; static double P2[9]={ 3.23774891776946035970E0, 6.91522889068984211695E0, 3.93881025292474443415E0, 1.33303460815807542389E0, 2.01485389549179081538E-1, 1.23716634817820021358E-2, 3.01581553508235416007E-4, 2.65806974686737550832E-6, 6.23974539184983293730E-9}; static double Q2[8]={ 6.02427039364742014255E0, 3.67983563856160859403E0, 1.37702099489081330271E0, 2.16236993594496635890E-1, 1.34204006088543189037E-2, 3.28014464682127739104E-4, 2.89247864745380683936E-6, 6.79019408009981274425E-9}; double x,y,z,y2,x0,x1,a,b; int i,code; if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);} if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);} code=1; y=y0; if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;} // 0.135... = exp(-2) if(y>0.13533528323661269189) // 0.135... = exp(-2) { y=y-0.5; y2=y*y; a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i]; b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i]; x=y+y*(y2*a/b); x=x*s2pi; return(x); } x=MathSqrt(-2.0*MathLog(y)); x0=x-MathLog(x)/x; z=1.0/x; //--- y > exp(-32) = 1.2664165549e-14 if(x<8.0) { a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i]; b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i]; x1=z*a/b; } else { a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i]; b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i]; x1=z*a/b; } x=x0-x1; if(code!=0)x=-x; return(x); } //------------------------------------------------------------------------------------
Algumas limitações são aplicadas às faixas de alteração dos parâmetros de transformação durante a otimização. O valor do parâmetro lambda está limitado por valores 5.0 e -5.0. As limitações dos parâmetros delta são especificadas em relação ao valor mínimo da sequência de entrada. Este parâmetro é limitado por valores de DeltaMin=(0.00001-min) e DeltaMAX=(max-min)*200-min, onde min e max são os valores mínimo e máximo dos elementos da sequência de entrada.
O script FullBoxCoxTest.mq5 demonstra o uso da classe CFullBoxCox. O código fonte desse script é mostrado abaixo.
//+------------------------------------------------------------------+ //| FullBoxCoxTest.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CFullBoxCox.mqh" CFullBoxCox Bc; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],shift[],bcdat[],lambda,delta,gm,gmpow; string fname; //--- input file name fname="Dataset2\\EURUSD_M1_1200.txt"; //--- reading the data if(readCSV(fname,dat)<0){Print("Error."); return;} //--- data size n=ArraySize(dat); //--- shifted input data array ArrayResize(shift,n); //--- transformed data array ArrayResize(bcdat,n); //--- lambda and delta parameters optimization Bc.CalcPar(dat); lambda=Bc.GetPar(0); delta=Bc.GetPar(1); PrintFormat("Iterations= %i, lambda= %.4f, delta= %.4f", Bc.GetIter(),lambda,delta); gm=0; for(i=0;i<n;i++) { shift[i]=dat[i]+delta; gm+=MathLog(shift[i]); } //--- geometric mean gm=MathExp(gm/n); gmpow=lambda*MathPow(gm,lambda-1); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;} else {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);} //--- dat[] <-- input data //--- shift[] <-- input data with the shift //--- bcdat[] <-- transformed data } //+------------------------------------------------------------------+ //| readCSV | //+------------------------------------------------------------------+ int readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //------------------------------------------------------------------------------------
A sequência de entrada é enviada para a matriz dat[] do arquivo no começo do script e, em seguida, a busca dos valores ideias dos parâmetros de transformação é realizada. Então, a transformação em si é realizada com a utilização dos parâmetros obtidos. Como resultado, a matriz dat[] contém a sequência original, a matriz shift[] contém a sequência original deslocada pelo valor delta e a matriz bcdat[] contém o resultado da transformação Box-Cox.
Todos os arquivos necessários para a compilação do script FullBoxCoxTest.mq5 estão localizados no arquivo Box-Cox-Tranformation_MQL5.zip.
A transformação das sequências de teste que usamos é realizada com a ajuda do script FullBoxCoxTest.mq5. Como foi esperado, durante a análise dos dados obtidos podemos concluir que este tipo de transformação de dois parâmetros mostra de certa forma melhores resultados comparando com o tipo de um parâmetro. Por exemplo, para a sequência de EURUSD M1, os resultados da análise dos quais são mostrados na fig. 6, o valor do teste Jarque-Bera compreendeu JB=100.94. JB=39.30 após a transformação de um parâmetro (ver fig. 7), mas após a transformação de dois parâmetros (script FullBoxCoxTest.mq5), este foi para JB=37.49.
Conclusão
Neste artigo examinamos os casos em que os parâmetros de transformação Box-Cox foram otimizados para que a lei de distribuição da sequência resultante fosse a mais próxima da normal possível. Mas, na prática, os casos podem ocorrer quando a transformação Box-Cox deve ser utilizada de uma maneira ligeiramente diferente. Por exemplo, o seguinte algoritmo pode ser usado ao prever as sequências de tempo:
- Os valores preliminares dos modelos de previsão e valores dos parâmetros de transformação Box-Cox são selecionados;
- A transformação Box-Cox dos dados de entrada é realizada;
- A previsão é realizada de acordo com os parâmetros atuais;
- A transformação Box-Cox reversa é realizada para os resultados de previsão;
- O erro de previsão é avaliado pela sequência de entrada não transformada;
- Os valores dos parâmetros são alterados para minimizar o erro de previsão e o retorno do algoritmo ao passo 2.
No algoritmo acima, os parâmetros de transformação devem ser minimizados, bem como os modelo de previsão, através do critério mínimo de erro de previsão. Neste caso, o objetivo da transformação Box-Cox já não é a transformação da sequência de entrada na lei de distribuição normal.
Agora, é necessário transformar a sequência de entrada para receber a lei de distribuição fornecendo o mínimo de erro de previsão. Dependendo do método de previsão selecionado, esta lei de distribuição não têm necessariamente que ser normal.
A transformação Box-Cox é aplicável apenas a sequências com valores positivos e diferentes de zero. A mudança da sequência de entrada deve ser realizada em todos os outros casos. Esta característica da transformação pode certamente ser chamada de um dos seus inconvenientes. Mas, apesar disso, a transformação Box-Cox é provavelmente a ferramenta mais versátil e eficiente, entre outras transformações do mesmo tipo.
Lista de referências
- А.N. Porunov. Box-Сox Transformation and the Illusion of «Normality» of Macroeconomic Series. "Business Informatics" journal, №2(12)-2010, pp. 3-10.
- Mohammad Zakir Hossain, The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses. Journal of Emerging Trends in Economics and Management Sciences (JETEMS) 2(1):32-39.
- Box-Cox Transformations.
- The article "Time Series Forecasting Using Exponential Smoothing".
- The article "Time Series Forecasting Using Exponential Smoothing (continued)".
- Analysis of the Main Characteristics of Time Series.
- Power transform.
- Draper N.R. and H. Smith, Applied Regression Analysis, 3rd ed., 1998, John Wiley & Sons, New York.
- Q-Q plot.