Cálculo do coeficiente de Hurst
Dmitriy Piskarev | 22 março, 2017
Introdução
A definição da dinâmica do mercado é uma das principais tarefas do trader. Geralmente é muito difícil tomar conta disto com a ajuda das ferramentas padrão da análise técnica. Por exemplo, a MA ou a MACD podem indicar a presença de uma tendência, porém, sem ferramentas adicionais nós não podemos avaliar se estamos perante uma tendência forte, estável e verdadeira, e é bastante possível que se trate de um pico de curto prazo que desaparecerá rapidamente.
Lembremo-nos do axioma: para negociar com sucesso no mercado Forex, é sempre importante saber um pouco mais do que os outros traders. Neste caso, você estará um passo à frente, poderá escolher os mais vantajosos pontos de entrada e ter a certeza da rentabilidade da negociação. Uma negociação bem-sucedida tem a ver com uma combinação de vários recursos: a colocação de ordens de compra e venda no momento exato da quebra da tendência, a adequada análise em dados fundamentais e técnicos, e, claro, uma completa falta de emoções e sentimentos. Tudo isto é a chave para uma carreira bem-sucedida.
A análise fractal pode ser uma solução abrangente para muitos problemas no campo das avaliações de mercado. Traders e investidores descuidam injustamente esta ferramenta, no entanto a análise fractal de séries temporais ajuda a avaliar efetivamente a presença e a estabilidade da tendência no mercado. O coeficiente de Hurst é uma das unidades básicas da análise fractal.
Antes de passar diretamente para os cálculos, consideremos brevemente as disposições fundamentais da análise fractal e conheçamos melhor o coeficiente de Hurst.
1. Teoria do mercado fractal (FMT). Análise fractal
Um fractal é um conjunto matemático que tem a propriedade de auto-similaridade. Em outras palavras, trata-se de um objeto que coincide exata ou aproximadamente com uma parte de si mesmo, ou seja, sua totalidade tem a mesma forma de uma ou mais partes. O exemplo mais revelador da estrutura fractal é a "árvore fractal":

Ao conceito de auto-similaridade pode ser dada uma definição melhor, isto é: um objeto com auto-similaridade é estatisticamente semelhante em diferentes escalas quer espaciais quer temporais.
Num contexto de mercado, a palavra "fractal" significa "que se repete" ou "cíclico".
A dimensão fractal é uma caraterística que define como um objeto ou um processo preenche o espaço. Ela descreve como se altera a estrutura do objeto ao ser redimensionado. Ao projetar esta definição nos mercados financeiros (neste caso, de moedas), pode ser postulado que a dimensão fractal determina o grau de "irregularidade" ou variabilidade das séries temporais. Por conseguinte, a linha reta tem uma dimensão d igual a um, o passeio aleatório é d=1.5, enquanto para a série temporal fractal temos 1<d<1.5 ou 1.5<d<1.
"O propósito da hipótese do mercado fractal é fornecer um modelo de comportamento do investidor e dos movimentos do preço de mercado que correspondem às nossas observações... Num determinado momento, os preços podem não refletir todas as informações disponíveis, eles podem refletir apenas a informação que é importante para um horizonte de investimento específico - "Análise fractal dos mercados financeiros", E. Peters.
Neste artigo não vamos discutir em detalhe o conceito de fractal, uma vez que contamos com o fato de o leitor ter uma ideia deste método de análise. Uma descrição exaustiva da sua aplicação nos mercados financeiros pode ser encontrada nos trabalhos de Benoit Mandelbrot e Richard L. Hudson (the Misbehavior of Markets: A Fractal View of Financial Turbulence); Edgar E. Peters "Fractal Market Analysis: Applying Chaos Theory to Investment and Economics", "Chaos and Order in the Capital Markets. A New View of Cycles, Prices, and Market Volatility".
2. Análise R/S e coeficiente de Hurst
2.1. Surgimento da análise R/S
O parâmetro chave da análise fractal é o exponente de Hurst. Esta medida é utilizada na análise de séries temporais. Quanto maior o atraso entre os dois pares idênticos de valores na série temporal, menor é o coeficiente de Hurst.
Este importante indicador foi introduzido por Harold Edwin Hurst, hidrólogo britânico que fez parte do projeto de barragem no rio Nilo, no Egito. Para a construção, era necessário estimar o fluxo de água e a necessidade de escoamento. Inicialmente, acreditava-se que o fluxo de água era uma variável aleatória, processo estocástico. No entanto, Hurst estudou os registros sobre as inundações do Nilo durante nove séculos e encontrou um padrão. Este foi o ponto de partida do estudo. Verificou-se que as enchentes maiores do que a média eram substituídas por enchentes maiores. Depois disso, o processo alterou sua direção, e as enchentes num nível abaixo da média foram substituídas por outras ainda menores. Havia ciclos com uma duração não periódica.
A base do modelo estatístico de Hurst foi o trabalho de Albert Einstein sobre o movimento browniano, que, por sua vez, é essencialmente o modelo de passeio aleatório de partículas. A essência da teoria consiste em que a distância percorrida pela partícula, R, aumenta proporcionalmente à raiz quadrada do tempo T:
![]()
Parafraseando a fórmula; a magnitude da variação, R, ao fazer muitos testes é igual à raiz quadrada a partir do número de testes, T. Esta fórmula foi tomada por Hurst como base para provar que as inundações do Nilo não eram por acaso.
Para a formação de seu método, o hidrólogo usou a séries temporal X1..Xn valores da enchida. Em seguida implementou o seguinte algoritmo, chamado mais tarde de método de escala normalizada ou análise R/S:
- Cálculo do valor médio, Xm, série X1..Xn
- Cálculo do desvio padrão, S
- Normalização da série subtraindo a partir da cada valor de média, Zr, onde r=1..n
- Criação de uma série temporal cumulativa Y1=Z1+Zr, onde r=2..n
- Cálculo da magnitude da série temporal cumulativa R=max(Y1..Yn)-min(Y1..Yn)
- Divisão da magnitude da série temporal cumulativa pelo desvio padrão S.
Hurst expandiu a equação de Einstein e levou-a para uma forma mais geral:
![]()
onde c é a constante.
Em geral, o sistema R/S altera a escala com incrementos crescentes de tempo de acordo com o valor de um grau de dependência igual a H que normalmente é chamado de expoente de Hurst.
O hidrólogo tomava o indicador H como 0,5 quando o processo de enchente era acidental. Descobriu-se que, após o estudo e cálculo, quando o processo enchimento era acidental o expoente H em vez de ser igual a 0,5 era 0,91! Assim a magnitude normalizada muda mais rapidamente do que a raiz quadrada do tempo, ou seja, o sistema passa uma distância maior do que o processo probabilístico. Este fato é a premissa do momento em que se pode afirmar que os acontecimentos do passado têm um impacto significativo sobre o presente e o futuro.
2.2. Aplicação da teoria aos mercados
Após isto, foi desenvolvida uma técnica de cálculo do coeficiente de Hurst aplicada aos mercados financeiros e bolsistas. Esse recurso inclui a normalização de dados para a média zero e o desvio padrão unitário para compensar o componente de inflação. Em outras palavras, temos novamente de lidar com a análise R/S.
Como é interpretado o coeficiente de Hurst nos mercados?1. Se o expoente Hurst estiver na faixa 0,5-1 e diferir do valor esperado em mais de dois desvios padrão, o processo será caracterizado pela memória de longo prazo. Em outras palavras, existe uma persistência.
Isto significa que, dentro de um certo período, os seguintes parâmetros dependem fortemente dos anteriores. Como exemplos ilustrativos de série temporal persistente temos os gráficos de cotações das empresas mais duradouras e influentes. Por exemplo, a Apple, GE, Boeng, Rosneft, Aeroflot e VTB. Abaixo está um gráfico de cotações destas empresas. Eu acho que cada investidor praticante reconheceu nestas imagens o familiar situação "cada novo pico e fundo maiores do que os anteriores."
Cotações de ações da Aeroflot:
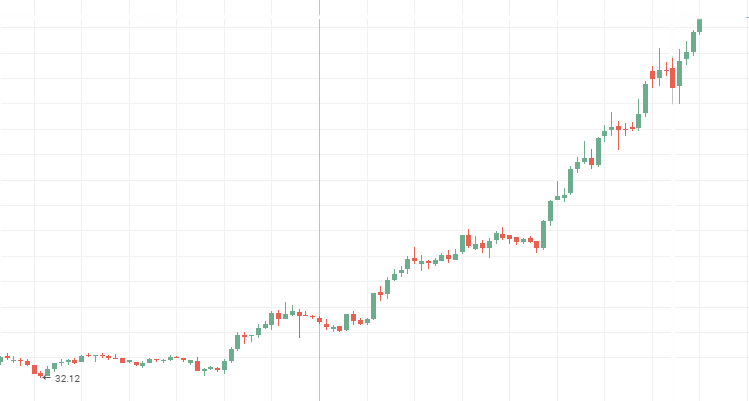
Cotações de ações da Rosneft:
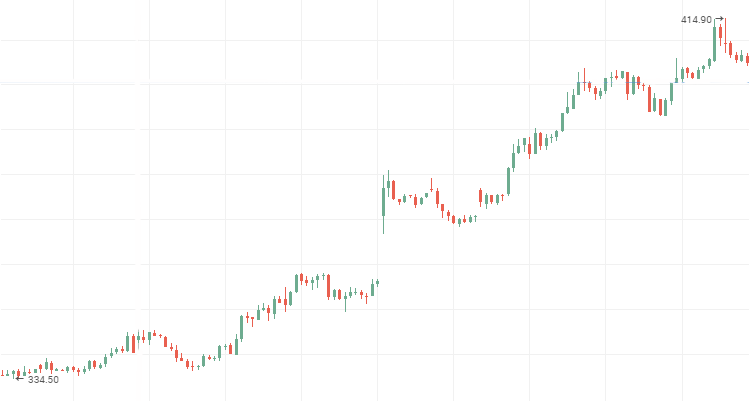
Cotações de ações VTB, série temporal persistente descendente
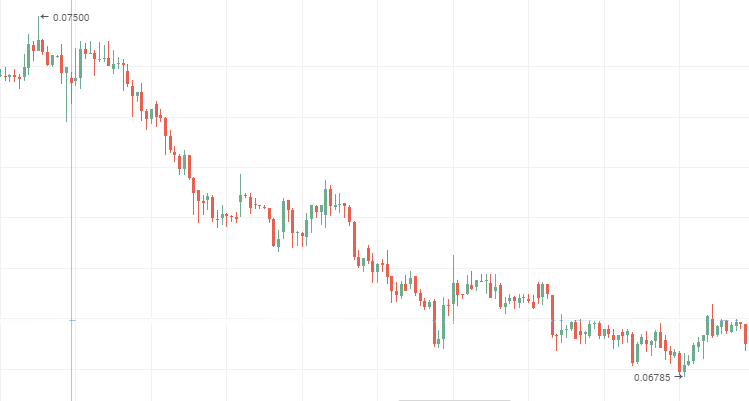
2. O expoente de Hurst, que difere do valor esperado em valor absoluto em dois ou mais desvios-padrão e que leva o valor do intervalo de 0 a 0,5, caracteriza a série temporal antipersistente.
O sistema muda mais rápido do que o aleatório, ou seja, tem frequentes mudanças, mas pequenas. Os gráficos de cotações de ações do segundo escalão são um processo antipersistente. Durante o período de estagnação do preço, tais gráficos mostram as "blue chips". Abaixo estão as tabelas de preços para as ações da Mechel, AvtoVAZ, Lenenergo, elas são claros exemplos de séries temporais antipersistentes.
Ações preferenciais da companhia "Mechel":
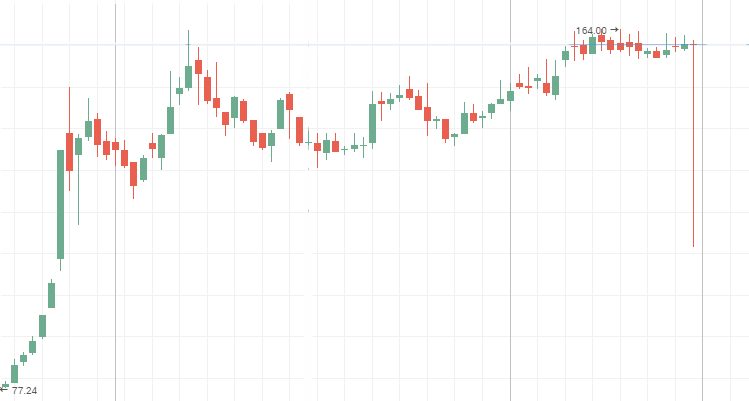
Movimento lateral das ações comuns da AvtoVAZ:
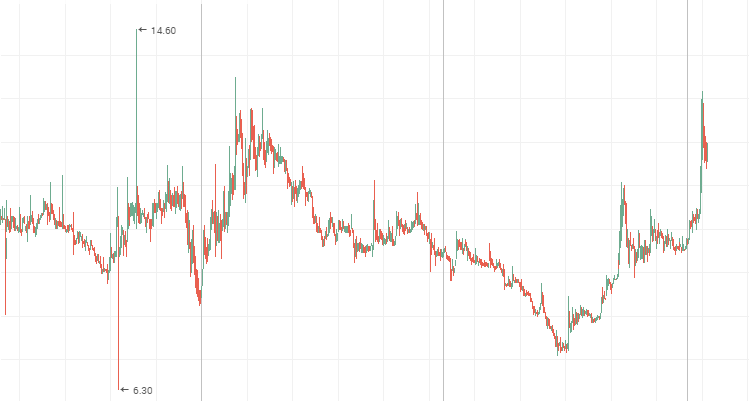
"Lenenergo":
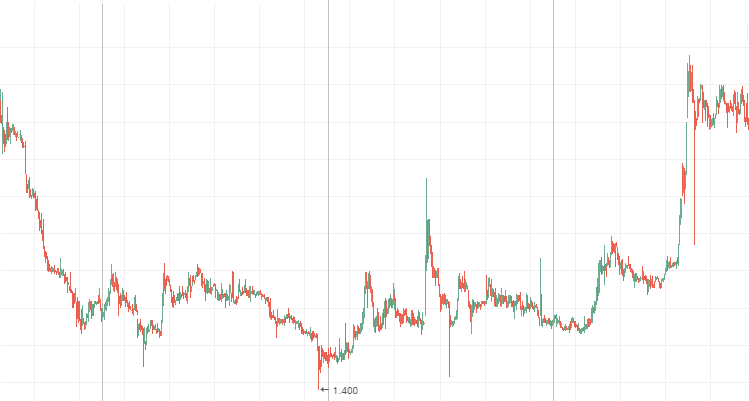
3. Se o expoente de Hurst é igual a 0.5 ou seu valor difere do valor esperado em menos do que dois desvios-padrão, por um lado, o processo é considerado como um passeio aleatório, e, por outro lado, a probabilidade de uma dependência cíclica de longo ou curto prazo é considerada mínima. Na verdade, isso significa que, durante a negociação, não vale a pena se confiar na análise técnica, uma vez que os valores do passado têm pouco efeito sobre o presente. Aqui, a melhor solução é usar a análise fundamental.
Na tabela abaixo, há exemplos dos valores do exponente de Hurst para os instrumentos do mercado de ações, isto é, títulos de várias corporações, empresas industriais, mercadorias. O cálculo foi realizado durante os últimos 7 anos. Observe que os baixos valores do coeficiente, nas "blue chips", mostra que há muitas empresas em fase de consolidação durante a crise financeira. Curiosamente, muitas ações a parti do Índice de ações do segundo nível exibem um processo persistente, o que fala sobre sua resistência à crise.
| Nome | Expoente de Hurst, H |
|---|---|
| Gazprom |
0.552 |
| VTB |
0.577 |
| Magnético |
0.554 |
| MTS |
0.543 |
| Rosneft |
0.648 |
| Aeroflot | 0.624 |
| Apple | 0.525 |
| GE | 0.533 |
| Boeing | 0.548 |
| Rosseti |
0.650 |
| Raspadskaya |
0.656 |
| TGC-1 |
0.641 |
| Tattelecom |
0.582 |
| Linergo |
0.642 |
| Mechel |
0.635 |
| AvtoVAZ |
0.574 |
| Gasolina | 0.586 |
| Estanho | 0.565 |
| Paládio | 0.564 |
| Gás natural | 0.560 |
| Níquel | 0.580 |
3. Determinação de ciclos e memória na análise fractal
Surge a pergunta: por que precisamos ter certeza de que nossos resultados não são aleatórios (triviais)? Para dar resposta, primeiro, examinamos os resultados da análise RS, assumindo que o sistema a ser estudado é aleatório. Ou seja, verificamos a validade da hipótese nula, isto é, se o processo é um passeio aleatório e sua estrutura independente e normalmente distribuída.
3.1. Calculo do valor esperado da análise R/S
Introduzimos o conceito de valor esperado de análise R/S.
Anis e Lloyd em 1976 derivaram uma equação que expressava o valor esperado que nós precisamos:
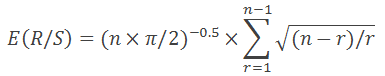
Onde n é o número de observações e r, os inteiros de um a n-1.
Como se observa no livro "Análise fractal dos mercados financeiros", a fórmula acima é válida somente para n>20. Para n<20, deve ser utilizada a seguinte fórmula:
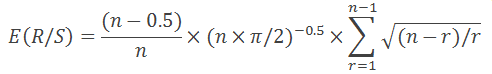
Tudo é muito simples:
- Para cada número de observações, calculamos o valor esperado e traçamos o gráfico resultante Log(E(R/S)) a partir de Log(N) juntamente com Log(R/S) a partir de Log(N);
- calculamos a dispersão esperada do exponente de Hurst de acordo com a conhecida fórmula a partir da teoria estatística
![]()
onde H é o exponente de Hurst;
N é o número de observações na amostragem;
3. verificamos o valor do coeficiente de Hurst obtido através da estimativa do número de desvios padrão nos quais H ultrapassa E(H). É considerado como significativo o resultado onde o exponente de importância é superior a 2.
3.2. Definição de ciclos
Para não sermos infundados, examinemos o exemplo. Construímos dois gráficos, um para estatísticas RS e outro para o valor esperado E(R/S), logo, comparamos com a dinâmica do mercado. Será que os resultados dos cálculos concordam com a dinâmica das cotações?
Recordemos que Peters apontava que a melhor maneira de entender o ciclo era construir um gráfico de estatística V numa escala logarítmica a partir do logaritmo do número de observações no subgrupo.
Avaliar o resultado da construção é muito simples:
- se o gráfico, numa escala logarítmica, em ambos os eixos é uma linha horizontal, então estamos lidando com um processo aleatório independente;
- se o gráfico tem um ângulo positivo ascendente, estamos lidando com um processo persistente, segundo o qual, novamente, as alterações na escala R/S acontecem mais rápido do que a raiz quadrada do tempo;
- e, finalmente, se o gráfico mostra uma tendência de queda, o presente processo é antipersistente.
3.3. Memória na análise fractal e determinação de sua profundidade
Para entender melhor a essência da análise fractal, introduzimos o conceito de memória.
Já foram mencionadas construções verbais como as memórias de curto prazo e de longo prazo. Na análise fractal, a memória refere-se a um período durante o qual o mercado se lembra do passado e leva em conta seu impacto sobre os acontecimentos atuais e futuros. Este período é chamado de profundidade de memória. Neste conceito, até certo ponto, está toda a força e especificidade da análise fractal. Tal informação é chave para o analista técnico que está duvidando na importância de qualquer uma figura técnica no passado.
Para determinar a profundidade de memória não é preciso de nenhum poder de processamento especial. Para fazer isto, basta uma análise visual simples do gráfico do logaritmo de estatística V.
- Desenhamos uma linha de tendência ao longo de todos os pontos abrangidos no gráfico.
- Certificamo-nos de que a curva não é horizontal.
- Definimos os picos de curva ou área onde a função atinge seu máximo. São estes máximos a primeiro "bandeira vermelha" que avisa que o gráfico é susceptível de apresentar um ciclo.
- Definimos a coordenada X do gráfico em escala logarítmica e convertemos o número para um formulário que seja claro: comprimento do período = exp^ (comprimento do período em escala logarítmica). Assim, se analisássemos12000 dados horários do par GBPUSD e obtivéssemos o número 8.2 em escala logarítmico, o ciclo seria exp^8.2=3772 horas ou 157 dias.
- Todos os verdadeiros ciclos devem ser mantidos no mesmo período, mas com timeframe diferente como base. Por exemplo, no p.4 exploramos 12 000 dados horários do par GBPUSD e assumimos que tem um ciclo de 157 dias. Alternamos para o timeframe de quatro horas e analisamos de 12000/4=3000 dados, respectivamente. Se o ciclo de 157 tem lugar, é provável que você tenha feito um bom negócio. Caso contrário, não se desespere: você poderá encontrar ciclos de memória mais curtos.
3.4. Valores reais do expoente de Hurst para pares de moedas
Nós terminamos a descrição dos princípios básicos da teoria do análise fractal. Antes de proceder à aplicação imediata da análise RS por meio da linguagem de programação MQL5, eu achei necessário citar alguns exemplos.
A tabela a seguir mostra o valor de Hurst para 11 pares de moedas no mercado FOREX para diferentes timeframes e número de barras. Os coeficientes são calculados através da resolução da regressão por mínimos quadrados (MMQ). Como você pode ver, a maioria dos pares de moedas suportam formalmente o processo persistente, embora haja antipersistentes. Mas quão significativo é este resultado? Podemos confiar nestes números? Sobre isso falaremos mais tarde.
Tabela 1. Estudo do expoente de Hurst para 2000 barras
| Símbolo | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.559 | 0.513 | 0.567 | 0.577 |
| EURCHF | 0.520 | 0.468 | 0.457 | 0.463 | 0.522 | 0.577 |
| EURJPY | 0.574 | 0.501 | 0.527 | 0.511 | 0.546 | 0.577 |
| EURGBP | 0.553 | 0.571 | 0.540 | 0.562 | 0.550 | 0.577 |
| EURRUB | sem suficientes barras | 0.536 | 0.521 | 0.543 | 0.476 | 0.577 |
| USDJPY | 0.591 | 0.563 | 0.583 | 0.519 | 0.565 | 0.577 |
| USDCHF | sem suficientes barras | 0.509 | 0.564 | 0.517 | 0.545 | 0.577 |
| USDCAD | 0.549 | 0.569 | 0.540 | 0.519 | 0.565 | 0.577 |
| USDRUB | 0.582 | 0.509 | 0.564 | 0.527 | 0.540 | 0.577 |
| AUDCHF | 0.522 | 0.478c | 0.504 | 0.506 | 0.509 | 0.577 |
| GBPCHF | 0.554 | 0.559 | 0.542 | 0.565 | 0.559 | 0.577 |
Tabela 2. Estudo do exponente de Hurst para 400 barras
| Símbolo | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.513 | 0.604 | 0.617 | 0.578 |
| EURCHF | 0.471 | 0.460 | 0.522 | 0.603 | 0.533 | 0.578 |
| EURJPY | 0.545 | 0.494 | 0.562 | 0.556 | 0.570 | 0.578 |
| EURGBP | 0.620 | 0.589 | 0.601 | 0.597 | 0.635 | 0.578 |
| EURRUB | 0.580 | 0.551 | 0.478 | 0.526 | 0.542 | 0.578 |
| USDJPY | 0.601 | 0.610 | 0.568 | 0.583 | 0.593 | 0.578 |
| USDCHF | 0.505 | 0.555 | 0.501 | 0.585 | 0.650 | 0.578 |
| USDCAD | 0.590 | 0.537 | 0.590 | 0.587 | 0.631 | 0.578 |
| USDRUB | 0.563 | 0.483 | 0.465 | 0.531 | 0.502 | 0.578 |
| AUDCHF | 0.443 | 0.472 | 0.505 | 0.530 | 0.539 | 0.578 |
| GBPCHF | 0.568 | 0.582 | 0.616 | 0.615 | 0.636 | 0.578 |
Tabela 3. Resultados de cálculo do exponente de Hurst para timeframes 15M e 5M
| Símbolo | H (15M) | Importância | H (5M) | Importância | E(H) |
|---|---|---|---|---|---|
| EURUSD | 0.543 | não significativo | 0.542 | não significativo | 0.544 |
| EURCHF | 0.484 | significativo | 0.480 | significativo | 0.544 |
| EURJPY | 0.513 | não significativo | 0.513 | não significativo | 0.544 |
| EURGBP | 0.542 | não significativo | 0.528 | não significativo | 0.544 |
| EURRUB | 0.469 | significativo | 0.495 | significativo | 0.544 |
| USDJPY | 0.550 | não significativo | 0.525 | não significativo | 0.544 |
| USDCHF | 0.551 | não significativo | 0.525 | não significativo | 0.544 |
| USDCAD | 0.519 | não significativo | 0.550 | não significativo | 0.544 |
| USDRUB | 0.436 | significativo | 0.485 | significativo | 0.544 |
| AUDCHF | 0.518 | não significativo | 0.499 | significativo | 0.544 |
| GBPCHF | 0.533 | não significativo | 0.520 | não significativo | 0.544 |
Nos estudos de E. Peters é recomendado analisar algum timeframe básico e procurar nele uma série temporal com dependências cíclicas. Em seguida, recomenda-se dividir o período analisado num número de barras menor alterando o timeframe e ajustar as profundidades do histórico. Isto implica o seguinte:
Se o ciclo está presente no timeframe base, sua autenticidade é susceptível de ser comprovada no caso em que o mesmo ciclo seja encontrado numa partição diferente.
Usando diferentes combinações para o estudo das barras disponíveis, você pode encontrar ciclos não periódicos cujo comprimento será muito útil para qualquer trader que duvide da utilidade dos sinais anteriores de indicadores técnicos.
4 Da teoria à prática
Bem, neste ponto, temos um conhecimento básico sobre a análise fractal, aprendemos de que se trata o coeficiente de Hurst e como interpretar seu significado. Agora, na ordem do dia, a questão sobre ideias de programação informática usando os recursos da linguagem MQL5.
Formulamos a tarefa técnica assim: é necessário compor um programa que calcule - segundo o par de moedas definido - o coeficiente de Hurst para 1 000 barras do histórico.
Passo 1. Criamos um novo script
Como resultado obtemos um "esqueleto" que vai ser enchido com informações. Imediatamente adicionamos a propriedade #property script_show_inputs, uma vez que será necessário selecionar um par de moedas na abertura de posição.
//| New.mq5 |
//| Copyright 2016, Piskarev D.M. |
//| piskarev.dmitry25@gmail.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Piskarev D.M."
#property link "piskarev.dmitry25@gmail.com"
#property version "1.00"
#property script_show_inputs
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
//---
}
//+------------------------------------------------------------------+
Passo 2. Definimos uma matriz de preços de fechamento e, ao mesmo tempo, verificamos se atualmente estão disponíveis as 1001 barra segundo o histórico selecionado.
Por que 1001, embora T3 é definido como 1000 barras? Resposta: porque será criada uma matriz de retornos logarítmicos cuja formação precisa dos dados do valor anterior.
int copied=CopyClose(symbol,timeframe,0,barscount1+1,close); //copiamos os preços de fechamento do par selecionado na
//matriz close[]
ArrayResize(close,1001); //definimos o tamanho para a matriz
ArraySetAsSeries(close,true);
if(bars<1001) //criamos a condição de presença de 1001 barras de histórico
{
Comment("Too few bars are available! Try another timeframe.");
Sleep(10000); //atraso de registro dentro de 10 segundos
Comment("");
return;
}
Passo 3. Criamos uma matriz de retornos logarítmicos.
Entende-se que a matriz LogReturns já foi declarada e existe uma cadeia ArrayResize(LogReturns,1001)
LogReturns[i]=MathLog(close[i-1]/close[i]);
Passo 4. Calculamos o coeficiente de Hurst.
Assim, para uma análise correta, é necessário dividir o número de barras a ser examinado em subgrupos para que o número de elementos em cada um deles seja pelo menos de 10. Ou seja, nossa tarefa é encontrar divisores de 1000 cujo valor ultrapasse dez. Essas divisores são 11:
num1=10;
num2=20;
num3=25;
num4=40;
num5=50;
num6=100;
num7=125;
num8=200;
num9=250;
num10=500;
num11=1000;
Como vamos calcular os dados para a estatística RS 11 vezes, devemos escrever apropriadamente a função personalizada para esta finalidade. Os parâmetros da função serão o índice final e inicial do subgrupo - para o qual é calculada estatística RS - bem como o número de barras a serem testadas. O algoritmo dado aqui é completamente semelhante ao algoritmo que foi descrito no início.
//| Função de cálculo R/S |
//+----------------------------------------------------------------------+
double RSculc(int bottom,int top,int barscount)
{
Sum=0.0; //Valor inicial da soma igual a zero
DevSum=0.0; //Valor inicial da soma de
//desvios acumulados igual a zero
//--- Cálculo da soma de retornos
for(int i=bottom; i<=top; i++)
Sum=Sum+LogReturns[i]; //Acumulação da soma
//--- Cálculo da média
M=Sum/barscount;
//--- Cálculo de desvios acumulados
for(int i=bottom; i<=top; i++)
{
DevAccum[i]=LogReturns[i]-M+DevAccum[i-1];
StdDevMas[i]=MathPow((LogReturns[i]-M),2);
DevSum=DevSum+StdDevMas[i]; //Componente para cálculo do desvio
if(DevAccum[i]>MaxValue) //Se o valor na matriz é inferior a um certo
MaxValue=DevAccum[i]; //máximo, atribuímos ao valor máximo
//o valor do elemento da matriz DevAccum
if(DevAccum[i]<MinValue) //Lógica idêntica
MinValue=DevAccum[i];
}
//--- Cálculo da magnitude R e desvio S
R=MaxValue-MinValue; //Magnitude igual a diferença do máximo e
MaxValue=0.0; MinValue=1000; //o valor mínimo
S1=MathSqrt(DevSum/barscount); //Cálculo do desvio padrão
//--- Cálculo do indicador R/S
if(S1!=0)RS=R/S1; //Excluímos o erro divisão por "zero"
// else Alert("Zero divide!");
return(RS); //Retornamos o valor da estatística RS
}
Realizamos o cálculo usando o par switch-case.
for(int A=1; A<=11; A++) //ciclo permite tornar o código mais compacto
{ //além disso, levamos em conta todos os possíveis divisores
switch(A)
{
case 1: // 100 grupos de 10 elementos em cada
{
ArrayResize(rs1,101);
RSsum=0.0;
for(int j=1; j<=100; j++)
{
rs1[j]=RSculc(10*j-9,10*j,10); //chamamos a função personalizada RScuclc
RSsum=RSsum+rs1[j];
}
RS1=RSsum/100;
LogRS1=MathLog(RS1);
}
break;
case 2: // 50 grupos de 20 elementos em cada
{
ArrayResize(rs2,51);
RSsum=0.0;
for(int j=1; j<=50; j++)
{
rs2[j]=RSculc(20*j-19,20*j,20); //chamamos a função RScuclc
RSsum=RSsum+rs2[j];
}
RS2=RSsum/50;
LogRS2=MathLog(RS2);
}
break;
...
...
...
case 9: // 125 and 16 groups
{
ArrayResize(rs9,5);
RSsum=0.0;
for(int j=1; j<=4; j++)
{
rs9[j]=RSculc(250*j-249,250*j,250);
RSsum=RSsum+rs9[j];
}
RS9=RSsum/4;
LogRS9=MathLog(RS9);
}
break;
case 10: // 125 and 16 groups
{
ArrayResize(rs10,3);
RSsum=0.0;
for(int j=1; j<=2; j++)
{
rs10[j]=RSculc(500*j-499,500*j,500);
RSsum=RSsum+rs10[j];
}
RS10=RSsum/2;
LogRS10=MathLog(RS10);
}
break;
case 11: //200 and 10 groups
{
RS11=RSculc(1,1000,1000);
LogRS11=MathLog(RS11);
}
break;
}
}
Passo 5. Função personalizada de cálculo da regressão linear por mínimos quadrados (MMQ).
Os parâmetros de entrada são os valores dos componentes calculados da estatística RS.
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6,
double Y7,double Y8,double Y9,double Y10,double Y11)
{
double SumY=0.0;
double SumX=0.0;
double SumYX=0.0;
double SumXX=0.0;
double b=0.0;
double N[]; //matriz na qual serão localizados os algoritmos dos divisores
double n={10,20,25,40,50,100,125,200,250,500,1000} //matriz de divisores
//---Cálculo de coeficientes N
for (int i=0; i<=10; i++)
{
N[i]=MathLog(n[i]);
SumX=SumX+N[i];
SumXX=SumXX+N[i]*N[i];
}
SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11;
SumYX=Y1*N1+Y2*N2+Y3*N3+Y4*N4+Y5*N5+Y6*N6+Y7*N7+Y8*N8+Y9*N9+Y10*N10+Y11*N11;
//---Cálculo do coeficiente Beta da regressão ou o exponente de Hurst desejado
b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX);
return(b);
}
Passo 6. Função personalizada para cálculo dos valores esperados da estatística RS. A lógica de cálculo é explicada na parte teórica.
//| Função de cálculo de valores esperados E(R/S) |
//+----------------------------------------------------------------------+
double ERSculc(double m) //m - divisor 1000
{
double e;
double nSum=0.0;
double part=0.0;
for(int i=1; i<=m-1; i++)
{
part=MathPow(((m-i)/i), 0.5);
nSum=nSum+part;
}
e=MathPow((m*pi/2),-0.5)*nSum;
return(e);
}
Em última análise, o código completo do programa pode ficar da seguinte maneira:
//| hurst_exponent.mq5 |
//| Copyright 2016, Piskarev D.M. |
//| piskarev.dmitry25@gmail.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Piskarev D.M."
#property link "piskarev.dmitry25@gmail.com"
#property version "1.00"
#property script_show_inputs
#property strict
input string symbol="EURUSD"; // Symbol
input ENUM_TIMEFRAMES timeframe=PERIOD_D1; // Timeframe
double LogReturns[],N[],
R,S1,DevAccum[],StdDevMas[];
int num1,num2,num3,num4,num5,num6,num7,num8,num9,num10,num11;
double pi=3.14159265358979323846264338;
double MaxValue=0.0,MinValue=1000.0;
double DevSum,Sum,M,RS,RSsum,Dconv;
double RS1,RS2,RS3,RS4,RS5,RS6,RS7,RS8,RS9,RS10,RS11,
LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,LogRS9,
LogRS10,LogRS11;
double rs1[],rs2[],rs3[],rs4[],rs5[],rs6[],rs7[],rs8[],rs9[],rs10[],rs11[];
double E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11;
double H,betaE;
int bars=Bars(symbol,timeframe);
double D,StandDev;
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
double close[]; //Declaramos a matriz dinâmica de preços de fechamento
int copied=CopyClose(symbol,timeframe,0,1001,close); //Copiamos os preços de fechamento do par selecionado na
//matriz close[]
ArrayResize(close,1001); //Atribuímos o tamanho da matriz
ArraySetAsSeries(close,true);
if(bars<1001) //Criamos a condição de presença de 1001 barras de histórico
{
Comment("Too few bars are available! Try another timeframe.");
Sleep(10000); //Atraso de registro de 10 segundos
Comment("");
return;
}
//+------------------------------------------------------------------+
//| Preparação de matrizes |
//+------------------------------------------------------------------+
ArrayResize(LogReturns,1001);
ArrayResize(DevAccum,1001);
ArrayResize(StdDevMas,1001);
//+------------------------------------------------------------------+
//| Matriz de retornos logarítmicos |
//+------------------------------------------------------------------+
for(int i=1;i<=1000;i++)
LogReturns[i]=MathLog(close[i-1]/close[i]);
//+------------------------------------------------------------------+
//| |
//| análise R/S |
//| |
//+------------------------------------------------------------------+
//--- Definimos o número de elementos em cada subgrupo
num1=10;
num2=20;
num3=25;
num4=40;
num5=50;
num6=100;
num7=125;
num8=200;
num9=250;
num10=500;
num11=1000;
//--- Cálculo de compostos Log(R/S)
for(int A=1; A<=11; A++)
{
switch(A)
{
case 1:
{
ArrayResize(rs1,101);
RSsum=0.0;
for(int j=1; j<=100; j++)
{
rs1[j]=RSculc(10*j-9,10*j,10);
RSsum=RSsum+rs1[j];
}
RS1=RSsum/100;
LogRS1=MathLog(RS1);
}
break;
case 2:
{
ArrayResize(rs2,51);
RSsum=0.0;
for(int j=1; j<=50; j++)
{
rs2[j]=RSculc(20*j-19,20*j,20);
RSsum=RSsum+rs2[j];
}
RS2=RSsum/50;
LogRS2=MathLog(RS2);
}
break;
case 3:
{
ArrayResize(rs3,41);
RSsum=0.0;
for(int j=1; j<=40; j++)
{
rs3[j]=RSculc(25*j-24,25*j,25);
RSsum=RSsum+rs3[j];
}
RS3=RSsum/40;
LogRS3=MathLog(RS3);
}
break;
case 4:
{
ArrayResize(rs4,26);
RSsum=0.0;
for(int j=1; j<=25; j++)
{
rs4[j]=RSculc(40*j-39,40*j,40);
RSsum=RSsum+rs4[j];
}
RS4=RSsum/25;
LogRS4=MathLog(RS4);
}
break;
case 5:
{
ArrayResize(rs5,21);
RSsum=0.0;
for(int j=1; j<=20; j++)
{
rs5[j]=RSculc(50*j-49,50*j,50);
RSsum=RSsum+rs5[j];
}
RS5=RSsum/20;
LogRS5=MathLog(RS5);
}
break;
case 6:
{
ArrayResize(rs6,11);
RSsum=0.0;
for(int j=1; j<=10; j++)
{
rs6[j]=RSculc(100*j-99,100*j,100);
RSsum=RSsum+rs6[j];
}
RS6=RSsum/10;
LogRS6=MathLog(RS6);
}
break;
case 7:
{
ArrayResize(rs7,9);
RSsum=0.0;
for(int j=1; j<=8; j++)
{
rs7[j]=RSculc(125*j-124,125*j,125);
RSsum=RSsum+rs7[j];
}
RS7=RSsum/8;
LogRS7=MathLog(RS7);
}
break;
case 8:
{
ArrayResize(rs8,6);
RSsum=0.0;
for(int j=1; j<=5; j++)
{
rs8[j]=RSculc(200*j-199,200*j,200);
RSsum=RSsum+rs8[j];
}
RS8=RSsum/5;
LogRS8=MathLog(RS8);
}
break;
case 9:
{
ArrayResize(rs9,5);
RSsum=0.0;
for(int j=1; j<=4; j++)
{
rs9[j]=RSculc(250*j-249,250*j,250);
RSsum=RSsum+rs9[j];
}
RS9=RSsum/4;
LogRS9=MathLog(RS9);
}
break;
case 10:
{
ArrayResize(rs10,3);
RSsum=0.0;
for(int j=1; j<=2; j++)
{
rs10[j]=RSculc(500*j-499,500*j,500);
RSsum=RSsum+rs10[j];
}
RS10=RSsum/2;
LogRS10=MathLog(RS10);
}
break;
case 11:
{
RS11=RSculc(1,1000,1000);
LogRS11=MathLog(RS11);
}
break;
}
}
//+----------------------------------------------------------------------+
//| Cálculo do coeficiente de Hurst |
//+----------------------------------------------------------------------+
H=RegCulc1000(LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,
LogRS9,LogRS10,LogRS11);
//+----------------------------------------------------------------------+
//| Cálculo de valores esperados log(E(R/S)) |
//+----------------------------------------------------------------------+
E1=MathLog(ERSculc(num1));
E2=MathLog(ERSculc(num2));
E3=MathLog(ERSculc(num3));
E4=MathLog(ERSculc(num4));
E5=MathLog(ERSculc(num5));
E6=MathLog(ERSculc(num6));
E7=MathLog(ERSculc(num7));
E8=MathLog(ERSculc(num8));
E9=MathLog(ERSculc(num9));
E10=MathLog(ERSculc(num10));
E11=MathLog(ERSculc(num11));
//+----------------------------------------------------------------------+
//| Cálculo de beta dos valores esperados E(R/S) |
//+----------------------------------------------------------------------+
betaE=RegCulc1000(E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11);
Alert("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3));
Comment("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3));
}
//+----------------------------------------------------------------------+
//| Função de cálculo R/S |
//+----------------------------------------------------------------------+
double RSculc(int bottom,int top,int barscount)
{
Sum=0.0; //Valor inicial da soma igual a zero
DevSum=0.0; //Valor inicial da soma de
//desvios acumulados igual a zero
//--- Cálculo de soma de retornos
for(int i=bottom; i<=top; i++)
Sum=Sum+LogReturns[i]; //Acumulação da soma
//--- Cálculo de média
M=Sum/barscount;
//--- Cálculo de desvios acumulados
for(int i=bottom; i<=top; i++)
{
DevAccum[i]=LogReturns[i]-M+DevAccum[i-1];
StdDevMas[i]=MathPow((LogReturns[i]-M),2);
DevSum=DevSum+StdDevMas[i]; //Componente para o cálculo do desvio
if(DevAccum[i]>MaxValue) //Se o valor na matriz é inferior a um certo
MaxValue=DevAccum[i]; //máximo, atribuímos ao valor máximo
//valor do elemento da matriz DevAccum
if(DevAccum[i]<MinValue) //Lógica idêntica
MinValue=DevAccum[i];
}
//--- Cálculo da magnitude R e do desvio S
R=MaxValue-MinValue; //Magnitude igual a diferença do máximo e
MaxValue=0.0; MinValue=1000; //valor mínimo
S1=MathSqrt(DevSum/barscount); //Cálculo do desvio padrão
//--- Cálculo do indicador R/S
if(S1!=0)RS=R/S1; //Excluímos o erro de divisão por "zero"
// else Alert("Zero divide!");
return(RS); //Retornamos o valor da estatística RS
}
//+----------------------------------------------------------------------+
//| Calculadora de regressão |
//+----------------------------------------------------------------------+
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6,
double Y7,double Y8,double Y9,double Y10,double Y11)
{
double SumY=0.0;
double SumX=0.0;
double SumYX=0.0;
double SumXX=0.0;
double b=0.0; //matriz na qual serão localizados os algoritmos dos divisores
double n[]={10,20,25,40,50,100,125,200,250,500,1000}; //matriz de divisores
//---Cálculo de coeficientes N
ArrayResize(N,11);
for (int i=0; i<=10; i++)
{
N[i]=MathLog(n[i]);
SumX=SumX+N[i];
SumXX=SumXX+N[i]*N[i];
}
SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11;
SumYX=Y1*N[0]+Y2*N[1]+Y3*N[2]+Y4*N[3]+Y5*N[4]+Y6*N[5]+Y7*N[6]+Y8*N[7]+Y9*N[8]+Y10*N[9]+Y11*N[10];
//---Cálculo do coeficiente Beta da regressão ou do exponente de Hurst desejado
b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX);
return(b);
}
//+----------------------------------------------------------------------+
//| Função de cálculo de valores esperados E(R/S) |
//+----------------------------------------------------------------------+
double ERSculc(double m) //m - divisor 1000
{
double e;
double nSum=0.0;
double part=0.0;
for(int i=1; i<=m-1; i++)
{
part=MathPow(((m-i)/i), 0.5);
nSum=nSum+part;
}
e=MathPow((m*pi/2),-0.5)*nSum;
return(e);
}
Claro, se quiser, você pode atualizar o código para implementar nele uma ampla gama de recursos de cálculo e criar uma interface gráfica fácil de usar.
No capítulo final, vamos falar sobre as soluções de software existentes.
5. Soluções de software
Há muitos recursos de software nos quais já é implementado o algoritmo de análise R/S. Normalmente, no entanto, a implementação deste algoritmo é comprimida e deixa a maior parte do trabalho analítico ao usuário. O pacote Matlab tem a ver com esses exemplos.
Há também um utilitário para o terminal MetaTrader 5 disponível no Mercado chamado de Fractal Analysis, com sua ajuda o usuário pode realizar a análise fractal dos mercados financeiros. Vamos entender como trabalhar com este analisador.
5.1. Selecione uma estrela
Na verdade, embora haja muitos parâmetro, nós apena estaremos interessados nos três primeiros, ou seja, Symbol, Number of bars e Timeframe.
Na captura de tela abaixo podemos ver como a Fractal Analysis permite selecionar um par de moedas, inclusive não importa se o utilitário é executado na janela de cada instrumento, uma vez que o mais importante é especificar o símbolo na janela inicialização.
Selecionamos o número de barras do timeframe definido.
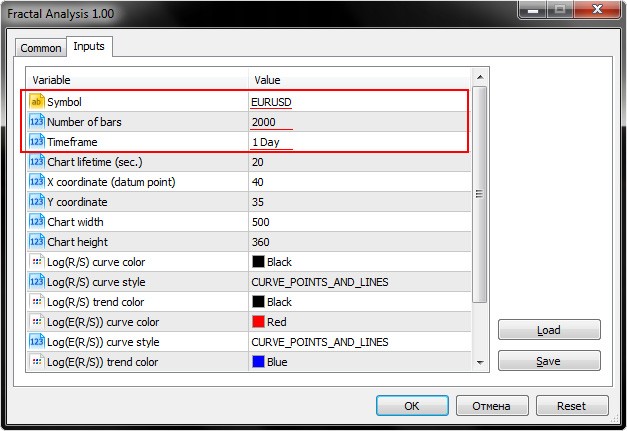
Repare em que o parâmetro Chart lifetime define o número de segundos durante os quais você pode trabalhar com o utilitário. Como resultado, após pressionar o botão "OK", o analisador aparece no canto superior esquerdo da janela principal do terminal MetaTrader 5. Um exemplo é mostrado na imagem abaixo.
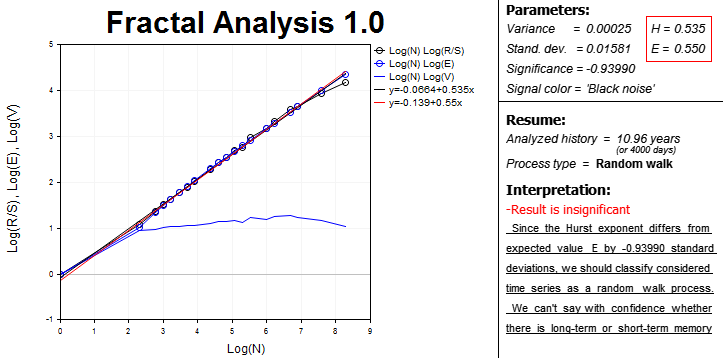
Em última análise, na tela aparecerão todos os dados e resultados necessários para análise fractal.
Na parte esquerda, é apresentada a área com dependências gráficas numa escala logarítmica:
- Estatísticas R/S a partir do número de observações na amostragem;
- valor esperado de estatística R/S de E(R/S) a partir do número de observações;
- estatísticas V a partir do número de observações.
Esta é uma área interativa que envolve o uso de ferramentas MetaTrader 5 para análise de gráficos, uma vez que por vezes é bastante difícil encontrar o comprimento do ciclo "a olho".
Também são apresentadas as equações de curvas e linhas de tendência, cuja inclinação é usada para determinar os exponentes numéricos de Hurst (H). Além disso, é calculado o valor esperado do expoente de Hurst (E). No bloco adjacente à direita, além de se encontrarem estas equações, são calculados a dispersão, a significância da análise e o espectro de cores do sinal.
Para a conveniência do usuário, o programa calcula em dias o comprimento do período de estudo. Isto deve ser entendido para avaliar a significância dos dados históricos.
Na cadeia de caracteres Process type é exibida a caraterística da série temporal:
- persistente;
- antipersistente;
- passeio aleatório.
E finalmente, no bloco "Interpretation", é exibido um breve resumo que será útil para o analista que tem pouca experiência com a análise fractal.
5.2. Exemplo de trabalho
Definimos quais são o instrumento e o intervalo que vamos analisar. Pegamos o par "dólar neozelandês e franco suíço" (NZDCHF) e olhamos para as últimas cotações na escala de tempo (H1).
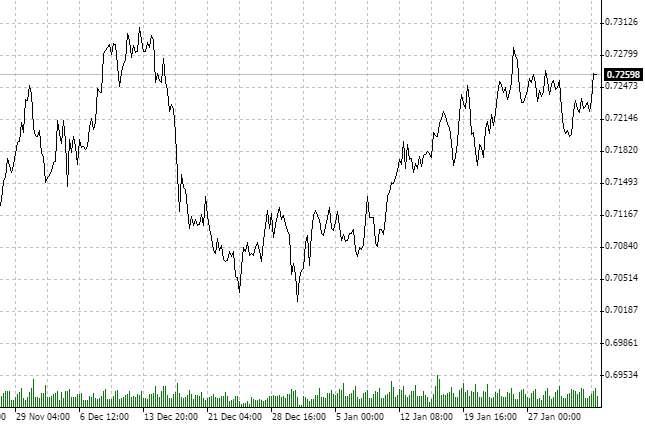
Note que mais o menos nos últimos dois meses o mercado tem estado em modo de consolidação. Novamente, NÃO estamos interessados em outros horizontes de investimento. É bem possível que o gráfico diário mostre uma tendência ascendente ou descendente. Nós selecionamos 1H e certo número de dados históricos.
Aparentemente, o processo é antipersistente. Vamos verificar isto usando a Fractal Analysis.
De 21.11 a 3.02 nós temos um histórico de 75 dias. Mudamos 75 dias para horas. Obtemos 1800 dados horários. Como na entrada do utilitário não há tal número de barras, definimos o valor mais próximo, isto é, 2000 períodos horários analisados.
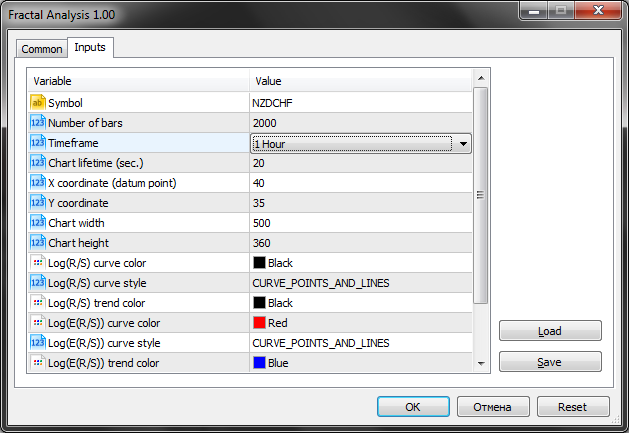
Como resultado, obtemos a seguinte imagem:
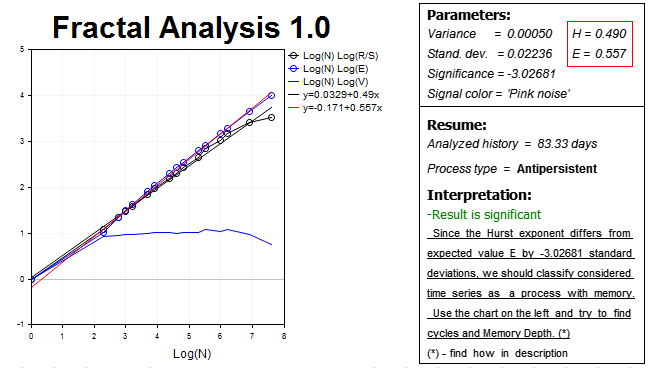
Como você pode ver, nossa hipótese é confirmada, quer dizer, neste horizonte o mercado monstra um processo antipersistente, inclusive bastante significativo, uma vez que o valor do exponente de Hurst H=0.490, isto é, praticamente três desvios-padrão abaixo do valor esperado E=0.557.
Fixamos o resultado e pegamos um timeframe um pouco superior (H2) e, por conseguinte, duas vezes menos barras do histórico — 1000 valores. O resultado será o seguinte:
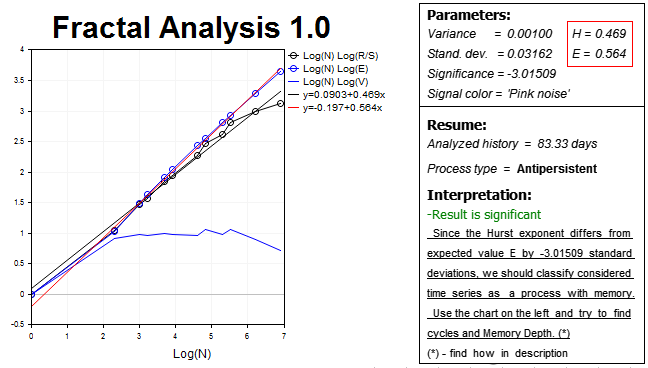
Mais uma vez vemos antipersistência. O exponente de Hurst H=0.469 fica atrasado - num número superior a três desvios-padrão - em relação ao valor esperado do coeficiente E=0.564.
Agora tentamos encontrar ciclos.
Voltamos para o gráfico para H1 e tentamos capturar o momento em que a curva R/S se separa de E(R/S). Este momento é caracterizado pela formação de um pico no gráfico de estatísticas V. Assim, agora podemos determinar o valor aproximado do ciclo.
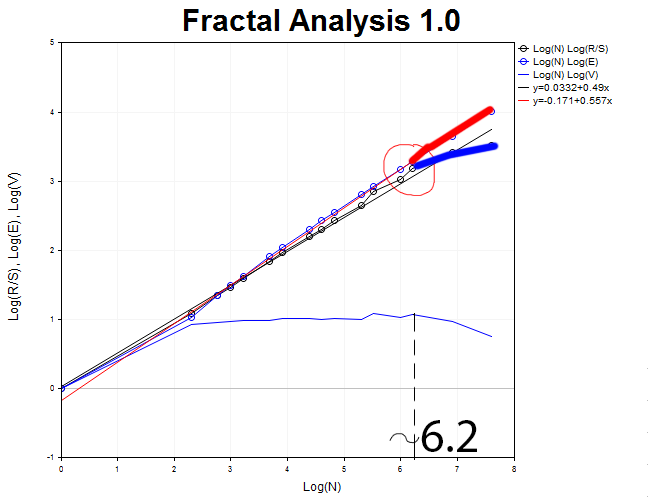
Ele é aproximadamente igual a N1 = 2.71828^6.2 = 493 horas, o que equivale a 21 dias.
Claro, não se deve falar com certeza sobre a confiabilidade do resultado quando temos os resultados apenas de um experimento. Como mencionado acima, é necessário "jogar" com os timeframes e tentar selecionar todas as combinações possíveis "timeframe — número de barras", a fim de ter a certeza da validez do resultado obtido.
Realizamos a análise gráfica de 1000 barras do timeframe H2.
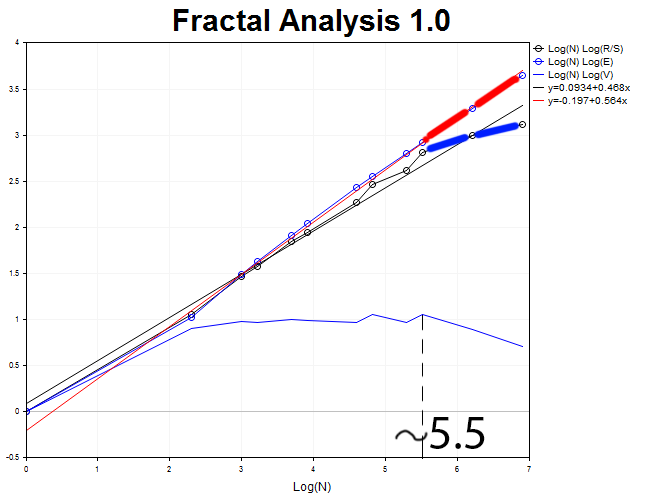
O comprimento do ciclo é igual a N2 = 2.71828^5.5 = 245 períodos de duas horas, o que é aproximadamente equivalente a vinte dias.
Analisemos agora o timeframe de 30 minutos e 4000 valores. Obtemos o processo antipersistente com um exponente de Hurst H = 0.492 e valor esperado E=0.55, que ultrapassa H em 3,6 desvios-padrão.
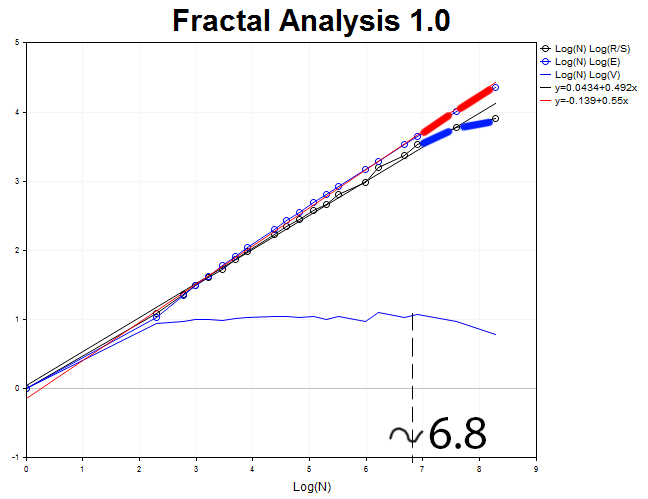
Comprimento do ciclo N3 = 2.71828^6.8 = 898 de trechos de trinta minutos ou 18.7 dias.
Como um exemplo de aprendizagem bastarão três testes. Encontramos o valor médio das comprimentos obtidos do período M= (N1 + N2 + N3)/3 = (21 + 20 + 18.7)/3 = 19.9 ou 20 dias.
Como resultado, nós obtemos um período em cujos limites é realmente possível confiar e nos quais está baseada a estratégia de negociação. Mais uma vez, repito que este cálculo e análise são ilustrados aqui para um horizonte de investimento de dois meses de duração. Isto significa que a análise perde sua relevância ao alternar para a negociação intradia, uma vez que, nela, é possível que ocorram seus processos cíclicos de curtíssimo prazo, cuja presença ou ausência deve ser provada. Se não forem encontrados os ciclos, não só a análise técnica perderá relevância e eficácia, mas também a solução razoável passará para a implementação da negociação usando notícias e a "negociação baseada em sentimentos" (no sentimento do mercado).
Conclusão
A analise fractal é uma espécie de sinergia entre as abordagens fundamental e estatística à previsão dinâmica do mercado. É um método de processamento de informação versátil, uma vez que a análise R/S e o exponente de Hurst se provaram com sucesso em áreas da ciência como a geografia, biologia, física, economia. A análise fractal pode ser usada para construir modelos de pontuação ou avaliação implementados por instituições de crédito a fim de analisar a solvência dos mutuários.
E para concluir, gostaria de repetir a ideia contida no início do artigo: para negociar com sucesso no mercado Forex, é sempre importante saber um pouco mais do que os outros traders. Como antecipo uma errada compreensão da informação apresentada, quero advertir o leitor de que o mercado tende a "enganar" o analista. Por isso, sempre verifique a existência de um ciclo não periódico nos timeframes superiores e inferiores. Se ele não aparecer noutros timeframes, o ciclo será provavelmente ruído do mercado.